基于隨機矩陣理論和改進粒子群優化-深度置信網絡的無功優化

夏 芃，張 倩，王群京，王 璨

(1.安徽大學電氣工程及自動化學院，合肥 230601；2.安徽大學工業節電與電能質量控制協同創新中心，合肥 230601;3.教育部電能質量工程研究中心(安徽大學)，合肥 230601；4.工業節電與用電安全安徽省重點實驗室(安徽大學)，合肥 230601；5.國網安徽省電力有限公司，合肥 230601)

分布式電源并網導致配電網結構趨于復雜，配電網電壓波動過大[1]、網損較大[2]等問題日趨嚴重。因此，如何保障電力系統穩定且安全運行，并減小配電網電壓波動和網損是國內外學者研究的熱點。配電網無功優化是指在電力系統能穩定且安全運行的前提情況下通過針對配電網發電機端電壓的調節[3]、變壓器分接頭次數[4]以及增加無功補償裝置[5-6]等方式來減少電壓波動并降低網損。

為解決大規模分布式電源并網所引發的相關問題，目前中外學者主要從改變無功優化模型以及無功優化算法等方面進行研究。文獻[7]通過建立系統運行成本和用戶滿意度為目標的配電網無功優化模型，提高了計算精度和速度。文獻[8]建立了混合整數半定規劃模型，先將傳統無功優化模型轉化成半定規劃模型，在此基礎上增加離散變量使其變成混合整數半定規劃模型，使配電網無功優化模型的求解更加方便。上述改進雖然和配電網原始模型相比計算速度得到提高，但改進的方法過于依賴配電網的模型，當配電網的模型過于復雜時，該方法存在局限性。文獻[9]將禁忌搜索算法和粒子群算法相融合，對傳統的粒子群算法進行改進，并運用到配電網無功優化策略當中。文獻[10]通過構造初始信息矩陣和蟻群算法相結合，提高了蟻群算法的計算效率，上述算法改進雖然和傳統算法相比尋優精度和計算精度有所提高，但仍未擺脫算法計算時間長、步驟較為復雜的特點。

近些年來，大數據技術在電力系統中的應用越來越廣泛，從而給配電網無功優化的方法帶來了一種新的途徑。目前大數據技術大多用于電力系統負荷預測以及故障診斷領域[11-13]，但是部分學者也將大數據技術和配電網無功優化應用領域相結合。文獻[14]運用大數據技術對風力發電廠并入光伏后的電壓進行無功控制。文獻[15]將支持向量機的方法運用到遺傳算法當中并加以改進，得出了基于數據挖掘技術的無功優化策略。文獻[16]將負荷分布匹配與熵權理論相結合，運用熵權法從歷史優化方案中選擇最優無功優化控制方案。文獻[17]將粒子群算法對極限學習機進行優化，并運用到配電網的調壓策略中。上述基于數據挖掘技術的無功優化控制策略對配電網具體模型依賴程度低，均取得了較好的無功優化控制效果。

配電網無功優化是典型的高維非線性函數問題，而深度學習理論可直接確定輸入和輸出之間的隱含關系。其中，深度置信網絡(deep belief networks，DBN)的網絡模型結構較為簡單且訓練難度較低，常用于求解高維非線性函數問題。現利用配電網運行的光伏、負荷、溫度、光照強度以及風速5個數據構造隨機矩陣構成樣本集，運用粒子群優化 (particle swarm optimization,PSO)對DBN的初始權重進行優化，通過建立PSO-DBN模型得出配電網運行特征與無功優化策略的函數關系，將本文方法用于改進后的IEEE33節點，并和粒子群優化方法、改進的粒子群優化方法以及DBN對比，以驗證本文方法對電壓波動和網損的調節效果。

1 隨機矩陣理論

隨機矩陣理論[18]是一種常用的大數據分析方法，其主要應用于故障診斷以及變電站二次評估。當隨機矩陣的行數和列數的比值保持恒定時，其經驗分布函數滿足單環定律、半圓律等。主要以單環定律進行研究。

1.1 單環定理

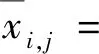
i=1,2,…,N,j=1,2,…,T

(1)

(2)

式(2)中：U為酉矩陣。

(3)

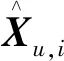
根據式(4)將矩陣積標準化得

(4)

(5)

式(5)中：λ為矩陣的特征值。

1.2 線性特征值統計量

線性特征值統計量是對隨機矩陣特征值分布的特點具體形式的表現,而線性特征值統計量定義為

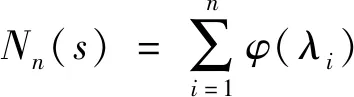
(6)

式(6)中：s為統計函數對應的映射值；λi(i=1,2,…,n)為隨機矩陣的特征值；φ(·)為一個線性特征統計函數，不同的線性統計函數的選擇即可得到不同的線性特征統計量。

1.3 特征指標的提取

采用光伏、負荷、溫度、環境以及風速共5種數據，每種數據用單環定理算出隨機矩陣的特征值，然后通過特征值計算每種隨機矩陣的平均譜半徑、最大/最小譜半徑、圓環外/上/內特征根的分布概況。隨機矩陣的模以及協方差共8個統計特征，因而5種數據共構成40種統計特征。每個統計特征的具體公式為

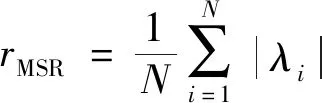
(7)

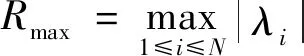
(8)

(9)

(10)

(11)

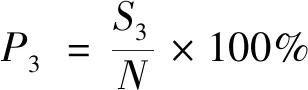
(12)

式中：N為矩陣特征值的個數；rMSR、Rmax、Rmin分別為平均譜半徑、最大以及最小譜半徑；P1、P2、P3分別為圓環外/上/內的特征值占總特征值比例；S1、S2、S3分別為分布在圓環外、上、內的特征值個數。

(13)

(14)

2 DBN理論

DBN由多層受限玻爾茲曼機(restricted Boltzmann machine,RBM)和最外層的BP網絡構造而成[19]，具體結構如圖1所示。

圖1 DBN結構Fig.1 DBN structure

DBN的訓練步驟主要有RBM的預訓練以及DBN參數反向微調。預訓練即通過輸入自下而上逐層訓練RBM，如此進行反復訓練，不斷優化網絡中的模型參數，使網絡達到局部最優。而參數的反向微調即以DBN模型的最后一層為輸入，運用BP神經網絡自下而上地微調整個DBN的網絡模型參數，從而實現全局參數最優。

2.1 RBM預訓練

RBM作為概率神經網絡的分支，主要由可視層以及隱藏層所構成的。可視層v=(v1,v2,…,vm)以及隱含層h=(h1,h2,…,hn)的聯合概率能量函數為

(15)

式(15)中：θ={ω,a,b}為RBM網絡模型相關參數；vi和ai分別為可視層神經元的當前狀態以及該層網絡的偏置；hj和bj分別為隱含層神經元的當前狀態以及偏置；ωij為每層之間所需連接的權值。

在RBM中定義任意一組關于v和h的聯合概率分布為

(16)

而由聯合概率分布可得v和h的條件分布為

(17)

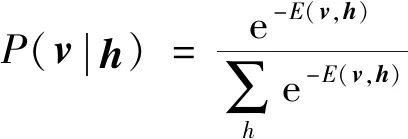
(18)

RBM的訓練的最終目的即找到合適的參數θ={ω,a,b}，進而使RBM的能量誤差函數達到最小值。

2.2 DBN的反向微調

當每層的RBM參數調整完成之后，卻很難保證整體DBN的參數達到最佳。因此，需要運用BP算法針對整個DBN網絡參數進行微調，具體微調過程是利用反向誤差將權值進行更新，因而獲得了整體DBN的最佳網絡參數。

在參數調整過程當中，將RBM訓練的最后一層作為輸入，利用BP算法對RBM預訓練過程中產生的訓練誤差自下而上傳到RBM層中，進而調節整個DBN網絡，大大減少了訓練時間。反向微調過程中參數更新公式為

(19)

式(19)中：ωn為每層網絡之間的權值；n為RBM更新迭代次數；η為學習率；m為動量系數。

3 基于PSO-DBN無功優化策略

3.1 粒子群優化算法及其改進

在建立DBN模型之初，DBN網絡初始權重是通過隨機賦值所得出，若賦值不恰當會使得DBN模型在訓練中會出現局部收斂現象,因而采用粒子群算法對DBN網絡初始權重進行優化。

粒子群優化算法作為一種啟發式算法，其算法本身是通過對每個粒子的速度Vi和位置Xi進行更新，當滿足結束條件時，即可獲得最優解，粒子的速度以及位置更新公式為

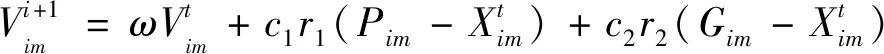
(20)

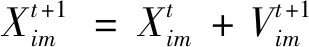
(21)

式中：m=1,2,…,M；ω為粒子的權值；c1和c2為學習因子；r1和r2為在0～1所取的隨機數；t為迭代次數；Pim和Gim為個體以及群體極值。

因為傳統的粒子群算法易陷入局部最優解的狀況。因此，對其改進的方法也有很多。目前大多數學者主要采用調整權重、限制學習因子等方法對粒子群算法進行改進。

主要使用對慣性權重的改進，通過線性權重遞減法，具體公式為

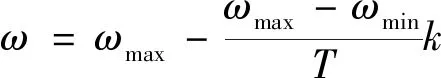
(22)

式(22)中：ωmax、ωmin分別為粒子群算法初始權重的最大值以及最小值；T為最高迭代次數；k為當前迭代次數。

3.2 PSO優化DBN網絡的無功優化策略

基于PSO-DBN網絡的無功優化流程圖如圖2所示，其具體優化步驟如下。

圖2 PSO-DBN無功優化流程圖Fig.2 PSO-DBN reactive power optimization flowchart

步驟1對配電網歷史時刻的負荷、光伏、環境、溫度以及風速分別構建各時刻的5種隨機矩陣。

步驟2根據前文所述的特征指標提取方法，提取出40個歷史特征指標集，進行歸一化處理并得到樣本訓練集和測試集。

步驟3確定DBN網絡中隱含層層數及隱含層中神經元的個數，以便對粒子維度進行確定。

步驟4對粒子群各參數進行設置，即粒子的群體規模、學習因子、慣性權重以及最大迭代次數。并將DBN網絡中各層之間的連接權值作為PSO的向量。

步驟5計算粒子的適應度函數值f。其函數為

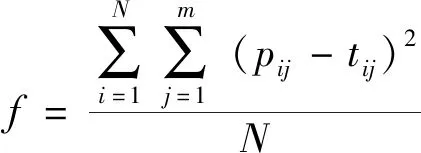
(23)

式(23)中：N為樣本數目；m為粒子維數；pij和tij分別為第i個樣本中第j維粒子的重構值和實際值。f和個體極值Pbest進行比較，若f>Pbest，則將當前適應度值替換掉,否則將個體極值保留。

步驟6將每個粒子的適應度值大小f和群體極值gbest相比較，若f>gbest，則將當前適應度值替換掉,否則將群體極值保留。

步驟7根據式(20)和式(21)將粒子的速度以及位置進行更新。

步驟8利用PSO優化后獲得的群體極值的各維數值作為DBN網絡的初始權重。再進行DBN模型的訓練和參數微調，直至DBN訓練結束，DBN的網絡模型建立，從而得到無功優化策略。

4 算例分析

4.1 算例介紹及樣本數據集的構造

以IEEE33節點系統作為研究對象，對系統的22節點和33節點增加無功補償，在16-17支路、19-20支路、24-25支路、26-27支路進行變壓器分接頭變比的調節，TA1～TA4分別為4個載調壓器，SVC代表無功補償，其改進后的節點拓撲圖如圖3所示。

圖3 改進IEEE33節點拓撲結構圖Fig.3 Improved IEEE33 node topology diagram

配電網運行狀態數據源于安徽省安慶市電網公司數據集。利用配電網兩個月的負荷、光伏、環境、溫度以及風速構造5種隨機矩陣。研究每小時配電網的無功優化策略，構造5種不同的高維隨機矩陣，提取特征統計量作為歷史輸入，從當地電網數據庫中得到兩個月中每小時的無功優化控制策略作為歷史輸出，構成1 440個歷史樣本的輸入和輸出標簽,放入PSO-DBN模型中進行訓練，訓練過程中設置DBN網絡共有4層結構，兩層隱含層神經元的數量可分別設為20和10。粒子群優化算法參數設置如下：ωmax=0.9，ωmin=0.5，學習因子c1=c2=2,T=1 000。接著，選取前文所述兩個月之外的某日作為待優化時刻，利用隨機矩陣理論獲取該天每小時共24個特征統計量作為樣本輸入，再將輸入運用到訓練好的DBN模型中得到當前時刻的無功優化策略。圖4和圖5表明了該日通過本文方法得出改進后IEEE33節點系統的變壓器調節擋位和無功補償量。再將所得策略進行仿真計算。

圖4 IEEE33節點各支路變壓器檔位調節圖Fig.4 IEEE33 node branch transformer tap adjustment diagram

圖5 22節點和33節點無功補償Fig.5 Reactive compensation of22 and 33 node

4.2 無功優化結果分析

為更好地驗證本文方法在無功優化方面的有效性，將本文方法與PSO算法、改進PSO算法、DBN這3種優化方法調壓所得的電壓波動和網損進行對比，以系統降損率和系統電壓偏差波動率為指標，可更直觀地看出本文方法調壓策略的有效性。其中定義某時刻系統降損率為

(24)

式(24)中：eL為系統降損率；f0為系統該時刻未使用任何調壓方法所得的網損；f為系統該時刻使用調壓方法所得的網損。

定義某時刻的系統電壓偏差波動率為

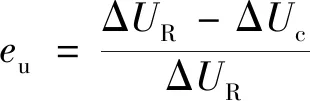
(25)

式(25)中：eu為系統電壓偏差波動率；ΔUR為系統該時刻運用調壓算法調壓所得的電壓值；ΔUc為系統該時刻未使用任何調壓方法所得的電壓值。

運用式(24)和式(25)對無功優化結果分析，對于待優化的24個時刻，4種優化方法的系統降損率如圖6和表1所示，系統電壓偏差波動率如圖7和表2所示。

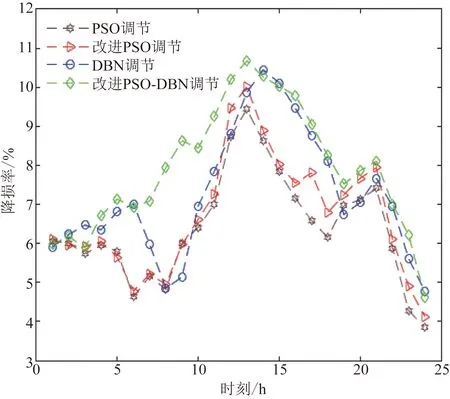
圖6 降損率比較Fig.6 Comparison of loss reduction rate curve

表1 降損率分析Table 1 Analysis of loss reduction rate

圖7 電壓偏差波動率比較Fig.7 Comparison of voltage deviation volatility rate curve

表2 電壓偏差波動率分析Table 2 Analysis of voltage deviation volatility

由圖6及表1可知，在減少網損方面，本文方法在當天的降損率曲線幅度要大于其他3種方法的曲線，而降損率均值和方差分別為7.94%和1.67%，均高于其他2種方法。由圖7及表2可知，在減小電壓波動方面，該方法的整體電壓偏差波動率曲線幅度要小于其他3種方法的曲線，而電壓偏差波動率均值和方差分別為0.94%和0.29%,均小于其他2種方法。

5 結論

針對配電網的無功優化問題,提出了基于PSO-DBN的配電網無功優化方法，并在IEEE33節點系統進行仿真實驗，得出以下結論。

(1)利用隨機矩陣理論對配電網運行狀態數據進行特征提取，大大提高了數據利用率，可有效地體現出配電網的運行狀態，為后續配電網無功優化策略的分析提供了重要數據來源。

(2)所建立的改進PSO-DBN模型可搭建配電網運行狀態與配電網無功優化策略之間的關系，使得無功優化效果得以提高。

(3)本文方法對配電網模型參數依賴程度較低，并不需要配電網的網架結構的具體參數，僅需將配電網運行狀態合無功優化策略之間建立深度學習模型，相較于傳統優化方法無功優化效果有所提高。