雷諾數和湍流度對葉片表面邊界層轉捩和換熱特性的影響

王裕東,趙長宇，李廣超*，王晶晶，張 魏

(1.沈陽航空航天大學航空發動機學院,沈陽 110136；2.西北工業大學動力與能源學院,西安 710129)

為了提高燃氣渦輪發動機的性能和效率，渦輪前溫度不斷提升，渦輪葉片工作環境愈加惡劣，要使葉片正常工作需要合理設計冷卻結構[1-2]。冷卻結構設計必須以葉片外換熱特性為依據[3-4]，發動機工作狀態變化導致葉片表面邊界層轉捩點變化，邊界層流態改變使換熱突然增強[5]，因此冷卻薄弱部位并不固定，需要詳細分析轉捩點在不同工況下的變化規律，準確預測不同工況下轉捩點變化區間。

臨界雷諾數判據只適用于無壓力梯度情況[6]，使用動量厚度雷諾數預測轉捩點可以將壓力梯度考慮在內[7]。Abu-Gharmam等[8]提出的轉捩模型考慮了來流湍流度對臨界動量厚度雷諾數的影響，在無壓力梯度和逆壓梯度下與實驗結果吻合良好，在強順壓梯度下效果較差。Schmidt等[9]基于實驗數據庫[8]發展的轉捩模型無論轉捩點還是轉捩長度都與實驗數據有很好的一致性。

風洞實驗數據在渦輪葉片冷卻設計中起到關鍵作用。國外在這方面起步較早，Nealy等[10]在美國國家航空航天局(National Aeronautics and Space Administration，NASA)穩態風洞中獲得的C3X和MarkⅡ葉片表面換熱數據已經成為驗證數值計算可靠性的經典數據，近年來國外的實驗研究重點是構建實驗數據庫和為改進數值方法提供數據支持[11-13]。國內李靜美等[14]首次在中國科學院力學研究所的激波風洞上進行高速狀態葉片換熱測量。李紅才等[15]在西北工業大學短周期跨聲速葉柵傳熱風洞中研究了維持葉柵氣動狀態穩定的控制方法，以及葉片瞬態換熱測量的實驗方案和換熱數據處理方法[16]，進行了動葉和導葉表面詳細的壓力和換熱測量[17-18]。

數值研究具有周期短、成本低的優點，在分析流動傳熱問題中發揮著越來越大的作用。Kays等[7]采用Patankar-Spalding方法編制了著名的邊界層微分方程計算程序TEXSTAN，可將實驗壓力數據作為邊界條件，通過求解邊界層微分方程獲得換熱系數。實驗數據和數值計算相結合，不僅可以在一定程度上克服實驗周期長、成本高的劣勢，還能獲得相對準確且充足的數據。

前人關于邊界層轉捩發生位置和發展過程做了很多研究[19-21]，而工況改變導致轉捩點變化及其對換熱的影響鮮有報道。現將實驗壓力數據加載到邊界層計算程序TEXSTAN中，采用Schmidt-Patankar轉捩模型[9]研究進口雷諾數和來流湍流度對葉片表面邊界層轉捩的影響機理，并進一步分析轉捩對葉片外換熱的影響，為尋找葉片冷卻薄弱部位提供參考。

1 實驗系統與參數定義

1.1 實驗系統

圖1為葉柵風洞系統。風洞系統由儲氣罐、主流供氣管路、二次流供氣管路和實驗段組成。儲氣罐容積300 m3，最高壓力1.0 MPa，由螺桿式空氣壓縮機充氣。主流管路閥門由截止閥、氣動蝶閥、減壓閥、膨脹節和液壓閥組成，閥門后為流道擴張段、整流穩定段和流道收縮段。整流穩定段流速較低，設置有總壓探針測量葉柵進口總壓。高壓氣體經過主流供氣管路進入實驗段，實驗段由收縮段、進口段和葉柵段組成，在進口段設置7個壓力傳感器測量葉柵進口靜壓。所測葉片放置在葉柵段，葉片實驗件如圖2所示，在葉片壓力面和吸力面分別設置13和19個測壓點。葉柵出口設置壓力傳感器測量葉柵出口靜壓。實驗葉柵參數如圖3所示。葉片弦長88.484 7 mm，柵距75.194 0 mm，進氣角58.2°，出氣角22.7°，壓力面弧長93.749 6 mm，吸力面弧長119.741 8 mm。

圖1 葉柵風洞系統Fig.1 Experimental system photo

圖2 葉片實驗件Fig.2 Experimental blades photo

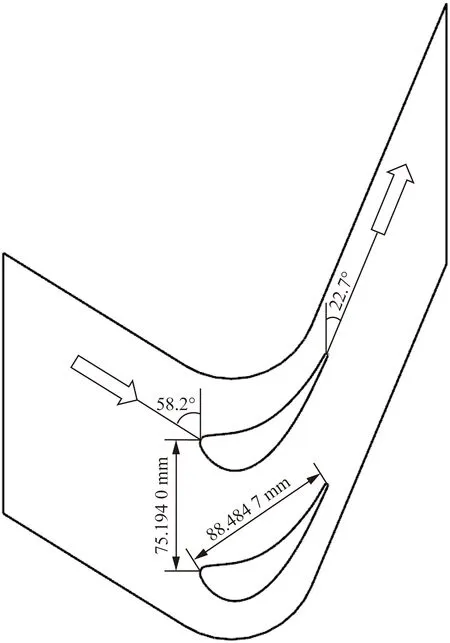
圖3 實驗葉柵參數Fig.3 Experimental cascade parameters

1.2 參數定義

進口雷諾數Re定義為

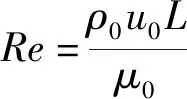
(1)

式(1)中：ρ0為葉柵進口氣流密度，kg/m3；u0為進口速度，m/s；μ0為進口氣流動力黏度，N·s/m2；L為葉片弦長，m。

壓比pr定義為

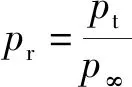
(2)

式(2)中：pt為進口總壓，Pa；p∞為出口靜壓，Pa。

壓力系數Cp定義為

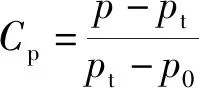
(3)

式(3)中：p為當地靜壓，Pa；p0為進口靜壓，Pa。

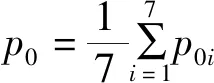
(4)

式(4)中：p0i為進口段壓力傳感器測量壓力值，Pa。

換熱系數h定義為

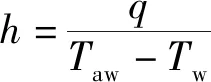
(5)

式(5)中：q為壁面熱流，W/m2；Tw為壁面溫度，K；Taw為葉片表面絕熱壁溫，K。

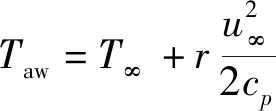
(6)

式(6)中：T∞為主流靜溫，K；r為恢復因子；u∞為主流速度，m/s；cp為比熱容，J/(kg·K)。

2 TEXSTAN計算方法

2.1 控制方程

邊界層質量守恒方程表達式為

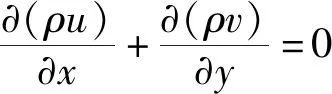
(7)

式(7)中：ρ為密度，kg/m3；u、v分別為x和y方向上的分速度，m/s。

邊界層動量方程表達式為

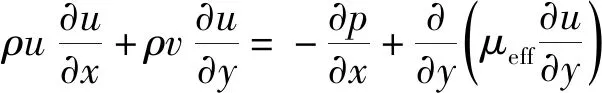
(8)

式(8)中：p為壓力，Pa；μeff為有效動力黏度，N·s/m2。

μeff=μ+μt

(9)

式(9)中：μ為分子動力黏度，N·s/m2；μt為湍流動力黏度，N·s/m2。

邊界層能量方程表達式為

(10)

式(10)中：T為溫度，K；λeff為有效導熱系數，W/(m·K)。

λeff=λ+λt

(11)

式(11)中：λ為分子導熱系數，W/(m·K)；λt為湍流導熱系數，W/(m·K)。

2.2 湍流模型和轉捩模型

計算采用Lam-Bremhorst低雷諾數k-ε湍流模型[22]。該湍流模型依賴的經驗數據較少，可深入到邊界層的黏性底層中，對于層流和湍流邊界層都可求解。方程為

(12)

式(12)中：Sck=1.0，Scε=1.3，C1=1.44，C2=1.92；εM為動量渦流擴散率；k為湍流動能，J；ε為湍流耗散率；υ為運動黏度，m2/s。

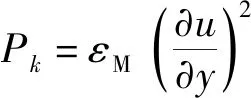
(13)

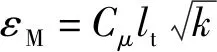
(14)

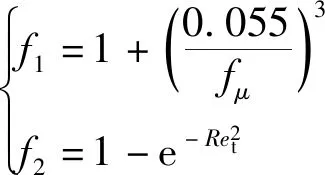
(15)

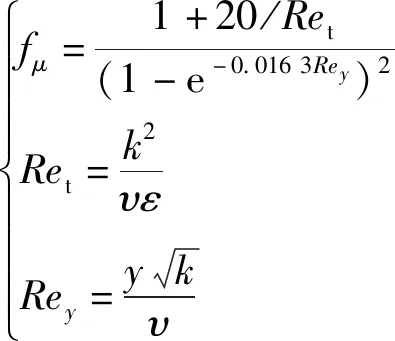
(16)

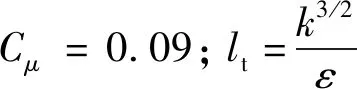
動量厚度是邊界層導致主流動量通量減少的度量，定義為

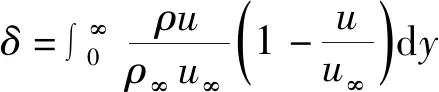
(17)

式(17)中：ρ∞為主流密度，kg/m3；u∞為主流速度，m/s。

動量厚度雷諾數Rem同邊界層的轉捩相關，Rem的定義為

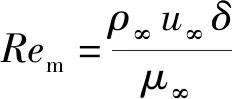
(18)

式(18)中：μ∞為主流動力黏度，N·s/m2。

采用Schmidt等提出的轉捩模型[9]，該模型首先設定k方程中Pk=0，直到動量厚度雷諾數達到125后開始控制Pk項的變化，變化率方程為

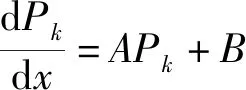
(19)

式(19)中：

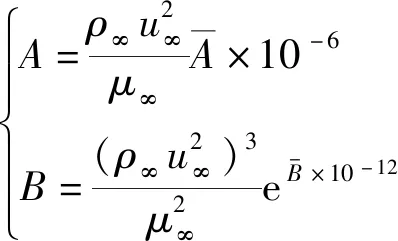
(20)

2.3 邊界條件及網格劃分

進口邊界給定總壓、總溫、進口速度、湍流度。葉片壁面滿足無滑移邊界條件，給定壁面溫度。給定沿流向自由流速度分布。工況參數如表1所示。

表1 計算工況Table 1 Calculation condition parameters

壁面法向第一層網格高度為

y(1)=del99dyi

(21)

式(21)中：del99為邊界層厚度的99%，m；dyi=5×10-5，為程序推薦值。

網格增長率為1.09，直到第n層網格達到

y(n)=0.05del99

(22)

此后網格高度不變。經驗證該網格劃分滿足無關性要求。

3 結果與討論

3.1 壓力測量結果

實驗測量了湍流度為3%，進口雷諾數分別為5×105、6×105和7×105時葉片表面壓力分布。不同工況下葉片表面壓力系數分布如圖4所示，-100%～0表示壓力面相對弧長，0～100%表示吸力面相對弧長，S表示相對弧長。壓力面上，從前緣到6%相對弧長壓力系數下降較快，6%～40%相對弧長變化平緩，在15%～25%相對弧長范圍內出現微弱的逆壓梯度，40%相對弧長之后壓力系數下降明顯，順壓梯度顯著增強。吸力面上，從前緣到28%相對弧長壓力系數快速下降，之后出現逆壓梯度，壓力系數緩慢回升。進口雷諾數增大通過增大壓比實現，所以隨著進口雷諾數增大壓力系數減小。

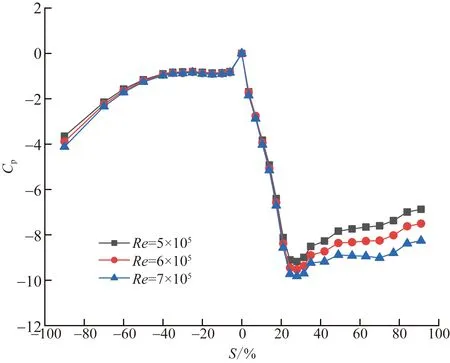
圖4 葉片表面壓力系數分布Fig.4 Distribution of pressure coefficient on blade surface

3.2 計算結果

3.2.1 進口雷諾數對葉片表面流動與換熱的影響

圖5和圖6分別為不同進口雷諾數時葉片表面邊界層流動情況和葉片表面換熱系數分布。動量厚度和動量厚度雷諾數在壓力面40%相對弧長和吸力面28%相對弧長位置分布趨勢發生變化，這與葉片表面靜壓分布密切相關。壓力面上，從前緣到40%相對弧長主流靜壓變化平緩，邊界層自身的發展起主導作用，動量厚度不斷增加，動量厚度雷諾數隨之增加。20%相對弧長之前邊界層流態為層流，層流邊界層變厚導致換熱系數減小。隨后層流開始向湍流轉捩，換熱系數增大。40%相對弧長之后，順壓梯度顯著增強，動量厚度開始減小，但主流速度在強順壓梯度下快速增大，所以動量厚度雷諾數仍然平穩增加，增加速率較之前有所減小，導致邊界層流態一直為過渡態，換熱系數增長趨勢放緩。吸力面上，前緣到28%相對弧長主流靜壓快速下降，雖然動量厚度增加緩慢，但主流速度快速增大使動量厚度雷諾數開始增長。28%相對弧長位置出現逆壓梯度使動量厚度快速增大，雖然在弱逆壓梯度作用下主流速度緩慢減小，但此時動量厚度主導了動量厚度雷諾數的變化，使動量厚度雷諾數加快增長，層流邊界層很快發展為旺盛湍流，之后湍流邊界層變厚同樣引起換熱系數減小。

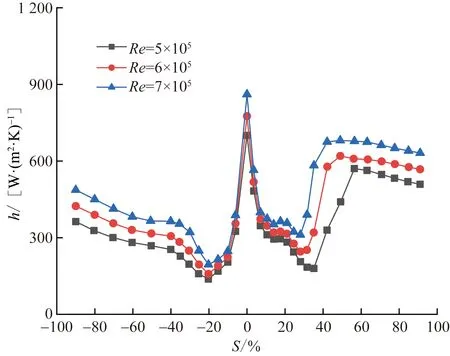
圖6 進口雷諾數對葉片表面換熱系數的影響Fig.6 Effect of inlet Reynolds number on heat transfer coefficient on blade surface

從圖5(a)可以看出，進口雷諾數基本不影響動量厚度，動量厚度雷諾數隨進口雷諾數增大而增長加快，主要由高進口雷諾數時主流速度較大導致，而動量厚度雷諾數加快增長也意味著轉捩提前發生。壓力面上高進口雷諾數工況動量厚度雷諾數增長有限，轉捩點接近。吸力面上Re=6×105和7×105工況轉捩點比Re=5×105工況分別前移3%和7%相對弧長，改變了換熱系數變化趨勢，導致換熱系數沿葉片型面減小的區域縮短，Re=6×105和7×105工況平均換熱系數比Re=5×105工況分別增大15%和32%。

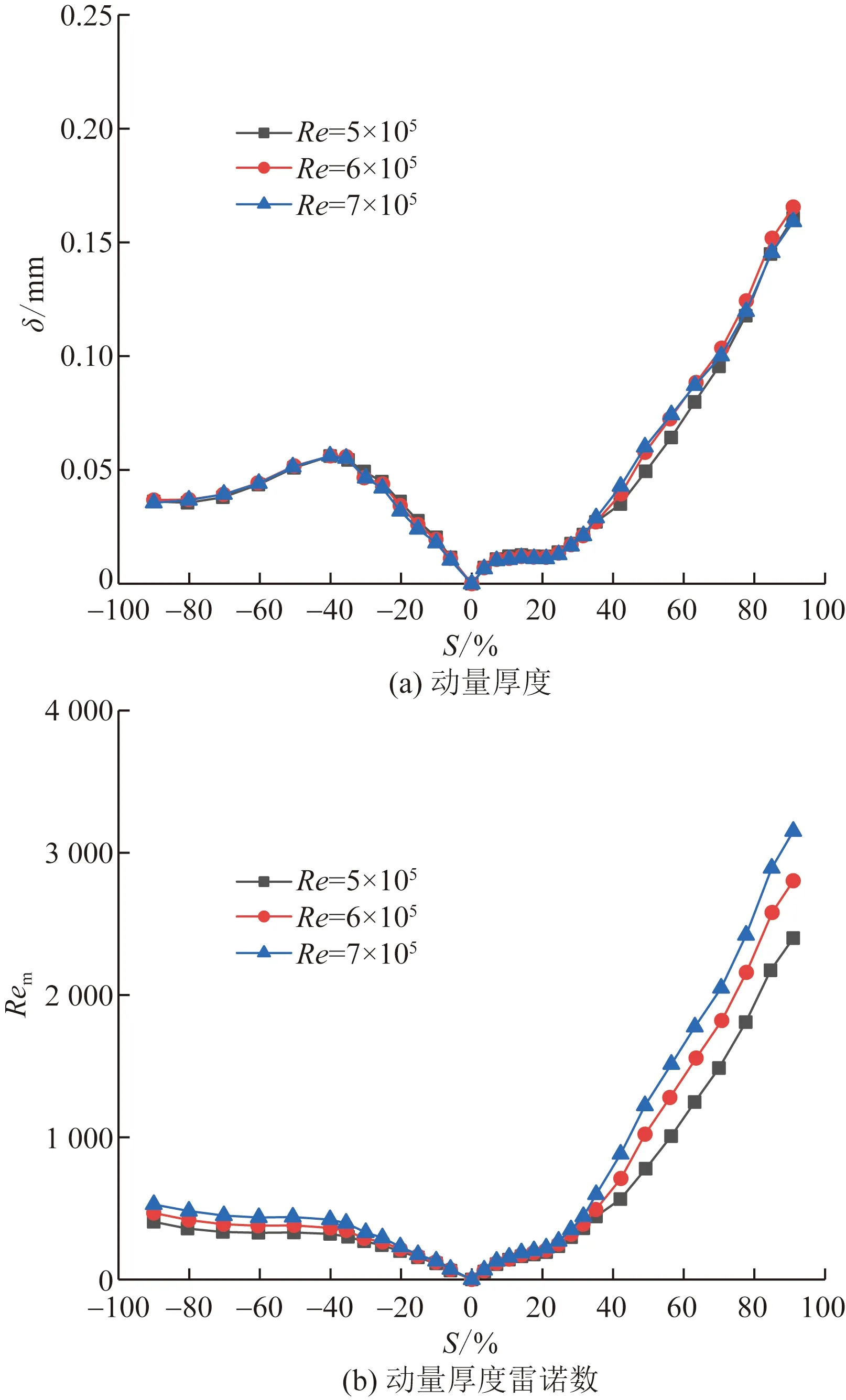
圖5 進口雷諾數對葉片表面邊界層的影響Fig.5 Effect of inlet Reynolds number on boundary layer flow on blade surface

3.2.2 湍流度對葉片表面流動與換熱的影響

圖7～圖10分別為不同湍流度時葉片表面邊界層流動情況和葉片表面換熱系數分布。

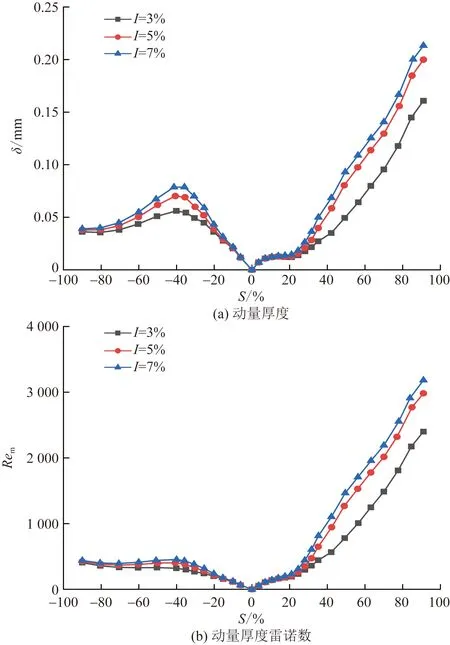
圖7 湍流度對葉片表面邊界層的影響(Re=5×105)Fig.7 Effect of turbulence intensity on boundary layer flow on blade surface (Re=5×105)

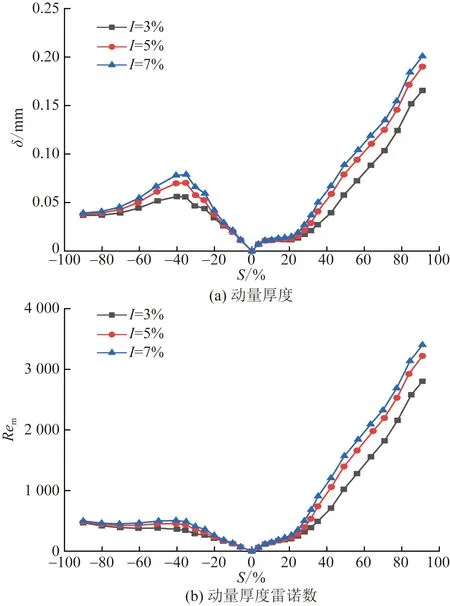
圖8 湍流度對葉片表面邊界層的影響(Re=6×105)Fig.8 Effect of turbulence intensity on boundary layer flow on blade surface (Re=6×105)

圖9 湍流度對葉片表面邊界層的影響(Re=7×105)Fig.9 Effect of turbulence intensity on boundary layer flow on blade surface (Re=7×105)

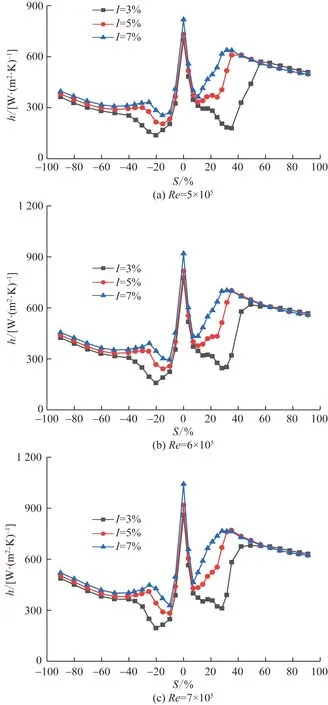
圖10 湍流度對葉片表面換熱系數的影響Fig.10 Effect of turbulence intensity on heat transfer coefficient on blade surface

從圖7(a)、圖8(a)和圖9(a)可以看出，湍流度增大使動量厚度增大，因此動量厚度雷諾數增長加快，造成轉捩點前移。壓力面上具有大范圍的順壓梯度，穩定性較好，湍流度的影響較小。壓力面上I=5%和7%工況轉捩點比I=3%工況分別前移5%～9%和8%～10%相對弧長，吸力面上分別前移17%～22%和19%～24%相對弧長。湍流度對換熱系數的影響主要源于對轉捩點的影響，轉捩點前移使換熱系數減小的范圍縮短，且湍流度對壓力面換熱的影響弱于吸力面。壓力面上I=5%和7%工況平均換熱系數比I=3%工況分別增大16%～17%和33%～34%，吸力面上分別增大19%～23%和35%～41%。

4 結論

(1)葉片表面邊界層流動與壓力分布密切相關。順壓梯度使主流速度增大，但動量厚度增速放緩甚至開始減小，動量厚度雷諾數增加速率減小，導致層流難以向湍流過渡。逆壓梯度造成動量厚度急劇增大，主導了動量厚度雷諾數的變化，使動量厚度雷諾數加快增長，層流邊界層很快發展為旺盛湍流，可見逆壓梯度會促使邊界層轉捩。因此可以通過適當改進葉片外形，調控葉片表面壓力分布，有效控制邊界層轉捩的可能范圍。

(2)進口雷諾數基本不影響動量厚度，動量厚度雷諾數隨進口雷諾數增大而增長加快，主要由高進口雷諾數時主流速度較大導致，而動量厚度雷諾數加快增長也意味著轉捩提前發生。壓力面上高進口雷諾數工況動量厚度雷諾數增長有限，轉捩點接近，吸力面上轉捩點前移3%～7%相對弧長。進口雷諾數增大使葉片表面平均換熱系數增大15%～32%。

(3)湍流度增大使動量厚度增大，因此動量厚度雷諾數增長加快，造成轉捩點前移。壓力面上具有大范圍的順壓梯度，穩定性較好，湍流度的影響較小。湍流度增大使壓力面轉捩點前移5%～10%相對弧長，平均換熱系數增大16%～34%，吸力面轉捩點前移17%～24%相對弧長，平均換熱系數增大19%～41%。

(4)不同進口雷諾數和來流湍流度下葉片表面邊界層轉捩位置不同，受實際情況影響，轉捩點變化范圍內都可能出現換熱突然增強，因此要有針對性地強化該區域冷卻設計。