基于深度殘差反向傳播神經網絡的鋼筋腐蝕檢測

林旭梅，胡 川，朱廣輝，陳一戈，苗芳榮

(青島理工大學信息與控制工程學院，青島 266520)

海水是一種富含侵蝕性鹽類的腐蝕電解質溶液[1]，架駐在海洋環境下的鋼筋混凝土工程在漫長服役期里易遭受腐蝕侵壞，其中內部鋼筋的腐蝕是造成混凝土結構工程耐久性失效的主要原因，因此提高對服役鋼筋損傷狀態的檢測精度，及時對危險工程做出預判尤為重要。

近年來，中外學者對鋼筋混凝土腐蝕檢測做出大量研究，Gotoh等[2]利用鋼筋銹蝕過程中磁導率產生變化這一特性，利用電磁感應原理結合霍爾元件來檢測鋼筋銹蝕程度。王瀟舷等[3]通過研究鋼筋銹蝕應變力的變化結合數字圖像技術實現對混凝土內部腐蝕程度的檢測。V?lker等[4]將探地雷達引入混凝土腐蝕檢測之中，通過測量鋼筋反射振幅，電勢等特征數據，采用機器學習方法對數據進行融合處理來判斷鋼筋銹蝕程度。

陽極梯傳感器在海洋工程鋼筋腐蝕監測中被廣泛應用[5]，現采用陽極梯傳感器監測系統對腐蝕樣本數據進行采集，將采集的腐蝕電壓、腐蝕電流、腐蝕阻抗及環境溫度等特征參數作為模型的輸入，鋼筋的腐蝕狀態作為模型輸出。針對小樣本數據下淺層神經網絡模型擬合能力不足，而加深網絡層數出現網絡性能退化問題，建立雙跳躍深度殘差網絡模型，同時對Adam算法中影響學習率的二階矩估計梯度進行調整，并將其用于鋼筋混凝土腐蝕狀態預測。

1 陽極梯傳感器數據預處理及分類模型

1.1 鋼筋混凝土腐蝕狀態預測模型

鋼筋混凝土腐蝕狀態與各特征之間具有強耦合性，常規數學建模往往無法準確全面地反映出各因素與腐蝕程度之間的高度復雜關系。因此，采用神經網絡模型對鋼筋混凝土腐蝕程度進行判別，利用其強大的非線性映射能力，從預處理后的數據中直接提取特征，自動學習擬合各特征量與輸出標簽間的函數關系，避免了復雜的數學建模過程。鋼筋混凝土腐蝕檢測模型結構如圖1所示。

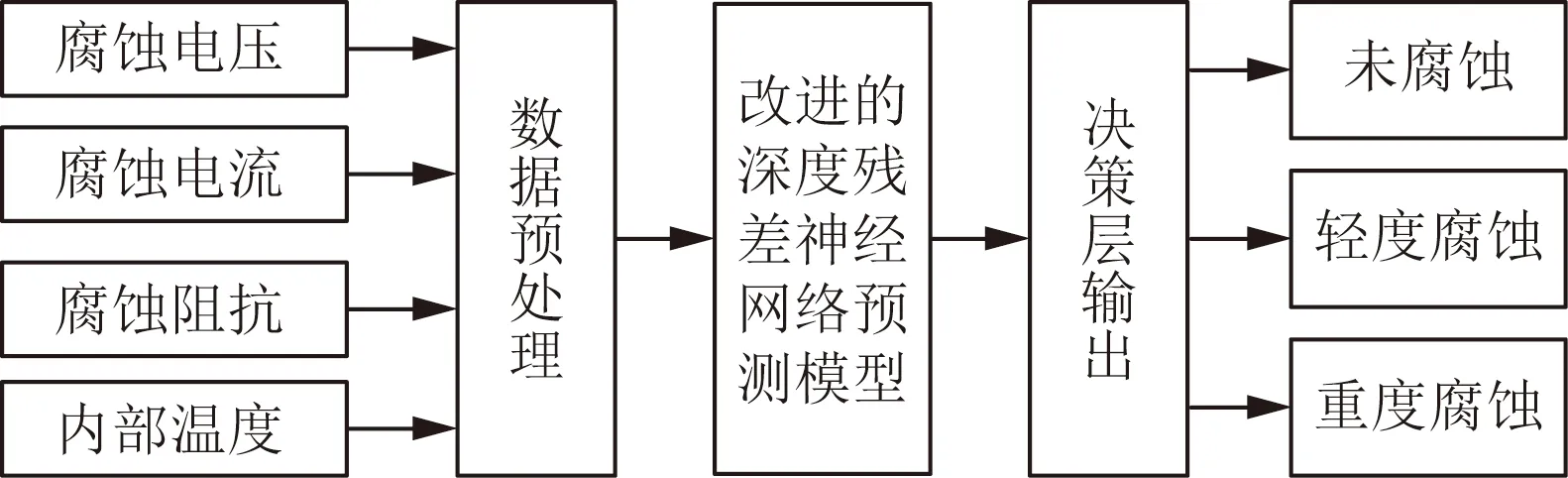
圖1 鋼筋混凝土腐蝕監測模型結構圖Fig.1 Structure diagram of reinforced concrete corrosion monitoring model

1.2 陽極梯監測數據預處理

數據集中于陽極梯測得的腐蝕電壓、腐蝕電流、腐蝕阻抗、環境溫度特征量綱各不相同，且數值之間存在較大差異，使用梯度下降法時勢必會減緩梯度的尋優速度。因此，使用min-max歸一化方法對上述特征值進行歸一化處理，消除不同特征之間的量綱影響，且使損失函數無論從任何位置開始，使用梯度下降法都能更迅速地找到最小值，加速模型的收斂速度，公式為

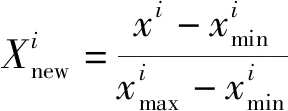
(1)

f(x)=max(0,x)

(2)

式(2)為激活函數Relu表達式,其具有擬合非線性的能力[6]。

數據集中鋼筋銹蝕數據的標簽分成“未腐蝕”“輕度腐蝕”“重度腐蝕”3類。為了將類別變量轉換成計算機能夠識別的形式，采用One-hot編碼。如表1所示。

表1 One-hot編碼Table 1 One-hot coding

2 改進雙跳躍深度殘差BP神經網絡模型

2.1 雙跳躍殘差網絡模塊

基于傳統反向傳播(back propagation,BP)神經網絡的鋼筋混凝土腐蝕分類方法，在樣本規模相對較小的情況下，當網絡層數達到一定深度時，網絡的擬合能力將達到飽和，其分類準確率很難再得到提升[7]。若繼續加深網絡層數，則會導致網絡退化。為了提高鋼筋腐蝕分類準確率，提出雙跳躍深度殘差BP神經網絡模型。

所提的雙跳躍殘差神經網絡模塊如圖2所示，在傳統神經網絡結構基礎上引入雙跳躍連接，每個殘差模塊使用3個同維度的網絡層進行堆疊，分別在網絡的一層到二層、一層到三層之間加入跳躍連接，在不增加額外參數的基礎上構成雙跳躍連接殘差神經網絡模塊，加強特征信息在網絡層間的傳遞和利用。這里規定一層到二層的跳躍連接用S1表示，一層到三層間的跳躍連接用S2表示。

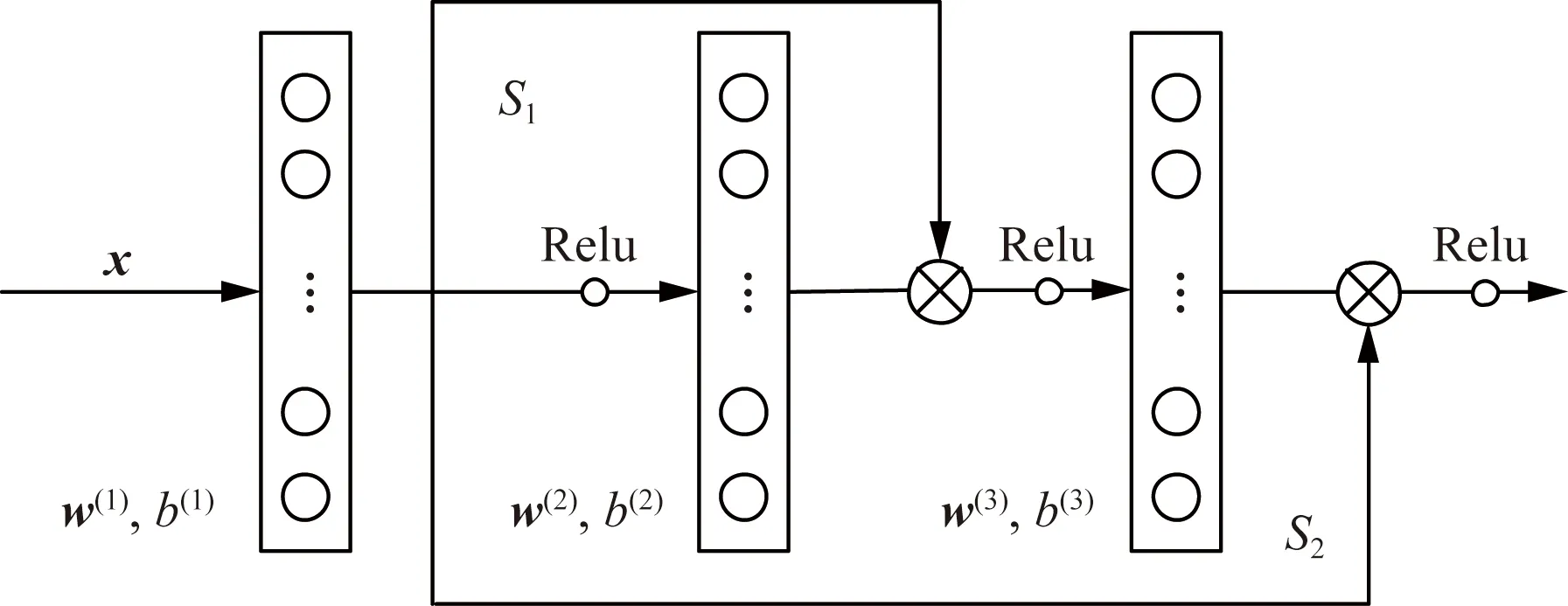
圖2 雙跳躍殘差神經網絡模塊Fig.2 Double jump residual module

在單個殘差模塊中，對輸入樣本的處理主要包括以下3個步驟。

步驟1特征向量x作為殘差網絡模塊的輸入，經過第一層的權值線性加權后輸出為f1(x)，R(·)表示Relu激活函數。

f1(x)=w(1)x+b(1)

(3)

F1(x)=R[f1(x)]

(4)

式中：w(1)、b(1)分別為第一層的權重和偏置參數；F1(x)為對f1(x)激活后的輸出。

步驟2將第一層激活后的非線性輸出F1(x)作為第二層網絡的輸入，經過加權偏置后輸出f2(x)；f2(x)與第一層的跳躍連接f1(x)相加，經過Relu激活后輸出F2(x)。

f2(x)=w(2)F1(x)+b(2)

(5)

f21(x)=f2(x)+f1(x)

(6)

F2(x)=R[f21(x)]

(7)

式中：w(2)、b(2)分別為第二層的權重和偏置參數；f21(x)為第一層的跳躍信息輸出與第二層線性信息輸出的疊加，實現了淺層特征重用。

步驟3將第二層的非線性輸出F2(x)作為第三層網絡的輸入，經過加權偏置后輸出f3(x)。H(x)表示加上跳躍連接后殘差模塊期望擬合的基礎映射，經過激活后輸出為F3(x)。

f3(x)=w(3)F2(x)+b(3)

(8)

H(x)=f3(x)+f1(x)

(9)

F3(x)=R[H(x)]

(10)

式中：w(3)、b(3)分別為第三層的權重和偏置參數。式(9)將傳統堆疊層非線性映射轉換為加有跳躍連接的殘差映射。傳統堆疊層網絡隨著深度的增加，經過逐層映射后所表達信息的非線性復雜度也在增加，其擬合恒等映射的能力卻在下降，通過跳躍連接，將傳統深度BP神經網絡難以擬合的恒等映射轉化為更容易學習的殘差映射[8]。

式(9)不僅能利用跳躍傳播使低層信息得到充分利用，也能帶來很好的反向傳播效果，用L表示損失函數，使用梯度下降法來表示S2跳躍連接層之間的梯度傳遞過程。根據反向傳播的鏈式求導法則有

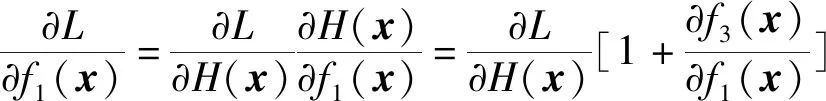
(11)

由式(11)可知，梯度?L/?f1(x)由兩部分組成，一部分由?L/?H(x)直接傳播梯度信息到淺層而不涉及任何權重層，從而保證了梯度信息的反向有效傳遞。另外一部分則是?L/?H(x)與?f3(x)/?f1(x)的鏈式乘積，梯度信息的傳遞需要經過中間權重層，如果中間權重層的梯度信息很小，經過鏈式連乘后到達淺層的梯度信息會變得更小，可能導致梯度消失現象，從而使優化變得困難[9]。正是由于跳躍連接引入的額外梯度?L/?H(x)，使得梯度信息能直接從深層反向跨越傳遞到淺層，避免了梯度消失問題，使得網絡更容易優化。

2.2 Adam優化算法

Adam算法[10]是一種基于低階矩自適應估計的隨機目標函數的一階梯度優化算法。該算法易于實現，計算效率高，對內存的需求小，被廣泛應用于深度學習訓練中，Adam算法過程如表2所示。

由表2可以看出，Adam算法中的學習率由mt和vt共同控制調整，mt為gt的一階矩估計加權平均梯度，可將其看做當前預測梯度的近似，即從過去歷史的梯度來預測下一步應該得到的梯度。

表2 Adam算法Table 2 Adam algorithm

引入步長退火思想使用一階矩估計加權平均梯度mt對二階矩估計加權平均梯度vt進行調整，改進后的公式為

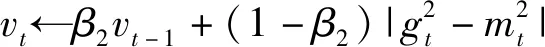
(12)

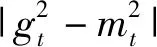
2.3 雙跳躍深度殘差BP神經網絡模型

模型共堆疊了4個雙跳躍殘差模塊構成雙跳躍深度殘差BP神經網絡，如圖3所示，每個殘差模塊均包含3個基礎層，其中第Ⅰ、Ⅲ模塊中每個基礎層的神經元個數為128個，第Ⅱ、Ⅳ模塊中每個基礎層的神經元個數為64個。模型的輸入xi為具有21個特征的列向量，輸出為3個類別概率分布的列向量，模型選擇其中最大概率值對應類別為預測標簽[11]。

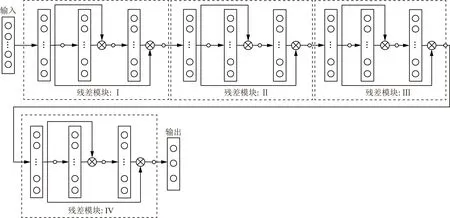
圖3 雙跳躍深度殘差BP神經網絡模型Fig.3 Double jump depth residual BP neural network model

傳統BP神經網絡通過神經元的逐層非線性映射來實現復雜分類函數的擬合，其具有一定的自學習和決策能力。但在小樣本數據下，當網絡層數達到一定深度時，網絡的擬合性能將達到飽和，若繼續加深網絡層數，則會導致網絡性能下降，產生網絡退化現象。因此，現通過構建殘差神經網絡模塊來增強特征信息在非線性層間的傳遞，增加雙重跳躍連接實現低非線性度特征信息的重復充分利用。將改進的Adam算法與雙跳躍深度殘差神經網絡相結合，對鋼筋混凝土的腐蝕程度進行預測分類。

3 實驗及結果分析

3.1 實驗平臺及方法

實驗在Windows 10系統環境下，采用谷歌開發的TensorFlow 2.2-GPU版本深度學習平臺進行網絡訓練，實驗中網絡模型程序由python3.7編寫完成。使用的鋼筋混凝土腐蝕檢測數據共有4 500條，其中未腐蝕數據、輕度腐蝕數據、重度腐蝕數據各1 500條。在訓練過程中，前l-1層均使用Relu函數進行激活，最后一層l采用Softmax函數激活輸出。

將數據集分別按照6∶4、7∶3、8∶2的比例分為訓練集(T1～T3)和測試集(P1～P3)，在訓練過程中，設置迭代次數為500次，分別用Adam算法優化6層，14層普通BP神經網絡和14層殘差神經網絡及本文所提改進Adam算法優化14層殘差神經網絡。上述4種算法模型在各自比例測試集下的測試準確率與測試損失誤差趨勢變化如圖4～圖9所示。

3.2 實驗對比分析

對比分析圖4～圖9中在不同比例測試數據集上的準確率、損失誤差的變化趨勢可知，將Adam算法優化的普通BP網絡從6層加深至14層時，訓練過程中，曲線波動較大，難以收斂，反映出普通深度BP神經網絡在小樣本數據下其網絡擬合能力退化，泛化性能弱的缺點；用Adam算法優化的雙跳躍殘差神經網絡，由于其增加了雙重跳躍連接實現低非線性度特征信息的重復充分利用，其性能較為改善；利用所提改進Adam算法優化雙跳躍殘差神經網絡其收斂速度及擬合性能均有明顯提升。

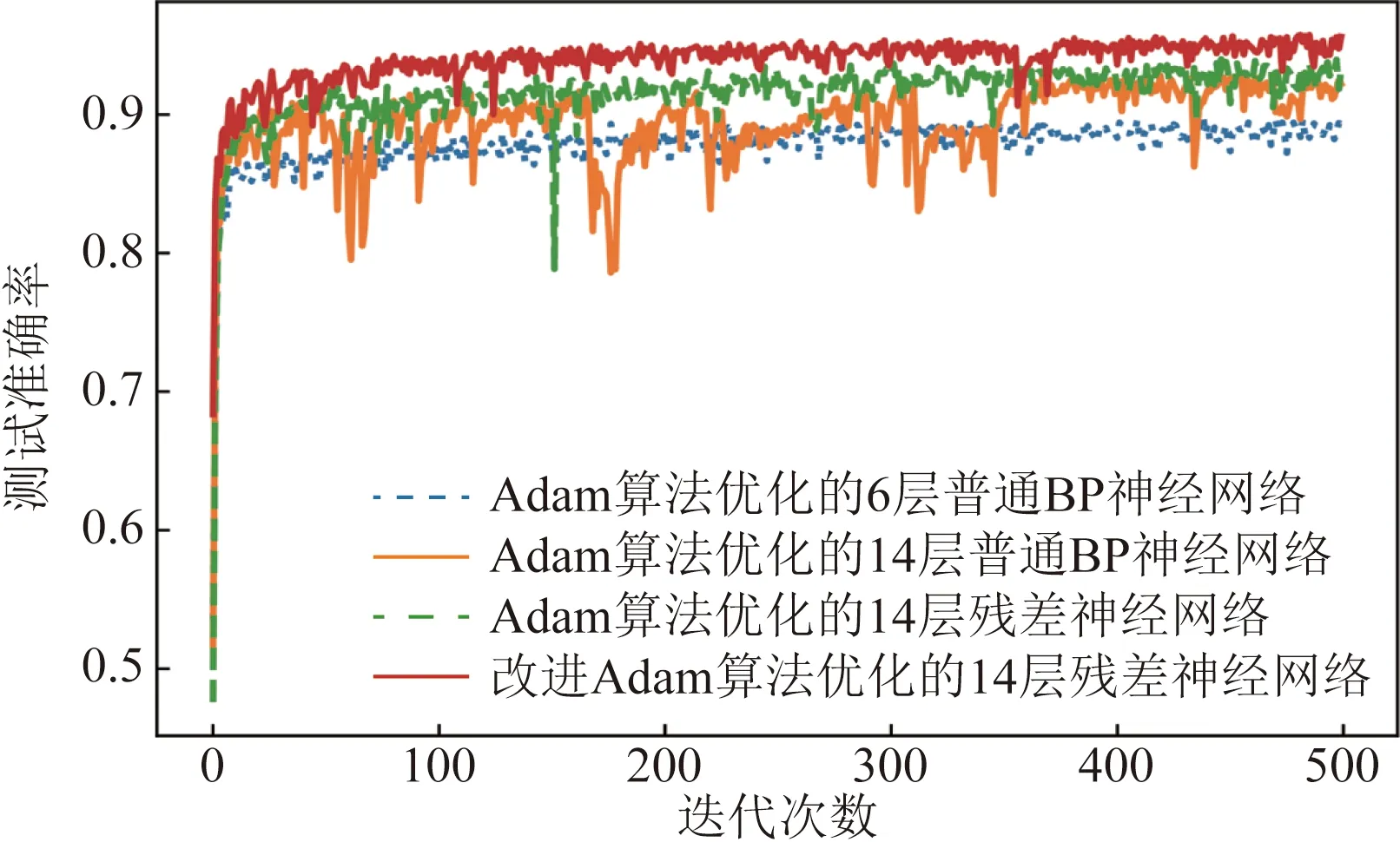
圖4 P1測試集下的測試準確率Fig.4 Test accuracy under test setP1

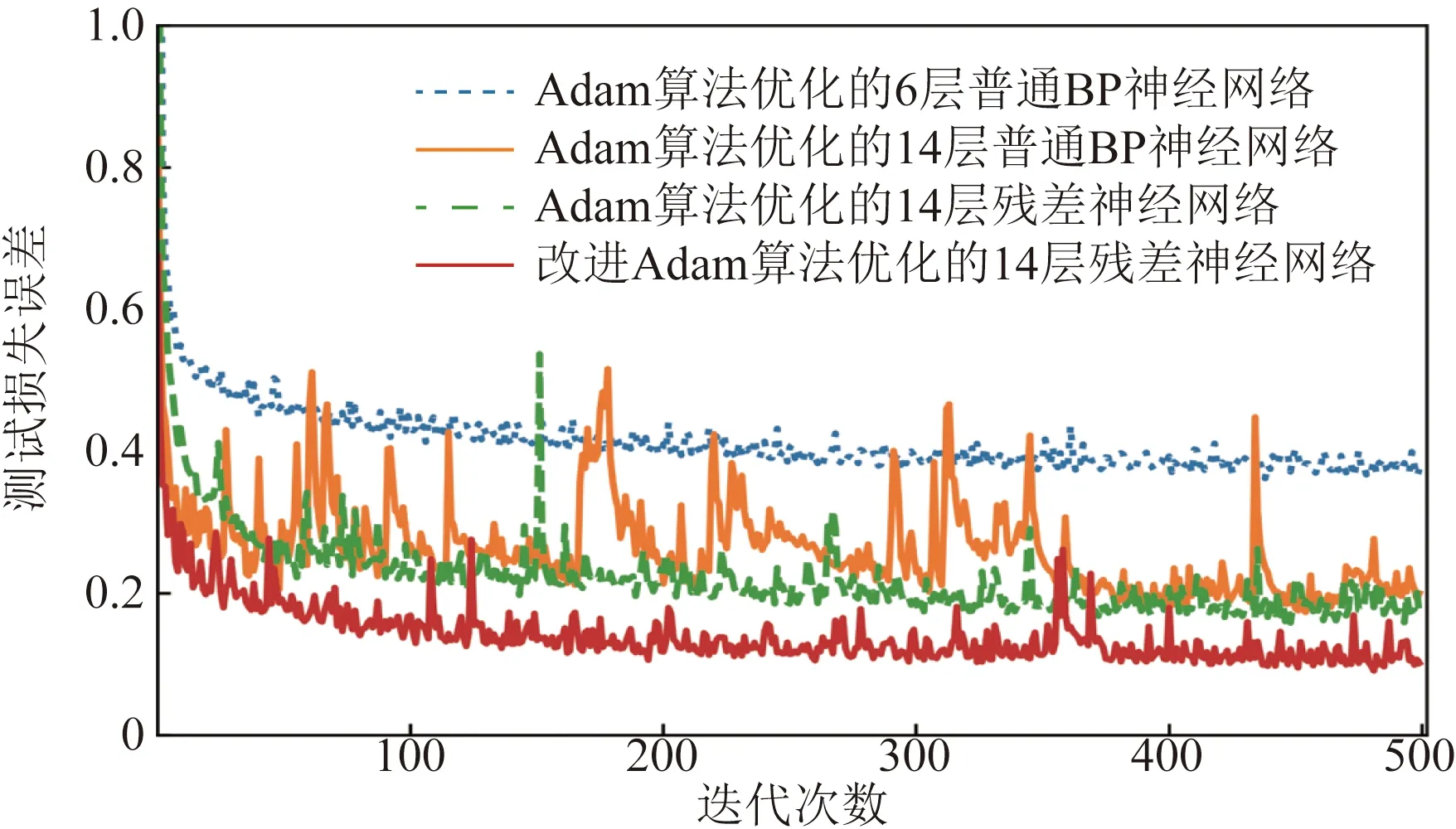
圖5 P1測試集下的測試損失誤差Fig.5 Test loss error under test setP1

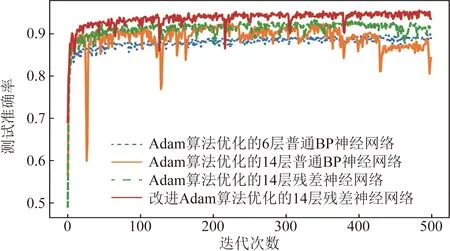
圖6 P2測試集下的測試準確率Fig.6 Test accuracy under test setP2

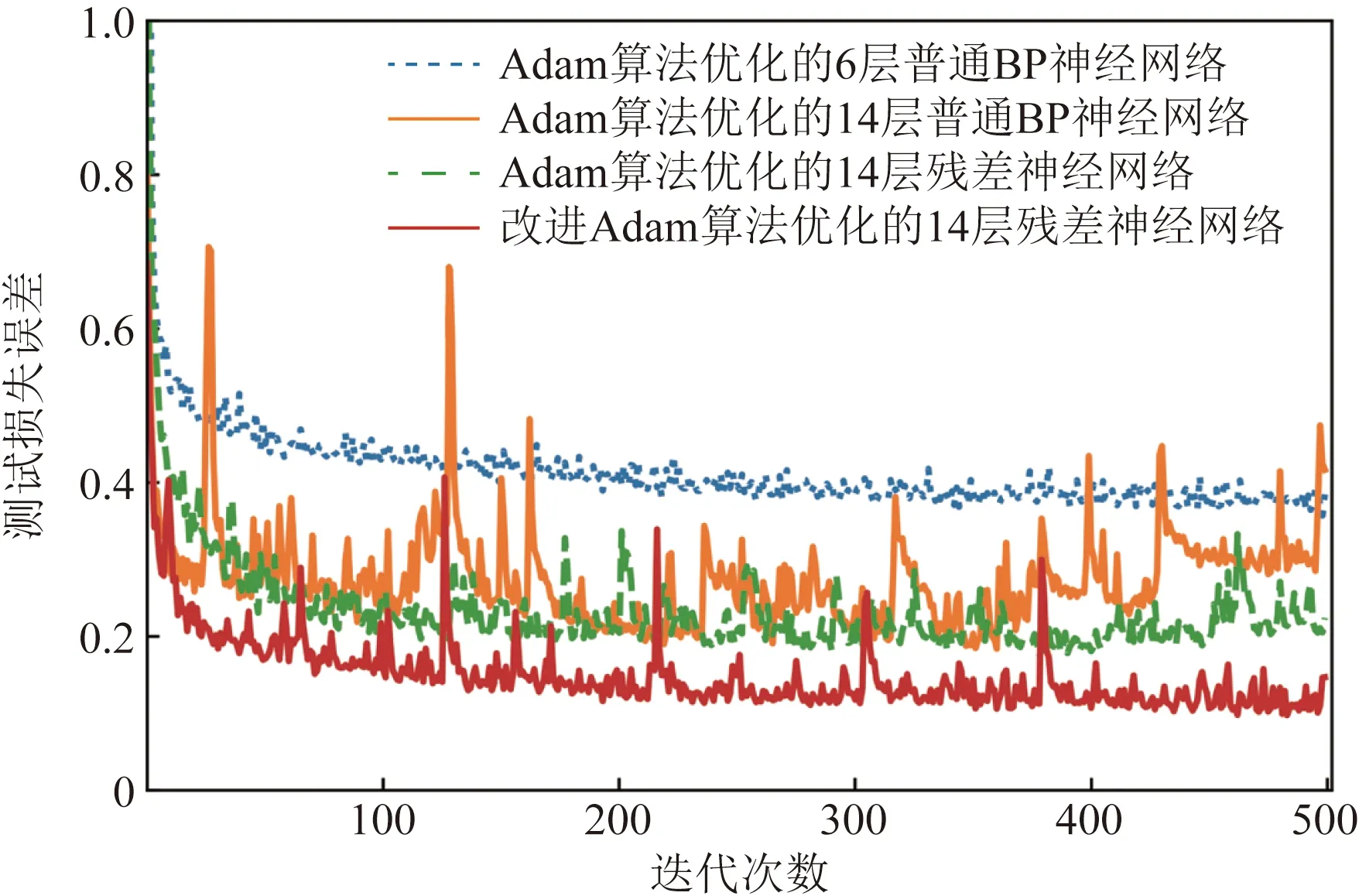
圖7 P2測試集下的測試損失誤差Fig.7 Test loss error under test setP2

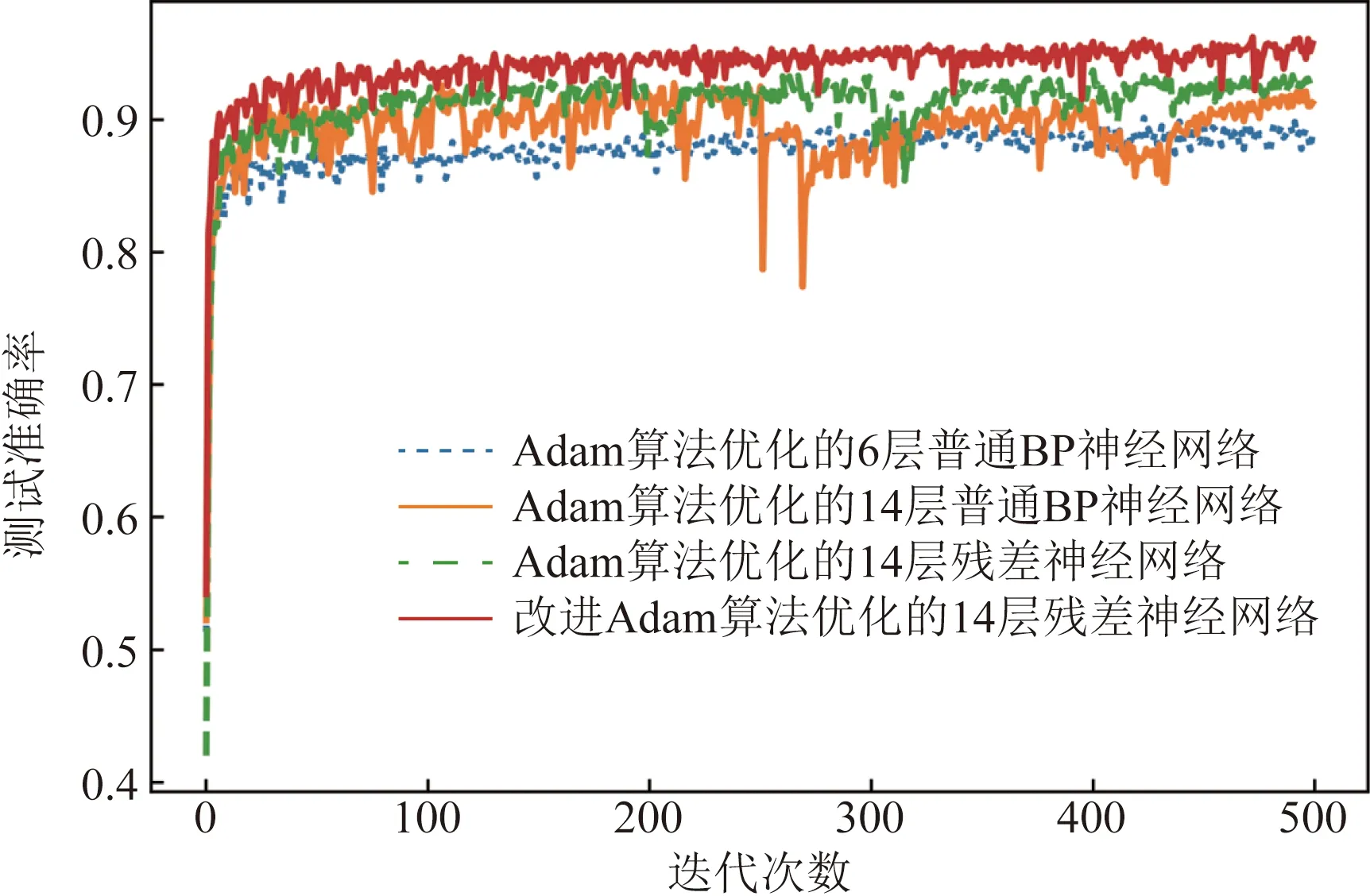
圖8 P3測試集下的測試準確率 Fig.8 Test accuracy under test setP3

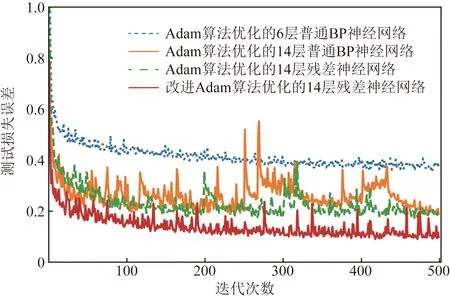
圖9 P3測試集下的測試損失誤差Fig.9 Test loss error under test setP3

4 結論

針對小樣本數據下鋼筋混凝土腐蝕狀態檢測方法單一且精度不高等問題，提出一種利用改進Adam算法優化雙跳躍深度殘差神經網絡檢測鋼筋混凝土腐蝕狀態的預測方法。

(1)建立了雙跳躍深度殘差神經網絡模型，該模型能加強了淺層低非線性度特征信息在不同網絡層間的跨越傳遞和重復利用，同時在反向傳播過程中避免了梯度消失，相比較淺層和傳統深度BP神經網絡具有更好的預測分類性能。

(2)引入步長退火思想對Adam算法進行改進，使用一階矩估計加權平均梯度對二階矩估計加權平均梯度進行調整，促使算法合理動態調整學習率，加速算法的全局尋優能力，使目標函數在不陷入局部極小值的前提下盡快收斂。

(3)仿真表明，改進Adam算法優化的雙跳躍深度殘差神經網絡模型在小樣本數據下具有更好的預測分類性能。