動力傳動軸-機匣系統耦合振動特性

龍 倫，李 堅，趙勇銘，王 迪

(中國航發湖南動力機械研究所結構強度研究部，株洲 412002)

動力傳動軸是直升機傳動系統的重要動力傳輸部件之一[1-3]，其一端與發動機連接，另一端通過聯軸器(如膜盤、膜片)與主減速器相連，從而實現將發動機功率和轉速傳輸到主減速器，因此其振動特性好壞直接影響到整個傳動系統工作的穩定性。以往對于動力傳動軸振動特性的研究主要集中在單個傳動軸臨界轉速計算分析[4-6]、軸系的扭轉分析[7-9]以及軸系齒輪系統動力特性分析[10-11]等，在這些分析中一般根據工程經驗認為支承機匣剛性很強，忽略了支承機匣的柔性，從而造成了一定的計算誤差，并且這種誤差隨著因支承機匣重量減輕、剛度減弱導致的轉靜子耦合動力特性越明顯而越大，這嚴重地制約了直升機傳動系統的動力學設計。針對以上情況，中外研究人員開展了相關研究工作，Guo等[12]開展了考慮柔性箱體結構的單級定軸齒輪箱振動特性研究；郭天才等[13]在尾減減速器機匣改進設計時避開了傳動軸的共振頻率；漆文凱等[14]進行了基于轉靜子耦合的組合壓氣機振動特性研究；許華超等[15]分析比較了耦合和不耦合柔性機匣結構時主減速器的振動特性，但在直升機傳動系統中開展傳動軸-機匣的耦合振動特性研究還比較少，并欠缺開展針對性的研究試驗。

現以某型傳動系統中的動力傳動軸-減速器機匣為研究對象，建立考慮傳動軸-機匣結構耦合振動分析模型，結合轉靜子系統耦合振動機理對計算結果進行分析，并開展試驗驗證。

1 轉靜子系統耦合振動機理

對于轉子系統而言，系統的動能為

(1)

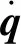
系統的應變能為

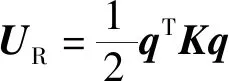
(2)

式(2)中：K為對稱的剛度矩陣。

系統阻尼力的虛功為

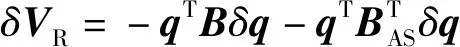
(3)

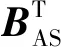
對于靜子系統而言，系統的動能為

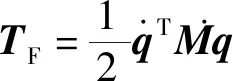
(4)

系統的應變能為

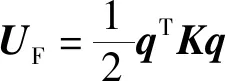
(5)

系統阻尼力的虛功為

δVF=-qTBδq

(6)

相互作用單元是指轉子與靜子之間的連接結構，如軸承等，其動力特性可以表示為

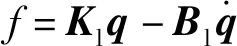
(7)

矩陣Kl和Bl可以分解成對稱和反對稱兩部分，即

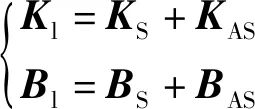
(8)

式(8)中：KS與定常彈性力有關，KAS與非定常彈性力有關，BS與陀螺力有關，BAS與結構阻尼力有關。

其虛功為

(9)

運用哈密爾頓原理，可得

(10)

式(10)中:δVe為激勵力的虛功。

將式(1)～式(9)代入式(10)可得轉靜子系統的動力學方程為

(11)

當不考慮非線性連接力時，系統的齊次方程式可簡化為

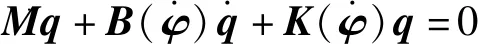
(11)

該方程的特征解和特征向量對應系統的固有頻率和振型。從上述方程中可以看出，當相互作用單元對系統阻尼矩陣、剛度矩陣影響較大時，會出現不同于單獨轉子或靜子系統的特征值和特征向量，即出現轉靜子系統耦合振動。

2 動力傳動軸-機匣系統有限元建模

2.1 結構簡介

某型傳動系統如圖1所示，系統通過動力傳動軸轉子組件實現減速傳動，將發動機的輸入轉速及功率傳遞給主減主組件。動力傳動軸轉子組件分別安裝在減速器機匣的左、右兩側，設計的輸入轉速為20 900 r/min，最大輸入功率2 000 kW。

動力傳動軸轉子組件主要包括動力傳動軸、輸出錐齒輪、輸入齒輪軸、膜片聯軸器等零部件。其中輸出錐齒輪通過前端的無內圈帶安裝邊圓柱滾棒軸承(1#支承)及后端雙排滾子軸承(2#支承)安裝在減速器機匣的軸承座上，輸入齒輪軸通過接觸球軸承(3#支承、4#支承)支撐在試驗器車臺剛性機匣上，動力傳動軸轉子組件結構及安裝示意圖如圖2所示。

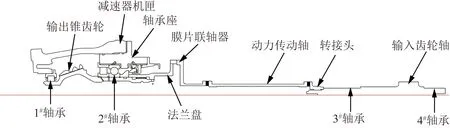
圖2 動力傳動軸轉子組件結構及安裝示意圖Fig.2 Schematic diagram of structure and installation of power transmission shaft rotor assembly

2.2 系統耦合振動分析模型

采用三維實體單元對動力傳動軸-機匣系統進行網格劃分，系統有限元模型如圖3所示。模型中螺栓結構按等效質量和等效轉動慣量以集中質量的方式施加；膜片聯軸器結構采用彈簧單元模擬，彈簧單元剛度值通過實測膜片聯軸器剛度獲得，本系統中膜片聯軸器的實測軸向、扭轉、彎曲剛度分別為2.7×103、2.1×105和1.2×104N ·m/rad；根據系統所使用軸承滾珠數目、直徑、接觸角等參數，參照文獻[16]中的軸承剛度近似公式求得4個軸承的剛度量級在108N/m，故模型中軸承剛度取1×108N/m。為了保證系統模型中轉子部件與靜子部件在連接處(軸承位置)的位移協調，模擬軸承的彈簧單元節點分別通過模型預測控制(model predictive control，MPC)的形式與轉子部件、靜子部件相關聯。

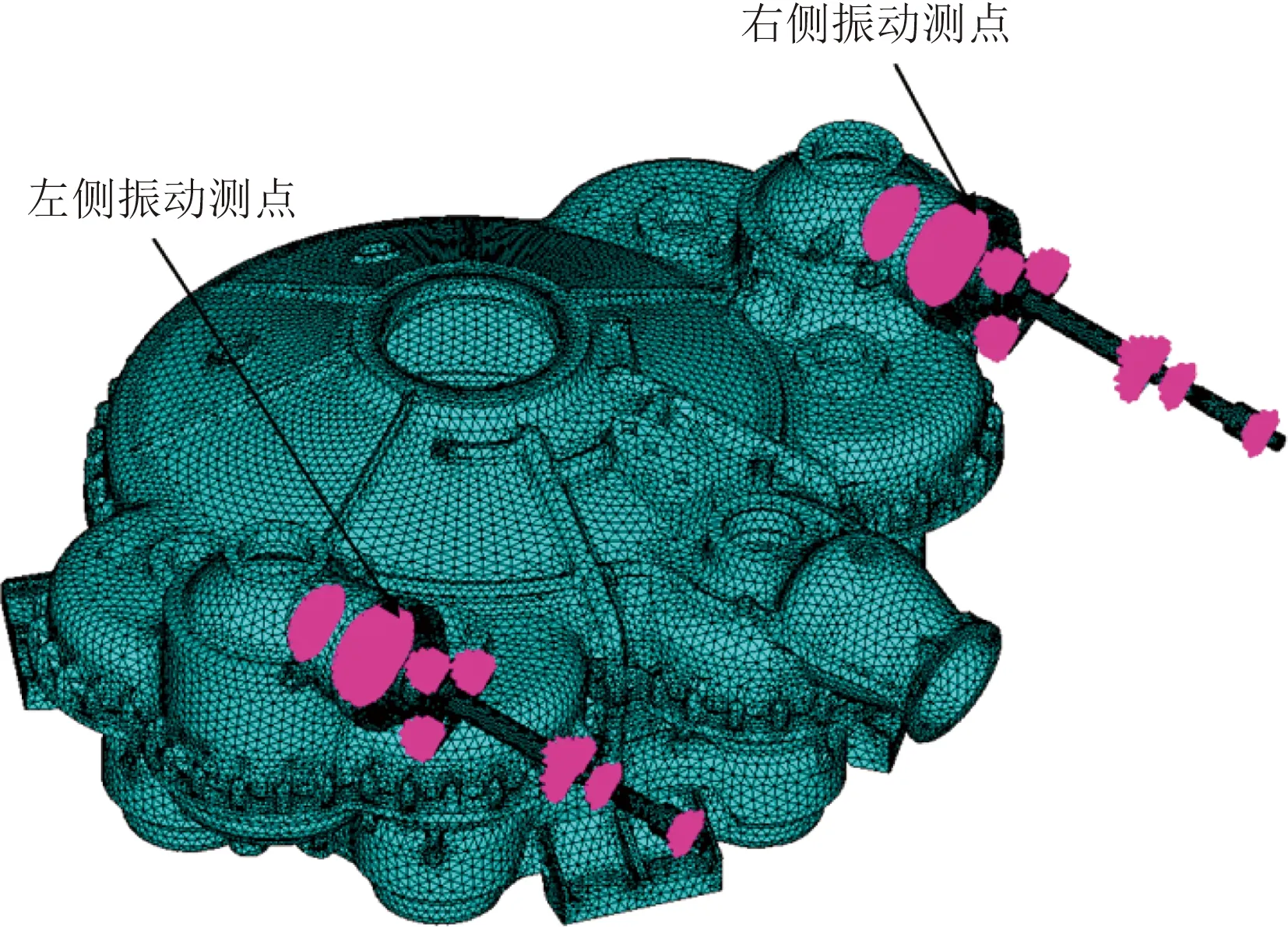
圖3 動力傳動軸-機匣系統有限元模型Fig.3 Finite element model of the power driving shaft-casing system

考慮到系統中轉子部件均采用不銹鋼材料，材料阻尼較低，故仿真分析時只考慮系統的結構阻尼。根據工程經驗，模型中系統結構阻尼比取0.02。

3 動力傳動軸-機匣系統耦合振動分析

為了掌握動力傳動軸-機匣系統在設計轉速范圍下的振動特性，對系統進行不平衡響應計算分析。分析中，在動力傳動軸轉子組件上施加轉速、不平衡等載荷，不平衡量大小為20 g·mm，施加于右側動力傳動軸轉子組件的輸出錐齒輪的齒輪面上。提取與試驗測試中振動加速度傳感器布置位置(圖3)相同處的節點振動響應，其中軸向、垂直、水平方向的振動速度響應-轉速結果如圖4所示，對應峰值轉速下系統共振振型如圖5所示。測點在25 000 r/min轉速范圍內存在4個峰值轉速分別為13 200、15 000、16 800和21 600 r/min。

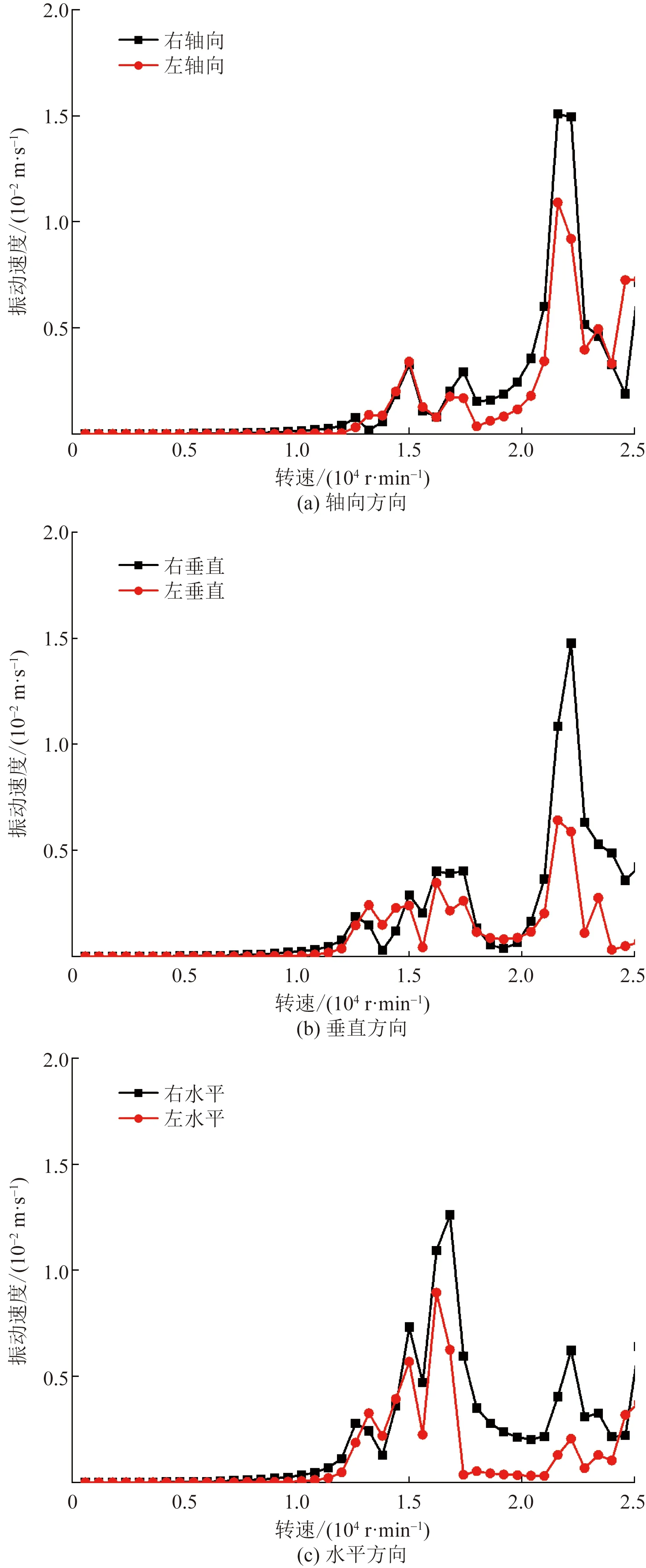
圖4 不同方向振動速度響應-轉速曲線Fig.4 Velocity response speed curves at different vibrations

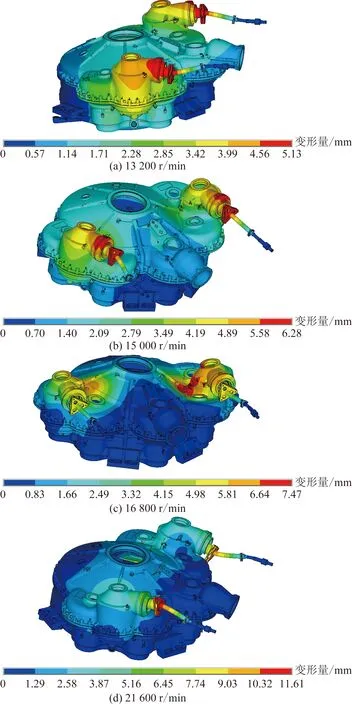
圖5 不同峰值轉速對應系統振型Fig.5 Different peak speed corresponding to system mode shape

系統在13 200 r/min峰值轉速時，垂直、水平方向上的振動響應較大；在15 000 r/min和16 800 r/min峰值轉速時，水平方向上的振動響應較大；在21 600 r/min峰值轉速時，軸向、垂直方向上的振動響應較大。

系統13 200 r/min和15 000 r/min峰值轉速對應的系統振型在連接處存在較大振動位移，結合本文第1節所述的系統耦合振動機理可知，該2階振動為系統的耦合振動。其中13 200 r/min峰值轉速對應振型主要表現為動力傳動軸-機匣系統耦合的上下擺動，左、右振動測點位置垂直方向上的相位相差在180°左右；15 000 r/min峰值轉速對應振型主要表現為動力傳動軸-機匣系統耦合的左右擺動，左、右振動測點位置水平方向上的相位相差在180°左右。

系統16 800 r/min和21 600 r/min峰值轉速對應振型分別為單獨轉子或靜子系統的振動。其中16 800 r/min峰值轉速對應振型主要表現為機匣振動；21 600 r/min峰值轉速對應振型主要表現為動力傳動軸轉子組件的彎曲振動。

4 試驗驗證

4.1 試驗測試裝置及方案

為了驗證分析的準確性，開展了動力傳動軸轉子組件動力特性試驗。試驗采用電機加增速箱的形式驅動動力傳動軸，動力傳動軸通過螺栓、膜片聯軸器與法蘭盤連接，將增速箱輸入的轉速、功率傳遞給與法蘭盤花鍵連接的輸出錐齒輪。為了測試系統的振動情況，在減速器機匣的左、右輸入級端蓋上端分別安裝三向振動傳感器，用于測試輸入端的軸向、垂直、水平方向振動，詳細試驗裝置及測試方案如圖6所示。

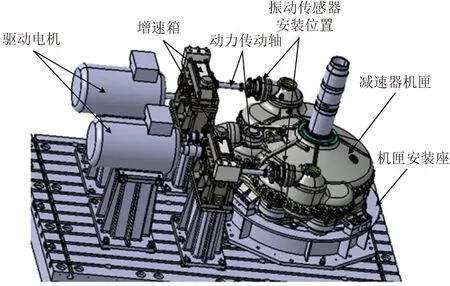
圖6 試驗裝置及測試方案Fig.6 Test device and test scheme

4.2 試驗結果分析

試驗從0 r/min轉速上推到了24 000 r/min，對右側振動傳感器采集的振動試驗數據進行頻譜分析，各方向上振動速度響應-頻率曲線如圖7所示，試驗中出現的峰值轉速與分析得到的峰值轉速對比如表1所示。

表1 峰值轉速對比Table 1 Comparison of peak speed

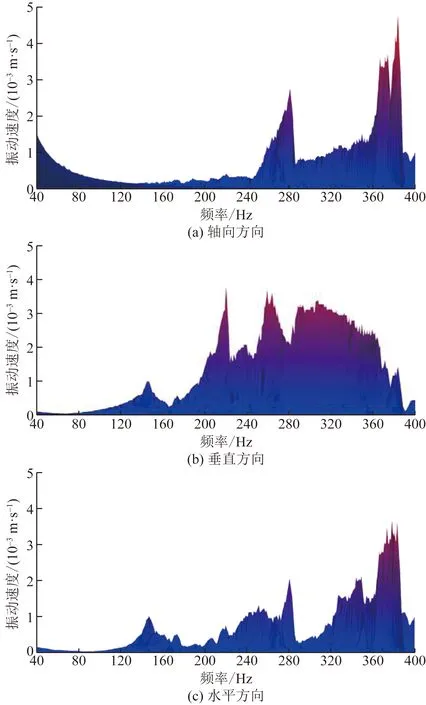
圖7 不同方向振動速度響應-頻率曲線Fig.7 Velocity response-frequency curve at different vibrations

試驗過程中出現5個峰值轉速，轉速分別為8 500、12 600、15 600、18 600和22 800 r/min。

試驗峰值轉速與計算峰值轉速結果的差異在10%以內。

系統在12 600 r/min和15 600 r/min轉速(對應系統耦合振型)時的振動響應與22 800 r/min轉速(對應單獨轉子振型)時的振動響應基本相當。

試驗中出現了8 500 r/min峰值轉速，其振動響應較小且主要表現為水平和垂直方向上的振動，推測該峰值轉速對應的振型可能為動力傳動軸轉子組件的扭轉振型，由于計算時約束了動力傳動軸轉子組件扭轉方向的位移，造成該峰值轉速在計算結果中未能出現。

為進一步驗證分析中出現的耦合振型，繪制了左、右振動測點在試驗峰值轉速12 600 r/min和15 600 r/min處振動響應時域圖，如圖8所示。可以看出，12 600 r/min峰值轉速下，左、右振動測點垂直方向振動響應相位相差180°；15 600 r/min峰值轉速下，左、右振動測點水平方向振動響應相位相差180°，這與計算得到的耦合振型中左、右振動測點振動響應相位關系相一致，間接說明計算獲得的這兩階耦合振型與試驗中共振振型基本一致。

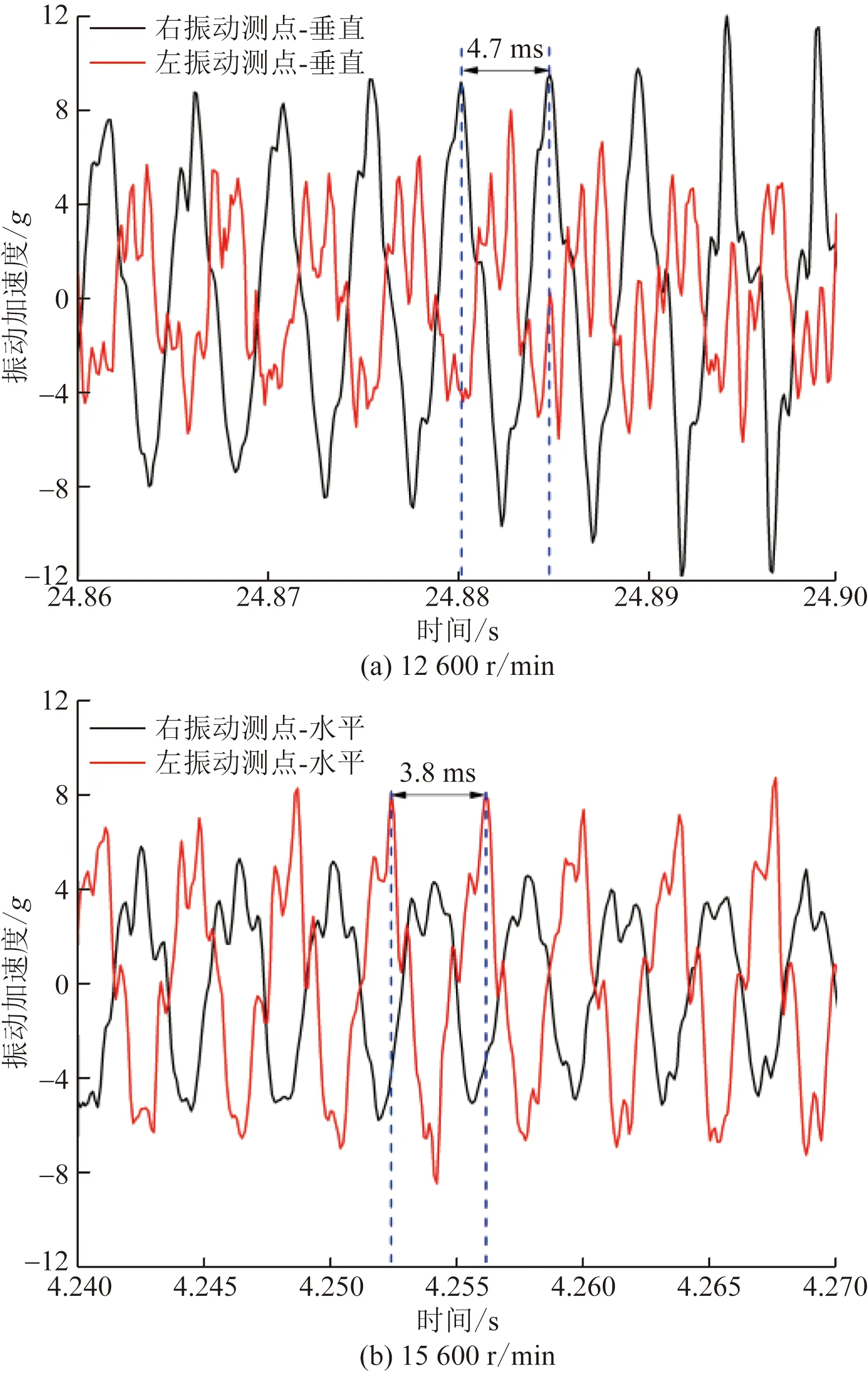
g為重力加速度圖8 12 600 r/min和15 600 r/min峰值轉速左、右振動測點水平方向時域圖Fig.8 Time domain diagram of vertical direction of left and right vibration measuring points at 12 600 r/min and 15 600 r/min peak speed

5 結論

通過對某型動力傳動軸-減速器機匣系統開展耦合振動分析和試驗研究，獲得主要結論如下。

(1)采用耦合振動分析得到的動力傳動軸-機匣系統動力特性與試驗情況吻合，計算精度在10%以內。

(2)轉靜子系統耦合振動與單獨轉子或靜子系統振動具有同等的危害性，應盡量避免工作轉速范圍內的系統耦合振動。

(3)系統耦合振動分析除了可以獲得單獨組件系統振動特性以外，還可以得到系統的耦合振動特性，更全面地指導發動機傳動系統的動力學設計。