顆粒形狀對砂性土宏細觀力學性質的影響

薛明華，陳圣仟 ，楊世文

(1.濟南市勘察測繪研究院，濟南 250101；2.貴州省建筑設計研究院有限責任公司，貴陽 550000)

砂性土(無黏聚力)是由大量土顆粒構成的多體相互作用體系[1]。球形度(form or sphericity)、圓滑度/棱角度(roundness or angularity)、粗糙度(roughness)從3個不同尺度描述了顆粒的形態特征[2-3]，被認為是顆粒形狀量化的基本指標[4]，用于評價顆粒的形狀。另外，還衍生出諸如凹凸度(non-convexity)、長寬比(aspect ratio)等[5]另外一些顆粒形狀評價指標。顆粒形狀會對砂性土的宏觀性質產生影響，如相對密實度、滲透特性、壓縮特性、剪切強度及變形等[2-10]。而宏觀上展現的力學特性本質上是細觀尺度(顆粒層面)顆粒間相互作用的累積[4,11]。對于顆粒形狀與砂性土宏觀力學特性之間的關系，研究人員開展過大量的室內試驗或數值模擬研究工作。試驗研究認為，幾乎所有砂性土的宏觀力學特性都會受到顆粒形狀的影響[2-4,11]。比如，顆粒的形狀會影響砂性土的極限孔隙比(相對密實度)，多棱角、表面粗糙和球形度低的顆粒堆積體具有較大的極限孔隙比區間長度，相反，較光滑球形顆粒堆積體的極限孔隙比區間長度較小[2,12-14]。在三軸壓縮試驗、直剪試驗中，相同密實度條件下，多棱角的砂性土比表面圓滑的砂性土具有較大的強度，且在峰值應力前具有較大變形模量[9,13]。當試樣體積變形恒定時，表面圓滑的砂較表面多棱角的砂穩定性差，強度低[15]。臨界狀態下砂性土的內摩擦角、臨界狀態線的斜率、峰值內摩擦角以及峰值應力前砂性土的變形模量均隨砂粒棱角度的增加而增加[9,16]。

多數室內或數值試驗的研究闡明了不同顆粒形狀會影響砂性土的強度和變形特性，但顆粒形狀對砂性土強度和變形特性的影響機理則鮮有研究。室內試驗具有明顯的局限性，如顆粒的粗糙度、棱角度和球形度對砂性土宏觀力學性質的影響很難做到實際意義上的分離[4,9,17]。制備由規則形狀的顆粒構成的試樣無疑脫離了天然砂性土中顆粒隨機不規則形狀的特性，且放大了顆粒形狀的影響。在這種情況下，諸多學者對顆粒形狀與砂性土力學特性的關系持不同意見，除了顆粒的球形度、圓滑度和粗糙度與砂性土力學特性的基本認識以外，有人認為顆粒形狀對砂性土剪切強度的影響甚微[18]，有人指出顆粒形狀是否對砂性土剪切強度產生影響尚不清楚[2]。

在此基礎上，現通過室內直剪試驗及其離散元模擬試驗探索顆粒形狀與砂性土力學特性，特別是強度與變形特性。研究對象是較為常見的砂性土，其顆粒為隨機不規則形狀，且在相同的試驗條件下設計基于圓形顆粒的對比試驗。

1 直剪試驗

直剪試驗的試樣為天然硅質粗砂，其級配曲線如圖1所示，不均勻系數為1.44。試樣平均粒徑為0.9 mm，密度為2.5 g/cm3，最大孔隙比1.076，最小孔隙比0.67，L/d50≈44>40且L/dmax≈18>15(L為試樣的最小尺寸，d50為平均顆粒粒徑，dmax為最大顆粒粒徑)。根據文獻[19-20]，試樣的尺寸效應很小。

剪切盒總尺寸為60 mm×60 mm×43 mm(長×寬×高)，包括上下兩盒。剪切過程采用應變控制式，剪切速率可在0.001～2 mm/min范圍內自由調節，上盒固定，由電機推動下盒剪切，垂直壓力通過杠桿懸掛載荷砝碼施加。試驗時，垂直和水平位移分別通過兩個千分位移表讀取，剪切力通過水平應力環采集，精度達±2.2 N。

制樣時按照50%的相對密實度(中密)換算試樣的質量，分層擊實，最后平整試樣的上表面，以較慢的剪速(約0.05 mm/min)在3種法向應力(22、50和100 kPa)下剪切。對應每種法向應力進行3個試樣剪切，當2次試驗結果差異很大時增加剪切試樣進行剪切試驗，每種法向應力下試驗結果取3次試驗的算術平均值。

2 模擬試驗

2.1 粒徑不同、細觀結構相同試樣生成方法

采用二維顆粒流離散元分析程序(particle flow code，PFC)模擬直剪試驗。模擬直剪試驗的理論基礎參見文獻[20]。模擬直剪試驗的對象可以是具有不同長寬比的橢圓形顆粒[21]、邊數可控制的多邊形顆粒[22]，還可以是通過顆粒自動填充(computerized particle analysis,CPA)形成的任意形狀的顆粒[23]。由于天然顆粒形狀的復雜性，要實現模擬試樣中顆粒的形狀與實際的完全相同，現有的技術是做不到的。然而，即使在顆粒形狀上存在差異，砂性土在直剪試驗中表現的力學特性還是可以被模擬試驗準確的再現，以至于追求顆粒形狀的完美匹配顯得沒有必要[7]。

劉清秉等[24]、Ye[25]通過比較樣本容量為25、50和100的顆粒的形狀統計指標，指出砂性土的某些顆粒形狀量化指標受樣本容量影響較小。據此，從直剪試驗的試樣中任意選取了25個砂粒(圖2)，基于顆粒的數字圖像處理技術[5]，獲取顆粒的輪廓后，采用CPA填充技術在PFC中生成目標形狀顆粒(圖3)。隨后按照直剪試驗試樣的尺寸和級配曲線(圖1)生成不規則形狀的試樣。為進行對比性分析，采用等體積替換法[25]，將不規則的顆粒等體積的替換為圓形顆粒。為方便表述，稱圓形顆粒試樣為試樣一，不規則形狀顆粒試樣為試樣二。由圖1可看出替換后試樣的級配幾乎沒變。

圖2 電鏡下的砂粒Fig.2 Sand under the electron microscope

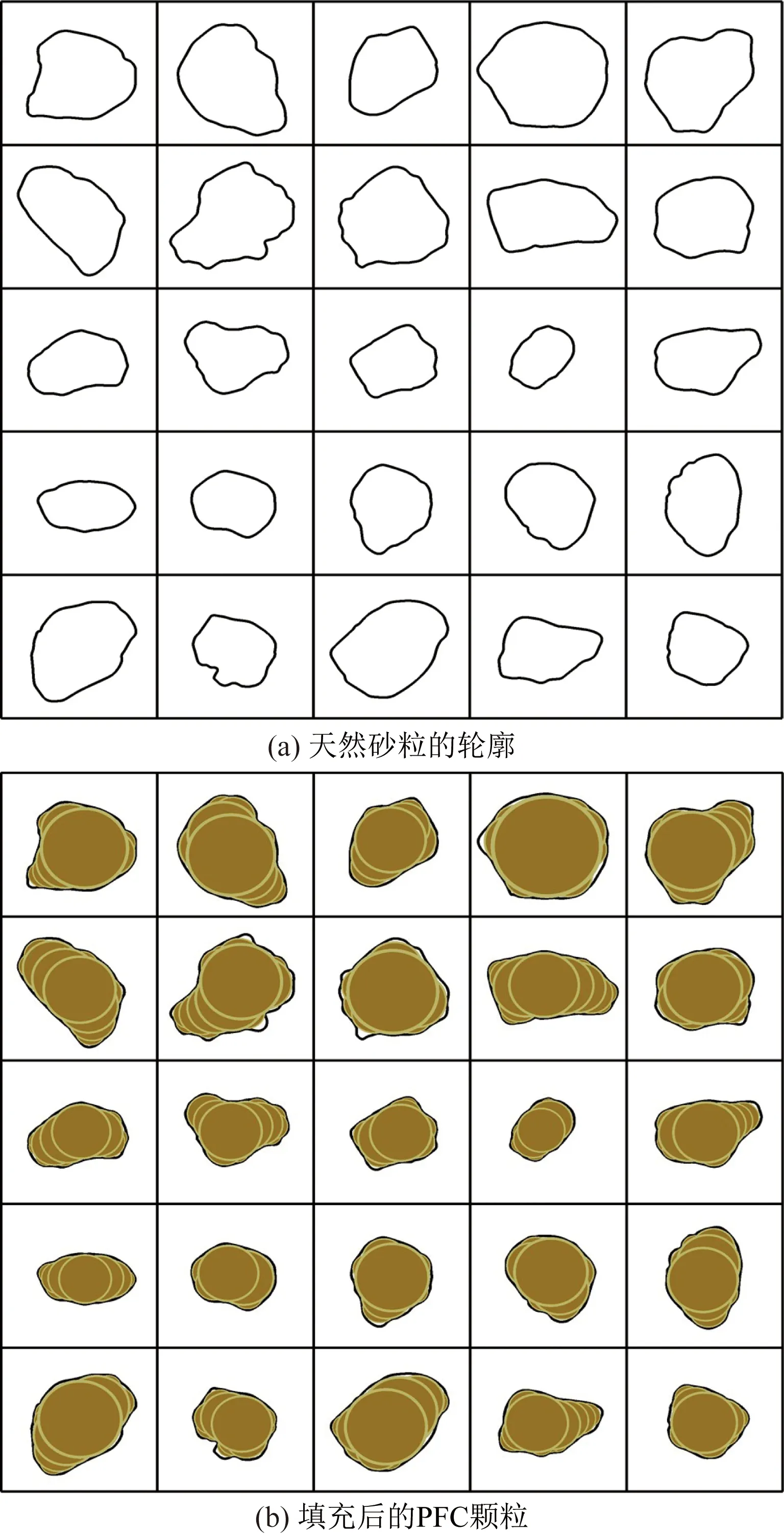
圖3 CPA填充技術生成的顆粒Fig.3 Particles generated by CPA filling technology

顆粒在沒有摩擦作用時可以堆積成致密的試樣，而在較大的摩擦作用時可以堆積成非常松散的試樣[26]。在二維模擬試驗中必須確定試樣的相對密實度，因為顆粒材料的強度和變形性質受砂性土的相對密實度的影響，而顆粒的形狀會影響砂性土的極限孔隙比(相對密實度)[2]。通過足夠多數量的顆粒即可確定砂性土的極限孔隙率[20]，試樣一最小孔隙率為0.098，最大孔隙率為0.188，試樣二最小孔隙率為0.076，最大孔隙率為0.142。試樣一的極限孔隙比區間長度比試樣二的大且試樣二最大孔隙比比試樣一的小，上述特征符合具有較低的球形度、較高的棱角度和粗糙的表面的砂礫土相比于圓形砂礫土應有較大的極限孔隙比差值的結論[13-14]。基于此，為了與室內試驗對應，采用50%的相對密度制成試樣以備剪切。

由于試樣為硅質砂，且應力水平相對較小(不超過400 kPa)，因此不考慮顆粒破碎對試驗結果造成的影響。且認為粒間接觸剛度不隨接觸力的增加而增加，可以采用線性接觸模型代替赫茲接觸模型。考慮到采用圓形顆粒試樣在模擬直剪試驗時顆粒的轉動應該受到限制，因此，粒間接觸模型采用抗旋轉的線性接觸模型[6]。通過顆粒和接觸處設置阻尼以保持剪切過程在準靜態的情況下進行。模擬直剪試驗采用恒定的剪切速度進行剪切(0.05 mm/s)，至剪位移達到10 mm(剪應變約為16%)時停止。

通過反向擬合室內試驗中得到的應力-應變曲線校對模擬試驗中的細觀參數。考慮到細觀參數與砂性土的極限孔隙率的相互影響，反復調試了細觀參數，最終細觀參數見表1和表2。砂性土的剪切強度或變形會因顆粒空間分布的不同而在一定范圍內波動[20]。為此，模擬直剪試驗采用3種不同隨機數構建模型，分別進行平行試驗，取其平均值作為模擬直剪試驗的結果并計算其標準差。

表1 接觸的細觀參數Table 1 Meso-parameters of contact

表2 邊界墻和顆粒的細觀參數Table 2 Mesoscopic parameters of boundary walls and particles

3 試驗結果及討論

3.1 標定結果

直剪試驗及其模擬試驗的剪應力-剪位移曲線、法向位移-剪位移曲線見圖4和圖5(帶誤差線的均為模擬直剪試驗的結果。基于建模方法和細觀參數，模擬直剪試驗很好地再現了直剪試驗的剪切過程。剪切至8～10 mm時，試樣的體積基本上處于恒定的狀態，即臨界狀態[17]。通過直剪試驗和模擬直剪試驗獲得的臨界摩擦角分別為33.9°和32.3°。基于剪切后的試樣所做的6組休止角試驗，獲得試樣休止角為31.8°±0.6°。直剪試驗和模擬直剪試驗獲得的臨界摩擦角與試樣休止角的平均值分別相差2.1°和0.5°。Herle等[27]曾指出干砂臨界摩擦角φcv與其休止角非常接近，相差約±0.5°，并提出了用干砂休止角估算其臨界摩擦角的方法。Guo等[16]統計的磨圓度(roundness)較好的渥太華標準砂(Ottawa standard sand)休止角為31°。因此，直剪試驗及其模擬直剪試驗均具有很好的可信度。

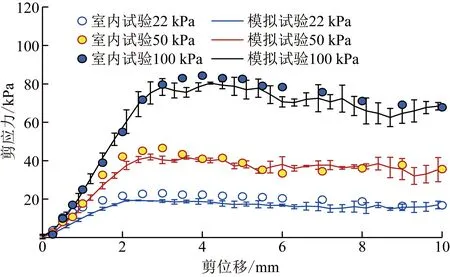
圖4 直剪試驗及其模擬直剪試驗的剪應力-剪位移曲線Fig.4 The shear stress-shear displacement curve of the direct shear test and its simulated direct shear test

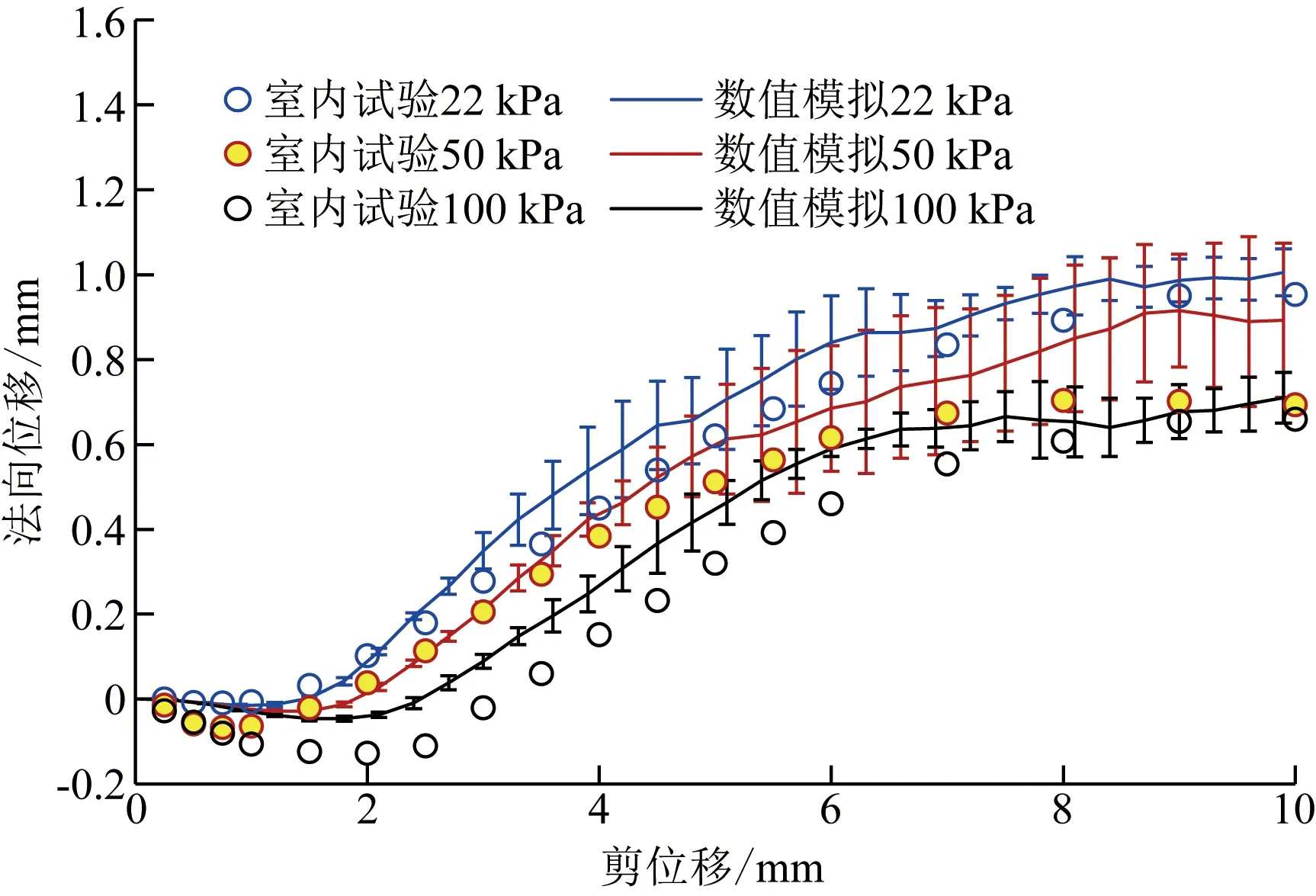
圖5 直剪試驗及其模擬直剪試驗的法向位移-剪位移曲線Fig.5 Normal displacement-shear displacement curve of direct shear test and its simulated direct shear test

3.2 顆粒形狀對試樣宏觀力學性質的影響

試樣二與試樣一相比，除了顆粒形狀上的差別外，試樣的相對密實度、顆粒級配、試驗條件以及顆粒的數量均是相同的。為了研究法向應力對研究結果的影響，除了采用22、50和100 kPa法向應力外，還增加了法向應力為200、300和400 kPa的模擬直剪試驗。兩種試樣均在極限孔隙率下(密實狀態和松散狀態)的進行剪切試驗。試樣密實狀態下的峰值強度取剪應力能達到的最大值，臨界值強度取8～10 mm段的剪應力平均值并計算其標準差，試樣松散狀態下的強度取剪應力能達到的最大值。

按照Mohr-Coulomb準則進行直線擬合，得到不同法向應力下密實狀態的兩種試樣的峰值強度和臨界值強度(圖6和圖7)。結果表明，當法向應力小于200 kPa時，試樣一峰值強度大于試樣二；當法向應力大于200 kPa時，試樣一峰值強度小于試樣二。隨著法向應力增大，試樣二表現出較高的剪切強度。試樣二臨界值強度以及臨界摩擦角均略比試樣一的大，但差別甚小(試樣一和試樣二臨界摩擦角分別為32.6°和33°)。有文獻報道稱不規則的顆粒形狀會增加砂性土的剪切強度，例如，Kandasami等[4]在300 kPa圍壓下分別對由石英砂和玻璃球組成的砂性土做了空心圓柱體抗扭試驗，得出石英砂不規則的形狀增加了試樣的剪切強度。然而,Ng[18]在100 kPa圍壓下基于4種具有不同長細比的橢球體試樣進行三軸壓縮試驗，其結論表明顆粒形狀對砂性土的峰值和臨界摩擦角影響很小。Cho等[2]表示顆粒形狀對砂性土力學特性的影響機理仍不清楚。在顆粒形狀影響砂性土極限孔隙比(相對密實度)的情況下，諸多文獻忽略了對試樣相對密實度的校核[2]，這也是文獻[10]中沒有注意到的。他們的結論中沒有提及顆粒形狀對剪切強度大小產生明顯影響的條件。模擬直剪試驗結果表明，對于密實狀態的砂性土，只有在較高的應力水平下顆粒不規則形狀才能明顯增加砂性土的剪切峰值強度，在較低的法向應力時其剪切峰值強度反而比規則圓形砂性土的低。在文中整個法向應力范圍內，試樣二臨界值強度以及臨界摩擦角均略比試樣一的大，但差別很小，可以認為顆粒不規則形狀沒有明顯增加砂性土的臨界值強度。

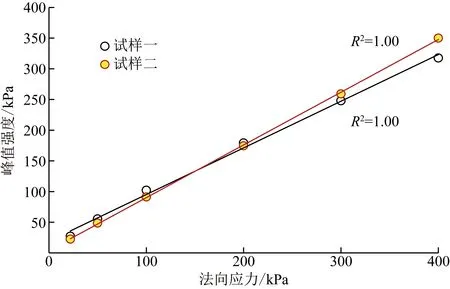
圖6 在密實狀態下的峰值強度Fig.6 Peak intensity in the dense state

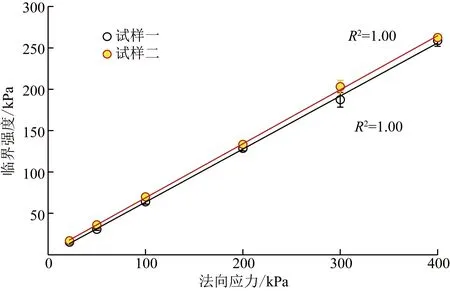
圖7 在密實狀態下的臨界值強度Fig.7 Critical value strength in the dense state

圖8為松散狀態下的兩種試樣在不同法向應力時的剪切強度。可以看出，試樣二的內摩擦角明顯比試樣一大，然在較低法向應力時，極值強度上的差別幾乎可以忽略，隨著法向應力的增加，兩種試樣極值強度差成比例增加。

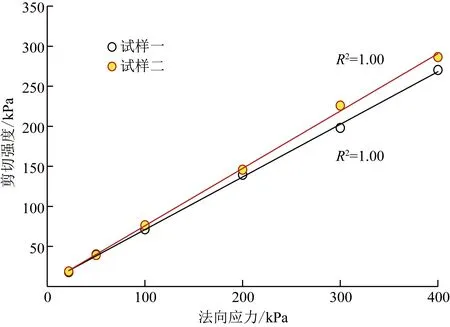
圖8 在松散狀態下的極值強度Fig.8 The extreme strength in loose state

4 顆粒形狀對砂性土力學性質的影響機理

4.1 直剪試驗中試樣應力的變化

自開始剪切至出現峰值強度的過程中，顆粒間接觸力方向由開始的隨機分布[圖9(a)]轉變為定向分布[圖9(b)]，即形成柱狀力鏈(column)。當達到峰值強度時，剪切面上柱狀力鏈Fi方向近似相等，令其與法向夾角為θi，則法向應力N、剪應力T與Fi之間的關系式為

(1)

式(1)中：n為剪切面[圖9(b)中虛線]上柱狀力鏈的個數。剪切面上n個Fi矢量和可以用一個綜合的矢量F表示，其與法向夾角為θ(反算或模擬直剪試驗中直接獲得)，則法向應力N、剪應力T與F的關系式為

(2)

剪應力T等于0時，θ等于0，意味著沒剪切前，剪切面上綜合矢量F方向是豎直的。剪應力逐漸增大到峰值過程中，θ亦逐漸增大到極值。一方面，顆粒緩慢移動，在剪切盒對角線方向上顆粒間的接觸越來越多，到峰值處最明顯；另一方面，對角線方向上顆粒間的接觸力逐漸增大，而其他方向上的接觸力逐漸向剪切盒對角線方向上偏轉、減小或消失 [圖9(a)、圖9(b)的插圖]。剪應力出現峰值后，對角線方向上接觸力的增大使其法向分量超過加壓板的壓力，從而使剪切面以上的顆粒連同加壓板反向運動，同時剪切面附近形成的柱狀力鏈繞其中心順時針轉動[22]，θ又開始減小，根據式(1)、式(2)可知，剪應力T亦開始減小，剪切帶區域空隙增大，試樣體積膨脹。當θi過小時，柱狀力鏈會發生潰曲，新的柱狀力鏈又會生成，剪應力逐漸進入到臨界值狀態[圖9(c)]。

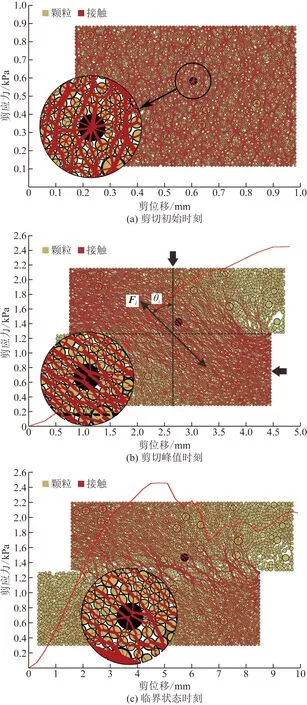
圖9 密實試樣一剪切過程中不同階段顆粒間接觸力狀態(法向應力300 kPa)Fig.9 The state of the contact force between particles at different stages during the shearing process of the compact specimen (normal stress 300 kPa)

根據式(2)中剪應力T、法向應力N和綜合矢量F與N夾角θ的關系，提出一種新的本構關系如圖10所示，剪應力T的大小可根據參數N和θ做出預測。根據Rowe剪脹理論，等粒徑的圓形顆粒極密排列情況下，綜合矢量F與法向夾角可達60°，因此0°≤θ≤60°。兩種試樣表明，剪切過程中θ的變化受顆粒形狀的影響，剪應力達到峰值和臨界值時的θ分別為θp和θc。

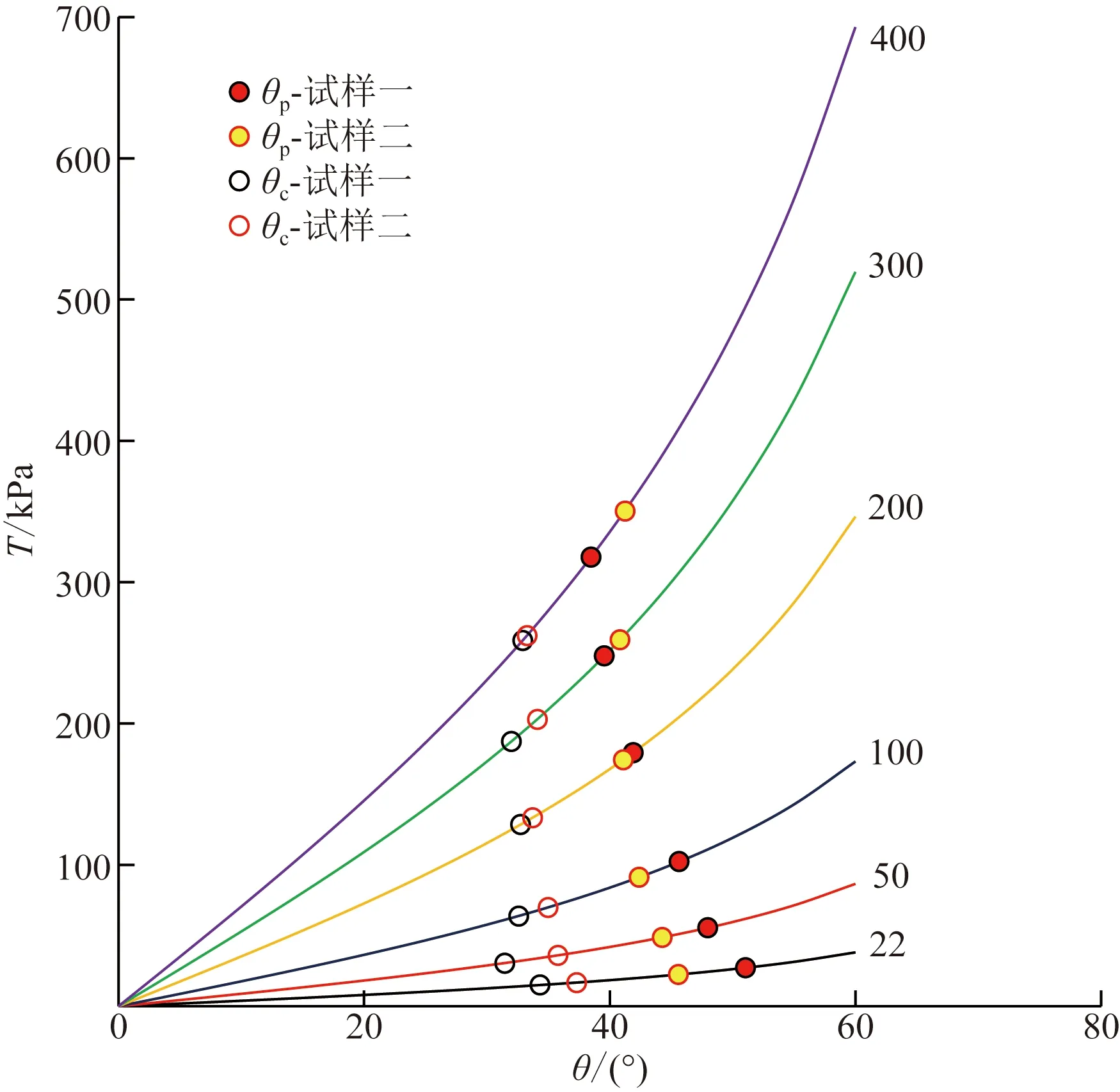
圖10 不同法向應力下剪應力T和夾角θ的關系Fig.10 The relationship between the angle θ and the shear stress T under different normal stresses

兩種試樣的Tp-θp(Tp為峰值剪應力)曲線均較好呈現雙曲線形態，低法向應力時，試樣一θp偏大而試樣二偏小，高應力時相反，θp均落于40°～50°范圍，甚至試樣二的θp區間更小。而對于Tc-θc(Tc為臨界剪應力)曲線而言，試樣二依然呈現出較好的雙曲線形態，而試樣一在低應力時離散性較大，試樣二總體上具有較大的θc，且在高應力情況下更明顯，θc傾向于30°～40°范圍。正如文獻[19]中所述，密實試樣的θp、θc應介于30°～60°。

4.2 剪脹作用的影響

Rowe[28]認為顆粒間的摩擦作用和剪脹作用是剛性顆粒材料剪切強度的主要來源，提出應力剪脹關系式為

(3)

式(3)中：σ11、σ22為試樣所受的最大和最小主應力，Pa；dεv為體積應變增量；dε1為剪切方向上的應變增量；φu為顆粒表面的摩擦因數。式(3)說明，對于同一個試樣，其應力比R=σ11/σ22會與剪脹因子D=1-dεv/dε1同步變化，當應力比達到峰值時，剪脹因子會出現最大值。

直剪試驗中，有關剪脹角ψ的表達式為

(4)

式(4)中：dεx、dεy分別為試樣在剪切方向和法向上的變形增量；tanψ實質上是法向位移-剪位移曲線的斜率。模擬直剪試驗結果表明，剪應力峰值所對應的tanψ總是最大的，即最大剪脹角ψmax，不同法向應力下兩種試樣的ψmax見圖11。Bolton[29]在砂土的三軸壓縮試驗中得出最大剪脹角ψmax與峰值摩擦角φp的關系式為

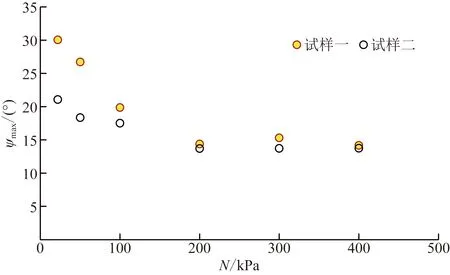
圖11 不同法向應力下兩種試樣的ψmaxFig.11 Two specimens under different normal stresses ψmax

φp=0.8ψmax+φc

(5)

式(5)中：φc為砂土的臨界摩擦角。

圖12為兩種試樣的θp、θc與ψmax的關系曲線，虛線為文獻[16]基于Ottawa標準砂做的三軸壓縮試驗中的結果。雖然直剪試驗與三軸試驗關于參數的定義有所區別，但是它們的物理意義一樣，模擬直剪試驗結果表明，θp、θc與ψmax同樣服從很好的線性關系，與文獻[16]的三軸試驗結果非常吻合。

當法向應力較小時(22 kPa和50 kPa)，在剪應力達到峰值時，顆粒體尚未出現明顯的剪切帶，體應變不明顯，剪應變很小。根據Barton等[30]提出的不平整的巖體節理面抗剪強度理論，在剪應變較小以及法向應力較小時，剪應力T、法向應力N的關系式為

T=Ntan(θc+ψ)

(6)

由圖12可知，在低法向應力時，試樣一的峰值剪脹角比試樣二的大，而由圖7可知，兩種試樣的θc幾乎無差別，因而試樣一在低法向應力下峰值強度較大主要原因是試樣一的剪脹角比試樣二的大些。

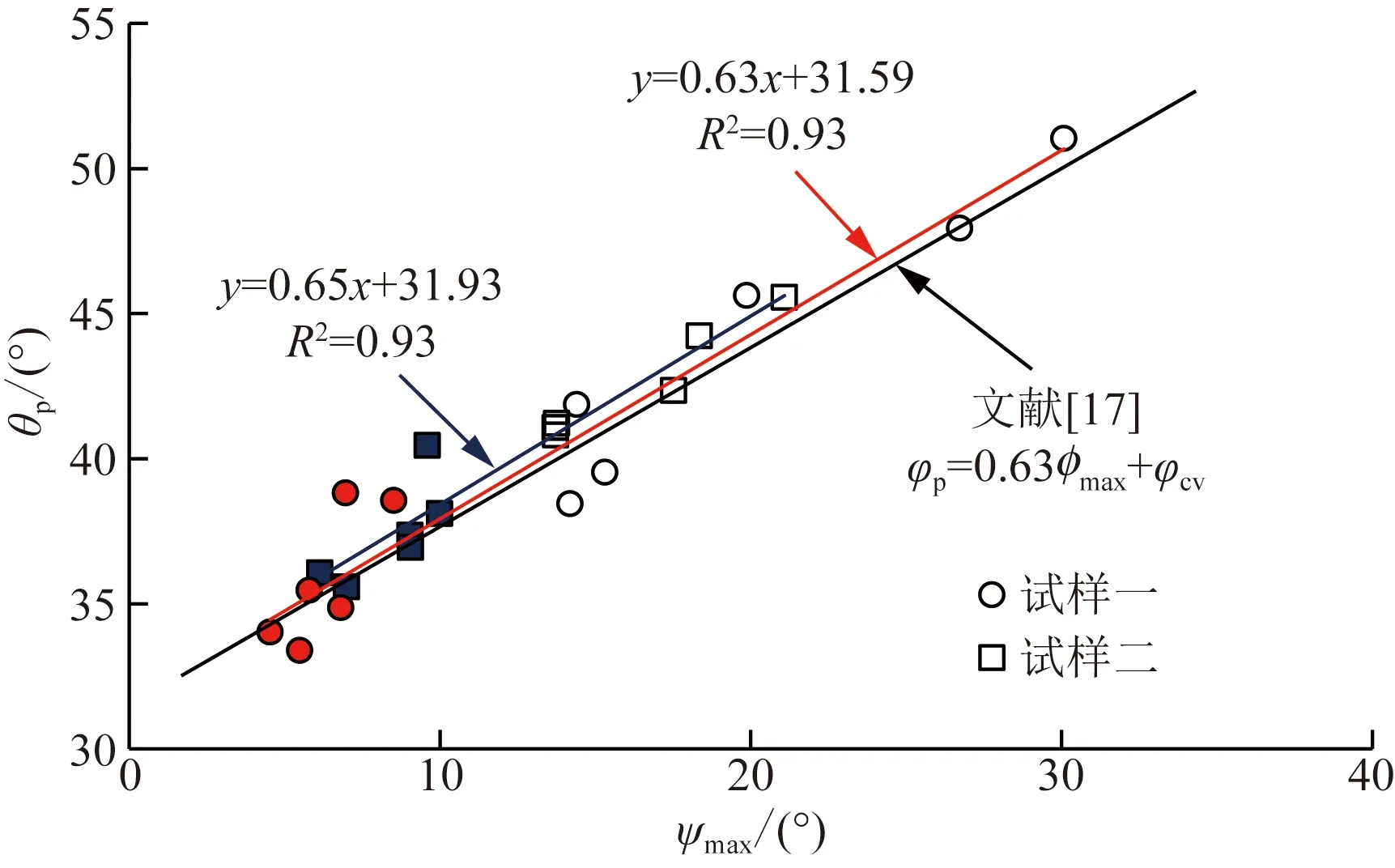
文獻[17]公式中，φp和φcv分別為三軸壓縮試驗中試樣的峰值及臨界摩擦角，φmax為最大剪脹角圖12 兩種試樣θp、θc與ψmax的關系Fig.12 The relationship between two samples θp，θc and ψmax

圖13為圓形顆粒體和橢圓形顆粒體剪脹變形圖解，圓形顆粒與橢圓形顆粒的面積相同，假設顆粒間均未發生相對滑動，則柱狀顆粒體會發生轉動，當發生相同剪切位移時(dεx=1.79)，圓形顆粒體的位移增量(dεy=1.03)要比橢圓形顆粒體的(dεy=0.74)大些，按照剪脹角的定義[式(4)]不難看出圓形試樣剪切時具有較大的剪脹角的原因。當法向應力較高(300 kPa和400 kPa)時，剪應力達到峰值時發生了較大的剪切位移，兩種試樣的峰值剪脹角ψmax也趨于相同，此時式(6)不再適用。文獻[17]認為多棱角的顆粒之間可形成鎖定(interparticle locking)結構，增加了顆粒體的剪脹性，因而增加了顆粒體的峰值摩擦角φp。

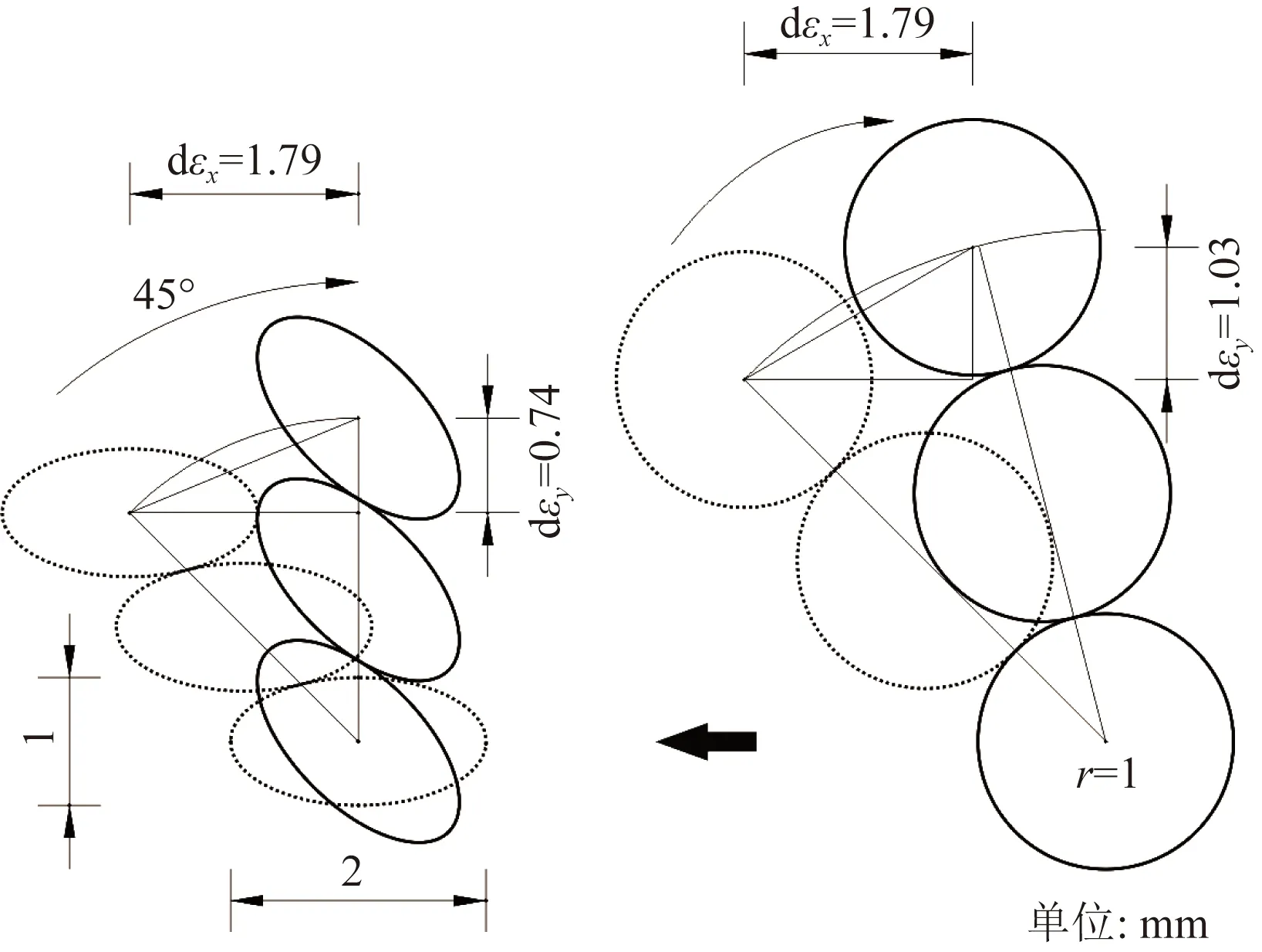
圖13 橢圓形與圓形顆粒體變形圖解Fig.13 Illustration of deformation of ellipse and round particles

4.3 顆粒間摩擦作用的影響

模擬直剪試驗表明，受摩擦作用影響的顆粒間的滑動和滾動及其相互轉化機制一定程度上控制著顆粒體的宏觀強度，隨著顆粒表面摩擦系數的增高，顆粒體的宏觀強度呈非比例增高[31]。當抗旋轉阻力矩系數小于顆粒表面摩擦因數時，顆粒體強度會因其增大而增大，當抗旋轉阻力矩系數超過顆粒表面摩擦因數時，顆粒體強度的增加不再明顯[32]。為此，對兩種試樣在100 kPa法向應力下，顆粒表面摩擦因數在0～1變化時，密實狀態顆粒體的強度(峰值強度、臨界值強度)進行了探討，在設定一個顆粒表面摩擦因數時，同時給予一個相同的抗旋轉組力矩系數，試驗結果見圖14。

在沒有摩擦的情況下，兩種試樣的強度值極低，說明摩擦作用是無黏性粗顆粒體(相對于黏土或粉土而言的砂土或粗粒土等)強度的主要來源之一。當摩擦因數為零時，試樣一中圓形顆粒間接觸力必然通過圓心，這樣在沒有切向力的情況下，圓形顆粒不受彎矩，因而不會發生轉動；相反，試樣二顆粒的形狀是不規則的，接觸力偏離形心，顆粒受到較大的偏心距，所有顆粒均發生較大的轉動，導致試樣一最終的體積膨脹量(1.77%)遠比試樣二(0.38%)的大，其強度上的差異可能與此有關。另外，無摩擦作用時，兩種試樣內顆粒間接觸力分布均勻，均無明顯的應力局部化現象(即無強弱力鏈)。

Skinner[33]曾指出臨界狀態摩擦角幾乎不受顆粒間摩擦作用強弱的影響，然而Abriak[34]通過一系列的雙軸試驗反駁了Skinner的結論，得出當顆粒間摩擦角在0°～30°變化時，相應的臨界狀態摩擦角從20°增加到26°。模擬直剪試驗表明(圖14)，兩種試樣的峰值強度和臨界值強度均隨著顆粒表面摩擦因數和抗旋轉阻力矩系數的升高而非比例升高，這與文獻[1]中結論類似。在較低的摩擦作用下，試樣二的峰值強度比試樣一的低。當顆粒表面摩擦因數較大時，試樣二的峰值強度更高，由此可以得出，顆粒間較大的摩擦作用，可使得試樣二峰值強度較試樣一高。當顆粒間摩擦作用較弱時，臨界狀態剪切強度受其影響明顯，較強時影響不明顯。但是，摩擦作用的強弱不會改變不同形狀顆粒體臨界摩擦角似乎相等這一特征。

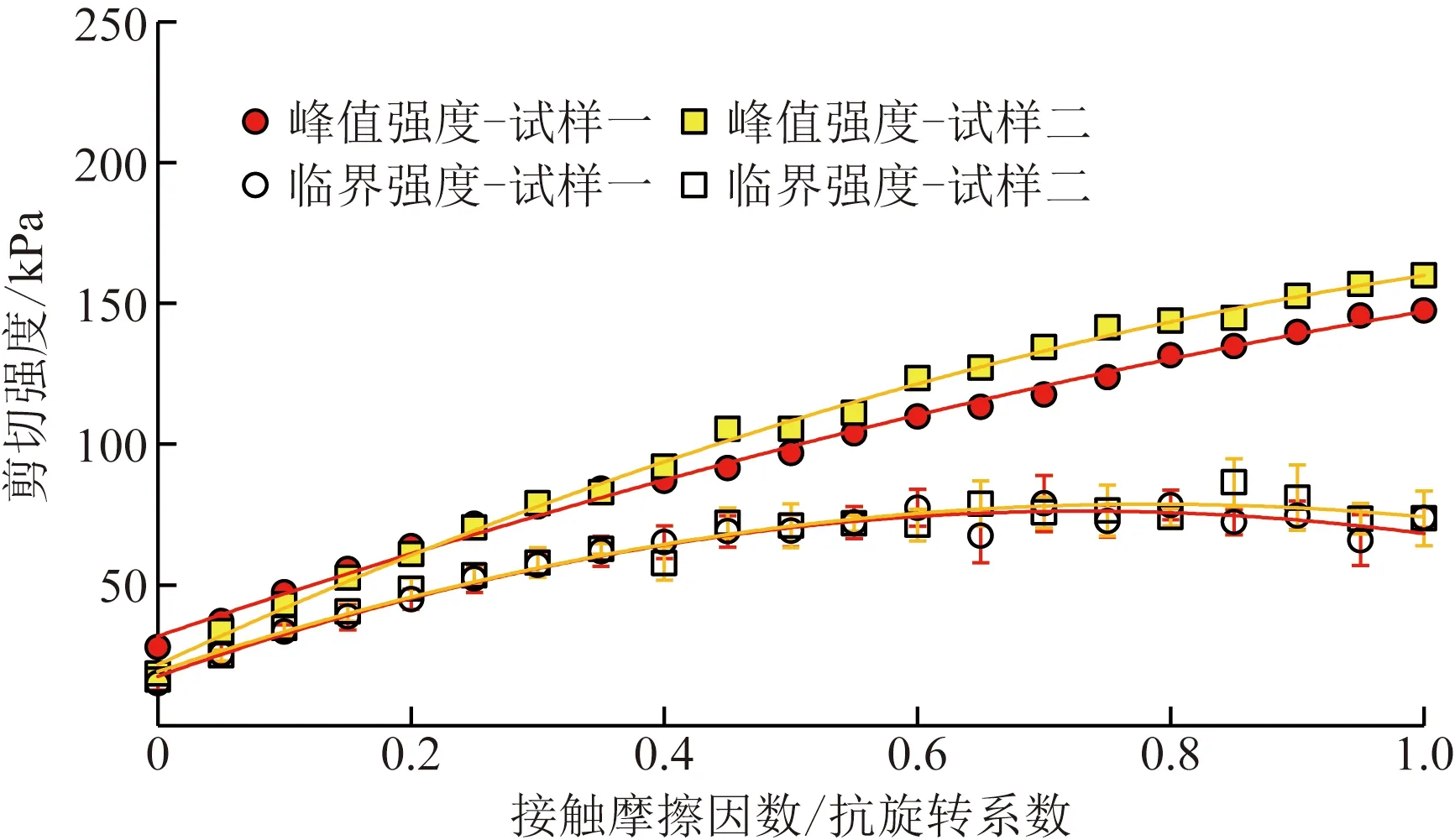
圖14 100 kPa法向應力下剪切強度與顆粒表面摩擦因數和抗旋轉阻力矩系數比值的關系Fig.14 The relationship between shear strength and the ratio of particle surface friction coefficient and moment coefficient of resistance to rotation at 100 kPa normal stress

5 結論

采用PFC中Clump模塊構建不規則形狀的顆粒并生成仿真砂樣，顆粒的形狀取自天然砂粒，一定程度上反映了砂性土中砂粒的形狀特征。通過室內直剪試驗，標定了模擬直剪試驗所需的細觀參數，嚴格地確定了不同試樣的極限孔隙率。設定不同的法向應力條件，開展了一系列的模擬直剪試驗。通過設置基于圓形顆粒的對比試驗，揭示了天然砂性土中顆粒形狀對其宏細觀力學性質的影響。定義了剪切面上顆粒間接觸力合力與法向應力的夾角參數θ，數值上其正切函數值等于剪應力T和法向應力N的比值。基于θ構造了新的本構關系式，揭示了剪應力變化的原因。基于剪脹角理論，從顆粒層面揭示了法向應力較低時不規則形狀顆粒體剪切強度較圓形試樣低的主要原因。得到如下結論。

(1)密實狀態下不規則形狀的砂粒組成的試樣較圓形顆粒試樣具有更大的峰值摩擦角和幾乎相等的臨界摩擦角；松散狀態下具有更大的內摩擦角。

(2)在較低的法向應力條件下密實不規則形狀顆粒體的剪切峰值強度比圓形顆粒體低，而在較高的法向應力條件下比圓形顆粒體高。兩者臨界值強度差別甚小。

(3)法向應力較低時不規則形狀顆粒體剪切強度較圓形試樣低的主要原因是圓形試樣具有較大剪脹角。