時(shí)間尺度上Lagrange 系統(tǒng)的Hojman 守恒量1)
張 毅 田 雪 翟相華 宋傳靜
* (蘇州科技大學(xué)土木工程學(xué)院,江蘇蘇州 215011)
? (南京理工大學(xué)理學(xué)院,南京 210094)
** (蘇州科技大學(xué)數(shù)學(xué)科學(xué)學(xué)院,江蘇蘇州 215009)
引言
力學(xué)系統(tǒng)的對(duì)稱(chēng)性與守恒律密切相關(guān).通過(guò)研究對(duì)稱(chēng)性而探索或發(fā)現(xiàn)復(fù)雜力學(xué)系統(tǒng)的守恒律,這是分析力學(xué)研究的一個(gè)重要方面[1-2].Lie 對(duì)稱(chēng)性[3-9]、Noether 對(duì)稱(chēng)性[10-20]和Mei 對(duì)稱(chēng)性[21-28]是3 種概念不同的對(duì)稱(chēng)性方法.利用對(duì)稱(chēng)性和守恒律,可以簡(jiǎn)化動(dòng)力學(xué)問(wèn)題甚至求解力學(xué)系統(tǒng)的精確解,從而更好地理解其動(dòng)力學(xué)行為.微分方程的Lie 理論最早由Lutzky[29]引入力學(xué)系統(tǒng),所得守恒量是Noether 型的.Hojman[30]由Lie 對(duì)稱(chēng)性直接導(dǎo)出一類(lèi)不屬于Noether 型的守恒量,稱(chēng)之為Hojman 守恒量[21].Hilger[31]于1990 年提出了測(cè)度鏈上的分析理論,而時(shí)間尺度作為測(cè)度鏈的特殊情形備受關(guān)注[32-34].時(shí)間尺度分析不僅是連續(xù)分析和離散分析的統(tǒng)一,而且是經(jīng)典微積分對(duì)任意時(shí)間尺度的拓廣.Bartosiewicz和Torres[35]首先開(kāi)展時(shí)間尺度上Noether 對(duì)稱(chēng)性的研究,此后關(guān)于時(shí)間尺度上Noether 定理及其證明的探討至今仍方興未艾[36-42].但是,時(shí)間尺度上Lie 對(duì)稱(chēng)性直到最近才有一些初步的研究且所得守恒量均為Noether 型的[43-46].鑒于此,本文將研究并給出由時(shí)間尺度上Lie 對(duì)稱(chēng)性直接導(dǎo)出的非Noether 型的新型守恒量.
1 時(shí)間尺度微積分
為方便讀者,這里對(duì)時(shí)間尺度微積分做一簡(jiǎn)單介紹,詳見(jiàn)文獻(xiàn)[32-33].
設(shè) T 是一個(gè)時(shí)間尺度,即實(shí)數(shù)集 R 的任意非空閉子集,如實(shí)數(shù)集 R、整數(shù)集Z、非負(fù)整數(shù)集N0或[1,3]∪N .前跳算子σ (t)=inf{s∈T:s>t} 和后跳算子 ρ (t)=sup{s∈T:s<t} 是關(guān)于時(shí)間尺度的兩個(gè)重要的量.若 σ (t)=t,稱(chēng)點(diǎn)t∈T 右稠密,σ (t)>t則右發(fā)散;若 ρ (t)=t,稱(chēng)點(diǎn)t∈T 左稠密,ρ (t)<t則左發(fā)散.相鄰點(diǎn)的位置關(guān)系在時(shí)間尺度上可用向前或向后步差函數(shù) μ (t)=σ(t)-t或 υ (t)=t-ρ(t) 描述.



2 時(shí)間尺度上運(yùn)動(dòng)微分方程
時(shí)間尺度上Lagrange 方程為[28]

3 時(shí)間尺度上Lagrange 系統(tǒng)的兩個(gè)重要關(guān)系式
本節(jié)推導(dǎo)時(shí)間尺度上Lagrange 系統(tǒng)的兩個(gè)重要關(guān)系式,它們是推導(dǎo)時(shí)間尺度上Hojman守恒量的基礎(chǔ).



式(19)和式(21)是時(shí)間尺度上Lagrange 系統(tǒng)導(dǎo)數(shù)運(yùn)算的兩個(gè)重要關(guān)系式.
4 時(shí)間尺度上Lie 對(duì)稱(chēng)性
在時(shí)間尺度上引進(jìn)無(wú)限小變換

依據(jù)微分方程在單參數(shù)Lie 變換群下的不變性,可定義時(shí)間尺度上Lagrange 系統(tǒng)的Lie 對(duì)稱(chēng)性,即
定義1.對(duì)于時(shí)間尺度上Lagrange 系統(tǒng)(5),當(dāng)且僅當(dāng)

則變換式(22)是Lie 對(duì)稱(chēng)性的.
方程(24)可寫(xiě)為
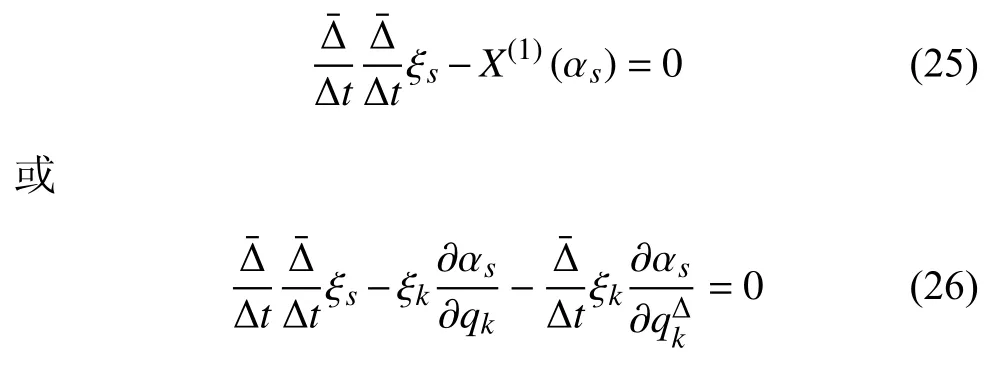
稱(chēng)方程(25)或式(26)為時(shí)間尺度上Lie 對(duì)稱(chēng)性確定方程.
5 時(shí)間尺度上Lie 對(duì)稱(chēng)性定理
由Lie 對(duì)稱(chēng)性可直接導(dǎo)出時(shí)間尺度上一類(lèi)新守恒量,即有:
定理1.對(duì)于時(shí)間尺度上Lagrange 系統(tǒng)(5),如果變換式(22)是Lie 對(duì)稱(chēng)性的,并假設(shè)所有函數(shù)對(duì)其變量的混合delta 偏導(dǎo)數(shù)連續(xù),且存在函數(shù)ψ=ψ(qs)使得
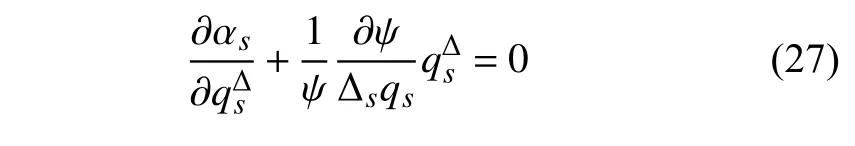
則該系統(tǒng)存在新的守恒量,形如
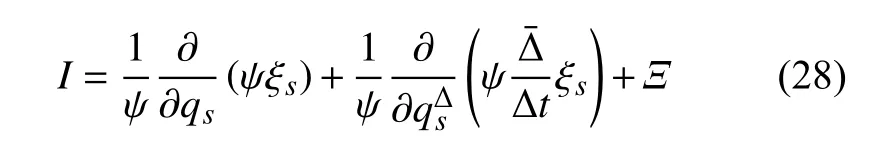
其中

證明:將式(28)按方程(6)對(duì)時(shí)間t求delta 導(dǎo)數(shù),得

根據(jù)假設(shè),所有函數(shù)對(duì)其變量的混合delta 偏導(dǎo)數(shù)連續(xù),因此函數(shù) ξs和 αs對(duì)變量qs和求delta 偏導(dǎo)數(shù)以及普通偏導(dǎo)數(shù)的次序可交換[33].利用關(guān)系式(19)和式(21),有

注意到 ψ =ψ(qs),因此有

將式(31)~ 式(33)代入式(30),得到

將確定方程(25)和式(27)代入上式,有

因此,式(28)是該系統(tǒng)的守恒量.證畢.
定理1 可稱(chēng)為時(shí)間尺度上Lagrange 系統(tǒng)的Lie 對(duì)稱(chēng)性定理.式(28)可稱(chēng)為時(shí)間尺度上Hojman守恒量,它是由Lie 對(duì)稱(chēng)性直接導(dǎo)致的.
對(duì)于任意時(shí)間尺度,守恒量(28)中函數(shù) Ξ 一般不等于零.函數(shù) Ξ 出現(xiàn)的原因在于任意時(shí)間尺度上delta 偏導(dǎo)數(shù)不同于普通偏導(dǎo)數(shù),而當(dāng)時(shí)間尺度T=R時(shí)兩者是一致的.實(shí)際上,若取 T =R,則有
因此 Ξ =0,于是定理1 退化為
定理2.對(duì)于經(jīng)典Lagrange 系統(tǒng),如果無(wú)限小變換(22)是Lie 對(duì)稱(chēng)性的,且存在函數(shù) ψ =ψ(qs) 滿(mǎn)足條件是該系統(tǒng)的守恒量.
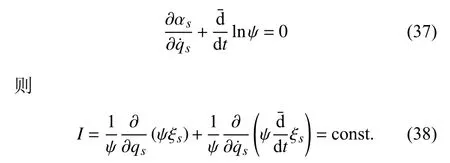
定理2 與文獻(xiàn)[30]的結(jié)果一致.
6 算例
例.設(shè)時(shí)間尺度為 T ={2m:m∈N0},研究?jī)勺杂啥萀agrange 系統(tǒng),其Lagrange 函數(shù)為
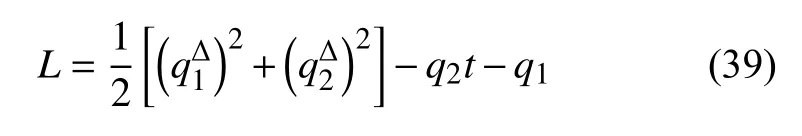
試研究該系統(tǒng)的Lie 對(duì)稱(chēng)性,并求出對(duì)應(yīng)的Hojman守恒量.
時(shí)間尺度上Lagrange 方程(5)給出

注意到,對(duì)于時(shí)間尺度上任意函數(shù)u(t),有關(guān)系
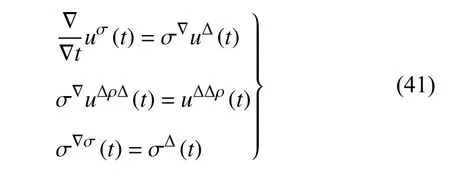
因此,方程(40)可解出
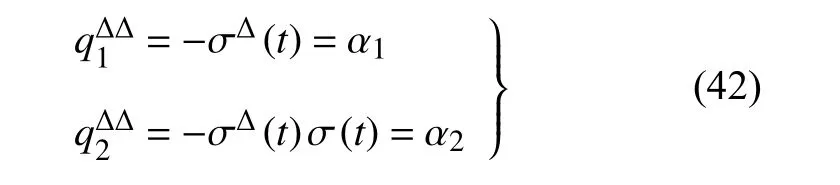
確定方程(25)給出
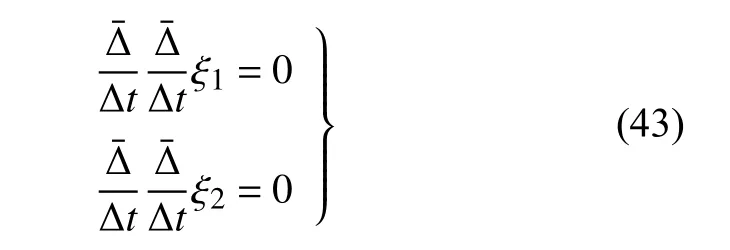
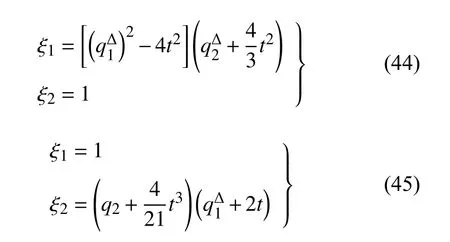
與生成元式(44)和式(45)相應(yīng)的變換是Lie 對(duì)稱(chēng)的.方程(27)給出
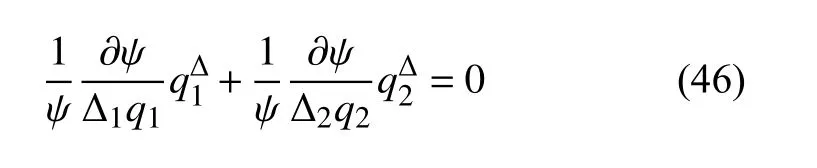
方程(46)有解

根據(jù)定理1,由式(44),式(45)和式(47),得到

這是時(shí)間尺度上Lie 對(duì)稱(chēng)性式(44)和式(45)導(dǎo)致的Hojman 守恒量.如果取初始條件為q1(1)=1,q2(1)=0 ,q1(2)=2,q2(2)=1 ,在時(shí)間尺度為T(mén)=上計(jì)算運(yùn)動(dòng)軌跡q1,q2和守恒量I1,I2的值,其結(jié)果如圖1 所示.圖1 中具體的數(shù)據(jù)如表1 所示.
表1 時(shí)間尺度 T =上 q 1,q2,I1,I2 的值Table 1 The values of q 1,q2,I1,I2 on the time scale T=
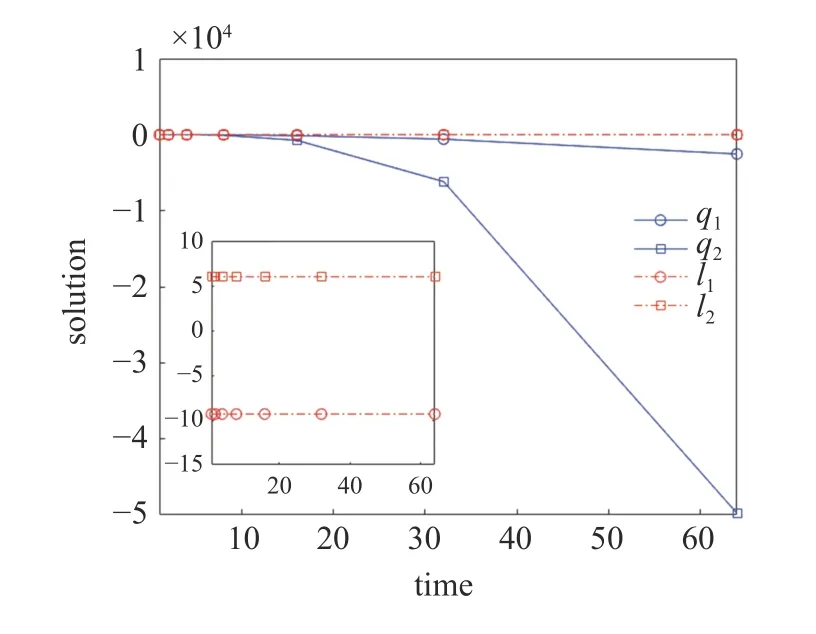
圖1 時(shí)間尺度 T = 上 q 1,q2,I1,I2 的值Fig.1 Simulations of q 1,q2,I1,I2 on the time scale T=
如取 T =hZ+,h為常 數(shù),則 σ (t)=t+h,μ (t)=h,Lie 對(duì)稱(chēng)性式(44)和式(45)成為
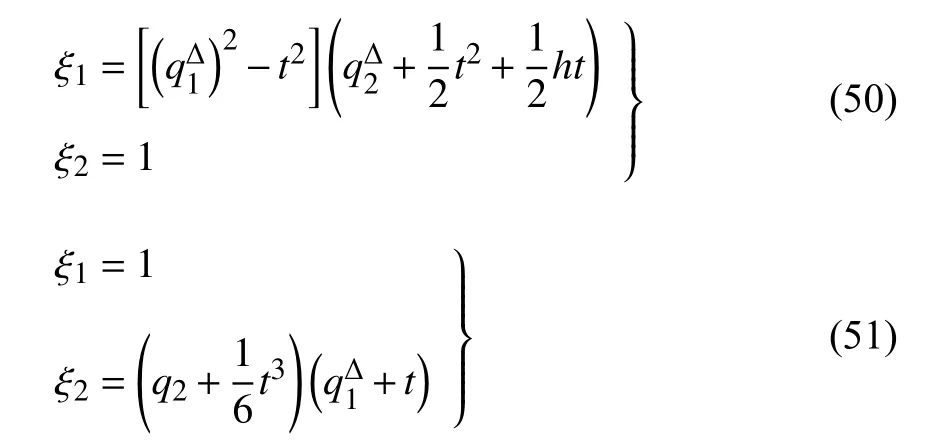
守恒量式(48)和式(49)成為
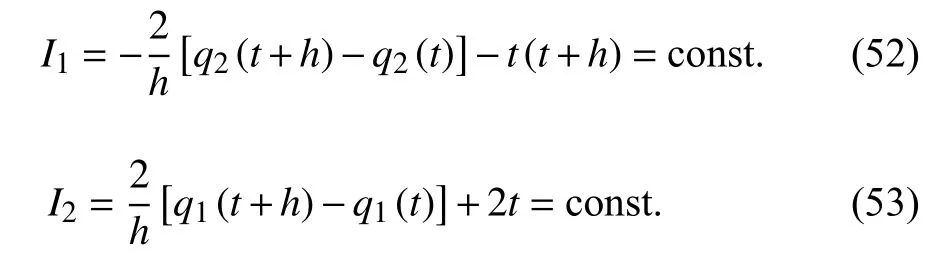
仍取上述初始條件,令h=1 ,在時(shí)間尺度為 T =Z+上計(jì)算運(yùn)動(dòng)軌跡q1,q2和守恒量I1,I2的值,其結(jié)果和數(shù)據(jù)如圖2 和表2 所示.
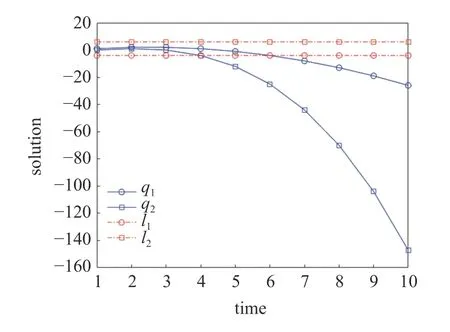
圖2 時(shí)間尺度 T =Z+ 上 q 1,q2,I1,I2 的值Fig.2 Simulations of q 1,q2,I1,I2 on the time scale T=Z+
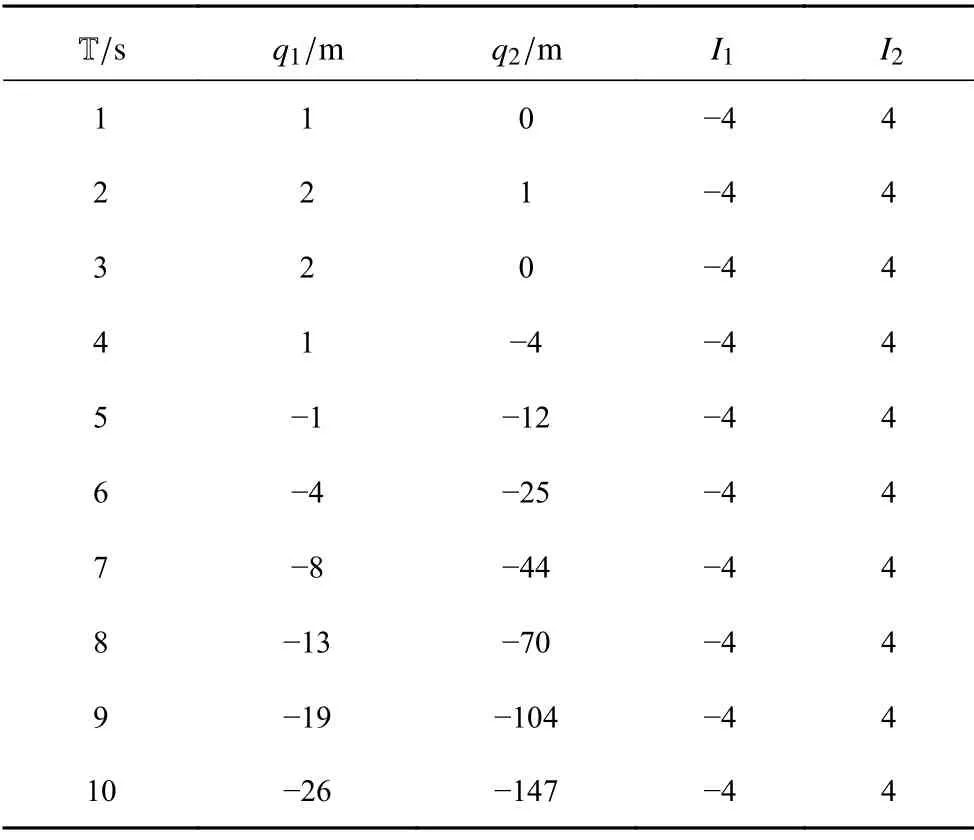
表2 時(shí)間尺度 T =Z+ 上 q 1,q2,I1,I2 的值.Table 2 The values of q 1,q2,I1,I2 on the time scale T=Z+
這里只取了t∈[1,10],實(shí)際上隨著時(shí)間的增加,仍有I1≡-4和I2≡4 .由此可知式(52) 和式(53)是守恒量,再次驗(yàn)證了定理1 的正確性.
若取 T =R ,則 σ(t)=t,μ(t)=0,Lie 對(duì)稱(chēng)性式(44)和式(45)成為
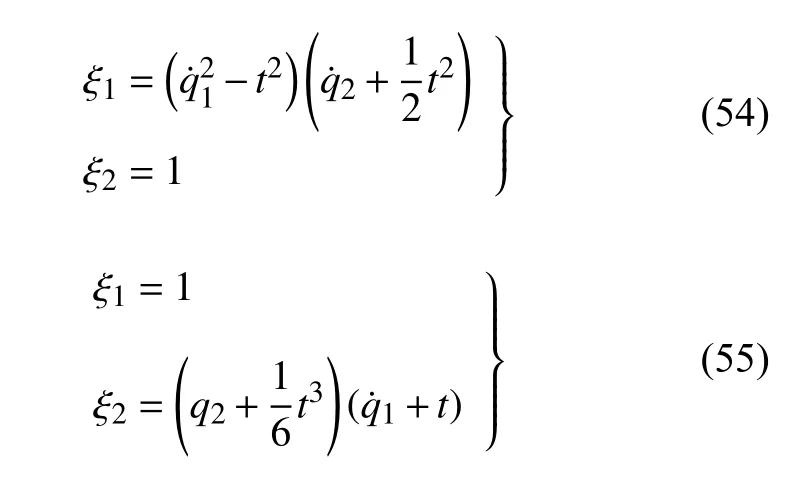
守恒量式(48)和式(49)成為

這是經(jīng)典情形的Hojman 守恒量.
7 結(jié)論
本文將Lie 對(duì)稱(chēng)性方法拓展到時(shí)間尺度上Lagrange 系統(tǒng),給出了時(shí)間尺度上Hojman 守恒量.主要貢獻(xiàn)在于:一是利用時(shí)間尺度微積分的基本性質(zhì)導(dǎo)出了時(shí)間尺度上Lagrange 系統(tǒng)導(dǎo)數(shù)運(yùn)算的兩個(gè)重要關(guān)系式.這是推導(dǎo)Hojman 守恒量的基礎(chǔ);二是由Lie 對(duì)稱(chēng)性直接推導(dǎo)得到了時(shí)間尺度上Lagrange系統(tǒng)的Hojman 類(lèi)型的守恒量.該守恒量不依賴(lài)于Lagrange 函數(shù)的結(jié)構(gòu)而僅取決于Lie 對(duì)稱(chēng)性變換的生成元.文中以時(shí)間尺度上兩自由度系統(tǒng)為例,給出了 T =,T =hZ 以及 T =R,3 種情形下的Hojman守恒量,并通過(guò)數(shù)值模擬驗(yàn)證了結(jié)果的正確性.當(dāng)時(shí)間尺度取為實(shí)數(shù)集時(shí),本文結(jié)果退化為經(jīng)典Lagrange 系統(tǒng)的Hojman 守恒量.文章的方法和結(jié)果可進(jìn)一步推廣和應(yīng)用,如時(shí)間尺度上非完整系統(tǒng),時(shí)間尺度上Birkhoff 系統(tǒng)等.

