考慮支撐面虛擬彈性剛度的多支撐點反力計算

徐金帥 齊朝暉 卓英鵬 劉海波 高凌翀

1.大連理工大學工業裝備結構分析國家重點實驗室，大連，116024 2.太原重工股份有限公司工程機械研究所，太原，030021 3.慕尼黑工業大學物流搬運與起重研究所，慕尼黑，85748

0 引言

針對各類形式支撐結構的多支撐點反力計算問題，研究人員進行了大量系統深入的研究。文獻[1-4]以力矩分配法為核心，在四支腿支撐反力計算與工程應用方面進行了研究。文獻[5-7]通過對邊界條件的假設，增加支撐點反力協調方程，解決汽車起重機支腿的超靜定求解問題。劉振國等[8]、劉永等[9]對一種八支腿高次超靜定結構的鐵路救援起重機進行支撐點反力計算。崔書文等[10]、ZHAO等[11]利用ANSYS有限元計算軟件對不同機械設備以綁定支撐點的方式進行計算。KWONHEE等[12]基于剛體模型，利用ADAMS動力學計算軟件建立支腿與支撐面之間法向接觸力模型，進行支腿支撐反力計算。姜旭等[13]采用ANSYS有限元計算軟件建立含地基模擬的非線性單元的履帶起重機底盤有限元模型，計算支重輪的支撐反力。

工程中很多機械設備并不對支撐點施加脫離支撐面的約束，即支撐面只對支撐點產生豎直向上的力，當支撐點脫離支撐面時，支撐力消失，具有單面約束效應。計算4個以上支撐點時，需要引入一定的假設與經驗判斷。采用有限元軟件進行計算時，由于其約束無法考慮單面約束效應[14]，需要通過反復計算的方式確定所需要解除約束的支撐點。采用單向受壓非線性單元模擬地基時引入的“開關效應”也造成了收斂困難，因此還需進一步完善。

實踐表明，受支撐面剛度的影響，作業過程中支撐點將產生微幅的剛體運動。本文引入與宏觀約束無關的微變量自由度來描述支撐點與支撐面間的接觸關系，同時引入虛擬彈性剛度來描述支撐面的抵抗能力，提出一種光滑化方法克服其“開關效應”。依據宏觀載荷建立了由微變量自由度表示的平衡方程，通過求解非線性平衡方程可快速求解支撐點反力。最后用數值仿真與現場試驗的對比驗證所提理論的正確性。

1 多支撐點反力計算的難點

機械設備中多支撐點的形式如圖1a所示。一旦這些支撐結構不能提供有效的支撐反力，或者超限的壓力造成支撐面的沉降，就會使設備面臨傾覆的危險，嚴重時將導致重大事故發生[15]，如圖1b所示。

(a)機械設備支撐形式

對于帶有支腿作業的機械設備尤其是起重輸送設備，底盤部分剛度大，在計算支撐點反力時，可以將其作為剛體考慮[3]，本文將所研究的支撐底盤作為剛體考慮。

建立計算模型的難點之一是如何增加未知變量數量超過平衡方程數量的協調方程。作業中的機械設備不會在支撐面上產生橫向滑移，也不會繞支撐地面法線方向轉動。對于支撐底盤，僅有豎直方向的位移以及水平面內的兩個轉動共3個自由度，可以建立3個平衡方程。而對于一般不少于4個支撐點的機械設備，每個支撐點豎直方向的反力都是一個未知變量，如何增加滿足未知變量的協調方程是一個關鍵問題；另一個難點是非光滑化支撐點反力模型的建立。支撐面對于支撐點的約束并不限制支撐點與支撐面之間出現間隙，兩者之間的間隙大于或等于零，這種單面約束只能提供單向約束反力[16]，當支撐點與支撐面接觸時，存在支撐反力；當支撐點與支撐面之間出現間隙時，支撐反力為零。這種彈性剛度不連續的“開關效應”會給方程數值求解帶來困難，因此，建立合理的支撐面虛擬彈性剛度與支撐點“縫隙”變量之間的合理關系，是另一個關鍵問題。

該方法不受支撐點數量與布置方式的限制，為復雜支撐形式的支撐點反力計算提供了一種便捷統一的求解策略。

2 支撐點的支撐形式與約束關系

很多機械設備支撐點與支撐面之間的剛體計算模型可以簡化為圖2所示的形式。

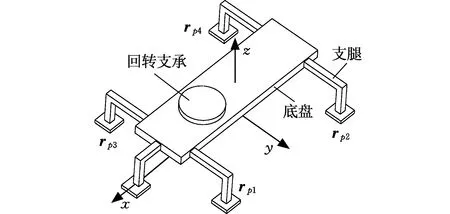
(a)支腿支撐形式

支撐點與支撐面之間的約束具有單面約束的特點，支撐面不會限制支撐點離開支撐面。對于本文計算模型，又允許支撐點使得支撐面局部產生彈性變形[17]，從而產生支撐反力，如圖3所示。

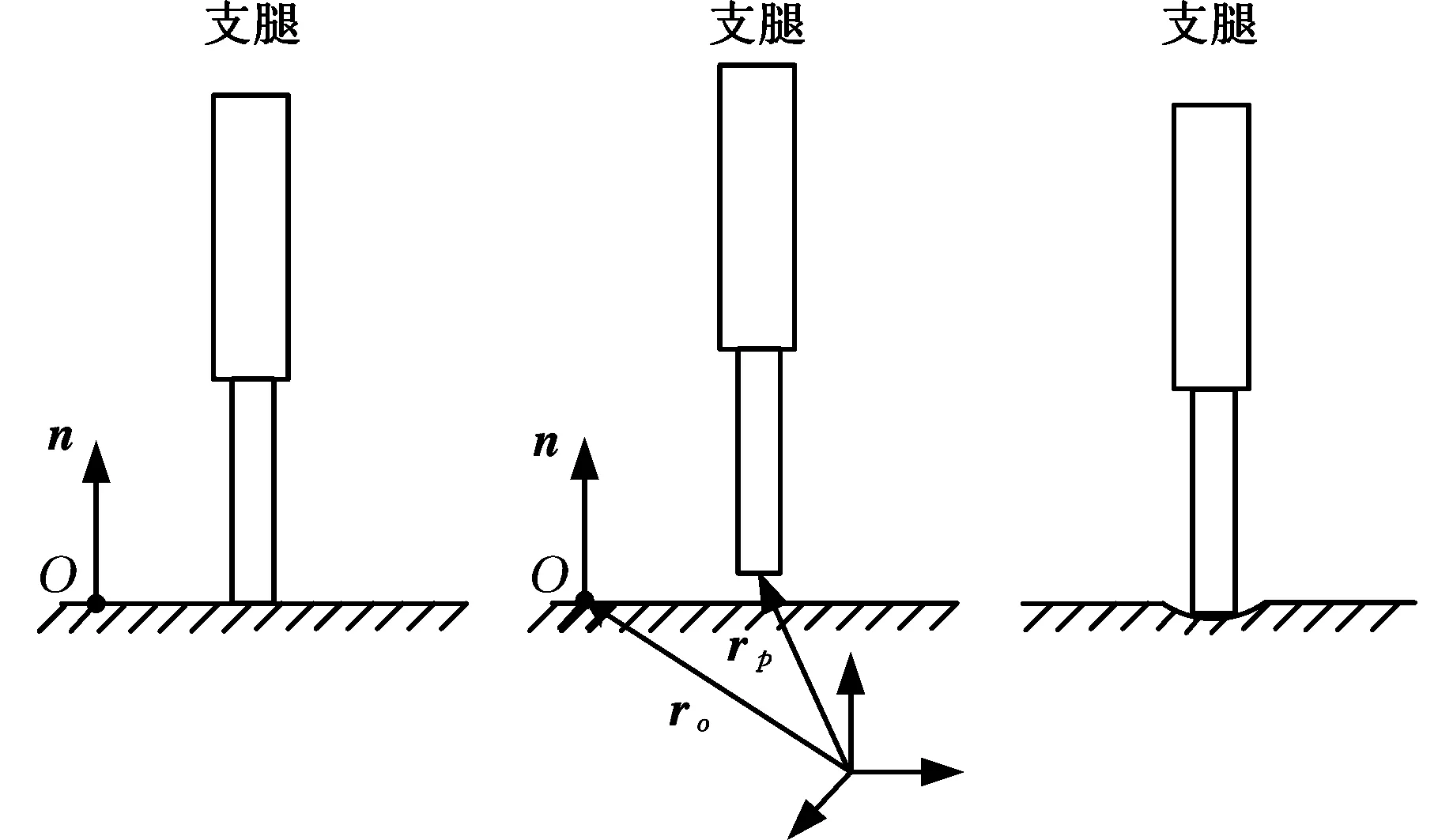
(a)支腿支撐形式

在支撐面上選取參考點o，選取n為平面的外法線矢量，如果(rp-ro)·n>0，則表示該支撐點在支撐面之上，支撐點與支撐面之間不存在支撐反力。

對于這種具有單面約束特點的模型，本文也考慮建立支撐反力與支撐點縫隙的互補方程來解決未知變量數量多于平衡方程數量的問題。假設有n個支撐點，將帶來n個縫隙未知量，通過引入的3個微變量對所有支撐點縫隙未知量進行表達，那么未知量的數量為n+3，通過建立n個支撐反力與縫隙互補方程，結合第1節中提到的3個平衡方程，可以建立滿足支撐點未知數數量的方程。這種增加方程方式的計算結果雖然能夠得到很高精度的滿足平衡方程，但存在很多計算結果明顯不符合工程實際的情況。這種情況發生的本質原因是忽略了支撐點反力與其支撐面變形量的比例關系，也從另外一個側面說明了如果僅從滿足支撐點平衡方程的原則考慮問題，可以得到多組解，這顯然是不合理的。

考慮更接近實際情況的支撐反力計算應該滿足3個原則：①支撐點滿足剛體運動；②支撐面變形越大，支撐反力越大；③支撐反力滿足力與力矩的平衡方程。因此，本文引入支撐面的虛擬彈性剛度，使支撐點的運動符合剛體運動事實。

3 模型載荷等效與支撐點接觸縫隙

3.1 模型等效載荷

對于絕大多數常規機械設備的支撐點結構布局，都采用對稱或近似對稱結構設計，故對于簡化的計算模型，可以根據支撐點位置參數確定其平面形心點，圖2中坐標系原點的所在位置為所有支撐點的平面形心。外部載荷均可轉換為垂直載荷與傾翻力矩兩種載荷形式，通過回轉支承將載荷傳遞到支撐點，然而并不是所有的回轉支承所在的位置都是支撐點平面形心位置，因此，需要將載荷作用位置等效平移至平面形心處，稱之為力系等效。力系等效反映了作用在剛體上載荷的一個非常重要的性質[18]。從本質上來說，力系等效本質上是力的虛功率等效的一種體現。

如圖4所示，rp、ro為剛體在總體坐標系中的矢徑，rpo為p點到o點的矢徑。對于剛體上任意一點，其相對于總體坐標系的角速度ω是相同的。剛體上p點所承受的合力與力矩分別為Fp、Mp，將p點載荷等效到任意點o處的力系為Fo、Mo，o點在總體坐標系中的矢徑和速度分別為

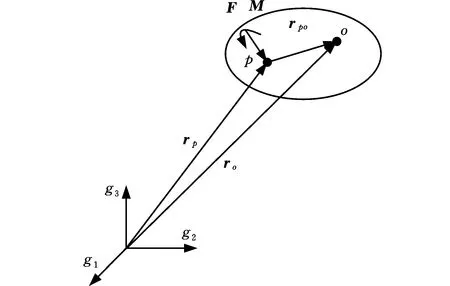
圖4 剛體的力系等效圖Fig.4 Force system equivalence on rigid body

ro=rp+rpo

(1)

(2)

p點的虛速度

(3)

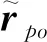
(4)

根據虛功率原理，若剛體上兩點的力系作用效果相同，則它們對應的虛功率是等價的，即

(5)

將式(3)代入式(5)，可以得到

(6)

由式(6)可以得到

(7)

對于一個剛體來說，力的作用效果反映在力系虛功率上，如果兩個力系虛功率一致，那么這兩個力系作用效果相同。

3.2 微變量與接觸縫隙的關系

對于工作狀態中的機械設備，引入的3個微變量分別為豎直方向的微小位移、支撐面內繞兩個軸矢量方向的微小轉角。引入的微變量僅在計算接觸點的支撐反力過程中出現，它不會改變整體模型的宏觀約束。

本文中所描述的縫隙包含兩個方面的意義，當計算的縫隙數值為正值時，支撐點與支撐面之間出現間隙；當計算的縫隙數值為負值時，支撐點使得支撐面產生變形量。所有支撐點的接觸間隙都可以通過這3個微變量進行表達。每個支撐點的縫隙gi為支撐點軸向位移以及由小轉角產生的剛體轉動疊加得到：

(8)

式中，gi(i=1,2,…,n)為任意支撐點縫隙；[uαβ]T為支撐點的3個微變量自由度；[rixriy0]T為任意支撐點矢徑。

4 支撐面虛擬彈性剛度與支撐點載荷

4.1 虛擬彈性剛度曲線光滑化與支撐點載荷

工程中的機械設備作業環境相對復雜多變，支撐面具有一定彈性，要準確得到其作業的支撐面彈性剛度是比較困難的[5]，對于本文的計算方法沒有具體實際意義。本文計算模型所采用的支撐面剛度為一虛擬彈性剛度數值，并不是將其作為實際彈性剛度，其數據僅在計算中作為過程變量使用。支撐點作用在支撐面上，支撐面所產生的變形越大，支撐載荷越大。假設支撐面虛擬彈性剛度為K，其單位量綱與計算中所采用的載荷以及位置單位量綱保持一致。其中，任意支撐點反力Fi與縫隙gi的關系滿足以下方程：

(9)

通過式(9)可以將縫隙gi與彈性剛度K之間的關系用圖5a來形象地表示。這種分段函數關系使非線性數值計算產生困難，而借鑒研究人員對非光滑化庫侖摩擦模型的處理方式[19-20]，采用非線性函數對縫隙-虛擬彈性剛度模型進行修正，使其成為光滑化函數，能夠很好地解決數值求解的困難，如圖5b所示。

(a)分段函數 (b)光滑化函數圖5 縫隙-虛擬彈性剛度函數關系Fig.5 Relationship between gap-virtual elastic stiffness

在實際問題中，對構造的插值多項式的要求不僅僅局限于插值點的函數值相同，還需要滿足若干階導數值相同。在縫隙gi負值段取縫隙參數的微段h作為過渡段。采用五次赫米特插值，使彈性剛度值能夠均勻過渡，同時保證了整個過渡曲線的二階連續性。K(x)為所取微段內任意點所對應的虛擬剛度值：

K(x)=N1K(x1)+N2K(x2)+N3K′(x1)+
N4K′(x2)+N5K″(x1)+N6K″(x2)

(10)

其中，x1=0，x2=-h，型函數Ni(i=1,2,…,n)為

Ni=aix5+bix4+cix3+dix2+eix+fi

(11)

根據虛擬彈性剛度與支撐點縫隙的關系，過渡函數初值以及一二階導數值確定如下：

(12)

結合式(10)～式(12)，得到虛擬彈性剛度過渡函數：

K(d)=d3(10-15d+6d2)K

(13)

d=-gi/h

結合式(9)、式(13)，式(9)改寫為

(14)

4.2 支撐反力的非線性平衡方程與初值

根據計算模型的外部載荷對，對所有支撐點可以建立以下3個平衡方程：

(15)

式中，Fz、Mx、My為計算支撐反力計算工況下，機械設備對應的外部垂直載荷與傾翻力矩；Fi為第i個支撐點的支撐反力。

對于非線性方程的求解，合理的初值能夠更好地提高計算效率以及計算結果的準確性。多支撐點機械設備的初始狀態是無外部載荷，僅考慮整機自重。整機自重使得機械設備的支撐點在彈性支撐面上有豎直向下的位移，而整機的剛體轉動在初始狀態下可以忽略，因此，對于具有n個支撐點的計算模型，本文所引入的3個微變量的初值可以按照以下方式表達：

(16)

4.3 虛擬彈性剛度與微長度段縫隙段參數

作為計算中的過程變量，支撐面的虛擬彈性剛度K雖然不代表支撐面的實際剛度，但其剛度值與微長度段縫隙參數h的匹配對最終的計算結果是有影響的。一個重要原則是非線性方程組的最終數值解對應的虛擬彈性剛度值，取值必須在光滑過渡曲線段之外，使所有支撐點反力大小與支撐面的彈性變形遵守統一的比例原則。顯然對于微長度段h的取值在虛擬彈性剛度值確定的情況下越小，越容易使虛擬彈性剛度值在過渡曲線段之外。但如果取值過小，會使過渡段光滑化曲線變化率隨之增加。在符合微變量概念前提下，虛擬彈性剛度可以取較大值，在微長度段h取值與虛擬彈性剛度的乘積不大于0.1的條件下，會得到穩定的計算結果。

5 數值計算

5.1 數值算例對比

對于常規四支腿形式的汽車起重機支腿反力計算，有多種計算方法，但到底哪一種更為合理準確，至今未有定論[21]。國內外很多起重機廠家也給出了工程中計算算法，結合文獻[22]給出的4種不同算法在QY16型汽車起重機參數下的計算結果對比。QY16型汽車起重機的支腿與載荷參數見表1，兩種不同臂架回轉角度θ下的計算結果對比見表2、表3，其中，RA、RB、RC、RD分別對應圖6中4個支撐點的反力。

表1 QY16汽車起重機參數Tab.1 Parameters of QY16 truck crane

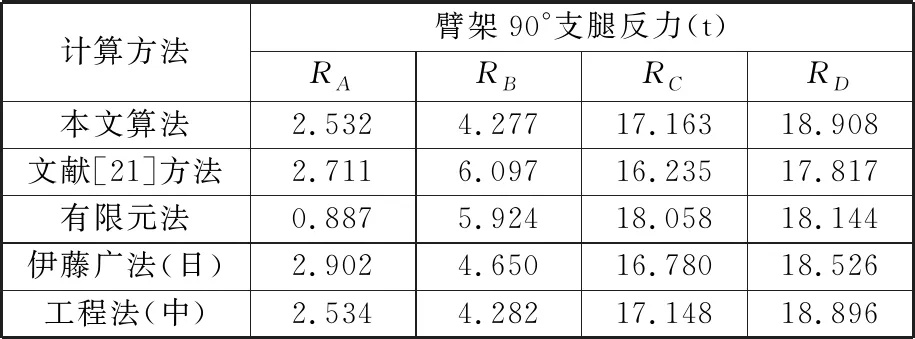
表2 90°臂架角度計算數據Tab.2 Calculation data with 90° boom angle

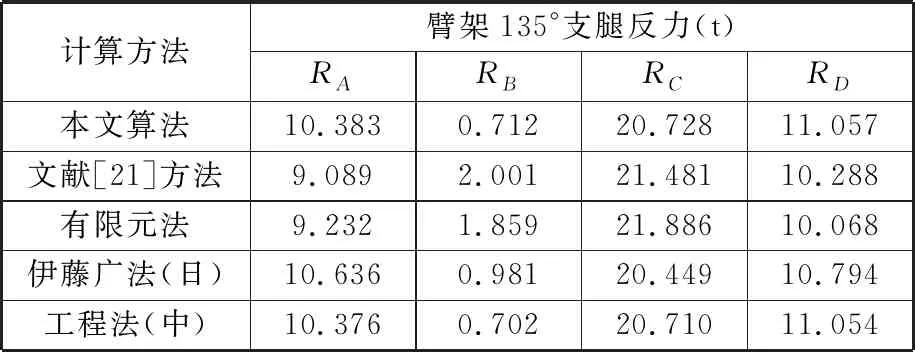
表3 135°臂架角度計算數據Tab.3 Calculation data with 135° boom angle

圖6 四支腿汽車起重機計算模型簡圖Fig.6 Calculation model of truck crane with four outriggers

由表3數據對比可知：采用不同的假設條件得到的計算數據有一定差異，但基本趨勢保持一致，最大支腿力差比為5%。本文滿足以下兩個基本事實：①支撐點滿足剛體運動；②支撐反力大小與支撐面彈性變形成線性比例。伊藤廣法與工程法同樣基于剛體假設計算，在簡單四點對稱形式下計算數據一致性較高。文獻[21]和有限元法考慮底盤的柔性，前者支撐點與支撐面綁定，忽略支撐點剛體運動事實；后者則直接將支撐部件進行簡化，用梁單元來逼近結構柔性。由計算數據可以看出，結構柔性對于支腿反力有一定的影響。結合本文解決多點支撐反力的思想，將結構柔性考慮在內也值得深入研究。

5.2 產品試驗數據對比

以太原重工股份有限公司TZT1200型履帶底盤伸縮臂架起重機為試驗機型，通過測試支腿油缸的壓力數據，將壓力與支腿力進行換算，對比試驗與計算數據，如圖7所示。計算與試驗對比工況參數見表4，計算結果與試驗結果對比數據見表5。

表4 TZT1200參數Tab.4 Parameters of TZT1200

圖7 TZT1200吊載試驗Fig.7 TZT1200 lifting test

本產品底盤剛度相對較大，而外伸支腿結構柔性對支撐點反向載荷有一定影響。由表5計算數據比較可以發現，基于本文方法進行計算，支腿最大載荷點誤差2%左右，可以滿足工程精度要求。本文算法數據與有限元法計算最大誤差在5%以內，同時在四支腿均受力的情況下，本文算法與工程法結果是一致的，驗證了計算方法的可靠性。

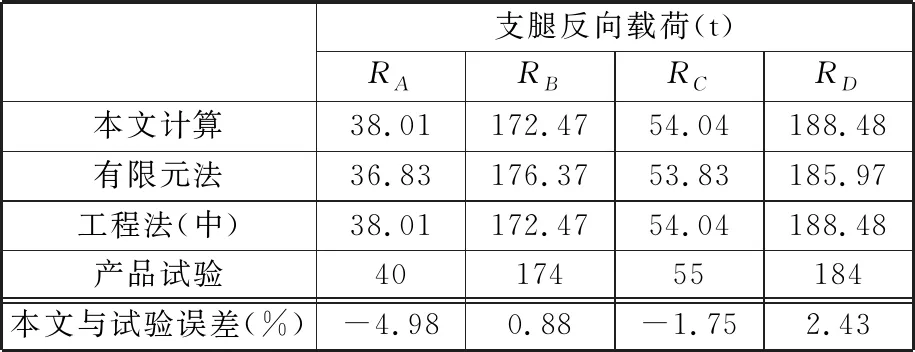
表5 TZT1200計算結果與試驗結果對比Tab.5 Comparisons between calculation results and test results of TZT1200

5.3 履帶底盤與環形軌道多點支撐算例計算

以650 t級履帶起重機為例，計算高次超靜定形式支撐點反向載荷，選取4種計算工況，不同臂架工作角度下的輸入參數見表6，計算結果如圖8所示。

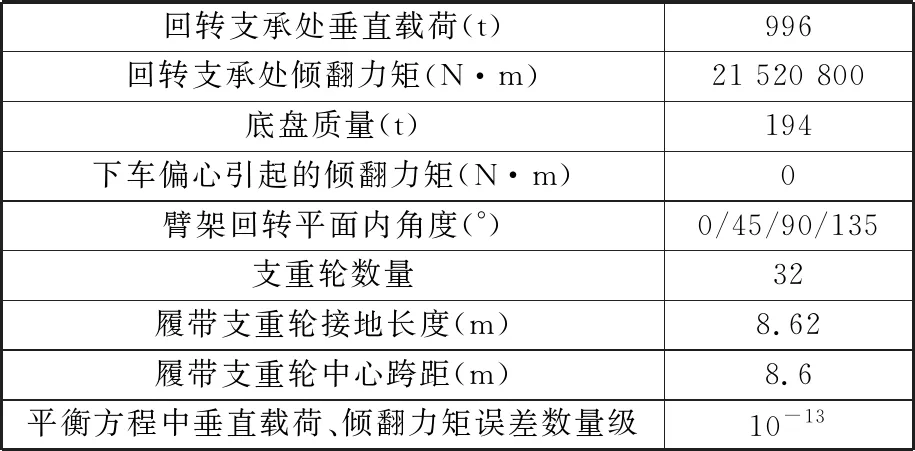
表6 履帶起重機計算參數Tab.6 Calculation parameters of crawler crane

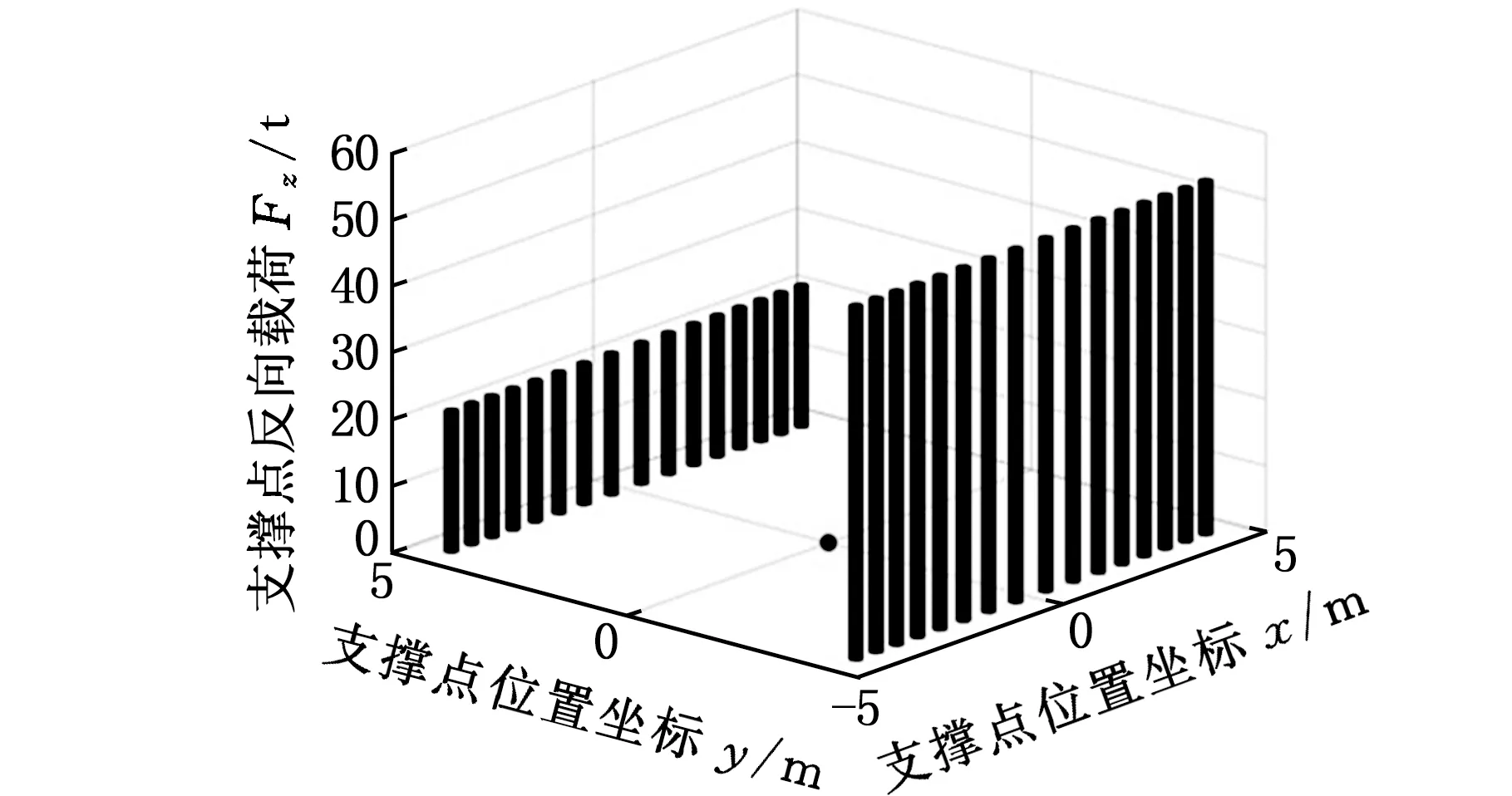
(a)0°角工況

基于ANSYS有限元計算軟件建立底盤結構板殼單元有限元模型，在考慮彈性地基的基礎上，計算表6中支重輪載荷較復雜的45°與90°角工況，計算結果與本文結果對比曲線如圖9所示。可以看出，對于具有剛度較大的履帶起重機底盤，在承載狀態下，其支重輪載荷與本文計算結果趨勢一致，支重輪載荷誤差在0.5%以內。

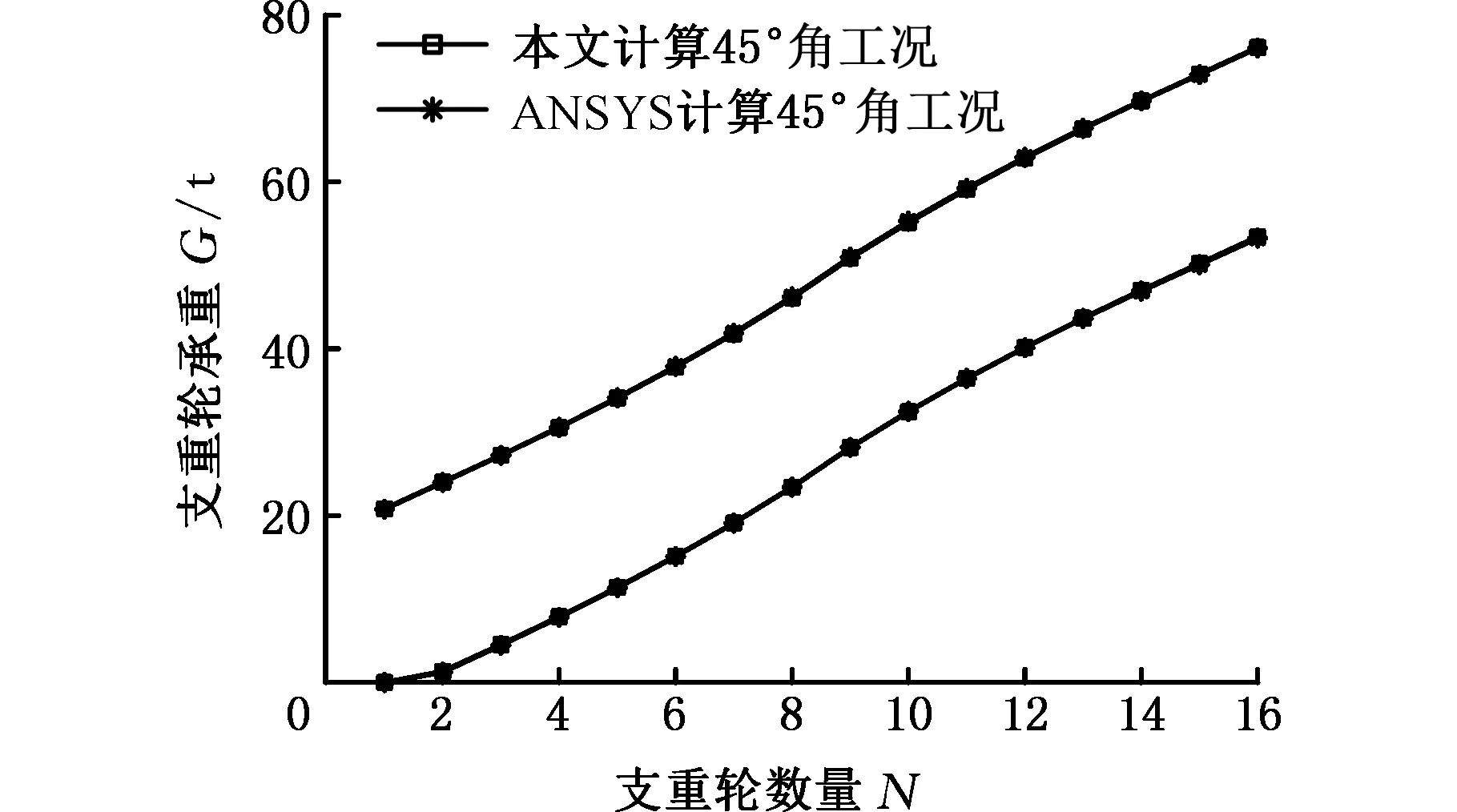
(a)45°角工況對比曲線

以320 t級船用起重機為例，選取固定臂架角度，不同吊重下的兩種工況，相關計算輸入參數見表7，計算結果如圖10所示，可以看出存在滾輪脫離支撐面的情況。

表7 船用起重機計算參數Tab.7 Calculation parameters of marine crane

基于ANSYS有限元計算軟件，根據320 t船用起重機滾輪支撐方式，建立滾輪安裝結構有限元模型，滾輪支撐軌道可作為剛體支撐件考慮，將表7中兩種不同承載工況下的滾輪載荷進行計算，計算結果與本文結果對比曲線如圖11所示，對于底盤剛度大的船用起重機滾輪載荷趨勢一致，載荷最大誤差在1%以內。

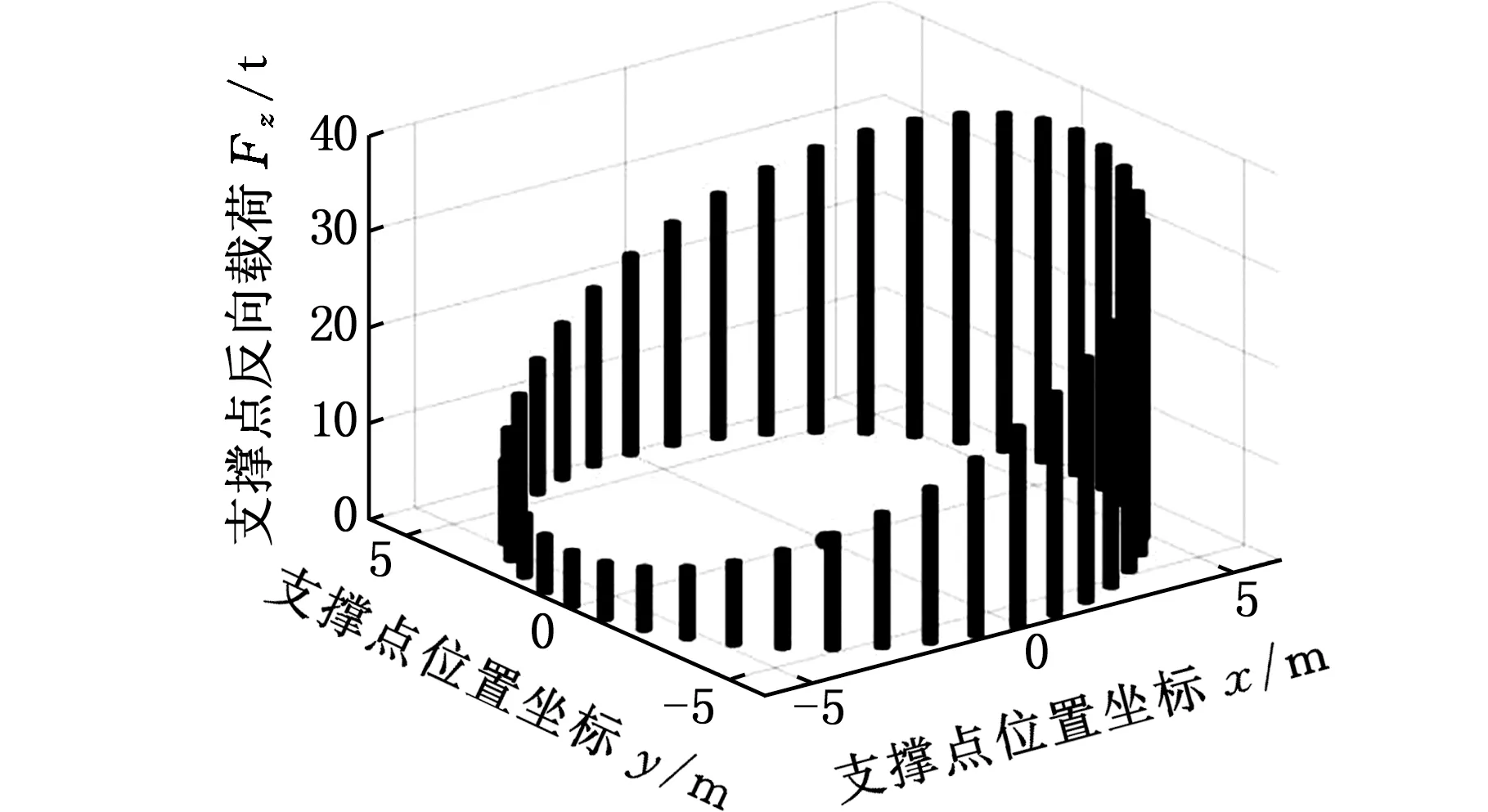
(a)830 t垂直載荷工況

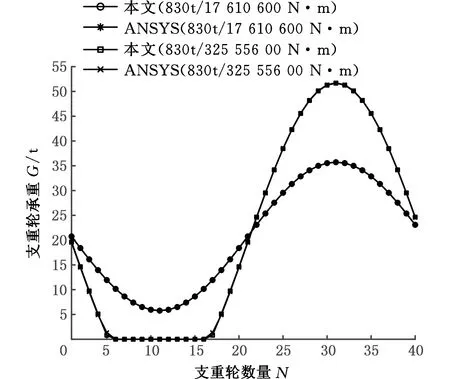
圖11 支撐點反向載荷計算結果數據對比Fig.11 Comparison of calculation results of backload of support point

通過兩種不同布置形式的多支撐點反向載荷計算與數值算例對比曲線可以看出，本文計算方法能夠針對多支撐點在滿足剛體運動的前提下，不受支撐點布置方式、支撐點數量因素的限制，不僅可以快速計算各支撐點反向載荷，而且能夠高精度地滿足平衡方程。

6 結論

(1)本文方法避免了采用非線性單元計算支撐反向載荷耗時長問題，能夠方便地計算具有單面約束特征的高次超靜定多支撐點反向載荷。

(2) 借鑒非光滑化庫侖模型的處理方法，將具有單面約束特點的支撐點與支撐面之間的虛擬彈性剛度進行光滑化處理，這種方式能夠解決類似形式非線性方程數值求解的困難。

(3) 通過算例數值計算及工程試驗對比，驗證了所提計算方法的有效性。該方法可成為工程中計算具有高次超靜定多支撐點支撐反向載荷的新途徑。

(4)在支撐結構具有一定柔性的情況下，采用剛體假設計算也會帶來一定的誤差。因此，在考慮支撐面真實的剛度系數、支撐部件的彈性變形的基礎上，基于支撐點的單面約束特點，綜合考慮多變量之間的耦合影響，研究多支撐點反向載荷計算是本文后續研究的內容。