基于深度學習與子域適配的齒輪故障診斷

揭震國 王細洋 龔廷愷

1.南昌航空大學飛行器工程學院，南昌，330063 2.南昌航空大學通航學院，南昌，330063

0 引言

齒輪及齒輪箱是金屬切削機床、直升機動力傳動系統等設備中常用的傳動部件，據統計，這些設備80%的機械故障由齒輪引起[1]，因此，齒輪故障診斷對降低設備維修費用和防止突發性事故具有重要意義。

近年來，深度學習成為機械智能故障診斷的一種主流趨勢[2]，其中，卷積神經網絡(convolutional neural network, CNN)是一種代表性方法。CNN是圖片和視頻識別領域應用最為廣泛的方法，已被廣泛應用到故障診斷領域。ZHANG等[3]將一種基于自適應批歸一化的第一層寬卷積核深度卷積神經網絡模型用于故障診斷。吳春志等[4]針對傳統故障診斷方法難以解決端對端故障識別的問題，提出了一維卷積神經網絡的故障診斷方法。胡蔦慶等[5]針對行星齒輪箱需要專家知識才能實現故障識別的問題，提出了一種經驗模態分解和CNN相結合的智能故障診斷方法。但CNN的診斷效果受限于兩個條件：一是CNN需要大量的已標注訓練集才能達到令人滿意的識別率；二是CNN要求訓練集和測試集具有相同的分布。然而，在生產實際中難以滿足以上兩個條件，這會影響CNN的泛化能力，甚至使模型不再適用[6]。

近年來，深度遷移學習成為解決以上問題的一種主流方法，其模型的研究取得了很大進展[7-10]，并被應用到故障診斷領域。LI等[11]為了解決軸承數據域差異的問題，提出了一種多層域適配模型。YANG等[12]提出了一種將實驗室軸承數據遷移到機車軸承數據的故障診斷方法，該方法采用多層域適配和偽標記學習。HAN等[13]提出了一種基于聯合分布適配的深度遷移學習框架，通過將邊緣分布適配擴展到聯合分布適配來提高分布適配的準確度。

以上深度遷移學習方法雖然在故障識別方面取得了一定的效果，但存在以下兩個問題：一是用于特征提取的CNN模型性能較差，影響了遷移效果；二是僅考慮全域的分布差異，而沒有考慮相關子域的分布差異。針對以上問題，本文提出了基于深度學習與子域適配的齒輪故障診斷方法：首先構建一維卷積神經網絡，從源域數據和目標域數據中提取可遷移特征；然后采用多核-局部最大均值差異來測量可遷移特征相關子域的分布差異，并將測得來的分布差異作為反向傳播的優化目標；最后使用訓練完成的模型識別無標簽目標域的健康狀況。

1 卷積神經網絡、最大均值差異及域適配

1.1 卷積神經網絡

CNN最大的優勢是可以直接從數據中自動學習特征，無需人工提取即可實現高效的識別。CNN的單元結構主要包括卷積層、池化層和全連接層。

卷積層是CNN的核心，它的主要作用是提取輸入的不同特征，低層卷積層提取低級的特征，高層卷積層提取更深層的特征。卷積層的計算公式如下：

X(l)=X(l-1)*K(l)+B(l)l=1,2,…,L

(1)

式中，X(l-1)、X(l)、K(l)、B(l)分別為第l個卷積層的輸入矩陣、輸出矩陣、權重矩陣、偏置矩陣；符號“*”表示卷積運算符；L為CNN的卷積層數。

池化層又稱下采樣，主要作用是通過減少網絡的參數來減小計算量，并在一定程度上控制過擬合。最大池化是最常用的池化方法，其計算公式如下：

V(l)=max(A(l)(St+1),A(l)(St+2),…,
A(l)(St+W))

(2)

t=0,1,…,M(l)-1

式中，V(l)為第l個池化層的輸出矩陣；A(l)為X(l)的激活向量；S、W分別為池化核的步長、大小，一般S=W；M(l)為第l個池化層的平均段數。

全連接層是一個常規的網絡結構，它的作用是全連接經過多次卷積和池化所得的高級特征，輸出對結果的預測值。全連接層的計算公式如下：

XF=Z*KF+BF

(3)

式中，XF、KF、BF分別為全連接層F1的輸出矩陣、權重矩陣、偏置矩陣；Z為第L個池化層的展開向量。

一般采用Softmax回歸進行結果預測，Softmax回歸的計算公式如下：

(4)

式中，θ為模型的待訓練參數；C為數據的故障類別數；p為樣本xi屬于類別c的概率值；Pi為樣本xi的概率分布向量。

1.2 最大均值差異

作為一種衡量分布差異的非參數距離指標，最大均值差異(maximum mean discrepancy, MMD)被廣泛應用于測量源域和目標域的分布差異。MMD的計算流程[14]如下：在同一個映射函數下將源域和目標域映射到一個再生核希爾伯特空間(reproducing kernel Hilbert space, RKHS)，然后計算兩域的分布差異。MMD的線性無偏估計表示為

(5)

式中，H表示RKHS；Ds、Dt分別為源域、目標域；p、q分別為源域、目標域的分布；ns、nt分別為源域、目標域的樣本數；xs、xt分別為源域、目標域中的樣例；k(·)為核函數。

1.3 域適配

近年來遷移學習被廣泛應用到各個領域，遷移學習的定義如下[6]：給定一個源域Ds和學習任務Ts，一個目標域Dt和學習任務Tt，使用Ds和Ts中的知識提升Dt中目標預測函數f(·)的學習，其中，Ds≠Dt或Ts≠Tt。

在訓練數據和測試數據之間的分布存在差異的情況下，學習一個有判別力的模型稱為域適配。LONG等[8]提出了深度適配網絡(deep adaptation network, DAN)，將深度卷積神經網絡應用到域適配場景。DAN實現了網絡AlexNet[15]的多層適配和基于多核-最大均值差異的適配層。DAN的優化目標由以下兩部分組成：源域和目標域的損失函數，源域和目標域的分布距離。優化目標可表示為

(6)

式中，a為源域和目標域有標簽的樣本；J(·)為損失函數；λ為平衡系數，λ>0。

2 基于深度學習與子域適配的齒輪故障診斷

針對標注故障數據不足的問題，本文提出了深度學習與子域適配的齒輪故障診斷方法。本方法由特征提取、子域適配和模式識別三部分組成：①特征提取由一維卷積神經網絡從源域數據和目標域數據中提取可遷移特征；②子域適配首先使用多核-局部最大均值差異測量可遷移特征相關子域的分布差異，然后將測得的分布差異作為目標函數的一部分訓練優化；③模式識別利用訓練完成的模型識別目標域的健康狀況。所提方法流程圖見圖1。

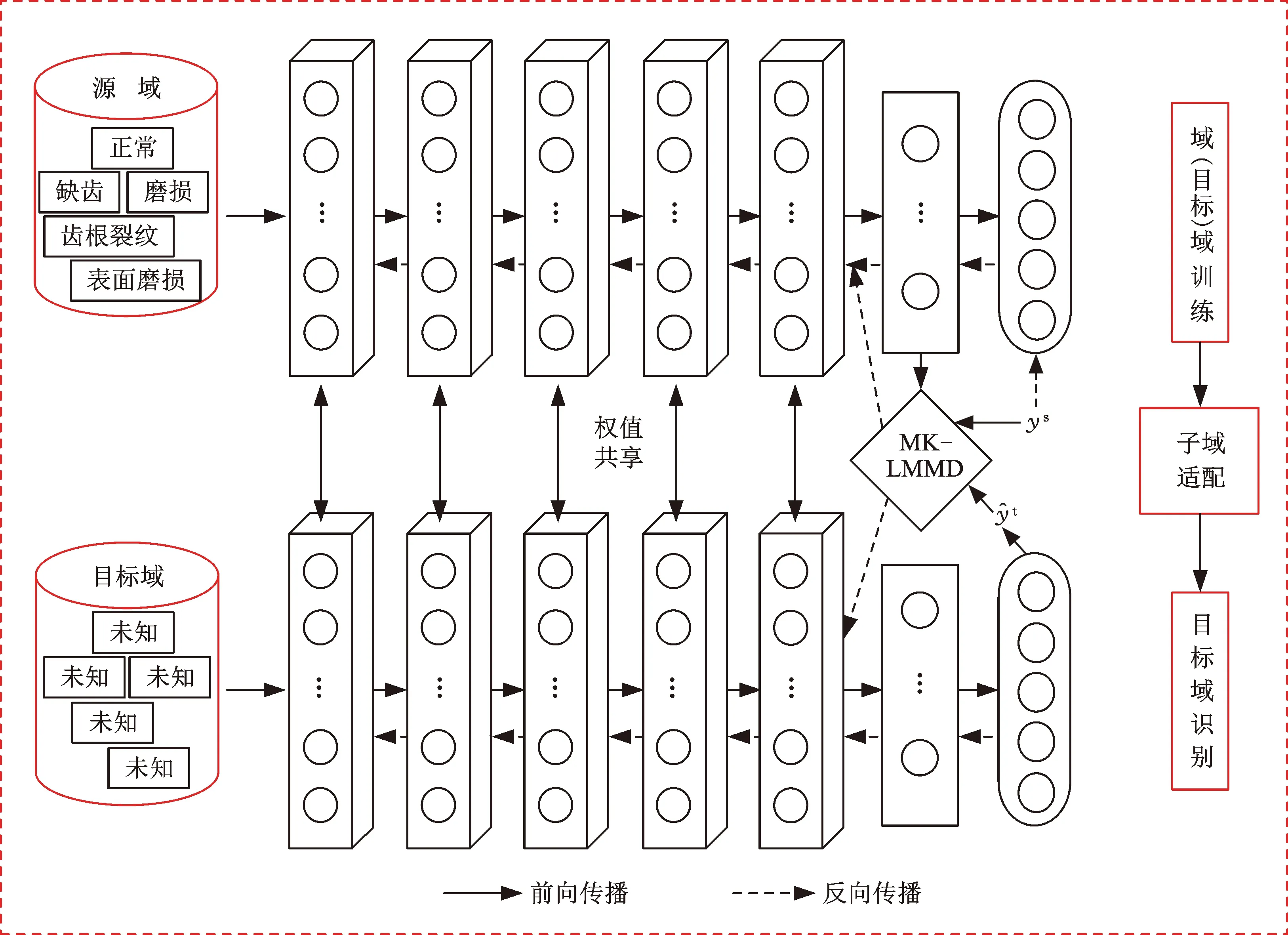
圖1 基于深度學習與子域適配的齒輪故障診斷方法流程圖Fig.1 Flow chart of gear fault diagnosis based on deep learning and subdomain adaptation

2.1 一維卷積神經網絡

針對一些深度遷移學習方法用于特征提取的CNN模型性能較差的問題，本文提出了一維卷積神經網絡(one dimensional convolutional neural network, 1D-CNN)，1D-CNN在AlexNet的基礎上進行了改進，具體改進如下：

(1)采用一維卷積核和第一層寬卷積核。一維卷積核可以直接從一維的振動信號中提取特征，第一層寬卷積核可以提取輸入信號的短時特征。

(2)去除局部響應歸一化層和第二個全連接層。局部響應歸一化層提升網絡性能并不明顯，可采用Dropout層代替，它可以有效提升網絡的識別性能和抑制過擬合。第二個全連接層在齒輪故障診斷中對識別率影響不大，但會增加大量的訓練參數。

一維卷積神經網絡的結構共有7層，包含5個卷積層、2個全連接層，結構見表1，其中，Dropout層的棄置率為50%。

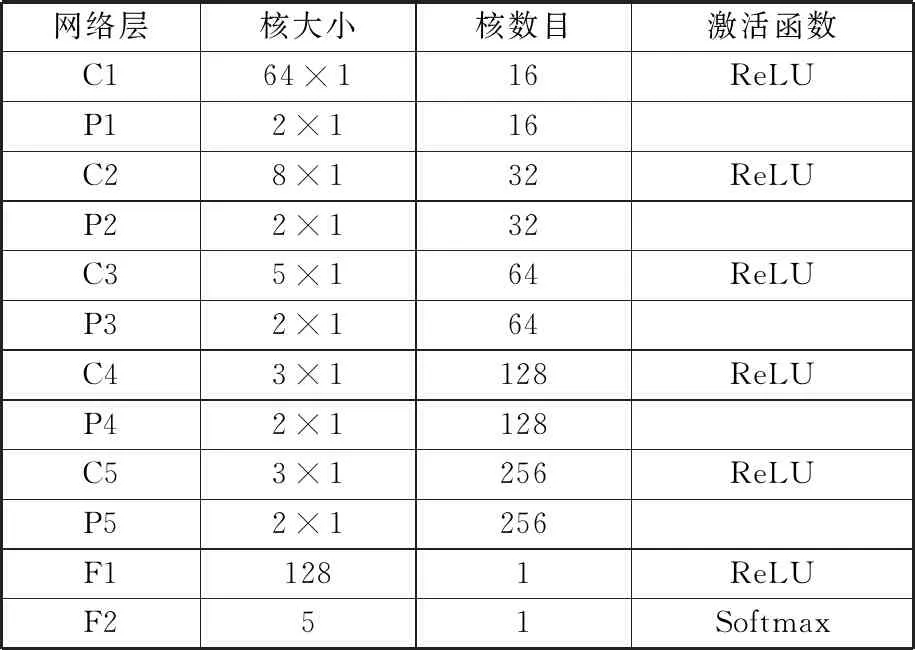
表1 1D-CNN結構Tab.1 Structure of 1D-CNN

2.2 多核-局部最大均值差異

源域與目標域的數據來源于不同的工況導致1D-CNN提取出的可遷移特征有較大的分布差異。為此，采用多核-局部最大均值差異(multi-kernel local maximum mean discrepancy, MK-LMMD)來測量可遷移特征相關子域的分布差異，MK-LMMD可定義為

(7)

式中，p(c)、q(c)分別為源域、目標域中類別c的分布；E(·)為數學期望；f(·)為映射函數(即高斯核函數)。

假設每個樣本屬于類別c的權重為w(c)，那么樣本xi的權重可定義為

(8)

式中，yic為獨熱向量yi的第c項。

基于高斯核函數將源域與目標域的可遷移故障特征從原空間嵌入RKHS，MK-LMMD的線性無偏估計可表示為

(9)

式中，Asf、Atf分別為源域、目標域第f層的激活向量。

MK-LMMD的效果取決于核函數的選擇，核函數選擇不當將影響其在域適配中的應用，為此引入最優多核選擇方法[16]。多核高斯核函數凸組合為

(10)

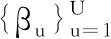
2.3 子域適配

子域適配將MK-LMMD測得的分布差異作為目標函數的一部分進行訓練，以最小化子域的分布差異。不同于域適配，子域適配不僅能對齊源域與目標域的全局分布，還能對齊相關子域的分布。域適配與子域適配的效果示例圖見圖2。本文根據類標簽將一個領域下同一類別的樣本劃分到一個子域中。

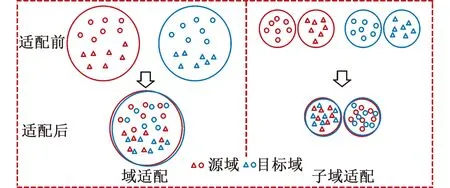
圖2 域適配與子域適配的效果示例圖Fig.2 Effect sample diagram of domain adaptation and subdomain adaptation

由圖2可知，域適配后，源域與目標域的全局分布幾乎一致，但兩子域分布的間距很小，這將導致分類錯誤。子域適配后，源域與目標域的全局分布和子域分布幾乎都達到了一致。綜上，子域適配可以有效地提高分類精度。

最小化式(9)可實現兩個領域間的全局分布和子域分布的同時適配，即子域適配的優化目標為

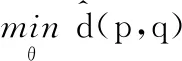
(11)

(12)

式中，τ-2為估計方差。

綜上，子域適配的優化目標可表示為

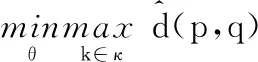
(13)

2.4 模型的訓練

(14)

結合式(6)、式(13)、式(14)構建以下目標函數：

(15)

式中，α為偽標簽的懲罰系數。

由式(15)可知，模型的優化目標由三部分組成：源域的損失函數、目標域的損失函數及源域與目標域相關子域的分布距離。目標函數的具體訓練過程如下：

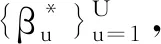
(3)反向傳播。①優化算法選用ADAM，反向更新待訓練參數集θ；②執行步驟(2)。

3 實驗驗證

3.1 數據集描述

齒輪正常和故障狀態下的振動信號采集于美國SQI公司的DPS故障預測綜合實驗臺，其結構由電機、行星齒輪箱、平行齒輪箱和負載齒輪箱等組成，如圖3所示。實驗在平行齒輪箱上進行，平行齒輪箱齒輪為漸開線直齒圓柱齒輪，齒輪箱結構簡圖見圖4，圖中N1～N4分別表示輸入軸齒輪、中間軸大齒輪、中間軸小齒輪、輸出軸齒輪的齒數。在中間軸小齒輪上人工植入磨損、表面磨損、缺齒、齒根裂紋故障，如圖5所示。

圖3 實驗臺Fig.3 Test rig

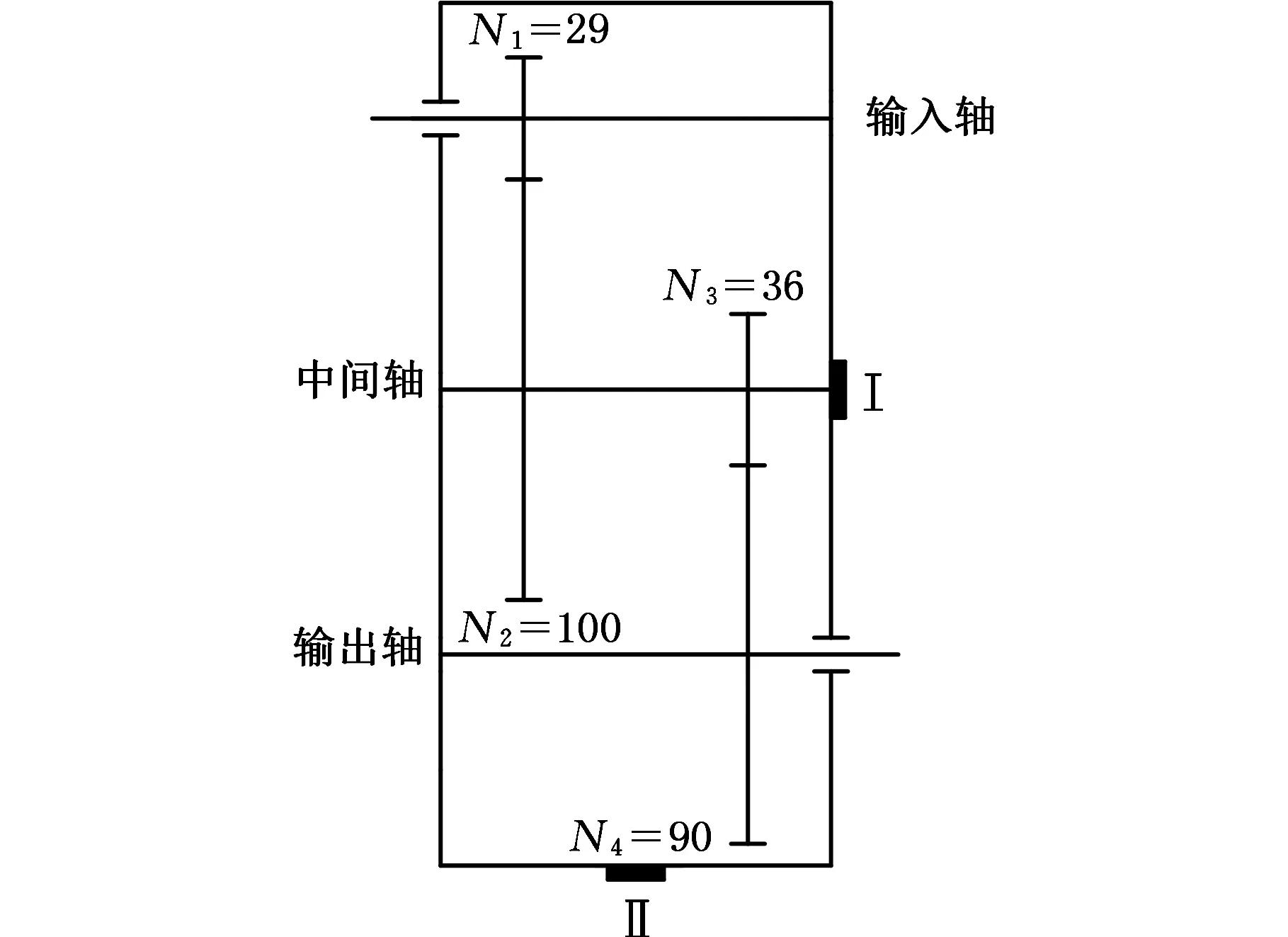
圖4 平行齒輪箱結構簡圖Fig.4 Structure diagram of parallel gearbox

(a)正常 (b)缺齒 (c)表面磨損

采用三軸加速度傳感器采集齒輪振動信號，采樣頻率為20.480 kHz，在電機轉速1800 r/min和4種不同負載(0、0.45 N·m、1.35 N·m與0～1.8 N·m變負載)工況下采集齒輪振動信號。以1024個采樣點截取樣本，得到數據集A、B、C和變工況下的數據集D，按照4∶1的比例將數據集分成訓練集與測試集，各數據集的詳細信息見表2。為模擬生產實際中帶標簽故障數據不足的狀況，在模型的訓練過程中，數據集B、C、D的樣本無標簽。

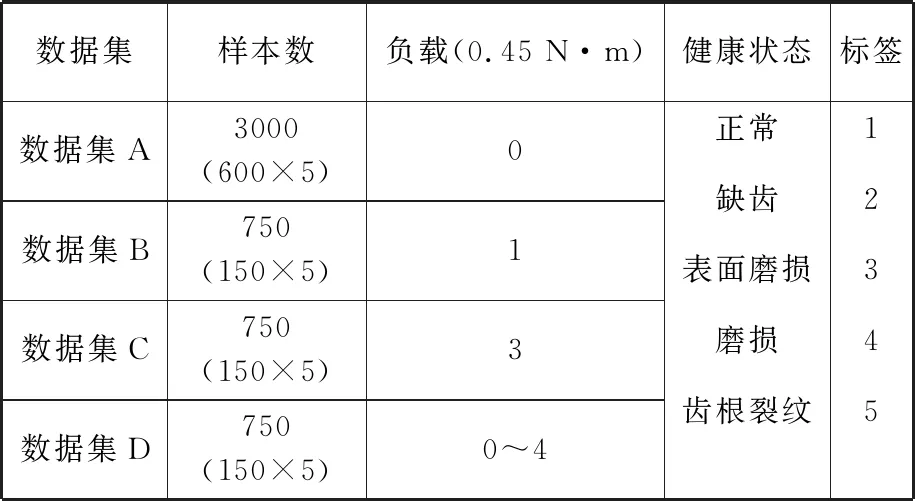
表2 數據集的詳細信息Tab.2 Details of the datasets

3.2 對比實驗

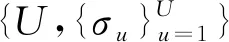
(16)

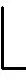
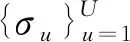
(17)

(18)

式中，e為訓練次數；αf=1[18]；γ=10[19]；αe為隨訓練次數變化的懲罰系數α；λe為隨訓練次數變化的平衡系數λ。

對比實驗以類標簽為子域劃分依據，同一類別的樣本劃分到一個子域中。為了保證實驗結果的穩定性，每種算法重復10次實驗。

在1D-CNN的結構參數優化過程中發現，第一個卷積層的卷積核大小和全連接層單元數對故障的診斷結果影響較大，結果見表3與表4。

表3 卷積核大小對診斷結果的影響Tab.3 Effect of kernel size to diagnosis result

表4 全連接層單元數對診斷結果的影響Tab.4 Effect of fully connected layer neural number to diagnosis result

由表3可知，第一個卷積層選用較大的卷積核可以有效提高診斷精度，但當卷積核大于64×1時，診斷精度逐步降低。由表4可知，全連接層單元數增大可以有效提高診斷精度，但當單元數大于128時，診斷精度逐步降低。

為研究多核核函數集系數、懲罰系數和平衡系數對診斷結果的影響，分別以這些參數為變量進行對比實驗。其中，核函數數量-步長(u-ζ)從{[5-2], [7-2], [3-2], [5-22], [5-20.5]}中取值，懲罰系數α從{αe, 0.01, 0.1, 0.5, 1}中取值，平衡系數λ從{λe, 0.01, 0.05, 0.1, 0.2}中取值。以下實驗為所提方法在遷移任務A→B上的診斷結果，各參數不同時為變量，如以核函數數量-步長為變量(常量下為5-2)時，懲罰系數和平衡系數為“常量”αe和λe，結果見表5～表7。

表5 核函數數量和步長對診斷結果的影響Tab.5 Effect of kernel number and step-size to diagnosis result

表6 懲罰系數對診斷結果的影響Tab.6 Effect of penalty parameter to diagnosis result

表7 平衡系數對診斷結果的影響Tab.7 Effect of tradeoff parameter to diagnosis result

由表5可知，核函數數量U和步長過大或過小都會降低診斷精度，U=5及ζ=2時診斷結果最佳。由表6可知，當α<0.5時，增大α可以提高診斷精度；當α>0.5時，增大α則會降低診斷精度，而隨著訓練次數變化的αe診斷結果最佳。這是因為α過大會干擾標簽數據的訓練，過小會導致偽標簽數據無效果，而αe不僅可以解決以上問題，還可以避免局部最優。由表7可知，當λ<0.1時，增大λ可以提高診斷精度；當λ>0.1時，增大λ則會降低診斷精度，而隨著訓練次數變化的λe診斷結果最佳。這是因為λ的主要作用是平衡訓練過程中的訓練損失與子域分布差異，而λe可以抑制訓練早期的適配層噪聲。

為了證明1D-CNN模型在齒輪故障特征提取上的有效性，將其與ML-MK-I(multi-layer multi-kernel integrated objective)[11]、FTNN (feature-based transfer neural network)[12]和DTN-JDA(deep transfer network with joint distribution adaptation)[13]用于特征提取的CNN模型在數據集A上進行比較，結果如圖6所示。

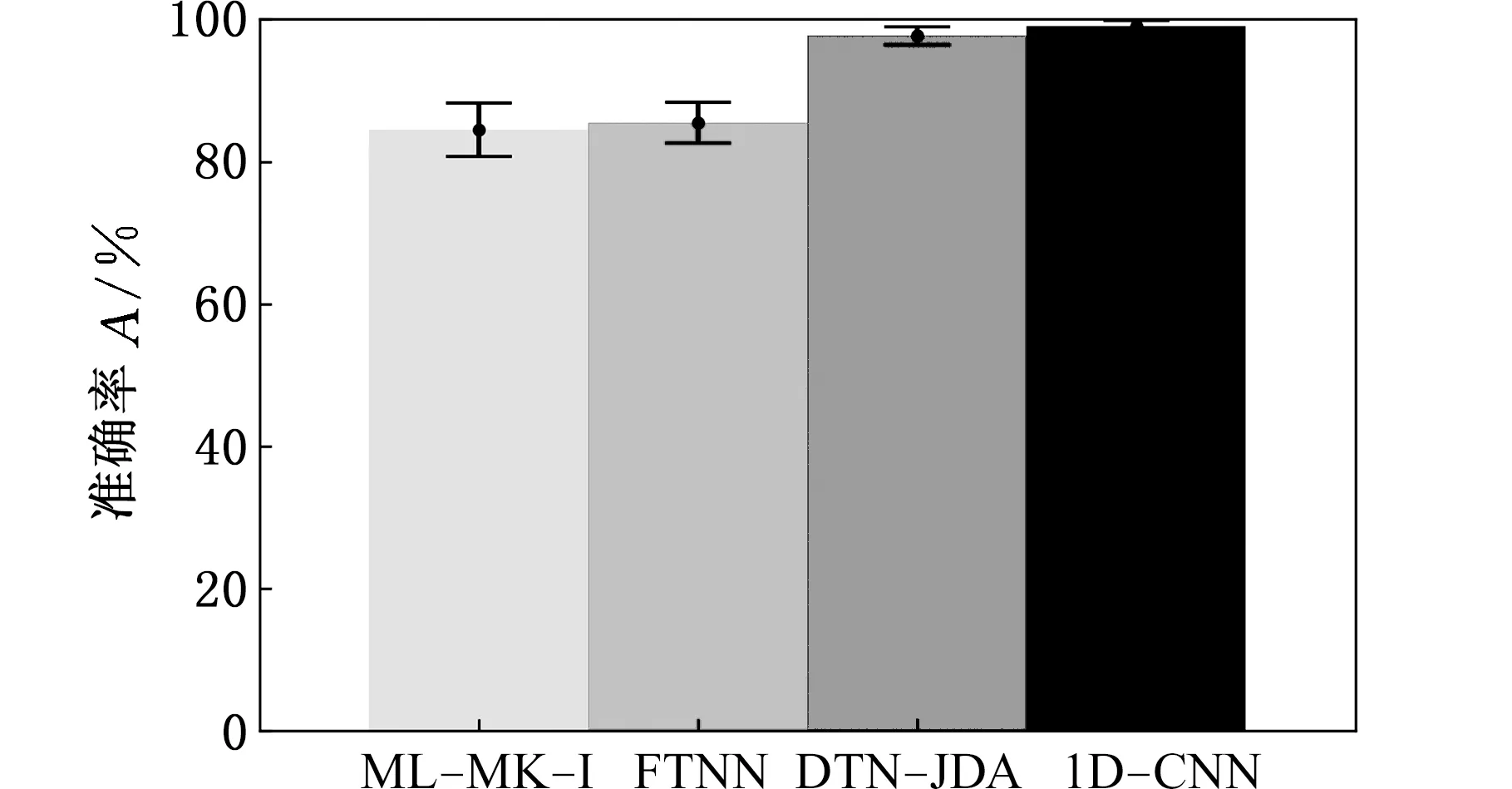
圖6 準確率對比圖Fig.6 Comparison diagram of accuracy

由圖6可知，ML-MK-I與FTNN的CNN準確率較低。其中，ML-MK-I的準確率為84.50%，FTNN的準確率為85.50%。這是因為它們的CNN結構較為簡單，且第一個卷積層的卷積核較小。而DTN-JDA的CNN與1D-CNN都采用寬卷積核和Dropout結構，其準確率較ML-MK-I與FTNN有了較大的提高，分別達到97.72%、99.02%，但通過查看DTN-JDA的訓練過程發現其完成模型訓練所需的計算資源遠大于1D-CNN的計算資源。這可能是因為DTN-JDA的第二個全連接層占用了較大的計算資源。綜上，1D-CNN模型較其他深度遷移學習方法的CNN網絡在齒輪故障特征提取上具有一定的優勢。

為了證明所提方法的優越性，將其與1D-CNN、基于1D-CNN的域適配網絡(1D-CNN-based domain adaptation network, 1D-DAN)、FTNN和DTN-JDA在遷移任務A→B、A→C與A→D上進行比較。其中，1D-CNN不進行特征的分布適配，1D-DAN只進行基于最大均值差異的域適配，結果如圖7和表8所示。

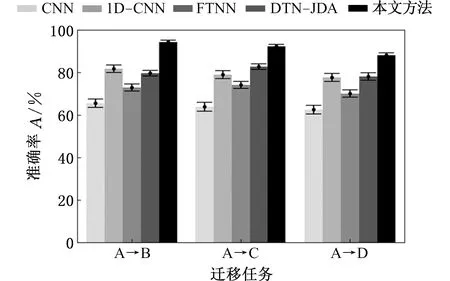
圖7 遷移結果對比圖Fig.7 Comparison diagram of transfer results

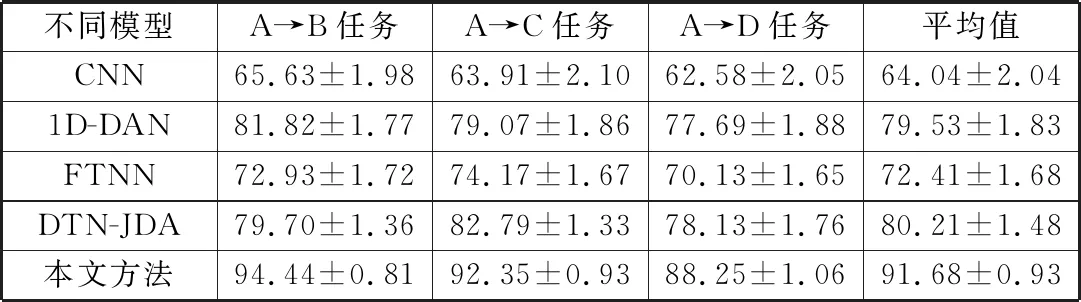
表8 遷移結果對比Tab.8 Comparison of transfer results

由圖7和表8可知，1D-CNN的準確率不高，僅為64.04%，這是因為1D-CNN雖可以提取出深層的可遷移特征，但缺少可遷移特征分布適配的過程，不能減小可遷移特征的分布差異。FTNN和DTN-JDA都進行了可遷移特征的分布適配，準確率較1D-CNN有了較大的提高。1D-DAN的準確率較1D-CNN有一定的提高，但低于本文方法，這是因為1D-DAN雖進行了可遷移特征的域適配，但其分類效果不及子域適配。對比遷移結果可知：

(1)相比其他方法，本文方法具有更高的遷移準確率。一方面是因為1D-CNN能夠提取出更為深層的可遷移特征；另一方面是子域適配可以同時減小可遷移特征的全局分布差異和子域分布差異。

(2)FTNN的特征提取網絡性能較差，難以提取深層的可遷移特征，而DTN-JDA將邊緣分布適配擴展到聯合分布適配，提高了分布適配的準確度，故遷移準確率從大到小排序為：本文方法，DTN-JDA，1D-DAN，FTNN，1D-CNN。

為了進一步對比分析不同診斷方法的差異性，使用t-分布隨機鄰域嵌入(t-distributed stochastic neighbor embedding,t-SNE)算法可視化1D-CNN、1D-DAN與提出方法在遷移任務A→D上的分類結果，以散點圖形式呈現，如圖8所示。

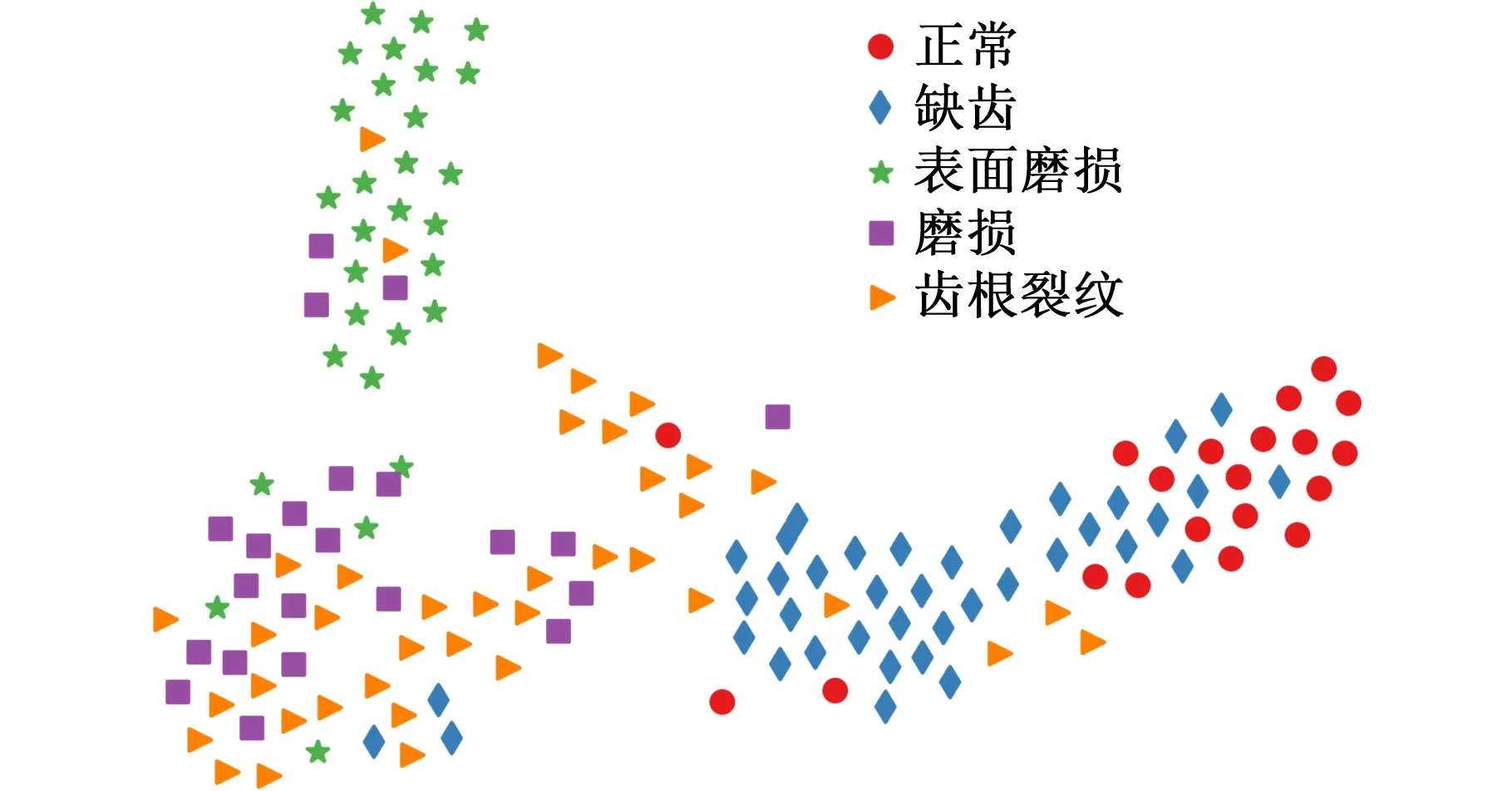
(a)1D-CNN

由圖8可知，1D-CNN沒有起到縮小故障特征的類內距離和增大類間距離的效果，故無法正確識別數據集D的健康狀況。而1D-DAN雖一定程度上縮小了故障特征的類內距離，但沒有增大類間距離，故存在錯誤分類的情況。本文方法在縮小數據集D故障特征類內距離的同時增大了類間距離，故分類效果較好。綜上，本文方法通過子域適配縮小了源域與目標域可遷移特征的類內距離，增大了類間距離，使模型能夠識別目標域的健康狀況，直觀地解釋了本文方法的有效性。

4 結論

(1)相比同類深度遷移學習方法的特征提取網絡，1D-CNN模型在齒輪故障特征提取上具有一定的優勢。

(2)子域適配能夠同時減小可遷移特征的全局分布差異和子域分布差異，顯著提高了識別精度。

(3)本文方法能在目標域無標簽的情況下識別目標域的健康狀態，使齒輪故障診斷能有效克服生產實際中變工況帶來的影響，提高了診斷的泛化性能。