基于二階對抗樣本的對抗訓練防御
錢亞冠 張錫敏 王 濱 顧釗銓 李 蔚 云本勝
①(浙江科技學院理學院/大數據學院 杭州 310023)
②(杭州海康威視網絡與信息安全實驗室 杭州 310052)
③(廣州大學網絡空間先進技術研究院 廣州 510006)
1 引言
深度神經網絡(DNN)在生物信息學[1,2]、語音識別[3,4]和計算機視覺[5,6]等領域獲得成功應用的同時,研究者們發現DNN容易受到對抗樣本的攻擊[7],即在自然圖像中添加微小的擾動,可以欺騙DNN做出錯誤預測。由于對抗樣本具有較好的隱蔽性,不易被人眼發現,給安全敏感的應用帶來很大的破壞性。例如,在自動駕駛領域,研究者們通過在道路交通標志圖片上添加微小擾動得到對抗樣本,導致采用DNN進行道路交通標志識別的自動駕駛汽車做出錯誤判斷,引起交通事故的發生[8]。自動駕駛系統可能會遇到的道路交通標志圖片及其對應的對抗樣本,對于人眼來說,兩張圖片是相同的,同為注意危險標志。而自動駕駛系統中的DNN則把對抗樣本判斷為讓行標志。這意味著難以察覺的擾動有可能使一輛毫無故障的自動駕駛汽車做出危險的行為。因此,對于對抗樣本的防御研究具有現實意義。
自Szegedy等人[7]發現DNN中存在對抗樣本以來,研究者們提出了一系列對抗樣本的生成與防御方法。生成對抗樣本的過程通常被建模為一個有約束優化的問題,其目標是在約束條件下最大化損失函數。現有的典型對抗樣本包括C&W[9], Deepfool[10],FGSM[11], PGD[12], M-DI2-FGSM[13]等。同時,研究者們提出了多種防御對抗樣本的方法,如防御蒸餾[14]、對抗訓練[15]、強化網絡[16]及對抗樣本檢測[17]等。
在大部分防御方法被文獻[18]證實防御效果有限的情況下,對抗訓練是少數被經驗證明為目前最為有效的防御方法。對抗訓練最早由Szegedy等人[7]提出,通過將對抗樣本注入訓練過程,以增強DNN的魯棒性。隨著研究的深入,Madry等人[13]將對抗訓練形式化為由內部最大化問題和外部最小化問題組成的鞍點問題,即存在對抗樣本最大化損失函數的情況下,優化模型參數實現損失函數最小化。按照Madry等人的鞍點理論,解決內部最大化問題需要更強的對抗樣本,他們提出了基于PGD(1階梯度投影)的對抗訓練方法,實驗證明能夠防御大部分1階梯度攻擊。但是1階梯度對于DNN的逼近能力有限,無法進一步找到更強大的對抗樣本,因而也無法訓練出更魯棒的DNN。基于這個思路,本文提出于基于2階梯度的對抗樣本生成方法。與以往線性逼近方法不同,在輸入樣本的微小鄰域內,對DNN損失函數進行2階多項式逼近。本文提出的方法優點是,利用Hesse矩陣可提取到損失函數在輸入鄰域內的更多信息,從而更好地解決內部最大化問題。
本文分別從理論和實驗角度證明了2階對抗樣本強于PGD對抗樣本。本文提出將對抗樣本的擾動下界,即攻擊成功所需的最少擾動,用于衡量不同對抗樣本的強度。計算結果顯示,2階對抗樣本的擾動下界低于PGD,即2階對抗樣本攻擊成功所需的最少擾動少于PGD,這意味著2階對抗樣本強于PGD。在MNIST和CIFAR10上的實驗結果驗證了本文的理論分析:(1) 相較于包括PGD在內的現有典型對抗樣本,2階對抗樣本能夠在添加更少擾動同時,達到更高的攻擊成功率;(2) 基于2階對抗樣本的對抗訓練能夠防御現有的典型1階對抗攻擊。
2 預備知識
2.1 深度神經網絡

2.2 對抗樣本

2.3 威脅模型
目前有很多對抗樣本的生成方法,但這些方法都是在一定的假設限制下進行的[9]。由于對手的攻擊行為很大程度上決定了對抗樣本的強度。如果攻擊行為不被限制,對手甚至可以使用任意圖像替換給定的圖像,這就違背了對抗樣本的定義。為此,我們把這些攻擊行為定義為威脅模型,通常包含攻擊目標和攻擊能力。
(1) 攻擊目標
威脅模型中的攻擊目標可以被定義為一個需要被檢測和防御的具體式子。在DNN中,對于攻擊目標的劃分有利于我們明確這個具體式子。因此,威脅模型中,對于攻擊目標的劃分至關重要。可以將攻擊目標具體劃分為2類,包括無目標攻擊和有目標攻擊。無目標攻擊是指改變對抗樣本的類別至任意一個非正確類。有目標攻擊是指改變對抗樣本的類別至指定的一個非正確類。正式地說,有目標攻擊是無目標攻擊的一個子集,而對于對抗樣本的防御方法來說,防御兩者的難易程度并不會有所區別。因此,本文提出的2階對抗樣本屬于目前更為主流的無目標攻擊。
(2) 攻擊能力
對抗樣本還可以根據對手掌握目標分類器信息的多少來定義攻擊能力,分為白箱攻擊和黑箱攻擊。白箱攻擊是指攻擊者幾乎知道關于DNN的所有信息,包括訓練數據、激活函數、拓撲結構、權重系數等。黑箱攻擊則假設攻擊者無法獲得已訓練的DNN內部信息,僅能獲得模型的輸出,包含標簽和置信度。因為需要掌握目標DNN的梯度信息,2階對抗樣本屬于白箱攻擊。
3 對抗訓練防御方法
3.1 問題的提出
目前最有效的對抗訓練方法是由Madry等人[13]提出的PGD對抗訓練。從優化的觀點出發,對抗訓練被定義為關于鞍點的優化問題:

可以發現式(3)是一個內部最大化問題和一個外部最小化問題的組合。內部最大化問題是找到令DNN產生最大損失的對抗樣本。外部最小化問題是在某種對抗攻擊下,尋找使對抗損失最小的模型參數。由此可見,對抗訓練是模型精度和魯棒性之間的一種最佳平衡。Madry等人[13]認為存在更強大的對抗樣本可以更好地解決內部最大化問題,從而訓練出更加魯棒的DNN,但基于一階對抗樣本不能很好地解決這個問題。為此,本文提出2階對抗樣本解決式(3)中的內部最大化問題。
3.2 2階對抗樣本
本節給出了一種對抗樣本的2階生成方法。我們將生成對抗樣本的過程定義為一個箱約束的優化問題:


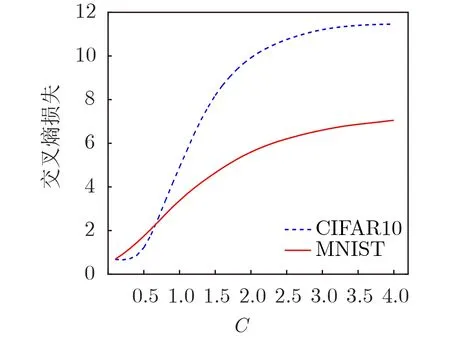
圖1 C與優化過程中交叉熵損失函數的關系

表1 基于2階對抗樣本的對抗訓練算法

4 理論分析




5 實驗
通過實驗進行驗證:(1)相比于以C&W, Deepfool, FGSM, PGD以及M-DI2-FGSM為例的典型對抗樣本,2階對抗樣本在具有更高隱蔽性的同時具有更高攻擊成功率;(2)相比于PGD對抗訓練,基于2階對抗訓練抗御對當前典型對抗樣本都具有魯棒性且具有更高的分類準確率。
5.1 實驗設置
本文實驗的數據集為MNIST和CIFAR10。MNIST是一個包含從數字0到9的10個類的手寫體數據集,共包含70000張手寫體數字圖像,每個圖像的大小為 2 8×28像素。實驗選取60000張圖像作為訓練數據,10000張圖像作為測試數據。CIFAR-10數據集由60000個 32×32彩色圖像組成,包含10個類。實驗選取50000個圖像作為訓練數據和10000圖像作為測試數據。訓練集分為5個訓練批次,每個批次有10000個圖像。對于MNIST我們使用精度為98.79%的標準LeNet網絡。對于CIFAR10我們使用精度為76.97%的標準AlexNet網絡。
5.2 評估指標
實驗使用4個評估指標,包括?2,?∞,PSNR以及ASR。現有的研究普遍用?2的值來衡量全局添加的擾動量,?∞來衡量局部(單個像素)添加的擾動量。峰值信噪比(PSNR)作為最廣泛使用的評價圖片質量的客觀度量,可以對對抗樣本的隱蔽性進行有效評估。ASR稱為對抗樣本的攻擊成功率,目前被大多數文獻用于衡量攻擊能力。若生成對抗樣本的成功率不是100%,那么這些數據僅取了成功的那部分作為基數。
5.3 評估2階對抗樣本
本文采用機器學習模型攻防庫Cleverhans[19]中的C&W,Deepfool,FGSM,以及由原作者給出代碼的PGD和M-DI2-FGSM作比較實驗。為保證評估的嚴謹性,實驗采用相同模型架構和測試數據集。其中,C&W的擾動上限δ=0.3 ,ε=0.3,學習率為0.1;Deepfool的參數設置與C&W相同;而FGSM作為單步迭代法,ε=0.3;PGD作為FGSM的衍生方法,迭代擾動固定為ε=0.3;M-DI2-FGSM中,ε=0.3。
實驗中,從MNIST與CIFAR中隨機取出500張可以被DNN正確判斷的圖片進行測試,實驗結果如表2所示。實驗證明,在不同數據集中,相比于現有的典型攻擊方法,2階對抗樣本不但攻擊成功率更高,而且添加的擾動更少。

表2 不同的對抗樣本在MNIST和CIFAR10的對比
5.4 對抗訓練2階對抗樣本
本文分別采用自然樣例、2階對抗樣本,C&W,Deepfool, M-DI2-FGSM, FGSM以及PGD進行攻擊和對抗訓練,用于對比攻擊效果與防御效果。從MNIST與CIFAR10中隨機取出200張可以被初始模型正確判斷的圖片進行測試。圖2是實驗結果的熱力圖表示,橫軸表示各種方法產生的對抗樣本,縱軸表示用不同對抗樣本進行對抗訓練得到的對抗訓練模型,圖中每一個數字代表某一個對抗訓練模型對于某一類對抗樣本的分類準確率。圖2的結果表明:(1)對抗訓練產生的對抗訓練模型對于特定攻擊具有魯棒性;(2)相比于PGD對抗訓練,基于2階對抗樣本的對抗訓練防御能夠防御現存典型1階對抗樣本,且具有更高的分類準確率。

圖2 對抗訓練DNN對于對抗樣本的分類準確率
6 結束語
通過理論分析可知,2階對抗樣本的擾動下界低于1階最強對抗樣本PGD,表明2階對抗樣本強于PGD,能夠更好地解決對抗訓練的內部最大化問題。在MNIST和CIFAR10數據集上的實驗表明,相較于現有的典型1階對抗樣本,2階對抗樣本擁有更高的攻擊成功率和更高的隱蔽性。相比于PGD對抗訓練,基于2階對抗樣本的對抗訓練防御能夠防御現存典型1階對抗樣本,且具有更高的分類準確率。2階對抗樣本中參數經驗值的選取是通過大量實驗得到的,將來對參數的選取機制有待進一步研究。目前還未有研究者對對抗樣本的在線攻擊與線下攻擊進行分析,在未來的工作中,我們將進一步研究2階對抗樣本與其他對抗樣本在線攻擊與線下攻擊的不同特征。

