基于FPGA技術的雙磁控憶阻Shinriki振蕩器對稱行為分析
閔富紅 鄭宏亮 芮 智 曹 弋
(南京師范大學電氣與自動化工程學院 南京 210046)
1 引言
基于電路的完備性和基本變量的對稱性,1971年文獻[1]首次從理論上提出憶阻器的概念。作為一類具有記憶性的非線性二端口元件,憶阻器的伏安特性曲線常表現為斜“8”字型的過零點緊磁滯回線特征[2]。因此,將其與非線性混沌電路結合極易產生豐富的動力學現象。大量研究表明,憶阻混沌電路在神經網絡[3]、人工智能[4]、保密通信[5]、信號處理[6]等方面具有廣闊的應用前景。因此,多種憶阻電路[7]被相繼提出和分析,其中有憶阻超混沌Jerk系統[8]、非自治憶阻FitzHugh-Nagumo電路[9]、憶阻文氏橋振蕩器[10]和Sallen-Key低通濾波憶阻振蕩器[11]等。
不同于普通非線性電路,憶阻電路往往擁有更為復雜的動力學特性,比如,對稱分岔行為、多穩態特性、反單調性和不完全對稱行為等。對稱性[12]在關于初值對稱的憶阻系統中普遍存在,從系統方程中即可看出。而文獻[13]在改進型憶阻蔡氏電路中,首次發現了特定參數下系統的對稱分岔行為,并通過共存分岔圖和李雅普諾夫指數進行揭示。多穩態現象[14]主要表現為依賴于系統初始條件的多種吸引子共存現象。文獻[15]構造了基于最簡憶阻器的準哈密頓系統,系統無平衡點,但存在無窮多隱藏吸引子,在多穩態現象下揭示系統通過間歇和瞬態混沌走向混沌的途徑。反單調現象[16]是當某些特定參數或初值變化時,在參數域或初值域成對產生正向和反向倍周期分岔級聯的現象。文獻[17]討論了基于RLCM四元件的混沌電路中,隨參數變化出現的正負初值互補共存的周期-混沌氣泡。擁有不同拓撲結構吸引子的不完全對稱行為[18]通常存在于低維系統中,文獻[19]在3階憶阻HR神經元模型中運用相位圖、分岔圖和動力學地圖等分析方法,揭示了系統存在的不對稱共存吸引子的隱藏動力學行為。但是,關于特定參數的對稱動力學行為在高維系統中的研究較少。
基于此,本文通過在經典Shinriki振蕩器[20]中引入無源和有源磁控憶阻,并在電感支路串聯電阻,搭建出一個新型的5維憶阻振蕩系統。通過動力學行為分析發現該系統特有的在特定參數下的對稱共存分岔現象,并通過Lyapunov指數譜對比驗證。同時將這一現象延伸至雙參數平面以及參數-初值平面內分析,觀察到在對稱吸引域內多種運動狀態吸引子的共存行為。對系統在對稱域內伴隨出現的反單調現象、不完全對稱行為等進行了重點分析。最后,在FPGA數字平臺,對雙磁控憶阻Shinriki振蕩器開展電路實驗,通過仿真波形驗證數值分析的正確性以及對稱動力學行為的真實存在性。
2 雙磁控憶阻Shinriki振蕩器模型
圖1給出了雙磁控憶阻Shinriki振蕩器模型,電路結構主要由3個部分構成:負阻抗轉換器、非線性正電阻區域以及RLC諧振回路。原電路[20]中負阻抗轉換器由兩個等值電阻R1和R2、 運算放大器U以及接地電阻R3組成,該部分對外電路表現為?R3,且作為電源向電路其他部分供能。非線性正電阻區域利用一個3次無源磁控憶阻器W1替換原來的二極管串并聯支路。負阻抗轉換器與非線性正電阻區域間通過R4和電容C0的并聯連接在一起。RLC諧振回路的存在,對電路能隨機產生振蕩波形和周期性波形起到了關鍵作用,本文中,在電感L支路串聯電阻R5,同時將電阻支路用一個3次有源憶阻器W2替代,提高電路的復雜度,便于產生更豐富的非線性動力學現象。新構建的雙磁控憶阻Shinriki振蕩器包含5個動態元件,分別是電容C0,C,電感L,兩個磁控憶阻器W1和W2,對應的狀態變量如圖1所示為VC0,VC,iL,φ1和φ2。
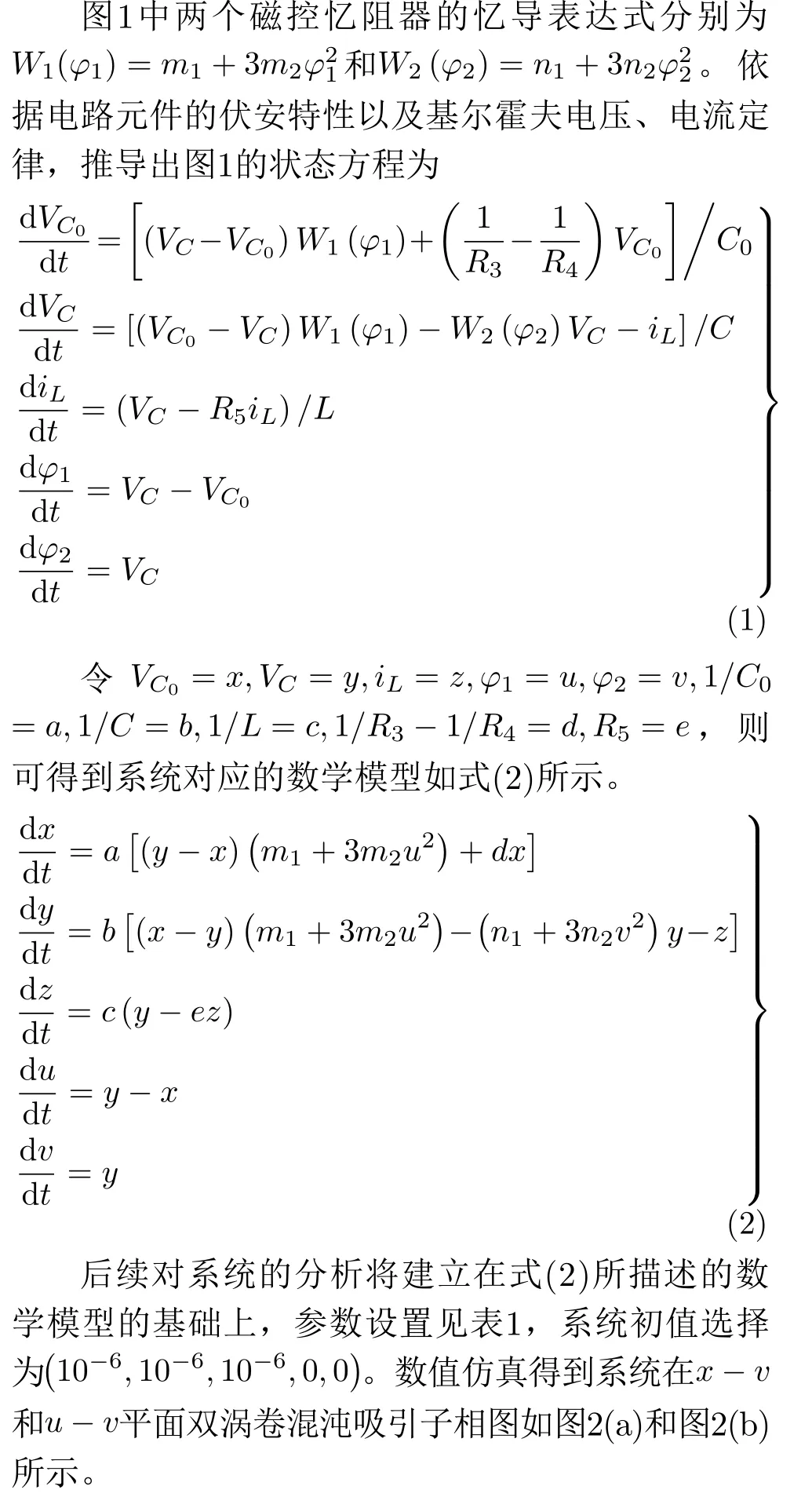
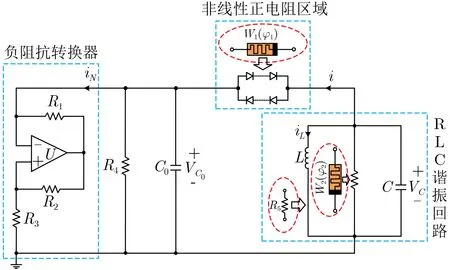
圖1 雙憶阻Shinriki振蕩器模型
3 動力學行為分析
3.1 對稱共存分岔行為
為了研究振蕩器式(2)在不同單參數變化時產生的分岔行為,給出系統隨參數c,d變化的共存分岔圖和Lyapunov指數譜如圖3所示。其中,參數c表示的是系統中電感L值的倒數,負電阻R3的倒數和正電阻R4倒 數的差值為參數d。 初值設置為(±10?6,±10?6,±10?6,0,0),固定其它參數如表1所示,在達到起振條件下弱化初值對系統的影響。

表1 系統參數設置值
在圖3(a)中,參數c的變化區間為( 14.6,23.8),可以觀察到隨著參數c取值的增加,系統先后遍歷了混沌態、周期窗、多周期,然后通過反倍周期分岔進入周期一,最后達到穩定不動點狀態,其中,周期窗和多周期狀態衍生穿插在混沌態之間。當參數c<14.484時,系統處于大周期狀態,對應狀態變量xmax躍變為極大的值,且最小Lyapunov指數L5驟降為極小的值,考慮到分岔圖和Lyapunov指數譜的協調性和可觀察性,該部分區間未在圖3(a)和圖3(b)中給出,后續的分析中會加以說明。在c ∈(14.484,16.31)∪(16.684,18.928)時,系統產生混沌吸引子,對應于圖3(c)中的最大Lyapunov指數L1>0 。觀察圖3(a)可以發現,當c位于區間(16.31,16.684)∪(18.928,23.68)時系統處于周期態,而在c>23.68 時 最大Lyapunov指數L1小于零,進入穩定不動點狀態。再來將目光聚焦到圖3(b)中,容易發現系統隨參數d變化的共存分岔軌跡與圖3(a)中隨參數c的變化規律呈現出對稱性。參數d由1.59開始增加,系統先后經歷了穩定點、倍周期分岔至混沌態、多周期、周期窗和大周期等運動狀態。結合圖3(d)的Lyapunov指數譜,將系統隨參數c,d變化的運動狀態與具體的區間分布列于表2中,直觀地展現兩個參數的對稱共存分岔行為。
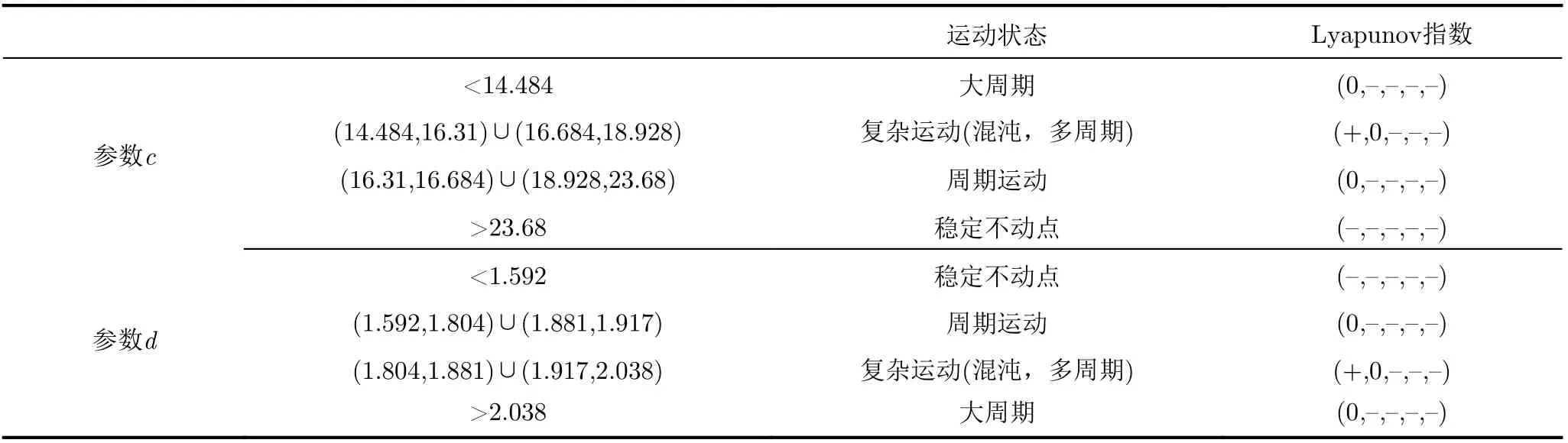
表2 振蕩器隨參數c, d變化時的運動狀態和對應Lyapunov指數

圖2 系統混沌相圖
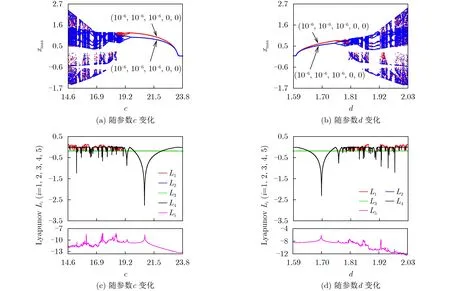
圖3 共存分岔圖和Lyapunov指數譜
3.2 雙參數平面內的對稱運動分布
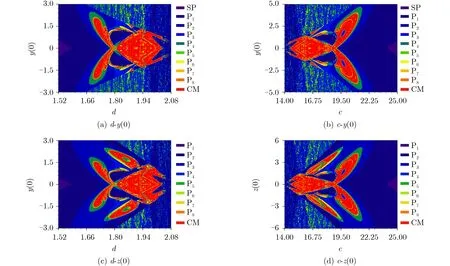
進一步探討系統參數對運動狀態對稱性分布的影響,繪制對稱參數和電容C的參數b以及有源磁控憶阻參數n2的雙參數圖如圖4所示。圖中不同顏色代表著不同狀態的動力學行為,“SP”指的是穩定不動點(Stable point),“P1~P8”表示的是周期1至周期8極限環(Period 1~Period 8),“CM”則代表著混沌、多周期等復雜運動(Complex motion)。
將圖4(a),圖4(b)與圖4(c),圖4(d)分為兩組,分別命名為組Ⅰ和組Ⅱ,容易看出同組中的動力學地圖呈現對稱分布。在組Ⅰ中,展現了在完整對稱參數域下與參數b的運動軌跡分布。參數d從1.52遞增至2.08的過程中,無論參數b取值如何,系統總是遍歷穩定不動點、周期、混沌和大周期4種運動狀態。相反地,當參數c∈(14.00,25.00)時,動力學行為分布先是從大周期到混沌,再過渡到周期,最終抵達穩定點。大周期狀態即為組Ⅰ中類似馬賽克的部分。為了更好地觀察周期與混沌態的共存情況,截取了部分對稱域與憶阻參數n2的組合得到組Ⅱ,消除了穩定點和大周期狀態。和組Ⅰ相比,運動狀態的遍歷性仍保持一致,且均具有多種運動狀態共存的特點。但是,組Ⅱ中憶阻參數經歷由負值到正值的轉變,表明憶阻元件由有源狀態切換為無源狀態,同時拓寬吸引域范圍,系統在多周期和混沌摻雜區域中運動狀態的切換更為頻繁,而且隨著憶阻參數的增大,多周期和混沌摻雜區的范圍逐漸減小。這些都表明了將憶阻元件引入混沌振蕩電路中,不僅可以保留原系統中固有的動力學行為,更能豐富其復雜的動力學現象。
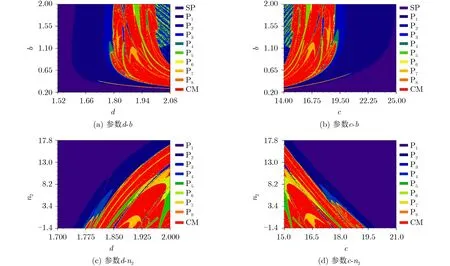
圖4 雙參數動力學地圖
3.3 依賴于對稱參數的初值域內聚合費根鮑姆樹現象
研究對稱參數對系統中存在的反單調行為的影響,該行為主要表現為成對出現的倍周期分岔和反倍周期分岔級聯現象,亦被稱為聚合費根鮑姆樹現象。圖5(a)~圖5(f)中記錄不同參數d下,狀態變量ymax隨初始條件z(0)變化的費根鮑姆樹分裂和聚合的過程。當d=1.65時,系統關于初值的對稱性,使z(0)在 區間(?4,4)內,左右分岔軌跡各出現周期2氣泡。在d增加至1.68后,左右周期2氣泡分支上小范圍內分裂出新氣泡,形成周期4氣泡。按此規律,繼續分裂出周期8氣泡。d=1.698時,周期8氣泡內出現混沌域,隨著d值增加,原來不接壤周期-混沌氣泡開始走向聚合,形成更大范圍內的周期-混沌氣泡串。
為驗證對稱參數在初值域內的反單調現象的對稱性,選擇6組和圖5相對應的參數c值,得到圖6(a)~圖6(f)中具有相同周期、混沌氣泡狀態的分岔軌跡圖。與參數d的遞增趨勢不同,圖6中展現的是隨c值減小,在初值z(0)區間內遍歷了周期2氣泡→周期4氣泡→周期8氣泡→8周期-混沌氣泡→4周期-混沌氣泡→2周期-混沌氣泡的氣泡吞吐過程。
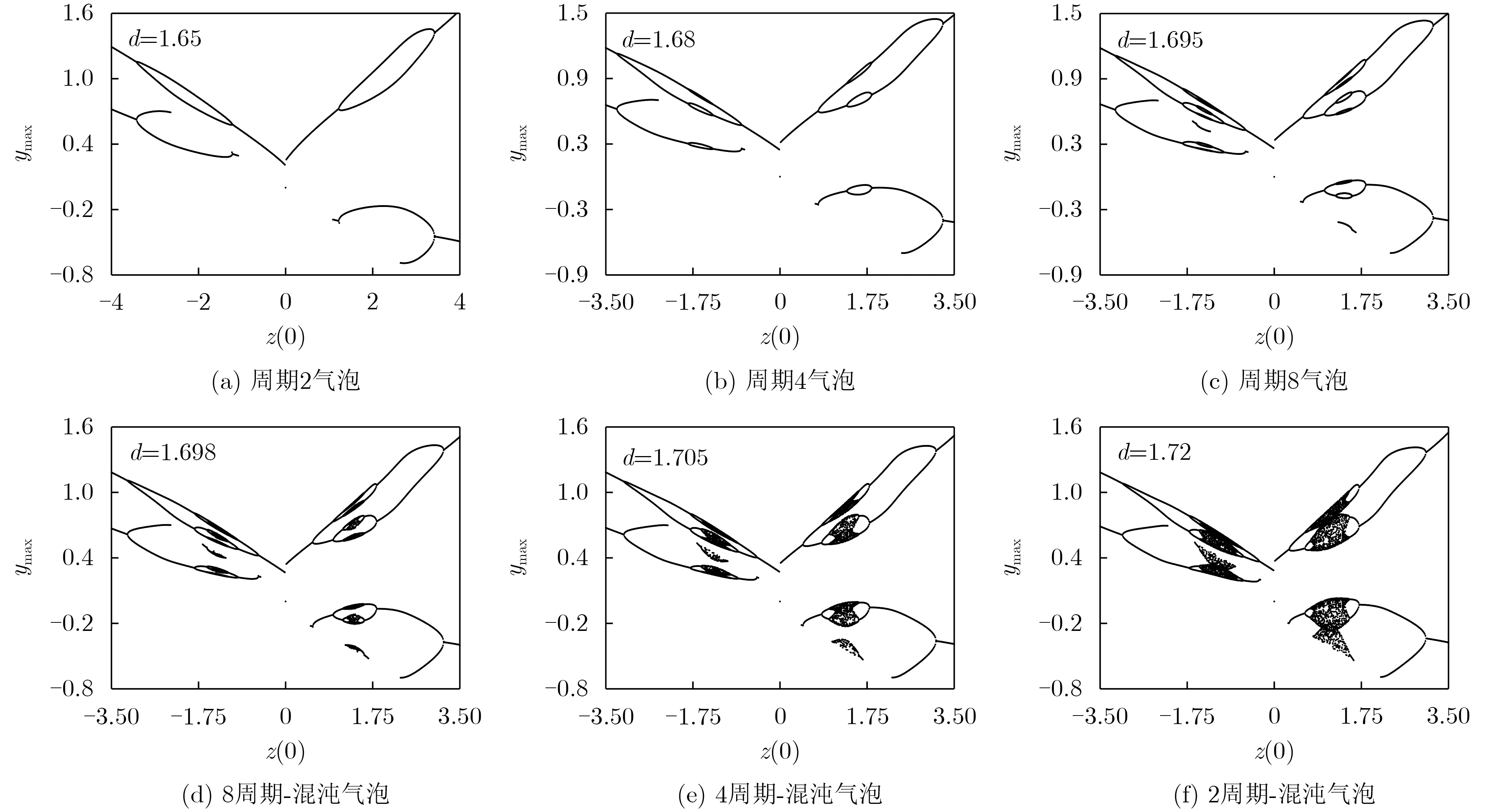
圖5 對稱參數d 決定的初值z (0)區間內聚合費根鮑姆樹現象
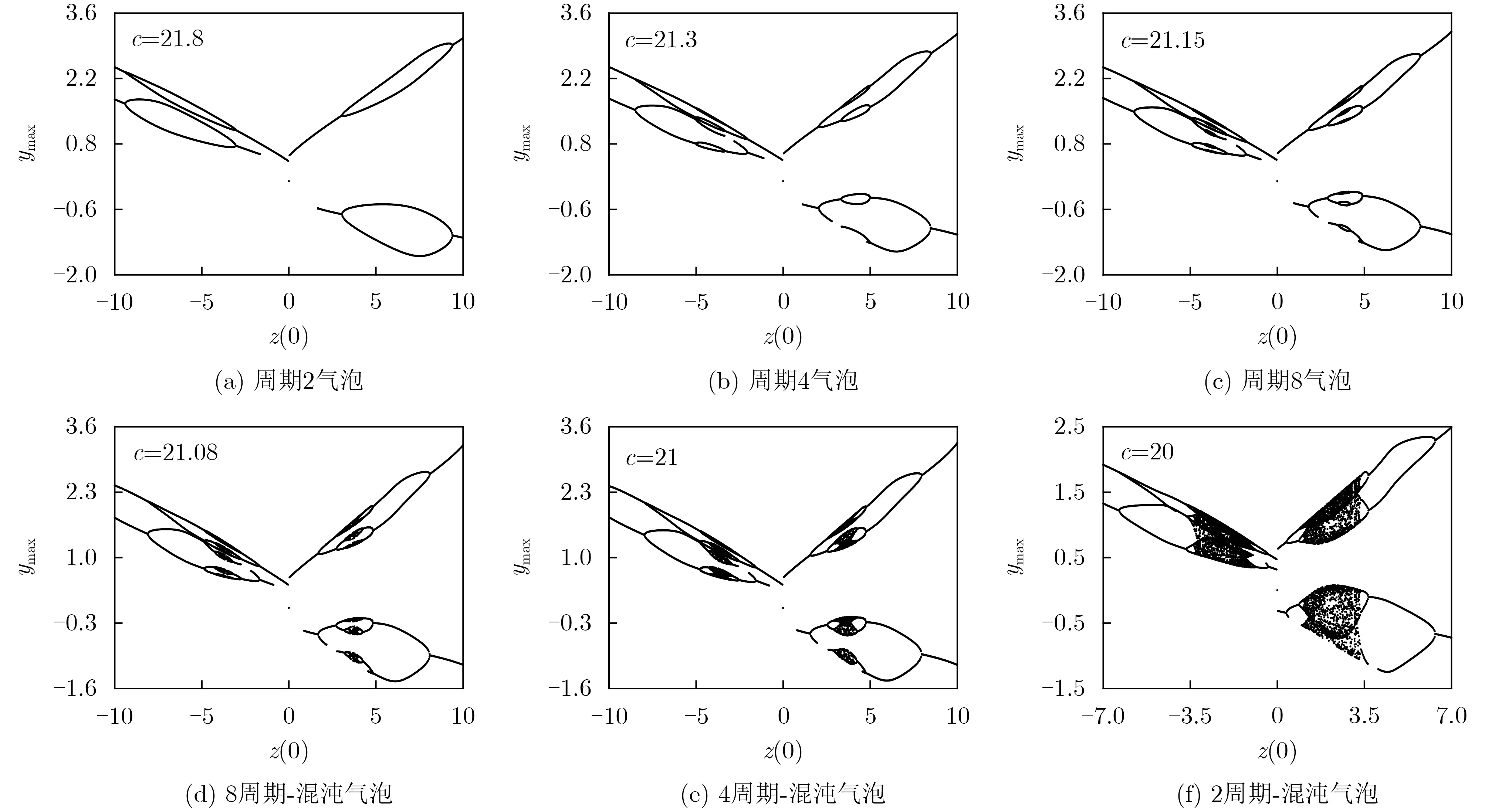
圖6 對稱參數c 決定的初值z (0)區間內聚合費根鮑姆樹現象
3.4 憶阻初值影響下的不完全對稱共存現象
分析在無源磁控憶阻初值u(0)的影響下,參數c區間內的不完全對稱共存現象。選擇u(0)=±0.2,參數c區間為( 15.1,21.9)時 ,得到狀態變量xmax的共存分岔圖和對應的前4根Lyapunov指數對比圖如圖7所示。圖7(a)中從初始條件(10?6,10?6,10?6,0.2,0) , ( 10?6,10?6,10?6,?0.2,0) ,(?10?6,?10?6,?10?6,0.2,0) 和(?10?6,?10?6,?10?6,?0.2,0)出 發的軌跡分別被標記為紅色、綠色、粉色和藍色。
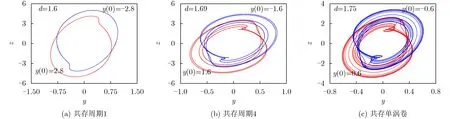
圖7(a)中,紅色和藍色軌跡互為平移關系,兩者在所選參數c區間內經歷的吸引子狀態具有一致性,從左至右依次經歷混沌、反倍周期分岔、周期-混沌氣泡、鞍結分岔,最終再一次反倍周期分岔從混沌走向周期1。豐富的動力學行為過程在圖7(b)中初值為正的Lyapunov指數譜上表現為譜線波動頻率高,系統內不斷發生運動狀態的切換。當初始條件中憶阻項和非憶阻項異號時,即綠色軌跡和粉色軌跡在參數區間內呈現的運動狀態相同,穩定點處軌跡重合,周期態處互為平移關系。截取參數c ∈(15.1,17.1)時兩軌跡對應的周期態放大圖見圖7(a)右下角,可以看出此時出現的是共存周期4氣泡。結合圖7(b),分析得出在初值同號和異號時,振蕩器在15.1 圖7 參數c 區間內共存分岔圖和Lyapnnov指數譜 研究在對稱參數c,d影響下參數-初值域內的對稱多穩態現象,數值仿真得到圖8中的兩組對稱參數d,c分別和兩個非憶阻狀態變量組合的“金魚”狀吸引盆平面。參數選擇見表1,圖8(a),圖8(b)中初值設置為 (0,y(0),0,0,0),類似地,圖8(c)和圖8(d)中為( 0,0,z(0),0,0)。 觀察圖8可以發現不同參數區間內的對稱性由參數域延續到初值域,無論是選擇參數或是初值,系統呈現出的獨特對稱性均取決于參數d, c。同時由于該系統自身在初值域固有的對稱性,即改變狀態變量的正負,系統的狀態方程始終保持不變,導致圖8中的多吸引子共存狀態均關于初值為0的界線上下對稱分布。圖8中的兩組圖分別在“金魚”頭部分完全對稱,而右半部分的圖中“金魚”翅和尾巴卻活躍在更為廣泛的初值區間內,分別和左半部分的兩張圖呈現出運動趨勢的相似性。造成這種現象的原因是憶阻電路具有依賴于初值的極端敏感性,而c是動態元件電容的參數,d對應的是靜態元件電阻的參數。當兩參數分別漸變時,動態參數更易刺激系統在更為寬廣的初值域內產生復雜的多種運動狀態吸引子共存現象。 為了驗證參數c,d在初值影響下的對稱多穩態現象。在圖8(a),圖8(b)中運動狀態相同的區域,各選取3組相反初值、參數取值不同的組合,數值仿真得到了系統在y?z平面中的多種運動狀態吸引子共存的相軌跡圖如圖9和圖10所示。 圖8 對稱參數與初值的吸引盆 圖9 參數d 和初值y (0)決定的共存相軌跡圖 圖10 參數c 和 初值y (0)決定的共存相軌跡圖 考慮利用FPGA技術平臺進行數字電路實驗,對振蕩器的數值仿真結果進行驗證。不同于一般焊接電路在調節參數和設定初值上難以控制誤差,FPGA平臺中功能的實現主要依賴于編程,使得系統參數的更改和初值的設置更為方便精準,適用于實現對參數及初值極端敏感的憶阻混沌電路。 雙憶阻Shinriki振蕩器的整體程序設計分為4個模塊,分別是module_DMSO, module_4RK,module_XB和module_DA模塊。其中,第1個模塊為頂層模塊,其它3個模塊為底層模塊。module_DMSO作為頂層模塊控制并依次調用其它3個底層模塊,按順序重復調用module_4RK和module_XB模塊,module_DA模塊的作用是將32位浮點數轉化為定點數輸出,最終在示波器上顯示相應的波形圖。 FPGA實驗的實物連接圖和不同平面上的混沌吸引子相軌跡圖如圖11所示。圖11(b)中的混沌相圖分別對應圖2(a),圖2(b)中的數值仿真結果。此外,為了驗證對稱參數在初值域內的多穩態現象,選擇圖9的相軌跡圖一一進行驗證得到圖12,參數選擇和初值設定參照圖9。通過FPGA數字電路實驗,證明了所構雙磁控憶阻Shinriki振蕩器的物理可實現性,而電路實驗結果和數值仿真的一致性,既證明了系統存在多運動狀態吸引子共存的多穩態現象,也從側面佐證了特殊參數下動力學行為呈現對稱性分布的正確性。 圖11 FPGA數字電路實驗結果 圖12 多穩態相軌跡圖驗證,CH1=200 mV, CH2=1 V 本文利用無源磁控憶阻替換經典Shinriki振蕩器中的串并聯二極管支路,再將RLC諧振回路中的電阻用有源磁控憶阻取代,并在電感支路串聯電阻,構造出擁有復雜電路結構的改進型雙磁控憶阻Shinriki振蕩器。通過觀察特定參數對應的共存分岔圖和李雅普諾夫指數譜,發現該振蕩器中存在獨特的對稱分岔運動。之后通過雙參數運動分布圖再次驗證了系統對稱運動狀態的存在性。在對稱參數與非憶阻初值組合的吸引盆中分析了對稱域中的多穩態特性,同時發現了對稱域內系統的反單調性和依賴于初值的不完全對稱行為。最后,基于FPGA技術對雙磁控憶阻Shinriki振蕩器進行了數字化實驗,從示波器中觀察到系統不同狀態下的共存吸引子,既驗證了數值仿真的正確性,也突出系統對稱運動狀態分布的存在性。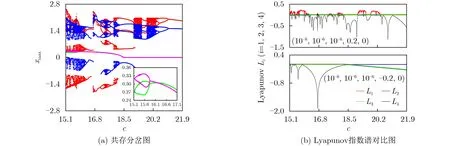
3.5 對稱域內的多穩態現象

4 基于FPGA數字技術的電路實驗


5 結論

