局部有源憶阻器電路及其在HR耦合神經元網絡中的應用
孫 亮 羅 佳 喬印虎
①(池州職業技術學院機電與汽車系 池州 247000)
②(安徽科技學院機械工程學院 鳳陽 233100)
1 引言
憶阻器被認為是繼電阻、電容和電感之后的第4種基本電路元件,它表征了電荷與磁通之間的本構關系,具有納米尺寸、非線性、低功耗和非易失性等特點。1971年,美國華裔科學家Chua教授[1]從數學對稱性出發提出憶阻器理論并預測了它的存在性,2008年美國惠普實驗室首次發現單個納米級TiO2憶阻器件[2]。此后,許多不同的器件被確定為憶阻器,并提出了不同的應用,特別是憶阻器用于模擬生物突觸[3-5]。
局部有源被認為是復雜性的起源,與生物神經突觸具有密切聯系[6,7]。2014年Chua教授[8]首次提出局部有源憶阻概念并設計了第1個局部有源憶阻器模型。2017年局部有源憶阻器被實驗室證實[9]。局部有源憶阻器比無源憶阻器具有更加復雜的動力學特性,具有更加廣泛的應用。近年來,一些局部有源憶阻器模型已經被提出和應用。例如,2018年Jin等人[10]提出一個局部有源憶阻器并與電容、電感電路組合實現了最簡單的混沌電路。同年,Chang等人[11]實現了一種雙穩態雙局部有源憶阻器。2019年,Weiher等人[12]進一步從材料物理實驗的角度證明了局部有源憶阻器的存在性。2020年,文獻[13,14]首次把局部有源憶阻器引入人工神經元模型中,并提出了局部有源憶阻神經元模型。盡管一些局部有源憶阻器已經被報道,但是局部有源憶阻器因為數學模型復雜、有源區間小等缺點很難在人工神經網絡中應用。生物神經系統具有豐富且復雜的放電活動,了解神經元以及神經元網絡的放電動力學機制有助于人工智能的發展,在過去的幾十年中已經吸引了大量的研究人員[15,16]。Hindmarsh-Rose (HR) 神經元具有簡單的數學模型[17],能夠模擬周期尖峰和簇發等多種神經元放電[18,19]。2019年Bao等人[20]使用一個無源憶阻器模擬兩個HR神經元之間的連接突觸,提出了基于憶阻突觸耦合HR神經元網絡,并分析了其同步動力學機制。
本文設計了一種簡單的局部有源憶阻器模型,不僅數學表達式簡單,物理電路實現容易,而且非常適合于模擬生物突觸。使用該局部有源憶阻器模擬兩個HR神經元之間的連接突觸,構建了一種局部有源憶阻突觸耦合的HR神經網絡。這種局部有源憶阻突觸耦合HR神經網絡能夠產生多種尖峰放電模式以及復雜的混沌行為。同時為了促進工程應用,設計了該局部有源憶阻器及其耦合神經網絡的等效實現電路,并由電路仿真驗證了數值仿真的正確性。
2 局部有源憶阻器
2.1 數學模型
根據憶阻器理論,一個廣義的壓控憶阻器可以表示為[21]
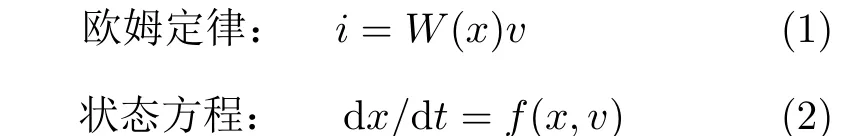
其中,W(x)是一個以x為變量的連續函數,稱為憶導,v, i, x分別表示施加在憶阻器兩端的輸入電壓,通過憶阻器的輸出電流,和憶阻器的內部狀態變量。基于式(1)和式(2),一個新的局部有源憶阻器模型能夠被設計,它的表達式為
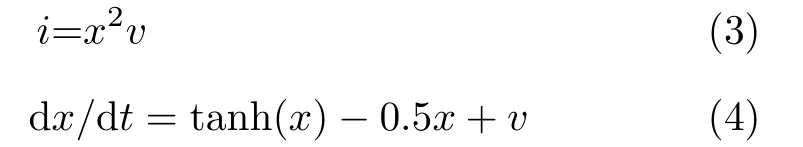
其中,x是憶阻器的內部狀態變量,表示磁通,tanh(.)是雙曲正切函數。
2.2 伏安特性
根據憶阻器理論[21,22],任意憶阻器應該具有以下3個特征:(1) 在雙極性周期信號的驅動下,假設存在周期響應,該器件在電壓-電流(v-i)平面中必須表現出過原點的收縮緊磁滯回線;(2) 從某個臨界頻率開始,緊磁滯回線波瓣面積應隨著激勵頻率的增加而單調減小;(3) 當頻率趨于無窮大時,收縮緊磁滯回線應收縮為單值函數。
當在局部有源憶阻器兩端施加雙極性周期激勵信號v=Asin(2πFt)時,不同的激勵信號幅度和頻率對憶阻器的作用被研究。例如,當設置激勵信號頻率F=2,初始狀態x(0)=0時,改變不同的信號幅度A所得到的伏安特性如圖1(a)所示。從圖1(a)可以看到,3個緊磁滯回線都通過v-i平面的0點,且幅度越大緊磁滯回線面積越大。當設置激勵信號幅度A=2,初始狀態x(0)=0時,調節不同的信號頻率F所得到的伏安特性曲線如圖1(b)所示。由圖1(b)可見,3個緊磁滯回線都通過v-i平面的0點,且隨著信號頻率的增加,憶阻器的緊磁滯回線面積越來越小,逐漸趨向于一條直線。顯然,所提憶阻器模型具有憶阻器的3個特征,是一種憶阻器件。

圖1 輸入信號幅度/頻率相關的伏安特性曲線圖
2.3 局部有源性
根據局部有源理論[8],如果一個憶阻器的直流(Direct Current, DC) 電壓-電流V-I 曲線存在負的斜率部分,那么該憶阻器就是局部有源的。為了證明所提出的憶阻器是局部有源憶阻器,它的局部有源特性被分析如下:
首先令憶阻器狀態方程dx/dt=0,可以得到它的平衡點狀態方程
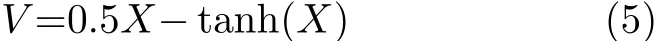
其中,V表示直流輸入電壓,X是滿足dx/dt=0時的x的解。然后再把式(5)替換到式(3)中得到輸出電流為
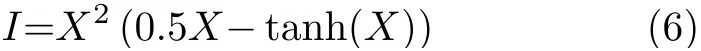
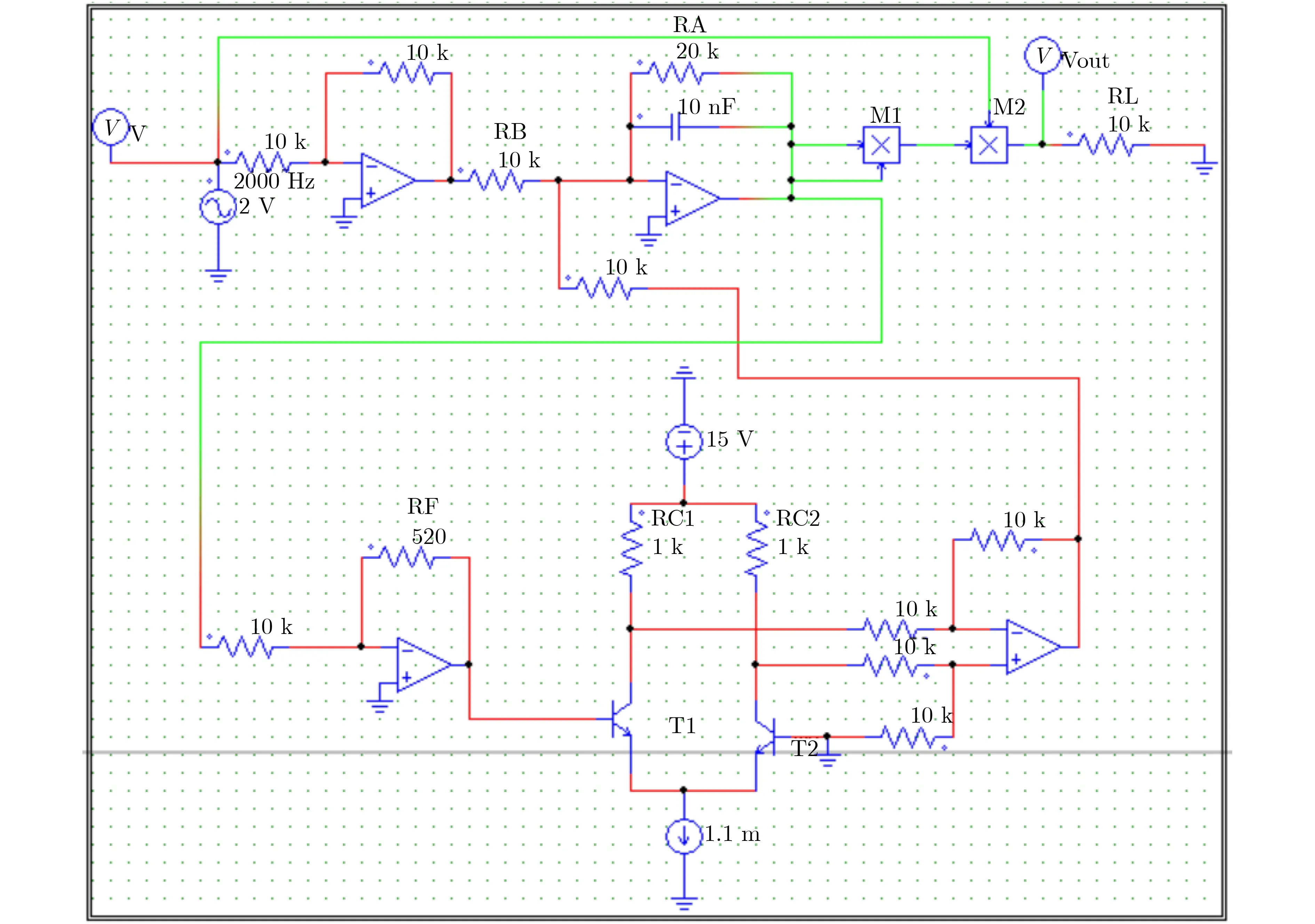
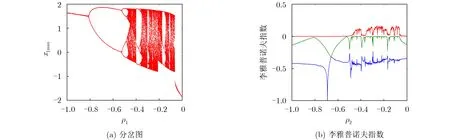
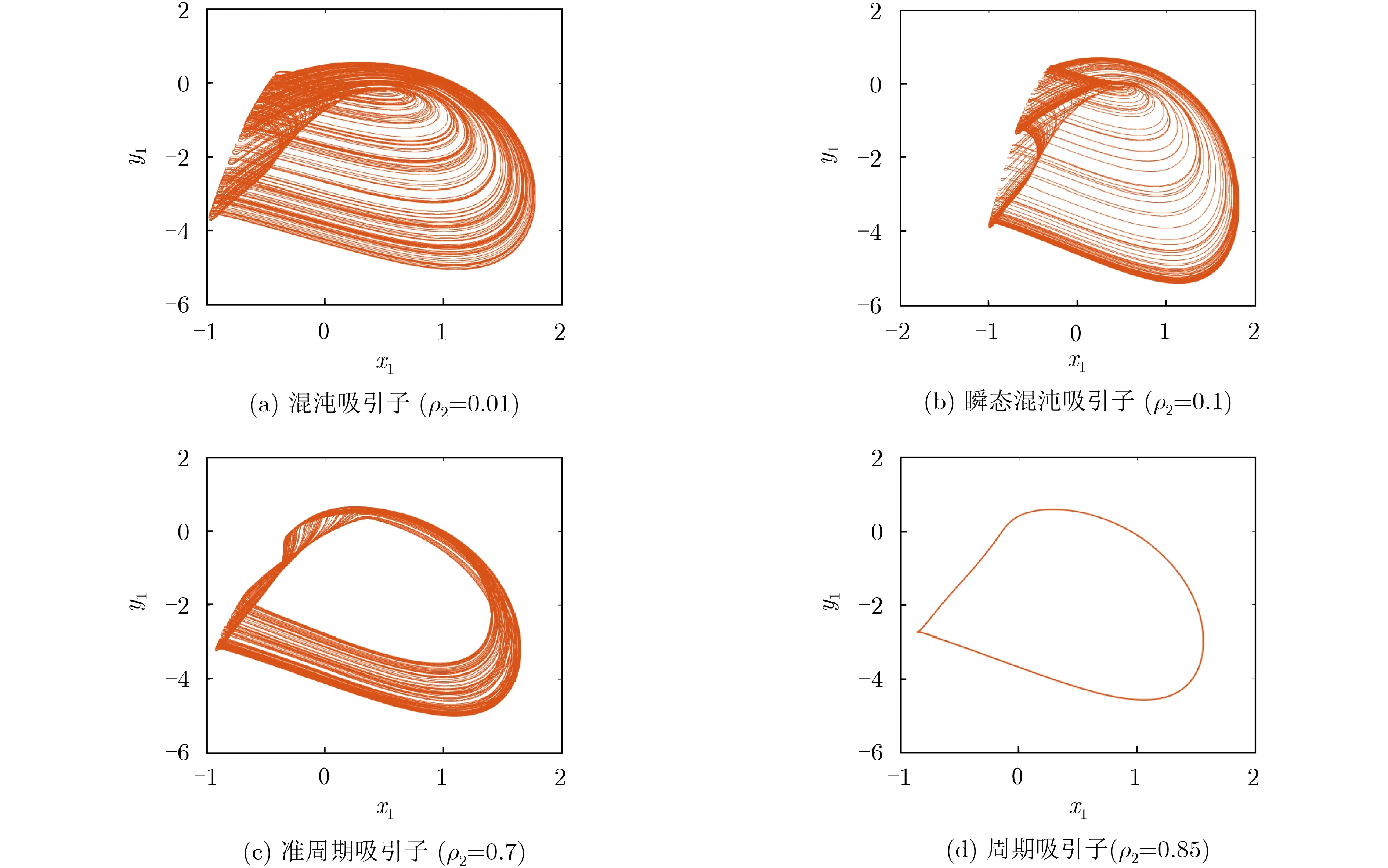
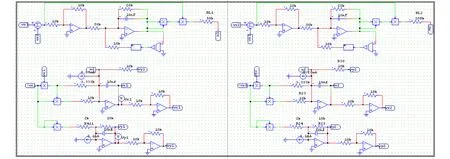
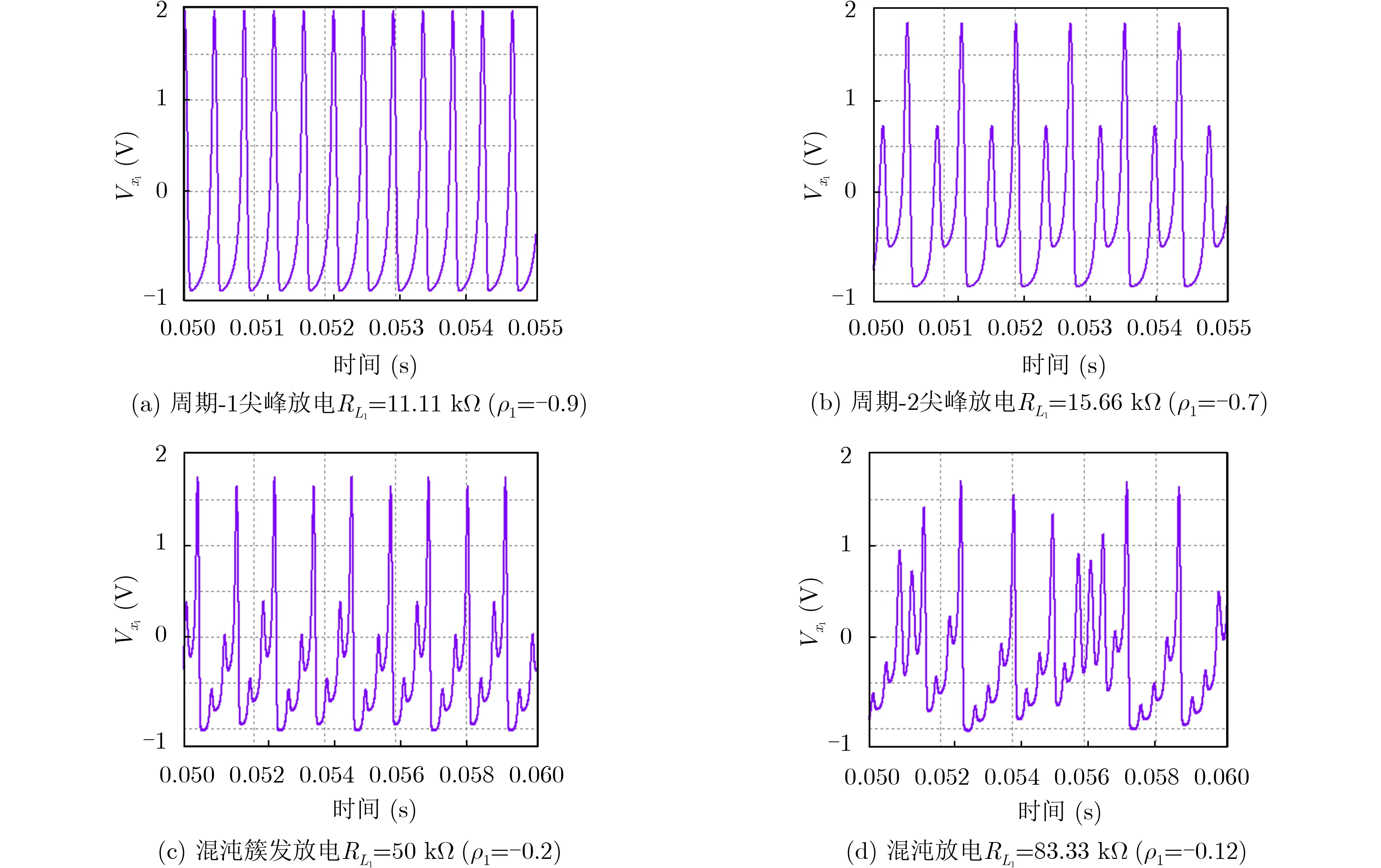
基于式(5)和式(6)可以得到憶阻器的DC V-I曲線,如圖2所示。由圖2可知,憶阻器的DC V-I曲線存在兩個對稱的負斜率區間,分別是0.89 圖2 局部有源憶阻器的DC V-I圖 基于式(3)、式(4)局部有源憶阻器模型,可以實現它的等效電路,如圖3(a)所示。其中,U是模擬運算放大器,M是模擬乘法器。雙曲正切函數使用文獻[14]所提出的雙曲正切電路實現,如圖3(b)所示。在雙曲正切電路中,當直流供電為±15 V,R=10 kΩ, RF=520 Ω, RC=1 kΩ, Io=1.1 mA時,電路能夠實現vo=-tanh(vi)。憶阻器內部狀態通過積分器的輸出電壓表示。根據基爾霍夫定律,局部有源憶阻器的電路方程可表示為 根據基爾霍夫定律,憶阻器數學模型式(3) i=x2v在憶阻器仿真器中對應的關系為i=(g2vz2v)/RL。其中,v和i分別表示輸入電壓和輸出電流,g=1為模擬乘法器的增益,vz為積分器輸出電壓,表示憶阻器內部狀態變量x,RL為可調匹配電阻。令R=10 kΩ, C=10 nF,根據積分時間常數RC=τ,可求得RL=g2R=1 0 k Ω, RA=R/0.5=2 0 k Ω,RB=R/1=10 kΩ。為了驗證數值仿真,在功率模擬(Power SIMulation, PSIM)電路仿真軟件中創建圖3所示電路,如圖4所示。為了方便測量憶阻器的輸出電流,在仿真時把RL接地。 圖3 電路圖 圖4 憶阻器PSIM仿真電路圖 對于數值仿真輸入電壓源v=Asin(2πFt)所對應的電路實驗輸入電壓源v=Asin(2πft),其中f=F/RC。因此,當數值仿真中F=2時,電路仿真頻率f=20 kHz,不同的電壓幅度仿真結果如圖5(a)所示。當A=2時,不同的電壓頻率仿真結果如圖5(b)所示。顯然,圖5的電路仿真結果與圖1的數值仿真結果基本一致。 圖5 局部有源憶阻器電路PSIM仿真結果 人類大腦包含了數以億計的神經元,它們通過突觸互相連接組成強大的神經網絡。突觸在神經網絡中不僅是物理連接,而且對于神經元之間的電信號傳輸起著關鍵的作用。由于憶阻器具有類似突觸的納米級、可塑性、非線性和非易失性等特點,可以使用憶阻器模擬神經突觸來開發等效的憶阻神經電路[23,24]。憶阻神經電路具有豐富的類腦放電動力學,利用憶阻器重構神經電路已經成為重要的研究課題。2維的HR神經元模型能產生豐富的尖峰和簇發放電行為,非常適合神經動力學的研究,其數學模型為[17] 其中,x是神經元的細胞膜電位,y是恢復變量,a,b, c, d是神經元模型參數。當使用局部有源憶阻器模擬兩個HR神經元之間的神經突觸時,兩個神經元之間的膜電位差的改變將引起磁通的變化,從而產生電磁感應電流。此時,膜電位與突觸的耦合可以使用憶阻器來描述[20]。因此,局部有源憶阻突觸耦合HR神經元網絡模型能夠被建立,如圖6所示。當兩個HR神經元通過局部有源憶阻器耦合時,由于兩個神經元之間的膜電位差x1-x2不斷改變從而產生磁感應電流,感應電流可以通過憶阻器表征為ρ1(x1-x2)W。當這個磁感應電流分別作用在兩個神經元上時,可以得到 圖6 局部有源憶阻突觸耦合神經元網絡結構圖 其中,ρ1, ρ2表示憶阻突觸耦合強度,x1和x2分別表示神經元1和神經元2的膜電位,x1-x2表示兩個神經元的膜電位差,y1和y2分別表示兩個神經元的恢復電位,憶導W=z2表示突觸權重,參數σ表示磁通泄露系數。 根據參考文獻[13]的定義,神經放電模式一般可以分為周期的尖峰和簇發放電,隨機的尖峰和簇發放電,混沌的尖峰和簇發放電以及混沌放電模式。當保持模型參數a=1, b=3, c=1, d=5, I1=-0.5, I2=-2.5, σ=0.2不變,兩個不對稱憶阻突觸耦合參數ρ1,ρ2作為可調參數時,局部有源憶阻突觸耦合HR神經元網絡動力學行為被研究。設置ρ2為0.1,初值為(0.2, 0.2, 0.2, 0.2, 0.2),當憶阻突觸耦合強度ρ1在區間[-1, 0]中逐漸增大時,系統的分岔圖和相應的李雅普諾夫(Lyapunov)指數譜可繪制如圖7所示。從分岔圖中可以看到,系統隨著耦合強度的增加,產生了多次正向周期倍分岔現象,在ρ1=-0.46時第1次由周期尖峰放電進入混沌放電后又多次以切分岔路徑退出混沌再次通過周期倍分岔進入混沌狀態。形成了多個不同周期放電的周期窗口。最后,在ρ1=-0.06時系統進入靜默狀態。圖7(b)中李雅普諾夫指數譜驗證了分岔圖的正確性。圖8給出了不同耦合強度ρ1時,系統的不同動力學行為時序圖。從圖8可見,局部有源憶阻突觸耦合HR神經元網絡能夠產生周期-1尖峰放電、周期-2尖峰放電、隨機尖峰放電、混沌簇發、混沌放電等多種放電模式。 圖7 關于憶阻突觸耦合強度ρ1動力學狀態分布 圖8 不同憶阻突觸耦合強度ρ1所對應的多種放電模式 設置ρ1為-0.4,初值為(0.2, 0.2, 0.2, 0.2,0.2),當憶阻突觸耦合強度ρ2在區間[0, 1]中逐漸增大時,系統的分岔圖和相應的李雅普諾夫指數譜可繪制如圖9所示。從圖9(a)可以發現,在初始條件(0.2, 0.2, 0.2, 0.2, 0.2)下,隨著耦合強度ρ2從0開始正向增大,系統一開始就進入混沌放電狀態,直到ρ2=-0.7,期間存在周期窗口ρ2=0.1 6,ρ2=-0.51,隨后通過反向倍周期分岔路徑轉為周期尖峰放電。李雅普諾夫指數譜表現的動力學狀態分布與分岔圖所展示的動力學基本一致。圖10給出了不同突觸耦合強度ρ2時,系統所產生的不同動力學現象,包括混沌、瞬態混沌、準周期以及周期行為。 圖9 關于憶阻突觸耦合強度ρ2動力學狀態分布 從人工智能應用的角度來看,神經網絡模型的電路實現具有重要的現實意義和必要性。通常,非線性動力學系統可以通過采用基本模擬電子電路實現。本節利用模擬運算放大器、模擬乘法器、電阻、電容對提出的局部有源憶阻突觸耦合HR神經元網絡進行電路設計與實現。基于圖3的憶阻器電路和耦合HR神經元網絡(9),局部有源憶阻突觸耦合HR神經元網絡電路如圖11所示。其中,系統狀態變量x1, y1, x2, y2, z通過5個電容積分器的輸出電壓表示。基于基爾霍夫電路定律,系統電路的等效電路方程為 圖10 不同憶阻突觸耦合強度ρ2所對應的多種動力學行為 圖11 局部有源憶阻突觸耦合HR神經元網絡電路 假設C=10 nF, 根據系統參數與電路元件,部分電路元件阻抗值為:R=1 0 k Ω, R1=R6=R=10 kΩ, R2= R7=Rg/b=3.33 kΩ, R3= R8=Rg2/a =10 kΩ, R4= R9=Rg/c=2 kΩ, R5=R10=10 kΩ,RL1= Rg2/ρ1,RL2= Rg2/ρ2。為了驗證數值仿真,在PSIM電路仿真軟件中創建圖12所示電路。仿真過程中,5個電容初始電壓設置為(0.2V, 0.2V, 0.2V, 0.2V, 0.2V)。當I1=-0.05 mA,I2=0.25 mA, Ic=0.1 mA, ρ2=0.1, 相應的阻抗RL2= 100 kΩ, 調節不同的RL1,可以得到多種放電模式,如圖13所示。當ρ1=-0.4,相應的阻抗RL1=25 kΩ,調節不同的RL2,可以得到不同的動力學行為,如圖14所示。顯然,在圖13與圖14的電路仿真結果很好地驗證了圖8與圖10的數值仿真結果。 圖12 憶阻耦合神經元網絡PSIM仿真電路 圖13 局部有源憶阻突觸耦合HR神經元網絡電路仿真結果 圖14 局部有源憶阻突觸耦合HR神經元網絡電路仿真結果 本文設計了一種簡單的局部有源憶阻器模型。通過理論分析、數值模擬以及電路實現,證明了該憶阻器的緊磁滯回線特征和局部有源屬性。此外,利用該局部有源憶阻模型模擬生物突觸特點,構建了一種局部有源憶阻突觸耦合HR神經元網絡。研究結果表明,該憶阻神經網絡在不同的突觸耦合強度下能表現出多種放電模式和混沌動力學行為,具有豐富的動力學特性。最后,通過采用模擬電子元件實現局部有源憶阻耦合HR神經元網絡電路,并在PSIM電路仿真軟件中得到新系統的多種放電行為和不同吸引子,從而證實了系統的有效性。
2.4 電路模型



3 局部有源憶阻突觸耦合HR神經網絡
3.1 模型建立
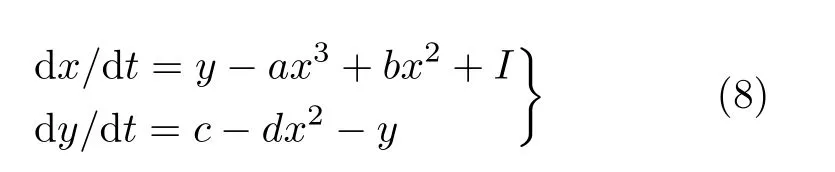


3.2 突觸耦合強度相關動力學


4 電路設計與PSIM仿真驗證



5 結束語

