數感發展水平測評工具的設計與分析

閆云梅?龍娟娟

【摘 要】數感是人的一種基本的數學素養，近年來受到數學教育工作者的廣泛重視。2001年“數感”一詞出現在《全日制義務教育數學課程標準（實驗稿）》中，時隔20年，我國學生數感發展水平的現狀如何？本文采用水平評價的方式，在分析數感內涵和數感主要行為表現的基礎上，確定了評價數感的主要內容和觀測點，開發設計了低年級學生數感發展水平測評工具。經檢驗各項指標均達到測量學的標準，是一份科學的試卷。通過對300名學生的測試，得出一些初步的結論。

【關鍵詞】測評工具 數感 小學低年級

一、問題的提出

《全日制義務教育數學課程標準（實驗稿）》中將“數感”作為核心概念之首，自此，“數感”成為我國數學教育工作者耳熟能詳的術語，有關培養學生數感的方法與策略也應運而生。時隔20年，我國學生數感發展水平的現狀又是怎樣呢？筆者在中國知網上輸入“數感培養的策略”，共檢索到510條結果，而輸入“數感發展現狀”，則只檢索到21條結果。從兩項數據的對比可以看出，雖然教育工作者注重了數感的培養，但有關數感的評價還沒有得到應有的重視。究其原因，一方面是由于數感雖然易于理解，但是很難界定;另一方面是我國對于數感水平的評估缺少明確的評價標準和相應的測評工具。因此，筆者試圖依據表現性評價的理論，開發設計評價學生數感發展水平的測評工具，以期更全面、客觀地了解學生數感發展水平的現狀。

二、小學生數感發展測評工具設計的理論依據

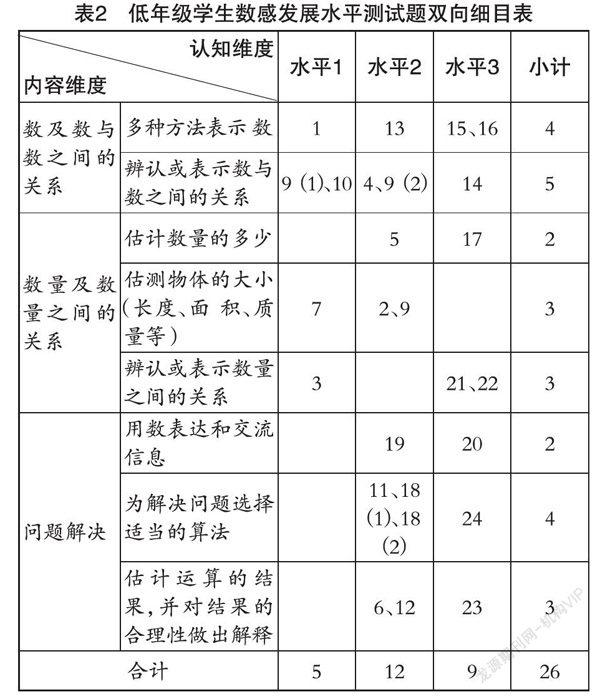
為了保證測評工具設計的科學性與普適性，我們以《義務教育數學課程標準（2011年版）》中對“數感”的表述為依據：數感主要是指關于數與數量、數量關系、運算結果估計等方面的感悟。筆者認為，這里的“感悟”包含三方面內容：數及數與數之間的關系、數量及數量之間的關系、問題解決（含運算結果估計等）。

史寧中教授在《基本概念與運算法則》一書中指出，數學的本質是：在認識數量的同時認識數量之間的關系，在認識數的同時認識數之間的關系。基于此，“數及數與數之間的關系”“數量及數量之間的關系”“問題解決”全面涵蓋了數感所涉及的內容，可作為數感測評內容維度的一級指標。

在此基礎上，只有將上述三方面的“感悟”轉化為具體的行為表現，才能進行數感的水平測評。那么，數感的主要表現是什么呢？

在《全日制義務教育數學課程標準（實驗稿）》中，對數感的主要表現給出了這樣的描述：理解數的意義;能用多種方法表示數;能在具體的情境中把握數的相對大小關系;能用數來表達和交流信息;能為解決問題而選擇適當的算法;能估計運算的結果，并對結果的合理性做出解釋。

綜合《全日制義務教育數學課程標準（實驗稿）》中數感的主要表現以及不同學者的觀點，筆者對數感測評內容維度框架進行了設計。（詳見表1）

三、小學生數感測評主要觀測點與雙向細目表

有了測評框架，我們又在每個二級指標下，進行了主要觀測點的設計，用以研制測評試題。

1. 多種方法表示（表征）數

（1）數的多模型表征——用小棒、計數器等不同的模型表示數;

（2）數的多模式表征——用不同的算式表示數，如50=25+25=10+10+10+10+10=60-10=70-20=100-50=10×5=2×25=…

2. 辨認或表示數與數之間的關系

（1）數與數之間相差關系的辨認;

（2）對數自身特征的認識，如平方數的辨認。

3.估計數量的多少

（1）自選標準，對整齊排列的物品數量的估計;

（2）給出標準，對無序排列的物品數量的估計。

4.估測物體的大小（包括長度、面積、質量等）

（1）根據給出的標準估測物體的長短;

（2）根據已有的經驗估測物體的質量或長短。

5.辨認或表示數量之間的關系

（1）發現并描述兩個（三個）數量間的相差關系;

（2）發現并描述數量間的倍數關系。

6.用數表達和交流信息

（1）根據現實生活情境提取數學信息進行交流;

（2）根據統計圖提取數學信息進行交流，并關注到數量之間的關系。

7.為解決問題選擇適當的算法

（1）在計算題中根據數的特征選擇合適的算法;

（2）在實際問題中根據數的特征和問題情境選擇合適的方法（估算、計算或推理）解決問題。

8.估計運算的結果，并對結果的合理性做出解釋

（1）估計算式的結果;

（2）用估算解決問題，并根據數的特征和情境做出解釋。

通過上述觀測點的確定，可以從不同角度了解學生數感發展的狀況，力求對學生做出全面客觀的評價。

在認知維度方面，本測評工具不是單純依賴正確或錯誤做出評判，而是根據學生作答情況，采用水平評價的方式，依據試題的難易度、開放度及學生試測過程中的表現，將試題分為水平1、水平2和水平3三個層次，水平3的難度最大。（詳見表2）

在題型設計方面，本測試設計選擇題、填空題、簡答題和解決問題共四個類型26道題目。其中簡答題和解決問題，根據學生的表達情況進行水平判定，大多設計為水平2或水平3的題目;填空題和選擇題，大多設計為水平1或水平2的題目。

四、小學生數感發展水平的評價

為了便于統計各項數據，測試采用先進行水平判定再賦值計分的方式。水平1的題目，根據學生作答情況分為水平A和水平B，分別計0分和1分;水平2的題目分為A，B，C三個水平，分別計0、1、2分，同理，水平3的題目根據學生作答情況分別計0、1、2、3分。

為了統一水平判定標準，每道試題都有明確的評價量規。先根據已有的經驗進行不同水平的劃分，再根據預測試中學生的作答情況進行調整，最終以描述加案例的方式形成每道題的評價量規，便于教師評價使用。

案例一：選擇題

8.我們把樹干一周的長度叫做“樹圍”，圖1中的大樹被7個成年人合抱，你估計這棵樹的樹圍大約是（）米。

A.30 ? ? ? ? ? ?B.10 ? ? ? ? ? ?C.7 ? ? ? ? D.4

此題測試目的是測試學生能否根據已有的經驗估測物體的長短，了解現實情境中數量的實際意義，為水平2的題目。

評價量規：

水平A：選A或D，說明學生對每個人1庹的長度缺乏清晰的認識。

水平B：選C，說明學生對每個人1庹的長度有一定認識，但不能依據經驗結合實際情況進行合理的估。

水平C：選B，說明學生對每個人1庹的長度有一定認識，并能依據經驗結合實際情況進行合理的估測。

案例二：解決問題

23.學校組織三、四年級學生看電影，三年級有426人，四年級有313人。

影院有700個座位，你覺得這些座位夠坐嗎？請你用自己喜歡的方式（畫圖、算式、文字表達等）說明你的理由。

此題測試目的是測試學生能否依據問題情境和數據的特點，對數據進行靈活處理，估計運算的結果并做出合理的解釋。

評價量規：

水平A：不作答或方法完全不正確。

水平B：沒有估算意識，對數據沒有處理，采用計算的方法做出正確的判斷。（如圖2）

水平C：有估算的意識和方法，對數據進行了處理并做出正確判斷，但方法不夠簡潔。（如圖3）

水平D：有估算的意識，能結合情境對數據進行處理，用簡潔的方法做出正確的判斷。（如圖4）

五、數感表現性評價測評工具的項目分析

本研究項目分析的主要內容包括難度、鑒別度、獨立樣本T檢驗、信度和效度分析，調研人員為區域內9所學校中隨機選擇的300名三年級學生（原二年級學生，因特殊原因，測試時間推遲到三年級開學）。

（一）難度和鑒別度指數

難度指的是本測量問卷的難易程度。一般而言，一份較佳的成績測驗應是大部分的試題的P值介于0.2至0.8之間。

鑒別度表示的是高分組答對的百分比與低分組答對百分比的差異值，主要目的是判別試題是否具有區別受試者能力高低的功能。一般認為，鑒別度指標值介于-1和1之間，當為負值時表示該題不具鑒別度，當為正值時且數值越大表示該題的鑒別度越高，最好在0.3以上。

結果顯示，本測試共26題，有21道題的難度在0.2至0.8之間，26道題的鑒別度指標值均為正值且其中19道題的鑒別度在0.3以上。可以看出，本測試題難易適中，試題的鑒別度較好。

（二）臨界比

項目分析的判別指標中，需要求出問卷個別題項的決斷值——CR值（又稱臨界比），最常用的是臨界比值法，此法又稱為極端值法。本研究測驗總分為56分，將測驗總分區分出高分組（≥41分）和低分組（≤31分），采取SPSS獨立樣本T檢驗，求出高、低兩組在每個題項的平均數差異的顯著性。在量表項目分析中，若采用極端值的臨界比，一般將臨界比值的t統計量的標準值設為3.000，若是題項高、低分組差異的t統計量小于3.0000，則表示題項的鑒別度較差。

依據決斷值的指標來判別，24道題的t值均大于3.0000，只有2道題的t值小于3.0000，說明此測試卷的鑒別度較好。

（三）信度

信度系數在項目分析中，可作為同質性檢驗的指標之一。信度代表量表的一致性或穩定性，一般采用克隆巴赫α系數。一般認為，0.50≤α系數<0.60，表示可以接受;0.60≤α系數<0.70，表示尚佳;0.70≤α系數<0.80，表示佳，信度高;0.80≤α系數<0.90，表示甚佳，信度很高;α系數≥0.90，表示非常好。

按照分量表信度指標值的判別準則，此次測試的“數及數與數之間的關系”“數量及數量之間的關系”“問題解決”三個維度的信度分別為0.614、0.604和0.615，屬于尚可，可以接受;總的測試卷信度為0.815，表示該測試卷整體信度很高。

（四）效度

所謂效度，指的是能夠測得該測驗所欲測心理或行為特質到何種程度。本研究效度主要采取建構效度，采用KMO統計量來判別題項間是否適合進行因素分析。一般認為，當KMO指標值大于0.80，表示題項變量間的關系是良好的，適合進行因素分析。

此次測試的KMO值等于0.822，表示題項變量間的關系是良好的;Bartlett球形檢驗的近似卡方分布為1252.652，自由度為325，顯著性概率值p=0.000<0.05，達到顯著性水平。

六、結論

1.本測試完成了低年級學生數感發展水平測評工具的設計與分析，在對整個測評工具的項目分析中得出，該工具的難度、鑒別度、獨立樣本T檢驗、信度和效度分析均達到測量學的標準，是一份科學的試卷。

2.通過水平評價的方式發現，不同學校學生數感發展水平在低年級已經呈現出顯著差異，這說明盡管數感有先天的成分，但學生數感的發展與學校教育有密切的關系，低年級是培養學生數感的關鍵期。

3.學生數感的發展水平與性別無關。

4.學生所有水平1試題滿分率的平均值為82.8%，水平2和水平3試題滿分率的平均值分別為55.3%和26.6%，說明該區域低年級學生數感發展尚處于中等水平，還有很大的成長空間。

5.學生在“數及數與數之間的關系”方面的滿分率明顯高于“數量及數量之間的關系”的滿分率，反映出“數量及數量關系”的學習沒有得到應有的重視。在“問題解決”方面的滿分率最低，說明學生在實際情境中應用數感靈活解決問題的能力有待提高。

【參考文獻】

[1]史寧中.基本概念與運算法則[M].北京：高等教育出版社，2013.

[2]吳明隆.問卷統計分析實務——SPSS操作與應用[M].重慶：重慶大學出版社，2014.

注：本文系北京市教育科學“十三五”規劃2017年度一般課題“基于數學素養，小學生‘數感發展的表現性評價與促進研究”（課題編號：CDEB17318）研究成果之一。