考慮輸出約束的機(jī)械臂命令濾波反步控制

林孟豪,張蕾,李鵬飛,王曉華,王文杰

(西安工程大學(xué)電子信息學(xué)院,710048,西安)

柔性關(guān)節(jié)機(jī)械臂具有高適應(yīng)性、低能耗、質(zhì)量輕等特點(diǎn),能夠代替人類(lèi)在航天、高精度制造工藝、醫(yī)療等領(lǐng)域進(jìn)行復(fù)雜、危險(xiǎn)的工作[1-2]。然而,隨著關(guān)節(jié)數(shù)量的增加,會(huì)導(dǎo)致柔性關(guān)節(jié)機(jī)械臂的響應(yīng)速度、軌跡跟蹤精度等問(wèn)題變得更加復(fù)雜。另外,由于單連桿柔性關(guān)節(jié)機(jī)械臂靈敏度低、應(yīng)用范圍受限,因此降低了單連桿柔性關(guān)節(jié)機(jī)械臂控制策略研究的應(yīng)用價(jià)值。因此,研究雙連桿柔性關(guān)節(jié)機(jī)械臂的軌跡跟蹤響應(yīng)速度、軌跡跟蹤控制精度等問(wèn)題具有重要的理論意義和應(yīng)用價(jià)值。

針對(duì)以上問(wèn)題,文獻(xiàn)[3]較早地設(shè)計(jì)出PD自適應(yīng)控制器,提高了柔性關(guān)節(jié)機(jī)械臂的軌跡跟蹤精度,但是并未考慮機(jī)械臂系統(tǒng)的穩(wěn)定性問(wèn)題。文獻(xiàn)[4]提出了混合控制策略,優(yōu)化控制器的設(shè)計(jì),并生成混合軌跡,雖然提高了柔性關(guān)節(jié)機(jī)械臂系統(tǒng)的魯棒性,但是沒(méi)有考慮機(jī)械臂的軌跡跟蹤精度。文獻(xiàn)[5]提出一種模糊優(yōu)化控制方法,設(shè)計(jì)出自適應(yīng)魯棒控制器,確保了柔性關(guān)節(jié)機(jī)械臂軌跡跟蹤精度,并提高了魯棒性,但是沒(méi)有考慮機(jī)械臂的軌跡跟蹤響應(yīng)速度問(wèn)題。文獻(xiàn)[6]針對(duì)機(jī)械臂參數(shù)不確定影響軌跡跟蹤性能的問(wèn)題,采用兩個(gè)RBF神經(jīng)網(wǎng)絡(luò)同時(shí)處理不確定參數(shù),顯著提高了軌跡跟蹤性能,但并未考慮擾動(dòng)誤差對(duì)機(jī)械臂系統(tǒng)的影響。文獻(xiàn)[7]通過(guò)設(shè)計(jì)一種基于奇異攝動(dòng)理論的有界控制器,采用模糊邏輯控制參數(shù)自動(dòng)調(diào)整,保證了柔性關(guān)節(jié)機(jī)械臂的軌跡跟蹤精度和響應(yīng)速度,但是卻增加了機(jī)械臂系統(tǒng)的計(jì)算復(fù)雜度。然而,上述研究?jī)?nèi)容均未考慮柔性關(guān)節(jié)機(jī)械臂系統(tǒng)的輸出約束與計(jì)算復(fù)雜等問(wèn)題對(duì)提高機(jī)械臂系統(tǒng)軌跡跟蹤響應(yīng)速度與軌跡跟蹤精度的影響。

為了保證機(jī)械臂系統(tǒng)的軌跡跟蹤精度,需要將系統(tǒng)的跟蹤誤差約束在預(yù)先設(shè)定的范圍內(nèi)。目前針對(duì)此類(lèi)研究的方法主要有模型預(yù)測(cè)控制[8],Funnel控制[9]和障礙李雅普諾夫函數(shù)(barrier Lyapunov function,BLF)[10]等。文獻(xiàn)[11]基于常對(duì)數(shù)型障礙李雅普諾夫函數(shù),提出全狀態(tài)反饋神經(jīng)網(wǎng)絡(luò)控制策略,保證了柔性關(guān)節(jié)機(jī)械臂的軌跡跟蹤精度,提高了系統(tǒng)的魯棒性,但并未考慮機(jī)械臂系統(tǒng)的軌跡跟蹤響應(yīng)速度問(wèn)題。文獻(xiàn)[12]基于時(shí)變正切型障礙李雅普諾夫函數(shù),提出了一種自適應(yīng)控制策略,解決了帶有輸出約束和模型不確定的柔性關(guān)節(jié)機(jī)械臂軌跡跟蹤響應(yīng)速度較慢的問(wèn)題。然而,障礙李雅普諾夫函數(shù)的應(yīng)用會(huì)造成系統(tǒng)的計(jì)算難度增大。文獻(xiàn)[13]針對(duì)柔性關(guān)節(jié)機(jī)械臂計(jì)算量大、計(jì)算困難等問(wèn)題,設(shè)計(jì)了命令濾波控制器,降低了計(jì)算難度,但是該方法并沒(méi)有考慮到命令濾波器帶來(lái)的濾波誤差對(duì)整個(gè)控制系統(tǒng)的影響。

鑒于上述分析,本文提出一種具有輸出約束和誤差補(bǔ)償?shù)碾p連桿柔性關(guān)節(jié)機(jī)械臂命令濾波反步控制(barrier Lyapunov function with command-filtered backstepping control,BLF-CFBC)策略。首先采用常對(duì)數(shù)型障礙李雅普諾夫函數(shù)設(shè)計(jì)虛擬控制函數(shù),約束機(jī)械臂系統(tǒng)的軌跡跟蹤誤差;接著采用命令濾波器得到濾波后的虛擬控制函數(shù)及其導(dǎo)數(shù),降低反步法中的計(jì)算維度,并引用濾波補(bǔ)償機(jī)制,減少濾波誤差對(duì)整體系統(tǒng)的影響;最后,通過(guò)仿真實(shí)驗(yàn),證明了本文所提控制策略能夠達(dá)到提高雙連桿柔性關(guān)節(jié)機(jī)械臂系統(tǒng)軌跡跟蹤響應(yīng)速度與軌跡跟蹤精度的控制目標(biāo)。本文主要?jiǎng)?chuàng)新點(diǎn)如下:

(1)利用常對(duì)數(shù)型障礙李雅普諾夫函數(shù)解決了雙連桿柔性關(guān)節(jié)機(jī)械臂系統(tǒng)的輸出約束問(wèn)題;

(2)在雙連桿柔性關(guān)節(jié)機(jī)械臂模型反步遞推控制律過(guò)程中,采用命令濾波器降低了計(jì)算復(fù)雜度;

(3)通過(guò)引入誤差補(bǔ)償機(jī)制減少了采用命令濾波器帶來(lái)的誤差,并證明了系統(tǒng)補(bǔ)償后的跟蹤誤差有界性。

1 系統(tǒng)描述與控制目標(biāo)

本文以雙連桿柔性關(guān)節(jié)機(jī)械臂模型作為被控對(duì)象,其結(jié)構(gòu)示意圖如圖1所示。

圖1 雙連桿柔性關(guān)節(jié)機(jī)械臂示意圖

根據(jù)文獻(xiàn)[14],建立雙連桿柔性關(guān)節(jié)機(jī)械臂系統(tǒng)的動(dòng)力學(xué)模型如下

(1)

(2)

假設(shè)1[15]矩陣M(qi)(i=1,2)∈Rn×n為正定對(duì)稱(chēng)矩陣。

假設(shè)2[15]期望軌跡qdi(i=1,2)及其導(dǎo)數(shù)連續(xù)且有界。

本文的控制目標(biāo)是設(shè)計(jì)一個(gè)具有輸出約束和誤差補(bǔ)償?shù)碾p連桿柔性關(guān)節(jié)機(jī)械臂命令濾波反步控制策略,在保證系統(tǒng)中所有信號(hào)有界的前提下,使得系統(tǒng)的輸出qi(i=1,2)可以跟蹤期望軌跡qdi(i=1,2),并且跟蹤誤差qi-qdi(i=1,2)可以收斂到原點(diǎn)附近的一個(gè)領(lǐng)域內(nèi)。

2 命令濾波及障礙李雅普諾夫函數(shù)

本文所采用的二階命令濾波器定義如下[16]

(3)

本文所采用障礙李雅普諾夫函數(shù)定義如下。

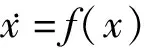
定義2[18]傳統(tǒng)對(duì)數(shù)型障礙李雅普諾夫函數(shù)表達(dá)式為

(4)

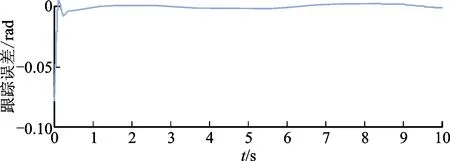
式中:ln(·)為自然對(duì)數(shù),i=1,2,3,4;vi為系統(tǒng)誤差變量;kbi>0為約束邊界,滿足|v(0)|

引理1[19]對(duì)任意常數(shù)kbi,若Z1={z1∈R:-kb1

(5)

式中:η=[ω,z1]T∈M,ω∈Rl,t∈R+,h為在定義域中關(guān)于t分段連續(xù)且滿足局部Lipschitz條件。假設(shè)存在函數(shù)U:Rl→R+和V1:Rl→R+在各自定義域上連續(xù)可微且正定,那么:

V1(z1)→∞,z1→-kb1或z1→Kb1

(6)

γ1(‖ω‖)≤U(‖ω‖)≤γ2(‖ω‖)

(7)

式中,γ1(·)、γ2(·)為K∞函數(shù)。取V(η)=V1(z,t)+U(ω),z1(0)∈Z1,則

(8)

成立,故z1(t)有界,z1∈(-kb1,kb1),?t∈[0,+∞),系統(tǒng)的解η(t)一致最終有界,并且當(dāng)t→∞時(shí),zi(t)→0,(i=1,2,…,n)。

3 控制器設(shè)計(jì)

在本節(jié)中,針對(duì)式(1)雙連桿柔性關(guān)節(jié)機(jī)械臂模型,設(shè)計(jì)具有輸出約束和誤差補(bǔ)償?shù)拿顬V波反步控制(BLF-CFBC)策略,使得雙連桿柔性關(guān)節(jié)機(jī)械臂的輸出軌跡能夠精準(zhǔn)跟蹤期望軌跡。

控制器具體設(shè)計(jì)思路如下:

(1)對(duì)雙連桿柔性關(guān)節(jié)機(jī)械臂動(dòng)力學(xué)模型式(1),選取系統(tǒng)的狀態(tài)變量并轉(zhuǎn)換為四階系統(tǒng)模型式(2),再采用反步法對(duì)系統(tǒng)模型進(jìn)行降階,選取狀態(tài)變量作為虛擬控制輸入,設(shè)計(jì)系統(tǒng)誤差變量;

(2)在思路(1)的基礎(chǔ)上對(duì)前兩階子系統(tǒng)引入障礙李雅普諾夫函數(shù),解決系統(tǒng)輸出約束問(wèn)題;

(3)在思路(2)的基礎(chǔ)上通過(guò)采用命令濾波器得到虛擬控制函數(shù)及其導(dǎo)數(shù),降低系統(tǒng)控制器的設(shè)計(jì)復(fù)雜度并引入誤差補(bǔ)償機(jī)制降低濾波誤差對(duì)系統(tǒng)的影響。

定義系統(tǒng)誤差變量為:z1i=x1i-x1di(i=1,2),z2i=x2i-α1i,c(i=1,2),z3i=x3i-α2i,c(i=1,2),z4i=x4i-α3i,c(i=1,2),其中x1di=gdi(i=1,2),αxi(x=1,2,3;i=1,2)為虛擬控制函數(shù),αxi,c(x=1,2,3;i=1,2)為經(jīng)過(guò)命令濾波器后的虛擬控制函數(shù)。由于命令濾波器的使用會(huì)產(chǎn)生濾波誤差,從而影響系統(tǒng)的整體性能。本文通過(guò)引入誤差補(bǔ)償變量來(lái)控制濾波誤差對(duì)系統(tǒng)的整體影響。

由文獻(xiàn)[21]可知,定義補(bǔ)償后的誤差變量為

v1i=z1i-ζ1i(i=1,2),v2i=z2i-ζ2i(i=1,2)

v3i=z3i-ζ3i(i=1,2),v4i=z1i-ζ4i(i=1,2)

本文采用反步法逆推地設(shè)計(jì)控制器,設(shè)計(jì)過(guò)程分為以下4個(gè)步驟。

第1步選取補(bǔ)償后的誤差變量為

v1i=z1i-ζ1i

(9)

對(duì)式(9)求導(dǎo)

(10)

根據(jù)定義1和定義2,構(gòu)造障礙李雅普諾夫函數(shù)為

(11)

對(duì)式(11)求導(dǎo),得

(12)

設(shè)計(jì)虛擬控制函數(shù)α1i(i=1,2)和誤差補(bǔ)償變量ζ1i(i=1,2)的導(dǎo)數(shù)為

(13)

(14)

式中:k1∈Rn×n為正定對(duì)稱(chēng)常數(shù)矩陣。

將式(13)(14)代入式(12),可得

(15)

第2步選取補(bǔ)償后的誤差變量

v2i=z2i-ζ2i

(16)

對(duì)式(16)求導(dǎo)

(17)

構(gòu)造李雅普諾夫函數(shù)為

(18)

對(duì)式(18)求導(dǎo),得

(19)

設(shè)計(jì)虛擬控制函數(shù)α2i(i=1,2)和誤差補(bǔ)償變量ζ2i(i=1,2)的導(dǎo)數(shù)為

(20)

(21)

式中k2∈Rn×n為正定對(duì)稱(chēng)常數(shù)矩陣。

通過(guò)引理3,將式(20)(21)代入(19),可得

(22)

第3步選取補(bǔ)償后的誤差變量為

v3i=z3i-ζ3i

(23)

對(duì)式(23)求導(dǎo),得

(24)

構(gòu)造李雅普諾夫函數(shù)為

(25)

對(duì)式(25)求導(dǎo),得

(26)

設(shè)計(jì)虛擬控制函數(shù)α3i(i=1,2)和誤差補(bǔ)償變量ζ3i(i=1,2)的導(dǎo)數(shù)為

(27)

(28)

式中,k3∈Rn×n為正定對(duì)稱(chēng)常數(shù)矩陣。

將式(27)(28)代入(26)可得

(29)

第4步選取補(bǔ)償后的誤差變量為

v4i=z4i-ζ4i

(30)

對(duì)式(30)求導(dǎo),得

(31)

構(gòu)造李雅普諾夫函數(shù)為

(32)

對(duì)式(32)求導(dǎo),得

(33)

在這一步中出現(xiàn)了系統(tǒng)的真實(shí)控制函數(shù),設(shè)計(jì)控制律τ為

(34)

根據(jù)文獻(xiàn)[21]設(shè)計(jì)系統(tǒng)的誤差補(bǔ)償變量ζ4i(i=1,2)的導(dǎo)數(shù)為

(35)

式中,k4∈Rn×n為正定對(duì)稱(chēng)常數(shù)矩陣。

將式(34)(35)代入(33),可得

(36)

4 穩(wěn)定性證明

(37)

式中,a為任意常數(shù)。

選取整個(gè)系統(tǒng)的李雅普諾夫函數(shù)為

(38)

對(duì)式(38)求導(dǎo),得

(39)

通過(guò)引理2,將虛擬控制律(13)(20)(27)和控制律(34)代入式(39),得

(40)

(41)

由引理4可知,式(41)的解為

Vs(t)≤e-φ(t-t0)V(t0)

(42)

由式(42)可得,Vs指數(shù)收斂至零,收斂速度取決于φ,并且當(dāng)t→∞時(shí),z1i→0(i=1,2),z2i→0(i=1,2),z3i→0(i=1,2),z4i→0(i=1,2)。

由補(bǔ)償后的誤差變量定義可知

vxi=zxi-ζxi(x=1,2,3,4;i=1,2)

(43)

(44)

根據(jù)k0的定義以及引理1可知,通過(guò)調(diào)節(jié)命令濾波參數(shù)與設(shè)計(jì)參數(shù)ki(i=1,2,3,4)可以保證系統(tǒng)補(bǔ)償后的跟蹤誤差v1i(i=1,2)有界,且能夠收斂到原點(diǎn)附近的一個(gè)領(lǐng)域內(nèi)。

由控制律表達(dá)式(34)可知系統(tǒng)控制器輸出有界,根據(jù)假設(shè)1與假設(shè)2,通過(guò)調(diào)用引理1,可證得補(bǔ)償后的機(jī)械臂系統(tǒng)所有閉環(huán)信號(hào)可保證一致最終有界。由于Vs(t)有界,?t≥0,根據(jù)定義1與定義2可得V1(z1i)→∞(i=1,2),|z1i|→kb1(i=1,2),|z1i|≠kb1,即輸出約束得到滿足。

5 仿真驗(yàn)證

為了驗(yàn)證本文所提BLF-CFBC控制策略的有效性,對(duì)圖1所示的雙連桿柔性關(guān)節(jié)機(jī)械臂模型進(jìn)行數(shù)值仿真。并將仿真結(jié)果與不具有輸出約束和誤差補(bǔ)償?shù)碾p連桿柔性關(guān)節(jié)機(jī)械臂命令濾波反步控制策略(CFBC)的結(jié)果進(jìn)行對(duì)比,其中CFBC與BLF-CFBC策略的參數(shù)設(shè)計(jì)如下

(45)

(46)

(47)

(48)

式中

(49)

(50)

(51)

其中q1、q2為機(jī)械臂關(guān)節(jié)的旋轉(zhuǎn)角度,g為重力加速度。

圖2 關(guān)節(jié)1軌跡跟蹤響應(yīng)曲線

圖2為CFBC策略與BLF-CFBC策略下,雙連桿柔性關(guān)節(jié)機(jī)械臂關(guān)節(jié)1的軌跡跟蹤響應(yīng)曲線圖。其中,CFBC策略下關(guān)節(jié)1在0.1 s后能夠跟蹤上期望軌跡曲線,而B(niǎo)LF-CFBC策略在0.08 s就能夠跟蹤上期望軌跡曲線,軌跡跟蹤響應(yīng)速度提升20%。

圖3表示CFBC策略與BLF-CFBC策略下,雙連桿柔性關(guān)節(jié)機(jī)械臂關(guān)節(jié)2的軌跡跟蹤響應(yīng)曲線圖,從圖中可以看出,CFBC策略下關(guān)節(jié)2在0.2 s后才能跟蹤上期望軌跡曲線,本研究所提BLF-CFBC策略下,關(guān)節(jié)2在0.14 s后能夠跟蹤上期望軌跡曲線,其軌跡跟蹤響應(yīng)速度提升了30%。

圖3 關(guān)節(jié)2軌跡跟蹤響應(yīng)曲線

圖4表示CFBC策略下,雙連桿柔性關(guān)節(jié)機(jī)械臂關(guān)節(jié)1與關(guān)節(jié)2的軌跡跟蹤誤差曲線圖,圖5表示BLF-CFBC策略下,雙連桿柔性關(guān)節(jié)機(jī)械臂關(guān)節(jié)1與關(guān)節(jié)2的軌跡跟蹤誤差曲線圖。

(a)關(guān)節(jié)1

(b)關(guān)節(jié)2

由圖4、5可知,對(duì)于雙連桿柔性關(guān)節(jié)機(jī)械臂系統(tǒng),CFBC策略的軌跡跟蹤誤差較大,而本文所提BLF-CFBC策略的軌跡跟蹤誤差明顯減小。由于障礙李雅普諾夫函數(shù)的應(yīng)用,可將軌跡跟蹤誤差約束在-kb與kb之間,kb>0為約束邊界,并且在誤差波形穩(wěn)定后,相比于CFBC策略,在BLF-CFBC策略下關(guān)節(jié)1的軌跡跟蹤誤差減少4%,關(guān)節(jié)2的軌跡跟蹤誤差減小3.5%,表明所提控制策略有效地提高了機(jī)械臂系統(tǒng)的軌跡跟蹤精度。

圖6為CFBC策略下雙連桿柔性關(guān)節(jié)機(jī)械臂關(guān)節(jié)1與關(guān)節(jié)2的控制力矩曲線圖。

(a)關(guān)節(jié)1

圖7為本文所提BLF-CFBC策略下關(guān)節(jié)1與關(guān)節(jié)2的控制力矩曲線圖。綜合圖6和圖7可見(jiàn),本文所提BLF-CFBC策略,控制力矩曲線峰值較小,意味著對(duì)機(jī)械臂中的電機(jī)損耗較小,而CFBC策略下控制力矩曲線峰值較大,可能會(huì)對(duì)機(jī)械臂中的電機(jī)造成強(qiáng)烈沖擊。

(a)關(guān)節(jié)1

綜合以上仿真結(jié)果可以得出:本文所提BLF-CFBC策略與CFBC策略相比較,雙連桿柔性關(guān)節(jié)機(jī)械臂的軌跡跟蹤響應(yīng)速度與軌跡跟蹤精度有明顯的提高,能夠達(dá)到較好的控制目標(biāo)。

6 結(jié) 論

本文以提高柔性關(guān)節(jié)機(jī)械臂軌跡跟蹤響應(yīng)速度和控制精度為目標(biāo),提出一種在常規(guī)反步控制算法中結(jié)合對(duì)數(shù)型障礙李雅普諾夫函數(shù)和命令濾波器算法的控制策略。通過(guò)構(gòu)造障礙李雅普諾夫函數(shù)加快軌跡跟蹤速度,同時(shí)將軌跡跟蹤誤差約束在設(shè)定的誤差范圍內(nèi);通過(guò)引入命令濾波器避免了常規(guī)反步法在高階系統(tǒng)設(shè)計(jì)時(shí)對(duì)控制變量反復(fù)求導(dǎo)導(dǎo)致的計(jì)算爆炸的問(wèn)題;設(shè)計(jì)命令濾波器誤差補(bǔ)償機(jī)制以削弱采用濾波器產(chǎn)生的誤差對(duì)跟蹤精度的影響。理論證明驗(yàn)證了本文所設(shè)計(jì)的控制策略可以保證軌跡跟蹤誤差的有界約束和所有閉環(huán)系統(tǒng)中的信號(hào)的一致最終有界。仿真結(jié)果表明,本文所提策略相比于不具有輸出約束和誤差補(bǔ)償?shù)拿顬V波反步控制策略,其控制精度和跟蹤誤差收斂時(shí)間都有提高。

未來(lái)的工作將會(huì)考慮在狀態(tài)變量部分未知的情況下,引入觀測(cè)器設(shè)計(jì)等控制算法[24-25],從而克服本文所提策略中所有狀態(tài)變量必須全部已知的約束條件。