時變信道中聯合信道估計的單載波迭代均衡接收機

蘭林瑤,穆鵬程

(西安交通大學電子與信息學部,710049,西安)

目前,將迭代思想和均衡技術相結合的單載波迭代均衡技術越來越多地應用于寬帶無線通信系統中。單載波通信作為一種寬帶無線通信技術,具有較低的峰均比及對頻偏和相位不敏感等優點,因此得到了廣泛的研究[1]。迭代均衡技術,作為一種聯合均衡和信道解碼的接收方法,能夠有效對抗符號間干擾,提供迭代增益,達到最優的系統整體性能。

文獻[2-4]介紹了基于最小均方誤差(MMSE)、判決反饋均衡(DFE)的單載波迭代均衡接收機,均衡模塊根據譯碼模塊反饋的軟信息進行線性、非線性均衡,經過多次迭代后獲得較優的系統性能。文獻[4]提出了一種基于時域反饋濾波器組的單載波迭代均衡器,該均衡器實現了多徑信號的最佳分離和分集合并效果,能夠應對多徑信道長度超過循環前綴長度的超大時延擴展,在消除誤比特率的“平臺效應”后獲得更好的系統性能。以上方法在準靜態信道下能取得較好的性能,但是在寬帶無線通信環境中,由于多徑效應及通信雙方的相對運動,信道往往呈現頻率選擇性和時間選擇性的雙重特征[5],因此研究快時變衰落信道下的迭代均衡技術具有較高的應用價值。

相比于準靜態信道,時變信道下的時頻域信道矩陣更為復雜,均衡計算復雜度大,為了降低計算復雜度,文獻[6-8]利用信道矩陣的準帶狀結構,根據反饋的對數似然比分別進行時頻域線性MMSE迭代軟均衡。文獻[9]提出了時變信道下基于MMSE的Turbo均衡結構,均衡模塊與譯碼模塊不斷進行軟信息的迭代交換,每次迭代的均衡信號經過解調、解交織、MAP譯碼輸出。然而,文獻[6-9]都假設時變信道已知,但是實際工程中信道往往是未知的,信道估計的精確性會直接影響到系統性能。

文獻[10-11]提出了基于導頻插值的信道估計方法,通過在發送數據中插入已知的導頻信息進行信道估計,首先估計出導頻處的信道特性,然后通過插值算法獲得數據處的信道估計。文獻[12]將基于導頻插值的信道估計和單載波迭代均衡技術聯合分析,在每次迭代中更新信道估計,提高信道估計精度,獲得迭代增益。然而,以上方法將傳輸數據流進行分塊處理,假設信道系數在每個數據塊上準靜態,在信道快速變化的場景下,估計性能下降。

在高速移動場景下,高速移動信道中的每一條可分徑在一個塊傳輸時間內是變化的,不再保持恒定,進而導致信道待估計參數的數量是準靜態過程的成百上千倍(取決于塊傳輸時間內抽樣點的個數),遠遠超過接收數據量的估計負荷。為了降低計算復雜度,同時精確地估計出動態信道狀態,基于基擴展模型(BEM)的信道估計算法得到了廣泛的應用。Tsatsanis最早提出采用復指數基擴展模型(complex exponential basis expansion model, CE-BEM)擬合時變信道[13],其原理是利用有限個基函數的線性組合來擬合快時變信道的時域響應。文獻[13-16]分析討論了采用基擴展模型的信道估計,通過BEM建模將對信道參數的估計轉變為對基函數的系數的估計,降低快時變信道中待估計參數的數量。文獻[17]提出了聯合基于BEM的信道估計和單載波迭代均衡的方法,通過插入導頻對基函數系數進行估計,在迭代過程中根據反饋信息和導頻信號不斷更新基函數系數,提高信道估計準確性,提升系統性能。

為了能有效地對抗時變信道下的大時延擴展,本文將文獻[4]中提出基于時域反饋濾波器組的單載波迭代均衡接收機擴展到時變信道,考慮到信道時變性,該均衡器的濾波器系數同樣具有時變性,因此能有效對抗時間選擇性衰落,實現時變信道下多徑信號的分集利用。考慮到實際工程中信道往往未知,我們采用基于BEM的信道估計方法對信道進行迭代估計。仿真分析表明,本文提出的迭代均衡接收機能夠有效對抗頻率選擇性衰落和時間選擇性衰落,獲得較優的系統性能。

1 系統模型

1.1 發射機模型

發射端信號處理過程如圖1所示。發送端發送一串信息比特數據流d(q),q=0,1…,Q-1,經過信道編碼、交織、P-QAM調制后得到符號序列a(k)∈χ,k=0,1…,K-1,其中χ={α0,α1,…,αP-1}為星座符號點集合。在設計幀結構中,往往會插入循環前綴(CP)或者獨特字(UW),一方面是為了充當保護間隔,另一方面是使線性卷積等效于循環卷積[18]。考慮到UW是已知的序列,為了充分利用這部分數據,本文采用UW充當導頻的幀結構,如圖2所示,通常要求UW的長度遠大于信道的最大時延。在圖中,對符號序列a(k)進行分塊處理,每塊符號末尾添加長度為Np的UW符號,構成大小為N的數據塊,同時將第一個數據塊設計為已知的導頻塊。

1.2 接收機結構

(1)

以一幀信號為周期,設每幀發射序列長度為K,則每幀接收信號表示為

x=Sh+v

(2)

式中:S=diag[s0,s1,…,sK-1]∈CK×KL表示信號矩陣,其中diag[]表示對角陣;sk=[s(k),s(k-1),…,s(k-L+1)]T,0≤k≤K-1表示由k時刻及k時刻以前的L-1個發射信號組成的向量,如果k時刻以前沒有信號,則補0;h=[h0,h1,…,hK-1]T表示信道系數向量,其中hk=[hk(0),hk(1),…,hk(L-1)]T,0≤k≤K-1存儲了第k時刻的所有的信道抽頭響應,長度為L;v表示均值為0、方差為σ2的加性復高斯白噪聲向量。

為了提高接收機性能,充分利用多徑時延帶來的信號分集,克服頻率選擇性衰落和時間選擇性衰落,本文設計了一種如圖3所示的聯合信道估計的單載波迭代均衡接收機。在文獻[4]中,分析和討論了信號在時不變信道中的迭代均衡結構,考慮到實際無線通信中信道脈沖響應未知且時變,本文將文獻[4]中的結構擴展到時變信道場景,同時加入信道估計模塊,對信道響應進行迭代估計。

圖3 聯合信道估計的單載波迭代均衡結構

2 濾波器系數優化

考慮到信道的時變性,反饋濾波器組系數和前饋濾波器組系數同樣具有時變性。參考文獻[4]中的系數優化方法,得到第n時刻第m組反饋濾波器組最優系數解

(3)

式中:l=0,1,…,L-1,0≤m≤M-1;根據文獻[4]

可得

(4)

第n時刻前饋濾波器最優系數解為

(5)

(6)

(7)

3 信道迭代估計

3.1 CE-BEM時變信道建模

由于時變信道的未知參數常大于能提供的訓練序列或導頻符號的個數,無法直接估計信道,因此采用建立模型的方法對信道進行逼近,這樣可以減少待估計的參數個數。基擴展思想最早由M.K.Tsatsanis以復指數BEM(CE-BEM)為基函數提出來用于時變信道建模的,由于CE-BEM實現簡單,得到了廣泛地應用。但同時,該算法也存在較大的建模誤差,這是因為多普勒譜多為浴盆形、鐘形或者二者的結合形狀,而CE-BEM是基于白譜的。本文將CE-BEM估計算法與迭代思想聯合起來,通過每次估計不斷更新信道信息,能夠有效提高系統性能,改善CE-BEM誤差。

利用CE-BEM模型建模,時變抽頭系數可以表示為

(8)

式中:cq(l)表示在第l條徑的第q個BEM系數,是均值為0、方差為σl的復高斯隨機變量[5];bq(n)表示第q個基函數,表達式為

bq(n)=ejωqk,k=0,1,…,K-1

(9)

為了便于分析,將時變信道系數用向量形式表示為

h=(U?IL)c

(10)

式中:?表示克羅內克積;U=[u0,u1,…,uQ]∈CK×(Q+1)表示基函數矩陣,其中uq=[ejωq0,ejωq1,…,ejωqK]T,0≤q≤Q;c=[c0(l),c1(l),…,cQ(l)]T表示BEM系數向量,其中cq(l)=[cq(0),cq(1),…,cq(L-1)]T。

同樣,將時變信道用矩陣形式表示為

(11)

式中:Cq是由[cq(l),0N-L]T為第一列元素構成的循環矩陣;H是維度為K×K的時變信道矩陣。

3.2 基于CE-BEM模型的信道迭代估計

在迭代次數i=0時,考慮到發射數據信號不已知,提取每一幀接收信號的導頻部分,用矩陣來表示,同式(2)中信號矩陣S的表示方式,其中導頻信號矩陣:Sp∈CNp×NpL,其中Np表示一幀信號中導頻長度。相應地,導頻信號對應的BEM函數矩陣表示為Up。則接收端的導頻位置上的信號向量為

xp=Sp(Up?IL)c+v=Apc+v

(12)

應用最小二乘估計[14,17],得到BEM系數估計

(13)

考慮到應用頻域均衡需要進行分塊處理,將U表示成分塊矩陣形式,即U=[U1,…,UJ]T,其中第j塊BEM函數矩陣表示為Uj=[u0,j,u1,j,…,uQ,j]∈CN×(Q+1)。第j塊數據的時域信道矩陣表示為

(14)

應用頻域MMSE均衡,有

(15)

轉換到時域并進行歸一化,歸一化系數為

(16)

所以第j塊均衡信號可以表示為

(17)

當迭代次數i>0,采用時域迭代均衡結構進行處理,將上一次迭代譯碼輸出的軟信息進行交織、調制得到反饋信號,反饋信號與導頻信號構成發射信號估計,利用最小二乘法估計BEM系數,更新信道信息。

第i次迭代中接收端信號向量可以表達為

x=S(i)(U?IL)c+v=A(i)c+v

(18)

其中S(i)是導頻信號和上一次迭代得到的反饋信號組成信號矩陣,與信號矩陣S的表示方式相同。

應用最小二乘估計,得到BEM系數估計

(19)

則第i次迭代中每一幀信號的時域信道系數向量估計為

(20)

4 仿真分析

為了比較本文所提出的聯合信道估計的單載波迭代均衡方法性能,我們通過數值仿真將其與文獻[14]中提出的聯合最小二乘信道估計的頻域迭代均衡方法進行對比。文獻[14]中提出了一種在快時變信道下適用于正交頻分復用(OFDM)調制的迭代均衡的方法,同時也適用于單載波調制系統。考慮到一般的應用場景中大時延擴展和大多普勒頻偏往往不會同時出現,這種情況經常出現在水聲通信等特定的通信環境中[19],所以我們分別比較分析了大時延擴展、較小多普勒頻偏和大多普勒頻偏、較小時延擴展兩種情形下的誤比特率(BER)和誤幀率(FER)。

本文采用Jakes信道模型[20]來近似時變信道,生成瑞利衰落信道,任意時刻每一條路徑功率相等,對信道增益歸一化,有E(hn,l)=1/L,符號采樣周期Ts=50 ns。其余仿真參數設置如下:幀內DFT塊數為10,FFT點數為256。信道編碼方式采用1/2卷積碼[171,133],譯碼方式采用MAP譯碼器,交織方式采用幀內比特隨機交織,采用Gray映射,調制方式為QPSK。

為簡化表達,令CEiter-*代表本文所提出的聯合信道估計的迭代均衡方法,其中*表示迭代次數,iter-*表示本文所提出的方法在信道已知下的情況,LSiter-*表示文獻[14]中的所提出的聯合最小二乘信道估計的頻域迭代均衡方法,MFB(Matched Filter Bound)表示匹配濾波界[21],是理論上的性能最優界。圖4和圖5是大時延擴展較小多普勒頻偏情形下得到的BER和FER。在這種情況下,最大時延設置為τmax=1.55 μs,即信道長度L=32,信號分量數設置為M=32,最大多普勒頻偏設置為fmax=100 Hz,UW長度設置為Np=64。從圖中可以看出,在信道大時延擴展而多普勒頻偏較小的情況下,迭代3次后,本文所提出的方法相比于對比方法,當BER為10-5時,BER性能改善1 dB,距離MFB大約1 dB;當FER為10-3時,FER性能改善大約1.5 dB,距離MFB大約0.8 dB。在信道已知的情況下,本文所提出的方法的BER和FER性能均接近MFB。

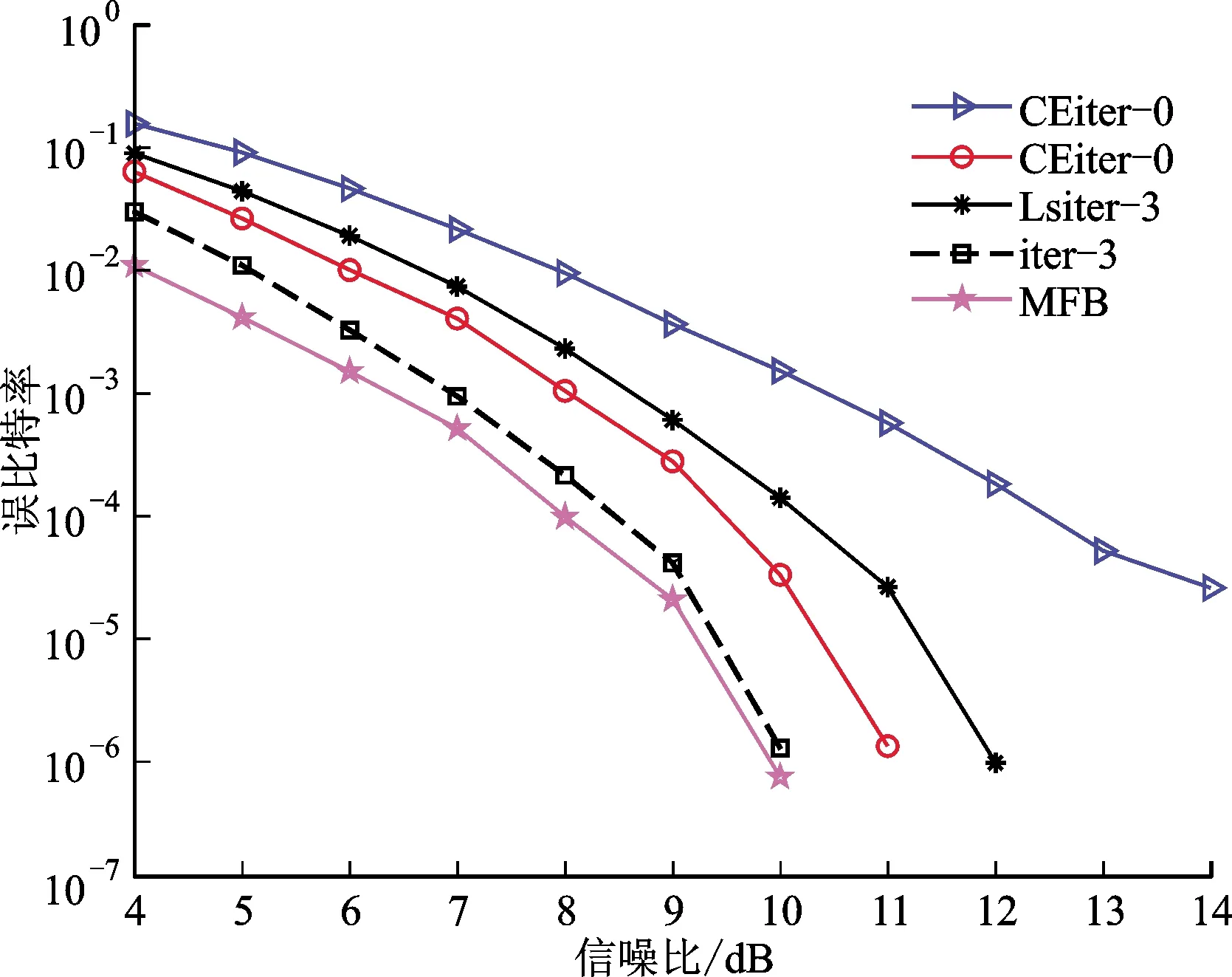
圖4 τmax=1.55 μs、fmax=100 Hz下的誤比特率

圖5 τmax=1.55 μs、fmax=100 Hz下的誤幀率

圖6和圖7是大多普勒頻偏較小時延擴展情形下得到的BER和FER。在這種情況下最大時延設置為τmax=0.5 μs,即信道長度L=11,信號分量數設置為M=11,最大多普勒頻偏設置為fmax=926 Hz,UW長度設置為Np=32。從圖中可以看出,在多普勒頻偏較大,時延擴展較小的情況下,迭代3次后,本文所提出的方法相比于對比方法,當BER為10-5時,BER性能改善大約2 dB,距離MFB大約0.8 dB;當FER為10-3時,FER性能改善大約3 dB,距離MFB大約0.3 dB。在信道已知的情況下,本文所提出的方法的BER和FER性能均接近MFB。

圖6 τmax=0.5 μs、fmax=926 Hz下的誤比特率

圖7 τmax=0.5 μs、fmax=926 Hz下的誤幀率

為進一步說明本文所提出的方法分別在大時延擴展較小多普勒頻偏和大多普勒頻偏較小時延擴展情形下信道估計的性能差異,圖8提供了本文方法不同參數設置下信道估計的均方誤差(MSE)性能,其中MSE的計算公式參考文獻[12]。

圖8 本文方法在不同參數設置下信道估計MSE性能比較

從圖8中可以發現,在較小時延擴展較大多普勒頻偏下,信道估計更為準確。結合圖4和圖6的仿真結果,可以發現在達到相同的誤比特的情況下,較小時延擴展較大多普勒頻偏情形下靈敏度更高。這是因為在本文中設置UW充當循環前綴和導頻,在較大時延擴展的參數設置下,UW長度為信道長度的2倍,而在較小時延擴展情形的參數設置下,UW長度為信道長度的3倍,可用導頻相比于信道長度所占的比例更大,對于信道的估計更為準確。

5 結 論

本文提出了一種在快時變信道下聯合信道估計的單載波迭代均衡接收機,利用多徑時延的分集性,設計了反饋濾波器組和前饋濾波器,用于消除不同時延符號下的干擾并實現分集合并。考慮到在實際工程中,信道往往未知,因此設計了信道迭代估計方法。通過設計基于UW的導頻幀結構,利用基于CE-BEM模型的信道估計方法,對信道進行迭代估計,提升信道估計精度,獲得較優系統性能。仿真結果表明,本文所提出的方法聯合信道估計和迭代均衡,能實現對時變信道較為準確的估計,有效消除符號干擾,同時在大時延擴展而多普勒頻偏較小和多普勒頻偏較大而時延擴展較小的兩種情況下獲得較優的系統性能,經過多次迭代后性能接近匹配濾波界。本文方法還可以擴展到多天線系統[22-25],進一步提升空時、空頻均衡系統的性能。