基于地球系統模式的局地化粒子濾波器與集合卡爾曼濾波器同化實驗

張鈺婷，沈浙奇,2,3*，伍艷玲,2,3

(1.自然資源部第二海洋研究所 衛星海洋環境動力學國家重點實驗室，浙江 杭州 310012；2.河海大學 海洋學院 資料同化與預測研究所，江蘇 南京 210098；3.南方海洋科學與工程廣東省實驗室（珠海），珠海 廣東 519080)

1 引言

作為研究大氣、海洋科學熱門課題之一，資料同化技術不僅可以為海洋數值預報模式提供初始場，還可以構造海洋再分析資料集，為海洋觀測計劃和數值預報模式物理量及參數等提供設計依據，近年來得到了廣泛的研究和應用[1]。集合卡爾曼濾波器（EnKF）是一種有效的資料同化方法，自Evensen[2]于1994年首次提出以來經過了20多年的發展和改進，已經在海洋資料同化中得到了廣泛的研究和應用。近年來，隨著動力模式的不斷發展和計算能力的提高，粒子濾波器（PF）由于不受模型線性和誤差高斯分布假設的約束，也逐漸成為了當前資料同化算法研究的熱門[3]。

EnKF是集合預報同卡爾曼濾波器（KF）的結合，它使用集合表示模式變量的概率密度分布，并采用KF的更新公式提供線性模型高斯分布假設下的同化最優解。由于EnKF避免了卡爾曼濾波器和擴展卡爾曼濾波器（EKF）中的協方差更新模型，使得它能夠被應用于大型地球物理模式。集合調整卡爾曼濾波器（EAKF）是在EnKF基礎上發展起來的衍生方法，它一般被視為一種確定性的EnKF格式[4]。EAKF從濾波理論出發推導了一個用于模式變量更新的算子，取代了傳統EnKF中的增益矩陣，且無需增加額外的觀測擾動，在計算量上有一定的優勢[4–5]。作為目前海洋資料同化所采用的主流方法之一—集合卡爾曼濾波器以及衍生方法隱含了預報集合高斯分布的假設，適用于線性系統的同化[6]。

相較于集合卡爾曼濾波，粒子濾波不含高斯假設，對非線性非高斯同化系統能產生更好的同化效果。粒子濾波算法基于貝葉斯估計理論，是貝葉斯公式的蒙特卡羅算法近似。“粒子”與集合卡爾曼濾波器中的集合成員相同，是用于表示模式變量的概率分布的集合樣本。如果計算資源充足，隨著粒子數目的增加，粒子的概率密度分布會逐漸趨向于真實狀態場的概率密度分布，粒子濾波器能夠實現最優貝葉斯估計的同化效果[3,7]。經典的粒子濾波器使用似然函數計算每個粒子的標量權重，因此當狀態場空間的維數較大時，狀態場數值的微小變化會引起對應權重在量級上的巨大變化，多數集合成員會因權重過小而失效，從而導致粒子濾波器的退化[8]。相當多的方法已經被提出來處理粒子濾波器中的退化[9]，如最優重要性粒子濾波器[10]、等權重粒子濾波器[11]、集合卡爾曼粒子濾波器[12]、局地化粒子濾波器[8,13]等。本文主要考察的局地化粒子濾波器是最近才被提出的一種同化方法，它通過在經典粒子濾波器中引入EnKF中常用的局地化方法來解決粒子濾波器的退化問題，得到了廣泛關注。

局地化方法自21世紀初在集合卡爾曼濾波器的同化中被提出以來[14]，已經被廣泛地應用于各種業務化集合同化系統中，得到了普遍認可。由于模式集合成員的數量非常有限，在計算背景誤差協方差和增益矩陣的過程中往往會出現由于樣本不足而造成的虛假遠距離相關，造成錯誤的同化更新。通過引入局地化可以使得同化的更新過程在一個較小子空間中進行，從而抑制這種虛假相關，并大大降低計算量。利用相似的思想，最近的一些工作開始在粒子濾波器中使用局地化，例如，Poterjoy[13]、Shen等[15]、Penny和Miyoshi[8]改善的局地化粒子濾波器已經被初步驗證能夠使用與集合卡爾曼濾波器相當的集合成員數來避免粒子退化現象，也逐漸地被用于地球物理模式的資料同化中。

本文在耦合的通用地球系統模式（Community Earth System Modal,CESM）中開展了集合卡爾曼濾波器和局地化粒子濾波器的觀測系統模擬試驗。通過同化模擬的衛星海表溫度（SST）資料，考察不同局地化參數對于兩種濾波器方法的不同影響。在此基礎上，進一步比較了兩種濾波器方法的同化效果，探討了兩類方法的優缺點以及發展前景。

2 數據與方法

2.1 模式和同化系統

實驗使用的模式為CESM，它是由美國國家大氣研究中心（NCAR）于2010年發布的新一代地球系統模式，是目前最先進、使用最廣泛的地球系統模式之一。該模式采用模塊化框架，主體由大氣、海洋、陸地、海冰、河流等幾大模塊組成，并由耦合器（CPL7）管理模塊間的數據信息交換和模式運行。實驗使用了CESM1.2.1版本，它的海洋模式為POP2，大氣模式為CAM4。本實驗使用全耦合的模式設置（B compset）和當代（present day）的外強迫。采用的模式分辨率為0.9×1.25_gx1v6，即大氣模式水平分辨率為 0.9°×1.25°，垂向26層；海洋模式水平分辨率接近1°，在赤道區域緯向加密約為0.5°，垂向60層。

實驗所涉及的兩種同化方法都是借助NCAR開發的資料同化 研究 平臺（Data Assimilation Research Testbed，DART）實現。DART是由NCAR的數據同化研究部門開發和維護的一個開源軟件。它提供了多種確定性和隨機性濾波器算法，包括集合調整卡爾曼濾波器、集合卡爾曼濾波器、核濾波器和粒子濾波器等[16]。我們建立了DART和POP2模式的接口，實現了耦合模式框架下的海洋觀測資料的弱耦合同化。鑒于計算量的考慮，我們使用了20個集合成員。在所有的實驗中，我們也采用了固定系數為1.02的協方差膨脹和針對20個集合成員的樣本誤差訂正（Sampling Error Correction）方案[17]。

2.2 數據

本文采用的實驗方案為觀測系統模擬試驗（OSSE），其基本思想是使用一組真值實驗作為參考值，然后根據實際存在的觀測系統對真值取樣，并且疊加上具有給定方差的隨機誤差來模擬觀測。在實驗中同化上述模擬的觀測資料，并利用真值實驗得到的參考值來評估不同同化方法得到的分析場。

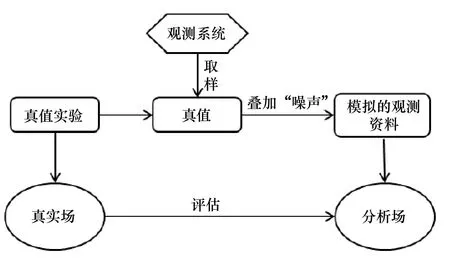
圖1 觀測系統模擬試驗流程圖設計Fig.1 Flow chart design of observation system simulation experiment

圖1顯示了OSSE的流程圖，其中我們利用真值實驗生成每周一次的全球海表溫度觀測，其空間分辨率為1°×1°，并疊加上符合高斯分布的隨機誤差作為觀測誤差。為簡化討論，我們針對所有觀測點使用相同的觀測誤差標準差。參考OISST[18]中的SST觀測誤差的全球平均標準差，假設所有位置的誤差標準差均為0.3℃。

此外，本文使用了哈德雷中心（Met Office Hadley Center）提供的長度為 100 a（1919–2018）的月平均HadISST (Hadley Centre Sea Ice and Sea Surface Temperature data set)再分析資料[19]，主要用于計算 SST 資料對不同距離的變量的相關系數，并與模式20個集合成員計算的樣本相關系數進行比較，為局地化系數的選取提供理論依據（見3.1.2節）。

2.3 同化方法和局地化

2.3.1 EAKF 中的局地化

集合調整卡爾曼濾波器（EAKF）[4]是在集合卡爾曼濾波器[2]的基礎上發展起來的。EAKF避免了集合卡爾曼濾波器中對觀測資料的擾動，且在集合樣本數目較少時仍能得到較為滿意的結果。EAKF基于線性回歸理論逐個順次地同化觀測資料，使用觀測空間的局地化后可以將每個觀測點的更新范圍限制在一個較小的子空間中進行，節省了計算量。

EAKF的同化步驟可以表示如下，若用x表示狀態向量，用yo表示誤差方差為的觀測標量，h表示觀測算子，則EAKF公式的第一步是使用觀測算子h將狀態空間的每個集合成員投影到觀測點上，作為每個成員對應觀測的先驗估計，如下

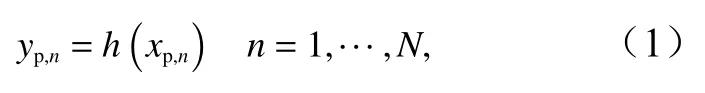
式中，下標p代表先驗值；n代表集合成員

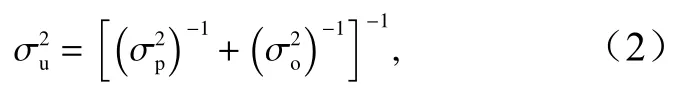
式中，下標u代表后驗值

接著使用以下公式計算觀測空間的每個成員的后驗估計

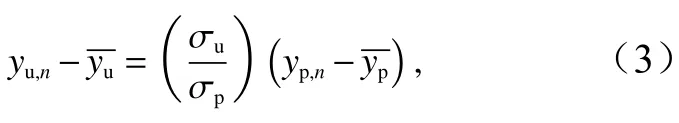
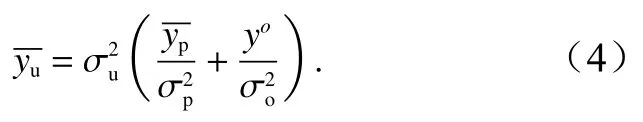
EAKF最后利用相關系數將每個觀測的增量回歸到模式變量中

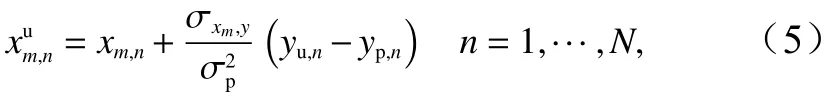
式中，xm,n表示模式第m個分量的第n個集合成員；σxm,y為xm與yp的協方差。

由于集合模式成員數有限，因此所模擬的背景誤差協方差會存在一定的虛假信息。這些虛假信息隨著距離的增加而增加，且會在同化過程中造成虛假的更新量，影響結果的準確性。為了避免這些問題，我們在EAKF中引入了局地化方案，使用一個數值介于0和1之間且隨距離的大小單調遞減的因子 ρ，并將式（5）替換為

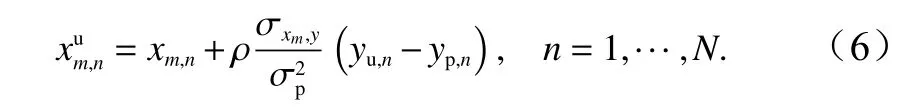
公式（6）中的 ρ被稱為局地化因子，是一個依賴于距離的函數，一般可以由以下公式[20]計算得到

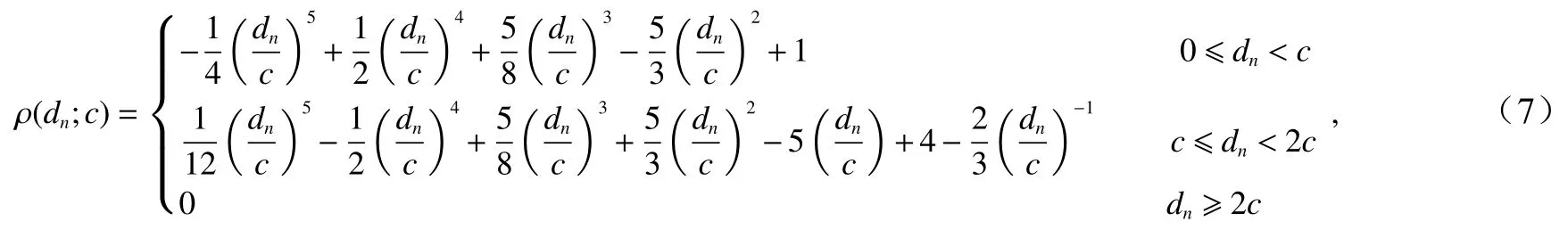
式中，dn代表模式點xm,n和觀測點yp,n的距離；c是一個局地化參數，可以控制 ρ的去相關距離。由式（7）可知，當dn大 于2c時， ρ =0，從而觀測點yp,n和模式點xm,n完全不 相關。

2.3.2 LPF 中的局地化

相比于EAKF，局地化的粒子濾波器（LPF）最近才被提出來解決傳統粒子濾波器中的退化問題[13]，因此關于它的研究結果相對較少。在作者所了解的文獻中，目前尚沒有將LPF應用于CESM模式的研究也鮮有對LPF的局地化參數進行的討論。

從原理上說，在粒子濾波器中采用局地化是為了使用較小的計算成本來避免濾波退化問題。粒子濾波器的原理是給每個集合成員配給一個權重，用集合成員的加權組合來表示同化變量的完整概率分布密度函數，并隨著同化的進行不斷更新權重。經典的粒子濾波器使用一個標量的數來代表權重，因此當模式的狀態變量維數巨大時，很容易造成其中一個成員占據大部分權重，而其他成員權重都幾乎為0的現象這就是濾波退化[2]。

在經典粒子濾波器中，狀態場Xn的標量權重可由以下公式計算

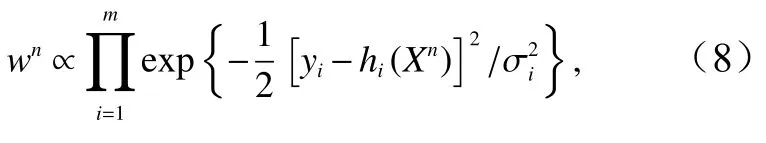
式中，wn表示第n個粒子的標量權重；m是所有觀測點的總數；觀測算子hi用 于將模式預報場投影到其中的某個觀測點yi上；是 yi的 方差，這里的正比例符號“∝”意味著計算等式右邊之后還需要進行一次標準化使得所有權重的和為1。當m很大時，多個指數函數相乘導致不同粒子的權重很容易有量級上的差異。

在粒子濾波器中引入局地化的基礎是將粒子的權重擴展成為矢量，即不同的模式網格點使用不同的權重。在此基礎上應用粒子濾波器可以將狀態分析過程轉移到一個較小子空間中進行，由于子空間的差異性會增加集合成員的多樣性，從而降低集合退化的可能。粒子濾波器中的局地化主要用于計算矢量權重，使其適用于大型地球物理模式。但是由于粒子濾波器的同化原理與卡爾曼濾波器有本質的不同，局地化的引入方式也有所不同[21]。局地化粒子濾波器的第一步是將式（8）中的標量權重擴展到矢量權重，也就是說狀態場中各個不同的分量采用不同的局部權重，與此同時，集合成員的重取樣也都在局地進行。Poterjoy[13]借助局地化公式，利用局地化因子 ρ給出不同分量的權重公式如下

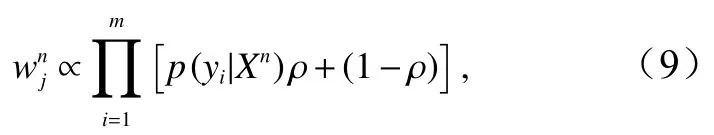
2.4 同化實驗設計

本文首先通過敏感性實驗考察局地化參數對于EAKF和LPF的同化效果的影響。局地化的參數數值對應了觀測點和模式網格點的去相關距離：假設局地化參數的值為c，那么觀測點與距離2c以上的模式網格點的相關系數為0。CESM模式中的距離使用弧度制單位表示，例如d=0.1 rad，那么它實際對應的赤道經度為為了處理海洋在垂直和水平方向的不同尺度，同化算法使用一個垂向歸一化尺度系數（Vertical Normalization Factor，以下記做ν，單位為m/rad）來進行垂向距離的轉化。假設水平方向的距離為dh，單位為（°），垂直方向的距離為dv，單位為m，那么兩點之間的模式距離如下計算

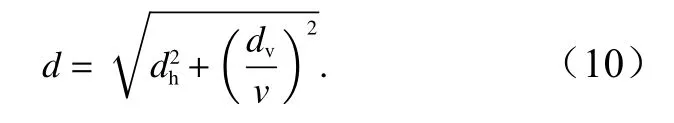
根據d和c的比值，可以使用式（7）計算局地化因子 ρ 。顯然ν的數值越大，相同的實際垂向距離dv條件下式（10）右端的第二項越小，相同的c可以影響到越遠的水平距離。而當ν為無窮大的時候，實際上就關閉了垂直方向的局地化，局地化因子僅由dh決定。

實驗所選取的同化數據為海表溫度，集合成員數為20，同化頻率為每7 d同化一次，同化實驗的時間為12個月。同化的初始集合由如下方法產生：我們首先對CESM模式進行了100 a的自由積分，然后在得到的初始場上層30層溫度變量上疊加偽隨機場[22]的擾動，構成20個集合成員。我們對該集合進行2 a的模式積分，使得每個集合成員各變量之間保持一定的動力平衡，這些積分的結果則被用來作為同化實驗的初始集合。

設計的敏感性實驗如表1所示：我們首先考察EAKF中的局地化方案，比較了不同局地化參數c和垂向歸一化尺度系數ν對于同化效果的影響。我們先固定c為 0.1 rad，然后分別設定ν=1 000 m/rad,1 500 m/rad 2 000 m/rad，以及+∞（即垂直方向不采用局地化）來考察垂向局地化方案對于同化效果的影響。并且分別將實驗名稱記作Kc0.1v1000、Kc0.1v1500、Kc0.1v2000以及Kc0.1vinf。根據CESM氣候模式的距離設置Kc0.1v1000試驗中，觀測點在海表與水平距離超過大約11.5°的模式格點相關系數為0，同時與其正下方垂直距離超過200 m的模式格點相關系數也為0。然后，我們固定最優垂向歸一化尺度系數ν，來考察水平局地化方案對同化效果的影響。由于前一組實驗得出的結論為EAKF的最優垂向局地化方案為垂向關閉局地化（見3.1.1節），在此基礎上，分別設置局地化參數c為 0.05 rad、0.1 rad、0.2 rad、0.3 rad，分別將對應的實驗名稱記為Kc0.05vinf、Kc0.1vinf、Kc0.2vinf Kc0.3vinf。類似地，我們也針對LPF探討了系數ν和參數c的相關問題，利用敏感性實驗尋找最優的局地化方案，揭示LPF和EAKF對于局地化的不同要求最后，基于使用最優的局地化方案，我們比較了LPF和EAKF的同化效果，揭示LPF的潛在優勢與不足同時，為了顯示同化效果，本實驗設置了不進行任何同化的控制試驗(下文簡稱FREERUN)進行對照。

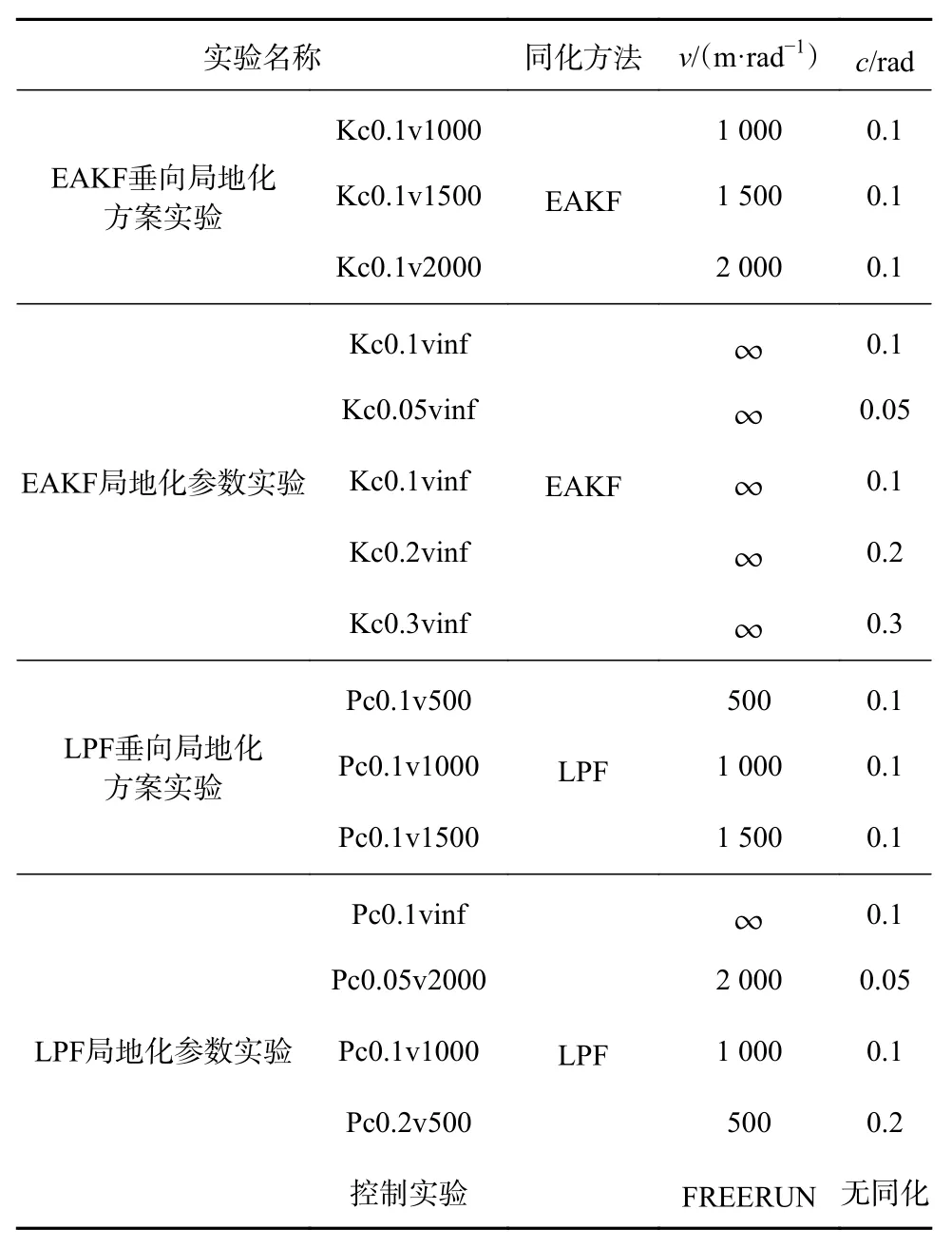
表1 實驗列表Table 1 Experimental list

3 實驗結果與討論

3.1 EAKF 局地化對同化效果影響

3.1.1 EAKF 的垂向局地化方案

我們首先固定局地化參數c為0.1 rad，考察不同垂向歸一化尺度系數ν對于同化效果的影響。實驗采用的系數ν為 1 000 m/rad、1 500 m/rad、2 000 m/rad與局地化參數c相乘以后，對應的距離分別為100 m 150 m/200 m，也就是說，局地化系數ρ在超過 200 m 300 m/400 m 的數值為 0，因此，SST 觀測最多能影響的垂直深度為 200 m/300 m/400 m。實驗選取了均方根誤差（RMSE）作為評判同化效果優劣的標準，其計算公式為

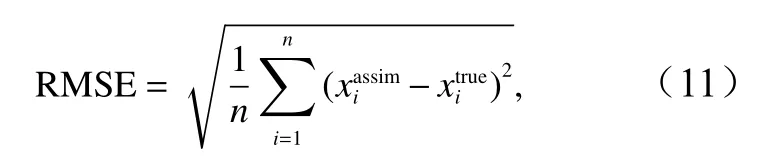
我們首先根據RMSE的垂直分布討論系數ν對同化效果的影響。圖2為設置不同ν時，EAKF同化SST資料后的垂向溫鹽RMSE。由于同化資料為SST，因此溫度的同化效果要明顯強于鹽度的，在深度較淺時其優勢更加顯著。對于溫度變量，使用不同的系數ν同化SST得到的RMSE在100 m以淺并沒有顯著差異，且都遠小于控制實驗的RMSE。而隨著深度的增加，變量與觀測之間的距離增大，一方面所有實驗的同化效果逐漸削弱，另一方面不同實驗的RMSE出現差異。特別地，當深度約為150～300 m時，在關閉垂向局地化的Kc0.1vinf實驗產生的RMSE是最小的。根據式（6）可知，EAKF利用SST更新深層溫度變量的原理是使用SST和給定層溫度之間的相關性將表層的觀測增量回歸到深層。因為深層溫度的離散度（標準差）很小，僅有O（10?2），所以即使只使用20個集合成員計算相關系數，表層和深層的相關系數也能夠正確表達。所以，雖然Kc0.1vinf實驗沒有引入垂向局地化，較深層的溫度也能夠得到正確更新。

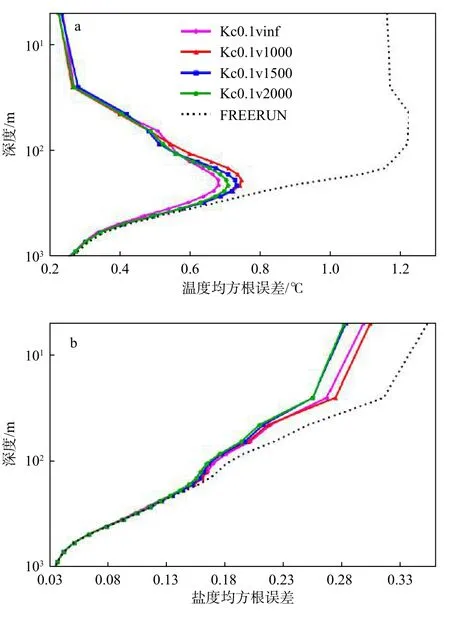
圖2 不同垂向局地化方案 EAKF 實驗中區域平均（60°S～60°N，環地球）垂向均方根誤差Fig.2 Regional mean (60°S?60°N,ring the earth) root mean square error in EAKF experiments with different vertical localization schemes

另一方面，同化SST對于鹽度的改進基于溫鹽相關得到。在150 m以淺，仍然可以發現鹽度變量的RMSE小于控制實驗的RMSE，但是不同垂直局地化方案對于鹽度同化效果的差異主要在較淺層而非深層出現。同時，圖2b的結果表明同化SST時ν=1 500 m/rad/2 000 m/rad的局地化能更好地改進淺層的鹽度，由式（10）可知，在局地化參數c固定的條件下，對于淺層的變量，尺度系數ν越大，dh起到的作用也相對越大。體現在鹽度上就是相同深度的鹽度變量獲取海表觀測的信息就越多。所以我們可以斷言，淺層的鹽度同化差異實際上受到水平局地化的影響更大綜合兩者的討論，在垂直方向不采用局地化是相對更優的方案。

3.1.2 EAKF 局地化參數

對EAKF垂直局地化方案的敏感實驗結果顯示，EAKF的同化效果在關閉垂直方向的局地化時相對較好。因此，我們在關閉垂直局地化的基礎上，分析不同參數c對應的水平局地化方案對EAKF同化效果的影響，第2組實驗采用的局地化參數分別為0.05 rad、0.1 rad、0.2 rad、0.3 rad。圖 3 從時間尺度上分析各物理量RMSE的變化情況。首先分析表層溫度、鹽度（SSS）和海表高度（SSH）變量的RMSE變化情況，如圖3a所示，SST從啟用同化的第2個月開始就一直保持較小的RMSE，且使用不同參數實驗的結果沒有明顯差異。這是由于SST的觀測資料比較密集，即使在某個點的同化中引入虛假更新，也很容易被其他點的正確更新所抵消。而對其他兩個變量來說，同化SST并不能立刻減小誤差，需要進行一段時間的持續同化和模式積分，誤差才能顯著減小，這點對于SSS特別明顯。圖3b顯示，SSS的RMSE尚處于下降階段，沒有達到穩定，其同化效果與局地化參數的大小并沒有明顯的相關關系，在最后3個月，幾種參數實驗的結果沒有顯著差別。而SSH在局地化參數稍大時同化效果較好，這說明SST和SSH之間的相關性較好，不容易產生虛假相關。

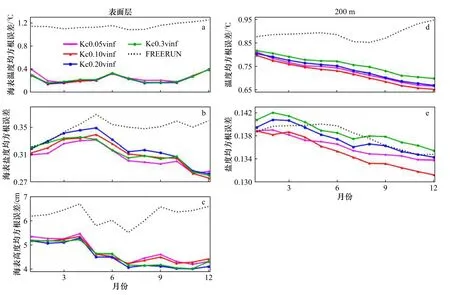
圖3 不同局地化參數 EAKF 實驗中區域平均（60°S～60°N，環地球）的均方根誤差時間序列Fig.3 RMSE time series of regional mean (60°S?60°N,ring the earth) in EAKF experiments with different local parameters

我們進一步分析較深層的同化效果發現，當深度為200 m時，圖3d和圖3e表現出最優同化效果的局地化參數c=0.1 rad。這是因為我們關閉了垂向局地化功能，因而使得一定水平距離之外的海表觀測資料能夠無差別地影響整個水柱，隨著深度的增加，實際的距離增大，遠距離觀測帶來的虛假相關也會出現。從溫度和鹽度兩個變量，都可以看出c=0.1 rad的同化效果好于c=0.05 rad，這是因為更多的觀測資料被用來更新200 m深度的變量；而它的同化效果也好于局地化參數更大的另外兩個實驗，這是因為后兩者會因為虛假相關而帶來虛假的更新。

由于集合濾波器的集合成員數量有限，在相距較遠的兩個點之間會產生虛假的相關，造成錯誤的更新，這是在EAKF中引入局地化的主要原因。因此，如果可以量化表示給定集合成員數可能造成的虛假相關，就可以相應地選擇最優的局地化參數。針對某個給定點上的觀測，以1月的控制實驗預報值為例，我們使用以下公式定義對應局地化參數c的虛假相關占比（Spurious Correlation Ratio,SCR）

圖4為SST相關系數的空間分布，我們分別選取了位于太平洋的兩個點（0°，180°）、（20°S，120°W），位于印度洋的一個點（20°S，60°E），以及位于大西洋的一個點（20°N，40°W），計算了使用不同局地化參數下的有效相關系數，樣本相關系數和分析相關系數，分別對應圖4中的前4列、第5列以及第6列，圖中的白色區域表示相關系數小于0部分。從圖中可以看出，幾乎所有位置的樣本相關系數都大于分析相關系數，因此在某些較遠區域，樣本會夸大SST的相關性，進而引入虛假相關。我們也隨機選取了其他多個格點進行相同的計算分析，得到的結論類似。通過引入局地化算法，設置恰當的局地化半徑可以在保證近距離相關的前提下去除遠距離虛假相關，避免遠距觀測引起的錯誤更新[23]。

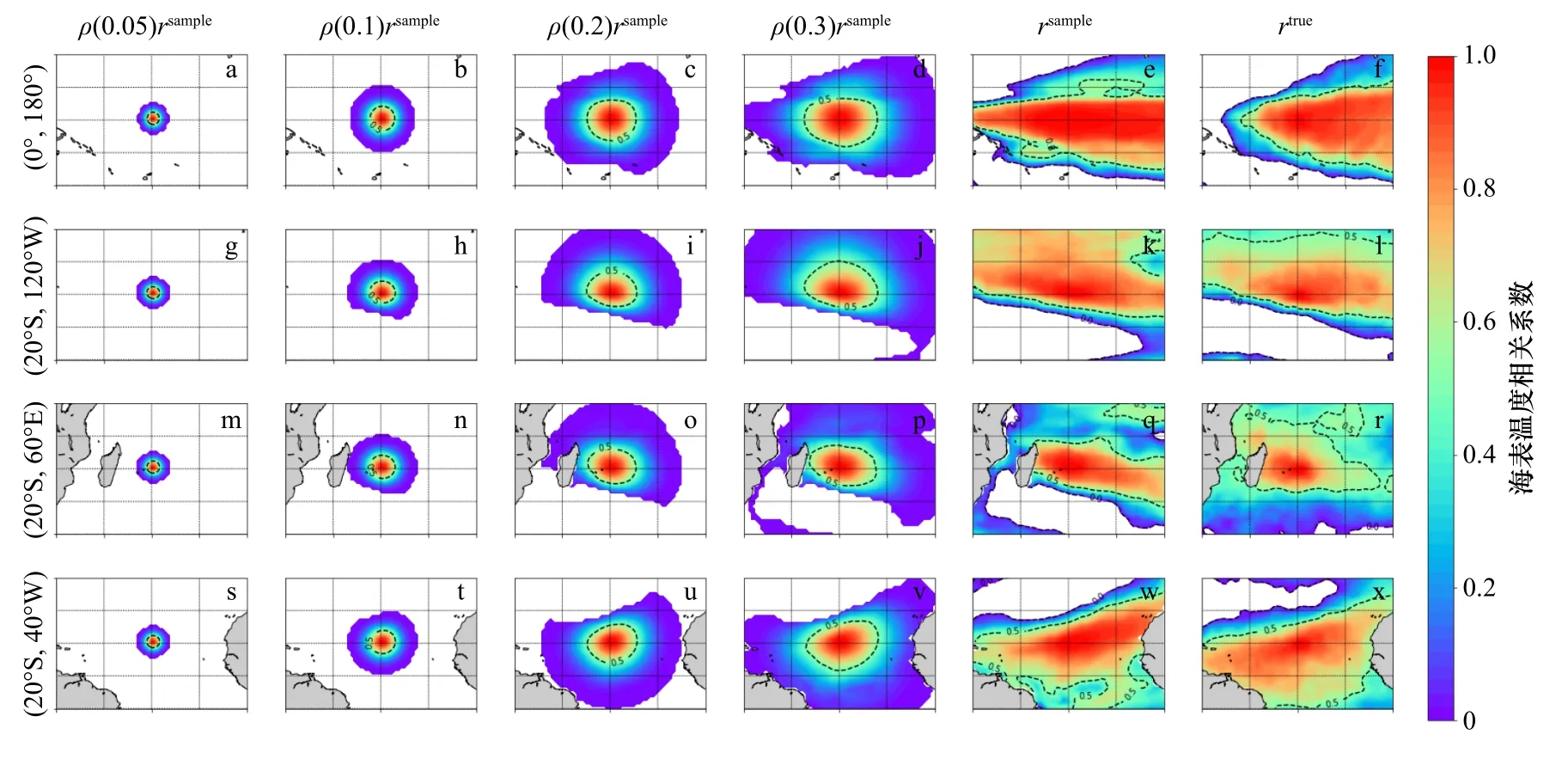
圖4 海表溫度相關系數Fig.4 Correlation coefficient of sea surface temperature

我們進一步計算了幾種不同局地化方案下的虛假相關占比（表2），發現局地化方案的引入大大減小了虛假相關的占比。其中當局地化參數c=0.1 rad時，既不會因為半徑過大而引入一些不必要的虛假相關，也不會因為局地化半徑過小而濾去大部分正確相關。因此c=0.1 rad相對而言是更優的局地化參數，與前面敏感性實驗的結果一致。

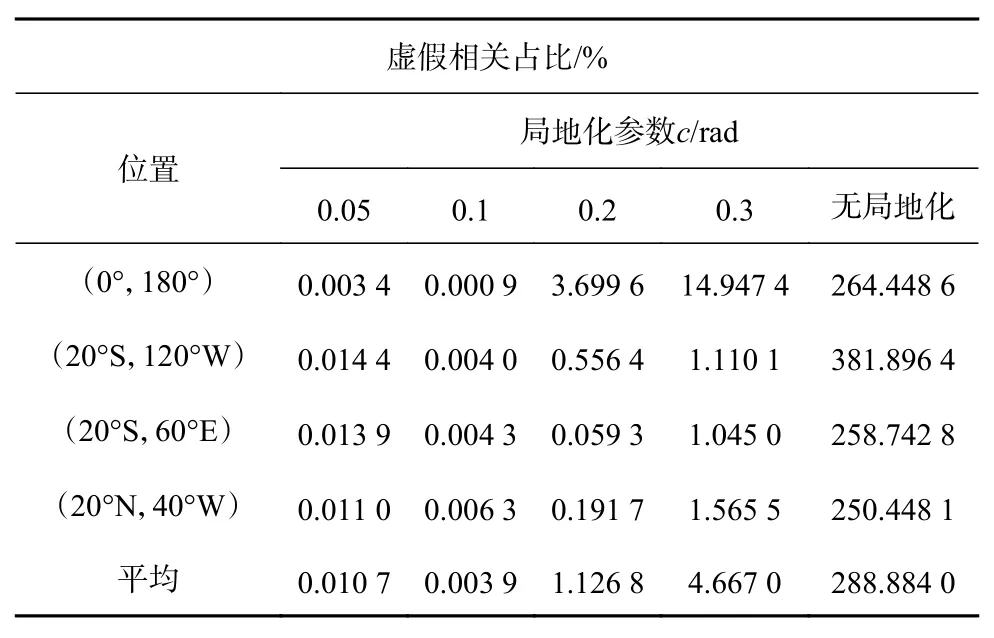
表2 SST相關系數虛假相關占比Table 2 Proportion of false correlation in SST correlation coefficient

3.2 LPF 局地化對同化效果影響

3.2.1 LPF 垂向局地化方案

第3組實驗考慮了LPF垂向局地化方案對同化效果的影響，類似EAKF局地化實驗，我們首先固定c為 0.1 rad，設置垂向歸一化系數ν=500/1000/1500/m/rad。首先，我們從海洋溫度和鹽度RMSE的垂向分布分析LPF垂直局地化對同化效果的影響。如圖5所示，在淺層，當ν=1000/1500/∞m/rad，即對應最大垂向同化距離為200 m/300 m時，LPF的同化效果較好。由式（10）可知，當局地化參數c固定，垂直距離dv較小且固定時，觀測點到它能同化到的最遠模式網格點的水平距離dh隨著v的增大而增大。在較淺的深度，v的值越大就能在水平方向取得越多的觀測資料來計算權重，如果不發生退化，就能獲得越好的同化效果。而當深度較大時，無論對于溫度還是鹽度來說，都可以發現關閉垂向局地化的LPF的效果較差，甚至會造成負面同化效果—即同化后的誤差反而大于控制實驗（例如大于500 m的溫度誤差）。這是由于粒子濾波器依賴權重的計算和重采樣來更新變量，關閉垂向局地化意味著所有層都會根據表層觀測計算的權重來重分配樣本，這會過度夸張表層觀測的影響范圍，從而給深層的變量帶來錯誤的更新[24]。綜合溫度和鹽度的實驗結果，可以發現當ν=1 000 m/rad，也就是垂向局地化距離為100 m時，LPF的同化效果最好。

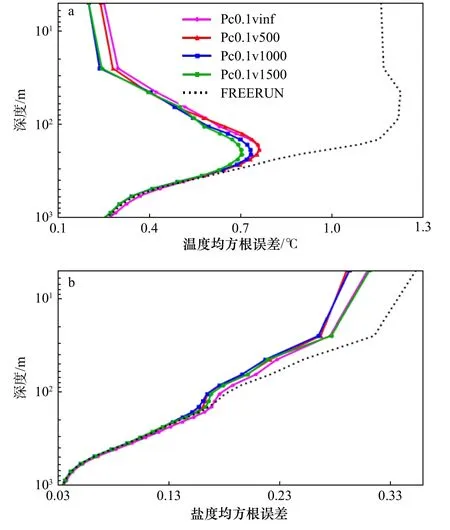
圖5 不同垂向局地化方案 LPF 實驗中區域平均（60°S～60°N，環地球）垂向均方根誤差Fig.5 Regional mean (60°S?60°N,ring the earth) root mean square error in LPF experiments with different vertical localization schemes

3.2.2 LPF 局地化參數

接下來，我們固定LPF最優垂向局地化距離為100 m，分析LPF的不同局地化參數c對同化效果的影響。由式（10）可知，考慮垂向局地化的情況下，為了保持垂直方向的局地化距離為100 m，針對不同的c需要采用不同的ν。圖6為采用不同局地化參數的LPF同化SST資料后的垂向RMSE，從圖中可以很明顯的看出，LPF的效果對局地化參數c非常敏感。當c=0.2 rad時，同化效果非常不理想，這主要是由濾波退化造成的。c的數值越大，越多的觀測能同時影響給定點的權重，從而導致該點的權重更容易退化。集合退化會大大降低粒子濾波器的效率，特別地，我們可以發現c=0.2 rad時的鹽度沒有同化效果。另一方面，當c的數值太小時，由于獲取資料過少，無法正確表達狀態變量的概率分布密度函數，也會導致同化效果不佳。圖7進一步展示了不同局地化參數得到的分析場的表層變量月平均RMSE演變，不同于圖3，即使只考慮表層變量，局地化參數對于同化效果也有很大的影響。我們可以進一步確認c=0.2 rad會導致LPF的退化。綜合圖6和圖7的結果，本實驗中最優的LPF局地化參數c=0.1 rad。

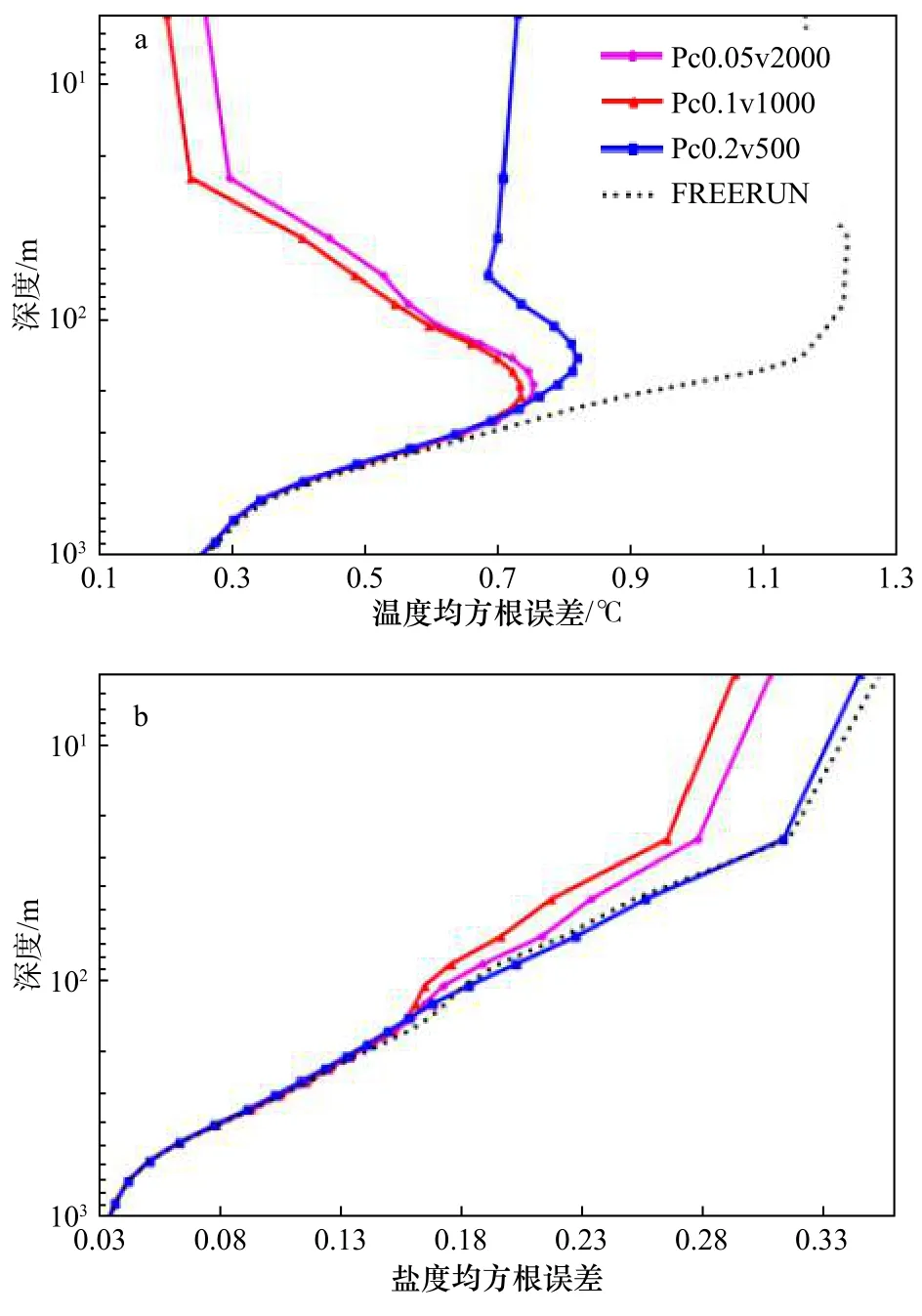
圖6 不同局地化參數 LPF 實驗中區域平均（60°S～60°N，環地球）垂向均方根誤差Fig.6 Regional mean vertical root mean square error(60°S?60°N,ring the earth) in LPF experiments with different local parameters

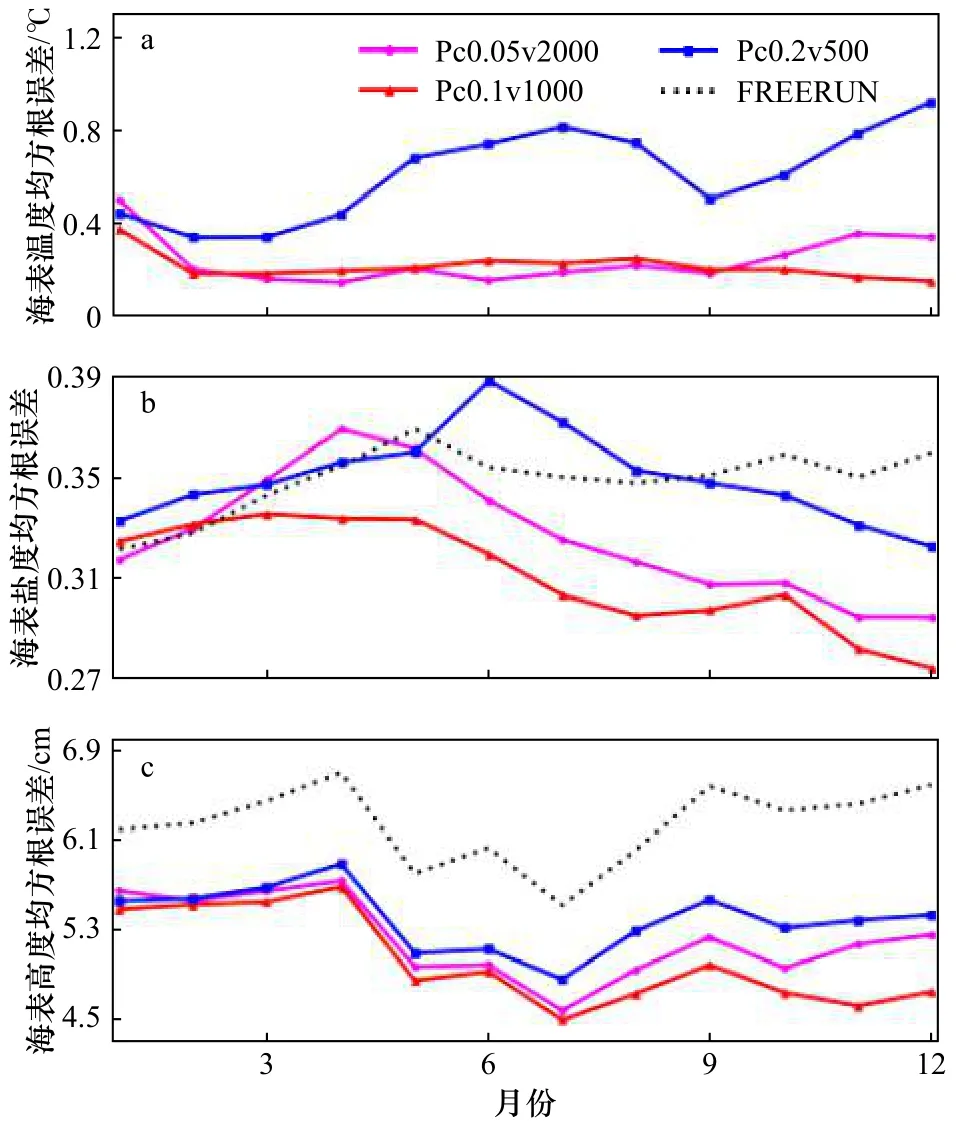
圖7 不同局地化參數 LPF 實驗中區域平均（60°S?60°N，環地球）均方根誤差時間序列Fig.7 Regional mean (60°S?60°N,ring the earth) root mean square error time series in the experiments of LPF with different local parameters

3.3 EAKF 與 LPF 的同化效果比較

最后我們采用最優局地化參數的EAKF與LPF進行對比。圖8比較了EAKF與LPF的RMSE垂向分布。從溫度RMSE可以看出，當深度小于100 m時，LPF（藍線）同化效果要優于 EAKF（紫線），但當深度在100～300 m時，EAKF同化效果要優于LPF濾波器。從前面的討論我們很容易理解這個結果，這是因為LPF需要啟用垂向局地化來避免深層的錯誤更新而EAKF在沒有垂向局地化的條件下可以通過相關系數（即使很小）來有效更新深層變量。如果EAKF也使用ν=1 000 m/rad 的局地化，其在 100 m 以下的同化效果和LPF是一樣的（紅線）。對于鹽度變量，LPF的同化效果整體要略優于EAKF，并且在淺層的效果更加明顯，這從一方面也說明溫度和鹽度的關系具有一定的非線性，因而粒子濾波器的表現更好。

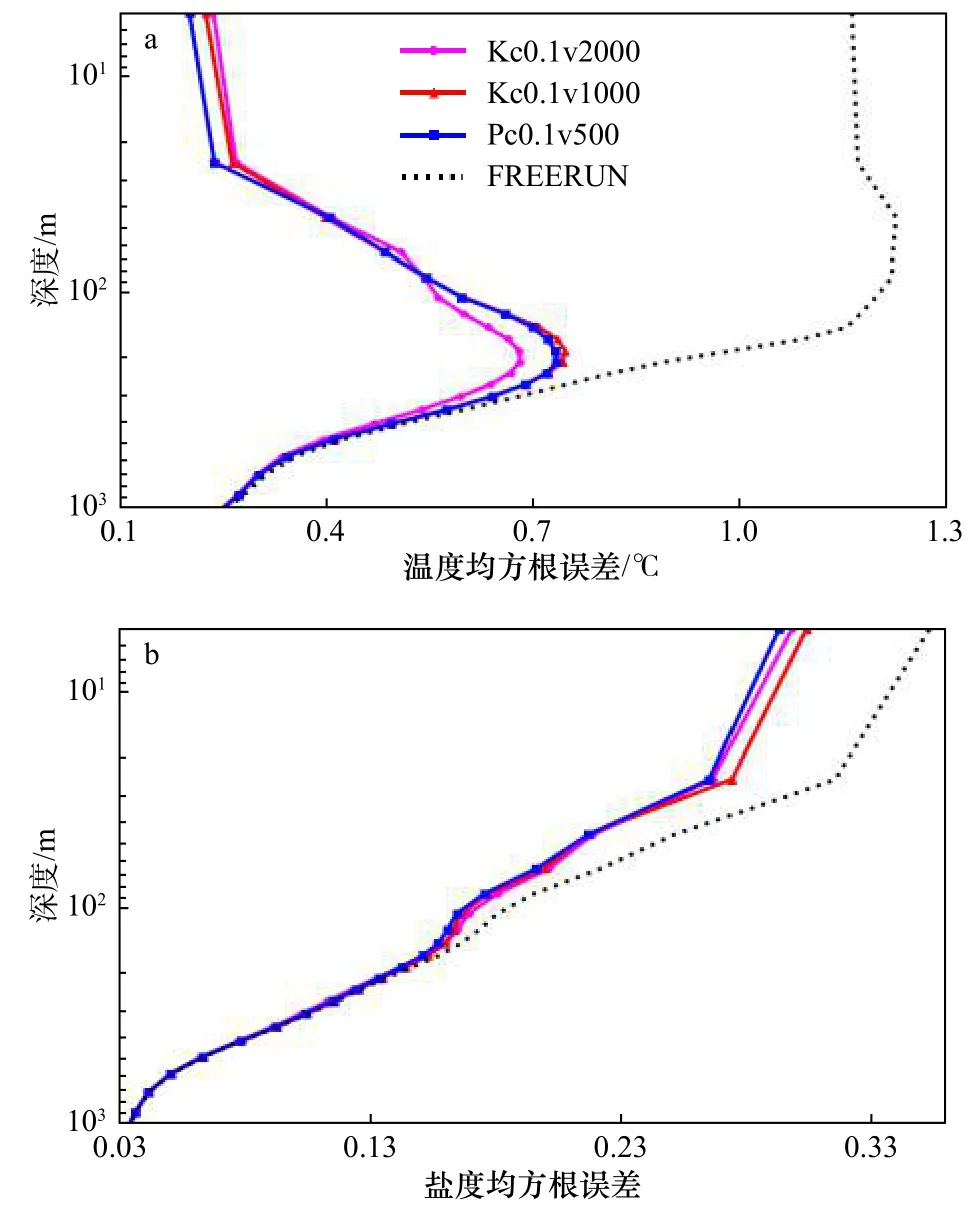
圖8 最優局地化參數 EAKF、LPF 對比實驗中區域平均（60°S～60°N，環地球）垂向均方根誤差Fig.8 Regional mean (60°S?60°N,ring the earth) vertical root mean square error in the experiments of EAKF and LPF with best local parameters

圖9為最優局地化參數的EAKF和LPF實驗的RMSE之差在海表的空間分布，其中差異由以下公式得到

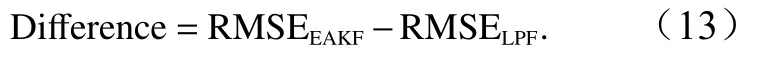
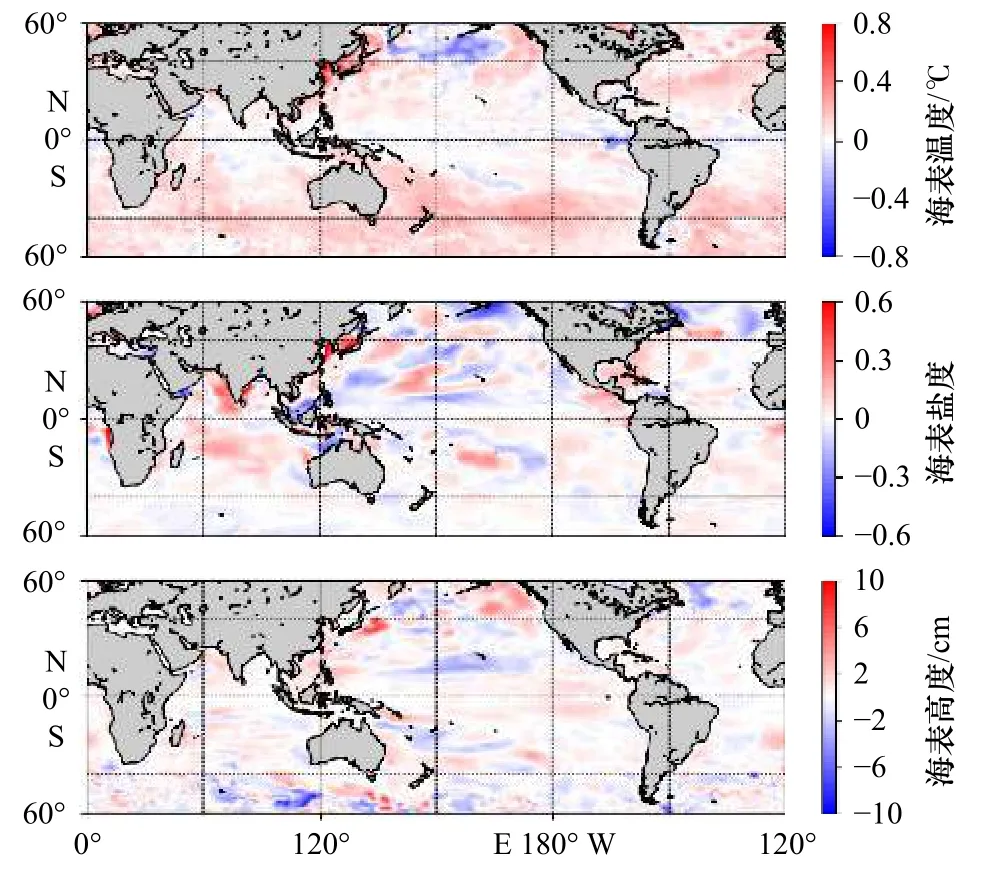
圖9 最優局地化參數 EAKF、LPF 實驗均方根誤差之差空間分布Fig.9 Spatial distribution of the difference between the root mean square error of the EAKF and LPF experiments

由定義，若它們之差大于0，則表示LPF的同化效果優于EAKF；若他們之差小于0，則相反。圖中可以明顯的看出LPF對于SST的同化效果要優于EAKF，除了北太平洋和赤道東太平洋的小部分區域外，LPF的誤差都相對較小。對于SSS和SSH來說，兩種濾波器同化效果互相有優劣。在一些典型海區（如印度洋、大西洋），LPF對鹽度同化略有優勢。而對于赤道太平洋，LPF對于SSH的同化效果更好。我們在表3進一步計算了不同區域的平均RMSE以及同化影響（Influence of Assimilation,IOA）并進行比較。其中IOA定義如下：

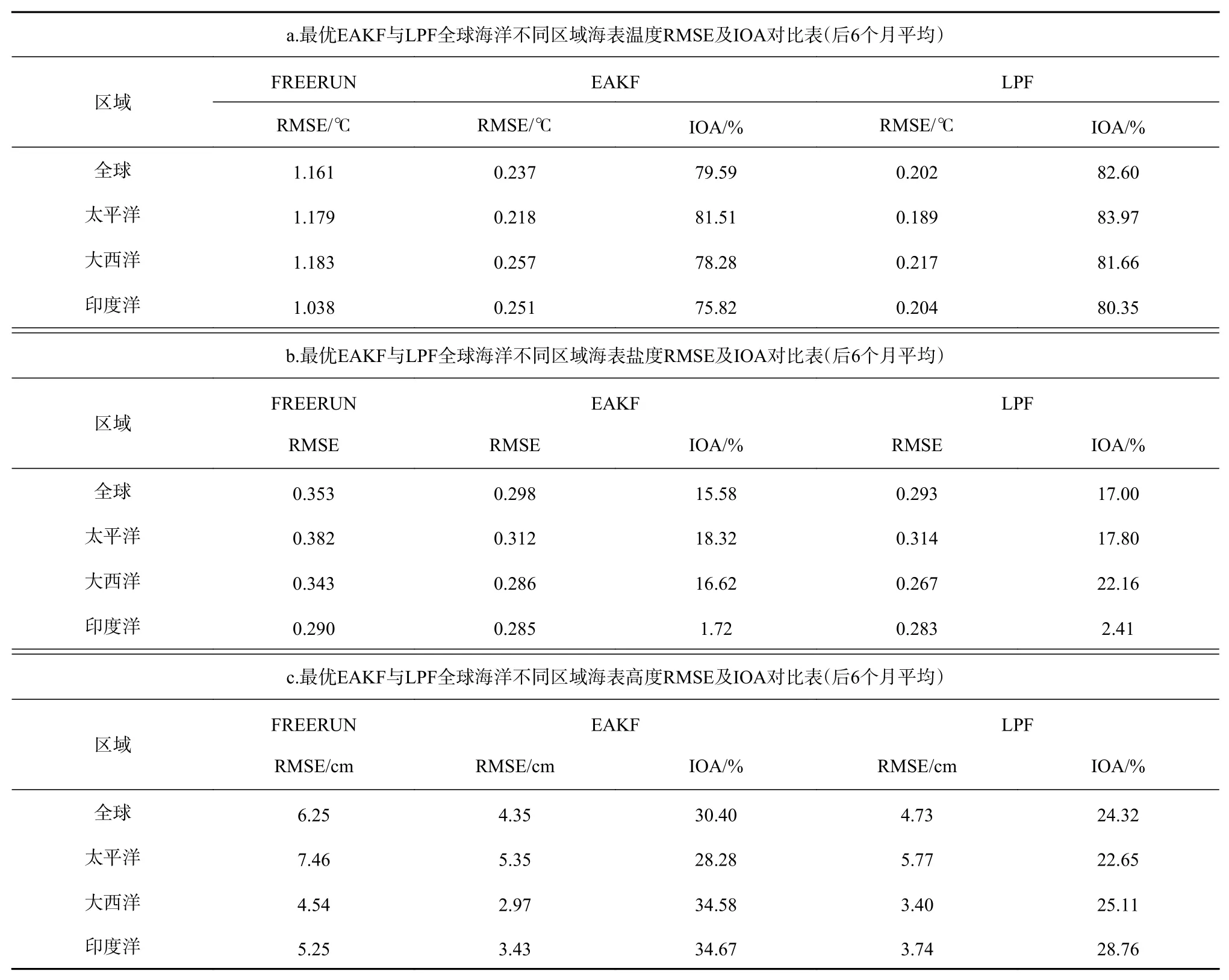
表3 最優局地化參數EAKF、LPF不同區域平均均方根誤差（RMSE）、同化影響（IOA）對比Table 3 Comparison table of mean root mean square error (RMSE) and influence of Assimilation (IOA) of EAKF and LPF in different regions

顯然LPF的SST同化效果在所有海區都優于EAKF。LPF對SSS的同化效果在印度洋和大西洋的優勢也非常顯著。而對于SSH來說，EAKF的同化效果全面優于LPF。實際上，我們發現使用集合成員有限的EAKF同化SST對于SSH的改進效果本身就不是非常顯著，其結果受到了局地化以外的很多其他因素（如平均動力地形MDT，集合離散度，跨變量相關系數等）的影響，因此還需要更多的研究來進一步解釋兩種不同同化格式對于SSH的同化效果差異。

4 討論與展望

本文在大型地球系統模式CESM中開展了SST資料的同化實驗。考察了局地化方案和參數對于集合調整卡爾曼濾波器和局地化粒子濾波器兩種同化方法的效果的影響，并對兩種方法進行了比較。

其中，集合卡爾曼濾波器使用變量之間的相關性來傳遞觀測點的更新量。為此我們提出了一個虛假相關占比公式，對集合樣本的相關和真實的相關進行比較，判別局地化對于抑制遠距離虛假相關的貢獻，并以此為依據選擇局地化參數。在垂直方向，我們發現由于深層變量的集合離散度較小，在同化SST資料的時候不需要特別采用垂向局地化就能達成效果。而局地化粒子濾波器基于使用局部觀測來決定不同位置變量的權重，并利用重采樣方法進行更新，因此局地化參數對于粒子濾波器的影響更大。我們必須謹慎選擇局地化參數來避免粒子濾波器的退化，否則會產生負面的同化效果。此外我們也驗證了垂直方向的局地化對于LPF是必要的。

選用最優局地化方案的兩種濾波器的對比表明，LPF在淺層的同化效果比EAKF好，在較深層，由于垂向局地化的影響，LPF的效果略差于EAKF。由于粒子濾波器在理論上不含高斯分布假設，比較適用于非線性的系統和誤差，在實驗中LPF對于鹽度的變量的同化優勢也比較明顯。

綜上，本文驗證了粒子濾波器在全球耦合氣候模式中的可行性，強調了有效的局地化策略對于避免濾波退化和改進同化效果方面的重要性。通過與集合卡爾曼濾波器的同化效果對比，我們進一步揭示了局地化粒子濾波器這一種新興算法在未來具有非常大的潛力被應用于復雜模式的業務化同化系統中。

當前的實驗僅考慮了同化SST資料過程中的局地化方案，對于其他的觀測資料類型，如溫鹽廓線資料和海表面高度異常資料，其結論不一定相同。另一方面，當前的工作僅考慮使用20個集合成員進行計算，與局地化相關的結論也有一定的限制。我們將在下一階段的工作中，進一步考慮使用不同的濾波器對于多源海洋觀測資料的同化效果差別以及局地化方案的選擇策略，也將進一步嘗試不同集合成員數對于同化效果的影響。