波浪在局部可滲透水平海床上傳播的解析解

倪云林，滕斌

(1.大連理工大學 海岸和近海工程國家重點實驗室，遼寧 大連 116024；2.浙江海洋大學 海洋工程裝備學院，浙江 舟山 316022)

1 引言

多孔介質海床具有滲透性，當波浪在多孔介質海床上傳播時會發生波高衰減和波能損失。但是大多數的水波理論假設海底是不可滲透的，這勢必會對波浪長距離傳播的推算造成誤差，對海岸及近海工程中設計波浪要素的計算帶來影響。

關于波浪在滲透海床上傳播變形的問題，許多學者采用不同的方法開展了相關研究。其中，在實驗研究方面，Savage和Fairchild[1]開展了波浪在粗砂和細砂海床上傳播能量衰減的實驗；?zhan和Shi-Igai[2]、Gu和 Wang[3]、Sawaragi和 Deguchi[4]先后開展了不同類型的波浪在多孔介質海床上波高衰減的實驗研究。在理論研究方面，Putnam[5]基于線性波浪理論和達西定律，推導了因波浪運動產生滲流而導致波能損失的理論；Reid和 Kajiura[6]、Murray[7]、Dean和 Dalrymple[8]同樣基于線性波浪理論，深入研究了剛性、無限深多孔介質海床上波浪衰減的邊界值問題，并得到了復波數色散關系。在數值模型研究方面，主要是利用緩坡類方程[9–11]、Boussinesq 型方程[12]、Navier-Stokes方程[13–14]研究波浪與滲透潛堤的相互作用。

現有的理論研究主要針對波浪在全滲透海床上的傳播問題，且大多數只考慮了傳播模態。本文推導波浪在局部可滲透海床上傳播，包含非傳播模態的解析解，探討滲透系數、相對水深和滲透海床長度對波高衰減的影響以及局部滲透海床對波浪的反射和透射。

2 數學公式

2.1 理論推導

考慮二維笛卡爾坐標系統下波浪在局部可滲透水平海床上的傳播問題。如圖1所示，整個流域水深為常數h，海床水平且局部可滲透，其中，區域II(?L/2≤x≤L/2)海底可滲透，長度為L，其下區域IV為不可壓縮飽和多孔介質組成的無限深可滲透海床，其左側區域I(xL/2)為海底不透水的半無限長區域。選取坐標系原點為滲透海床垂直平分線與靜水位的交點，x軸水平向右為正，z軸豎直向上為正。

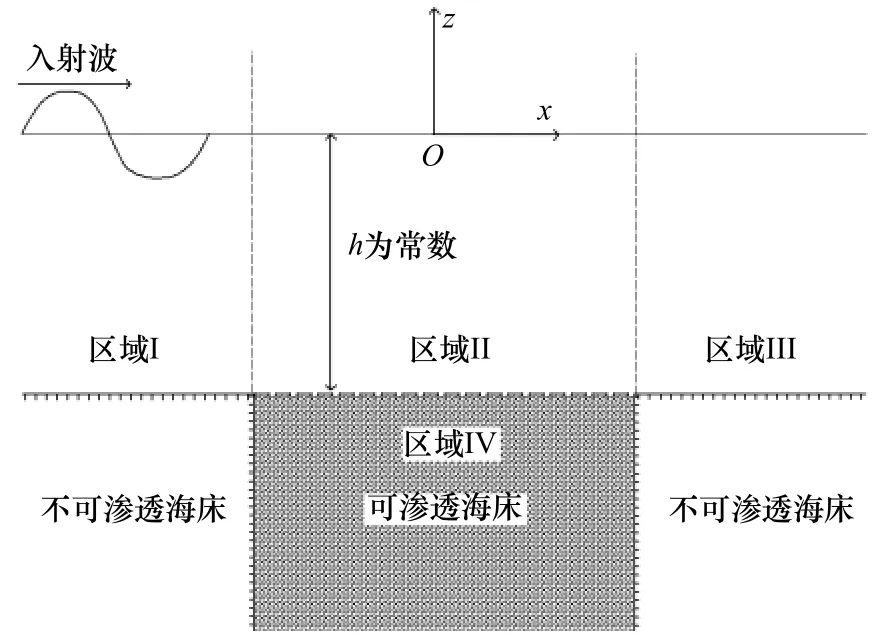
圖1 波浪在局部可滲透海床上傳播示意圖Fig.1 Definition sketch of wave propagation over a local porous seabed

假設流體為無黏、不可壓縮的均質液體，波浪運動無旋且波面升高和運動速度足夠小，則可以應用線性波浪理論。對于不可滲透海床上波浪沿x軸正方向傳播的情況，速度勢 φ (x,z)為

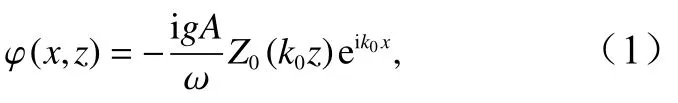
式中，A為波浪振幅；g為重力加速度；為波浪圓頻率；k0為波數。垂向特征函數Z0(k0z)=coshk0(h+z)/coshk0h，圓頻率和波數滿足色散關系

對于滲透海床上波浪沿x軸正方向傳播的情況，根據Dean和Dalrymple[8]的推導，速度勢 φp(x,z)為

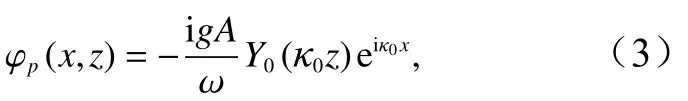
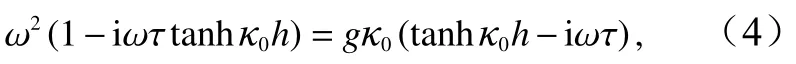
式中，κ0=κ0r+iκ0i，其實部κ0r為波數；虛部κ0i是空間衰減系數。復波數可采用Mendez和Losada[15]提出的攝動法計算。

根據Darcy定律，可滲透海床內部的滲流速度為

式中，K為海床多孔介質的滲透特性；η為水的動力黏性系數；Ps為海床中的動水壓強，滿足Laplace方程

這樣，區域I、II、III中速度勢和區域IV中的動水壓強可分別展開如下。

在區域I中

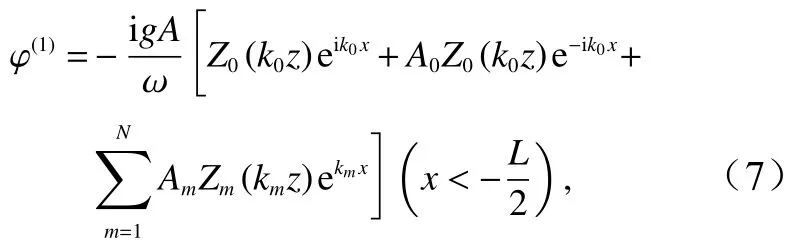
式中，Am(m=0,1,···,N)為待定系數，N為選取的項數；非傳播模態的垂向特征函數Zm(kmz)=coskm(h+z)/coskmh，km是下述色散方程的正實根

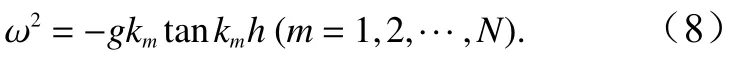
在區域Ⅱ中

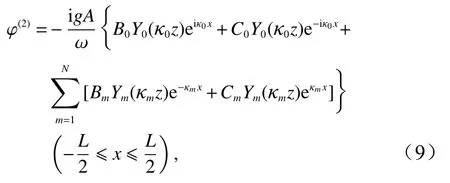
式中，Bm和Cm(m=0,1,···,N)是待定系數；非傳播模態的垂向特征函數是下述色散方程的復數根

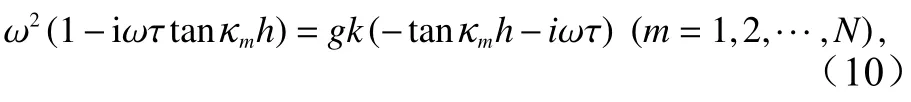
同樣可采用攝動法求解。

在區域III中

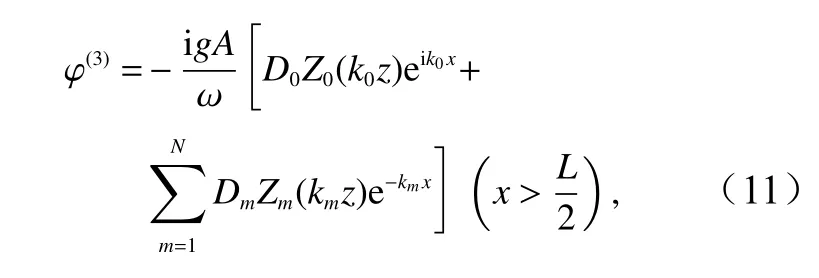
式中，Dm(m=0,1,···,N) 是待定系數。

在區域IV中

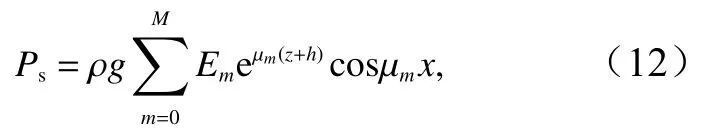
式中，Em(m=0,1,···,M) 是待定系數，M為選取的項數，μm=2mπ/L；ρ為水體密度。

速度勢和速度在區域I、II和區域II、III兩個交界面上連續的匹配條件為

將式(13)、式(14)左右兩邊同乘以Zm(kmz)(m=0,1,···,N)，并對z沿水深積分

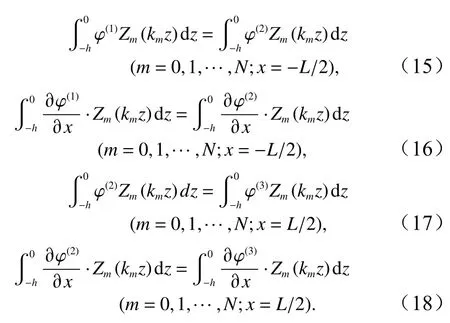
壓強和滲流速度在區域II、IV兩個交界面上連續的匹配條件為

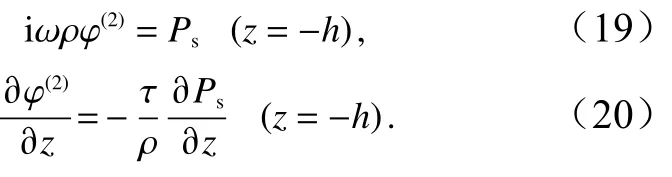
將式(19)直接對x沿滲透海床長度積分，式(20)左右兩邊同乘以 co sμmx(m=1,···,M)后對x沿滲透海床長度積分

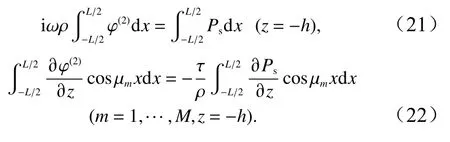
綜上可得4×N+M+5個線性方程，進而確定4×N+M+5個展開系數。

2.2 收斂性分析

本章節分析非傳播模態截斷項N和滲透海床內部動水壓強截斷項M的取值對結果收斂性的影響。關于非傳播模態截斷項N，Kirby和Dalrymple[16]指出只有N的值取足夠大，才能保證解的收斂性。他們通過研究波浪過海溝地形的問題，發現對于絕大多數的入射波而言，取N=16時就能保證收斂性，得到足夠準確的結果。這一結論被應用于Bender和Dean[17]的研究工作。本文在后續的計算中，同樣取N=16。

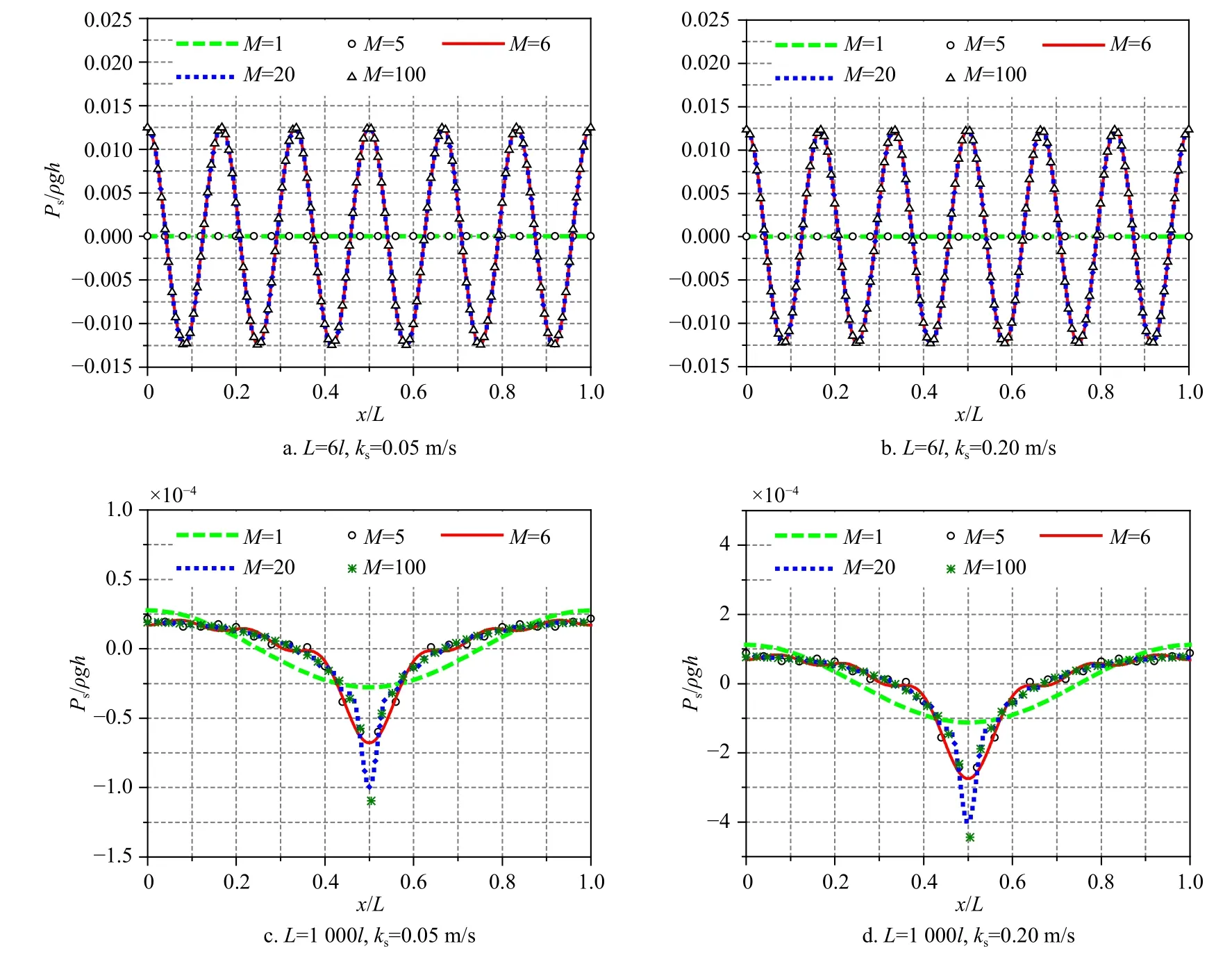
圖2 動水壓強截斷項M 取值分析Fig.2 Analysis of the value of the pore pressure truncation itemM

關于可滲透海床內部動水壓強截斷項M的取值問題，本文通過增加M的值，計算z=?h處動水壓強的變化情況，進而確定M的取值。計算時，水深h=15 m，入射波波長l=40 m（相應地波浪圓頻率ω=1.229 6 Hz），滲透海床長度分別取L=6l和L=1 000l，海床滲透系數ks分別取 0.05 m/s和 0.2 m/s，則z=?h處無量綱化的動水壓強Ps/ (ρgh)在滲透海床長度方向上（x / L）的變化情況如圖2所示。可以看出，當M=20時，z=?h處動水壓強與M=100時基本一致，本文認為取M=20就能保證可滲透海床內部動水壓的收斂性。

3 計算結果和討論

本節應用上述解析方法討論海床滲透系數ks、 相對水深h/l、滲透海床相對長度L/l這3個因素對波高衰減和波浪反射、透射的影響。

3.1 滲透系數ks的影響

在本算例中，水深h=15 m，入射波波長l=40 m（相應地波浪圓頻率ω=1.229 6 Hz），滲透海床長度L=6l。考慮到粗砂、細砂、珊瑚礁等滲透海床的滲透系數數量級介于 10?1～10?3m/s[18–19]，本算例首先計算滲透海床的滲透系數ks=0.5 m/s、0.2 m/s、0.08 m/s、0.05 m/s情況下相對波高的沿程分布；同時，為了檢查本文解析模型的普適性，也考慮了ks=0，即區域II中的海床為不可滲透的特殊情況。不同滲透系數情況下復波數計算結果見表1，相對波高如圖3所示。然后，計算反射系數Kr=|A0|和透射系數Kt=|D0|隨ks的變化情況，結果如圖4所示。

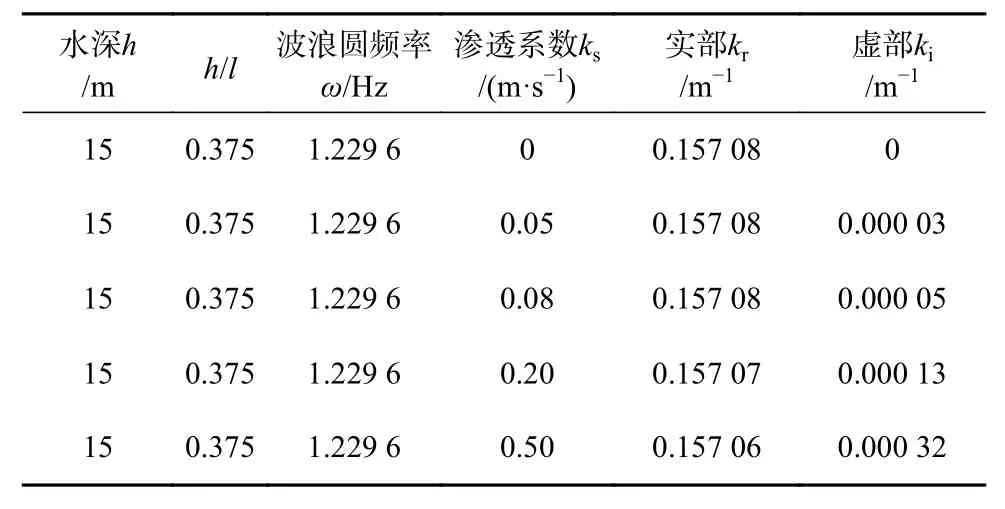
表1 不同滲透系數情況下復波數計算結果Table 1 Complex wavenumber calculated for different permeability coefficients

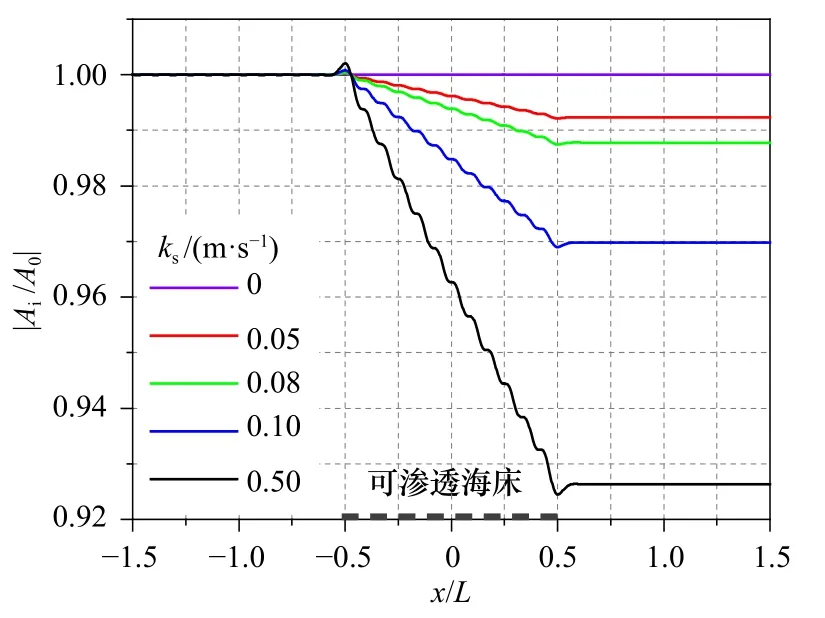
圖3 不同滲透系數情況下相對波高分布情況Fig.3 Wave height distribution for different permeability coefficients

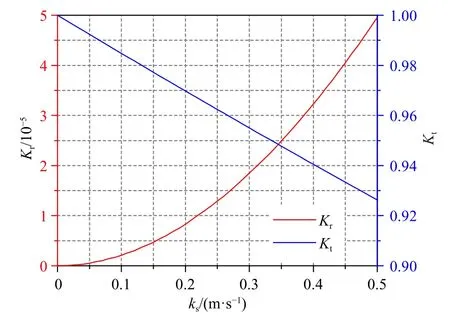
圖4 反射系數和透射系數隨滲透系數變化情況（h/l=0.375，L=6l）Fig.4 The change of reflection coefficient and transmission coefficient with permeability coefficients (h/l=0.375,L=6l)

可以看出，當ks=0時，相對波高等于1，反射系數為0，透射系數為1，即波高沿程不變；而當ks≠0時，區域I和區域II的相對波高存在波動，這是由于波浪反射造成的；波浪傳過局部可滲透海床，相對波高沿程按exp[?ki(x+L/2)](?L/2≤x≤L/2)指數趨勢衰減，滲透系數越大，復波數虛部ki也越大，相應地衰減程度也越 大，同時，局部可滲透海床對波浪的反射更強烈。

3.2 相對水深h/l的影響

在本算例中，滲透海床長度L=6l，滲透系數ks=0.5 m/s，入射波波長l=40 m。首先計算水深h=20 m、15 m、10 m，即h/l=0.5、0.375、0.25情況下相對波高的沿程分布。不同相對水深情況下復波數計算結果見表2，相對波高如圖5所示。接著，計算反射系數Kr和透射系數Kt隨h/l的變化情況，結果如圖6所示。

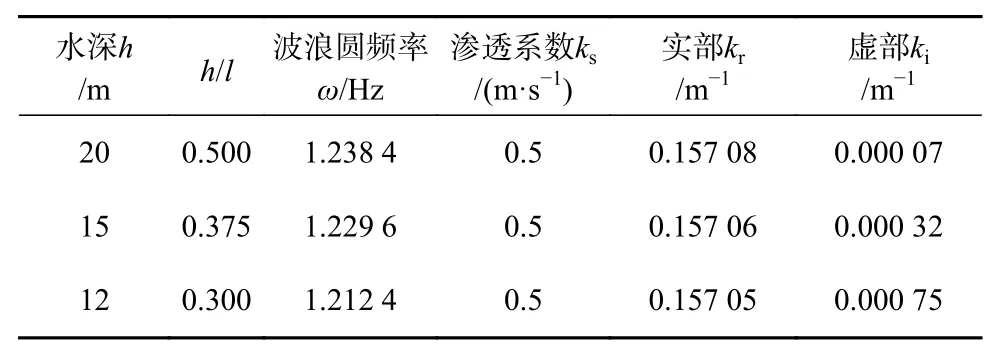
表2 不同相對水深情況下復波數計算結果Table 2 Complex wavenumber calculated for different water depth

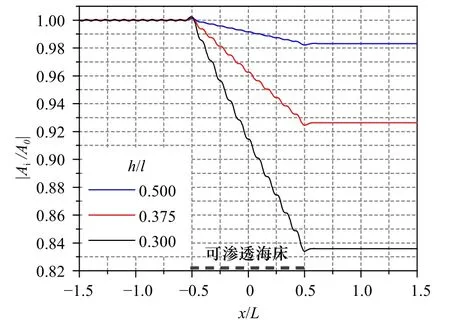
圖5 不同相對水深情況下相對振幅分布情況Fig.5 Wave height distribution for different water depth

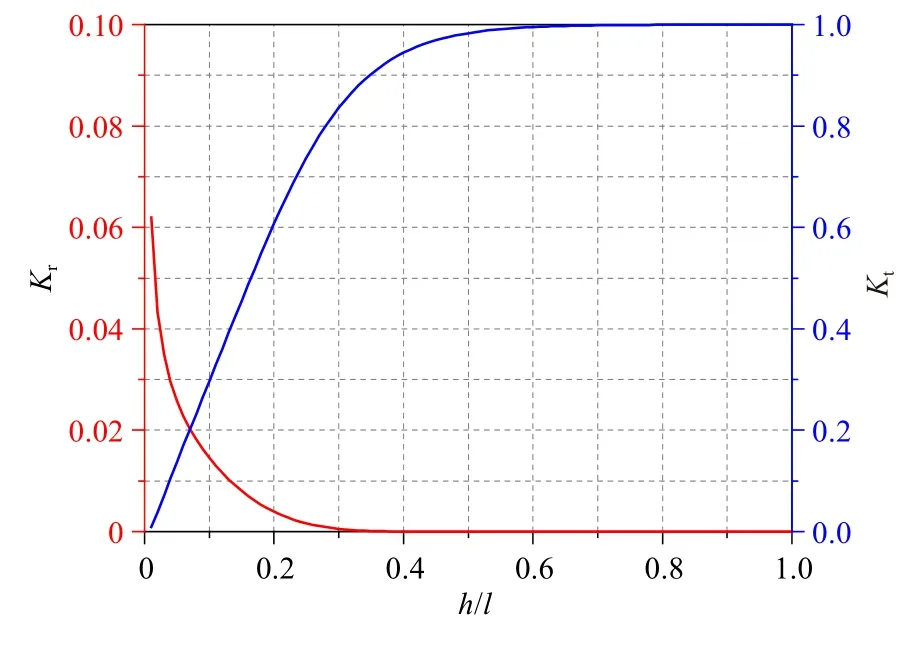
圖6 反射系數和透射系數隨相對水深變化情況（ks=0.5 m/s，L=6l）Fig.6 The change of reflection coefficient and transmission coefficient with water depth (ks=0.5 m/s,L=6l)

可以看出，隨著相對水深h/l的減小，復波數虛部ki增大，波高衰減加劇，且波動加強；反射系數隨相對水深的減小而增大，透射系數隨相對水深的減小而減小。這說明相對水深的減小增大了滲透海床對波浪的影響。

3.3 滲透海床相對長度L/l的影響

滲透海床相對長度L/l的影響主要探討反射系數Kr和透射系數Kt隨L/l的變化規律。在本算例中，水深h=15 m，入射波波長l=40 m（相應地波浪圓頻率ω=1.229 6 Hz），滲透系數ks分別取 0.10 m/s和 0.50 m/s，滲透海床長度L介于0～1 000l之間變化，則反射系數Kr和透射系數Kt的計算結果見圖7a和圖8a。為了進一步觀察變化規律，我們對滲透海床長度0≤L≤6l范圍內的計算結果進行了局部放大，結果如圖7b和圖8b所示。

從圖7可以看出，反射系數很小，但呈現出振蕩變化的規律：當滲透海床長度時，反射系數達到谷值；而當滲透海床長度2,3,4,5)時，反射系數達到峰值。隨著滲透海床長度的不斷增加，反射系數振蕩減小，并趨于常數。

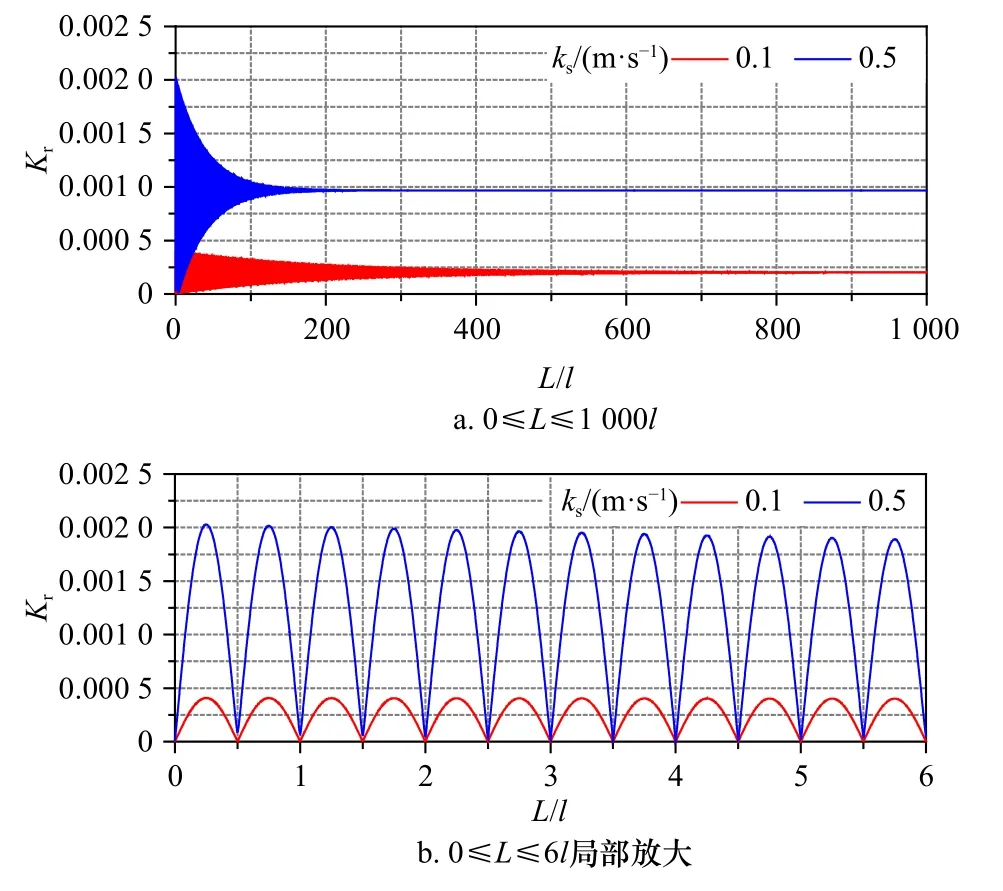
圖7 反射系數隨滲透海床相對長度變化情況Fig.7 The change of reflection coefficient with the length permeable seabed

從圖8可以看出，透射系數隨滲透海床長度的增加 而按exp(?kiL)指數減小。

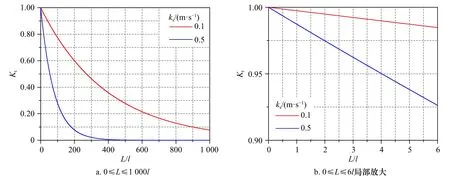
圖8 透射系數隨滲透海床相對長度變化情況Fig.8 The change of transmission coefficient with the length permeable seabed

4 結論

局部可滲透水平海床由有限長度的可滲透海床及其兩側半無限長不可滲透海床所組成，水深為常數。本文基于勢流理論，建立了線性波浪在局部可滲透海床上傳播的解析模型，研究結果表明：

（1）波浪在傳過局部可滲透海床的過程中，波高沿程衰減，衰減程度隨滲透系數的增大、相對水深的減小和滲透海床長度的增加而變大。

（2）受“海床局部可滲透”的影響，波浪發生反射和透射。反射強度小，反射系數隨滲透海床長度的變化而呈現有規律的振蕩：當滲透海床長度為入射波半波長的整數倍時，反射系數達到谷值，而當滲透海床長度為入射波1/4波長的奇數倍時，反射系數達到峰值。但隨著滲透海床長度的不斷增加，反射系數振蕩減小，并趨于常數。透射系數則隨滲透海床長度的增加而指數減小，在滲透海床足夠長的情況下，透射系數趨于0。