基于未確知測度理論的礦石合格塊度優選
馬海林,周英烈,饒斌,馬強,陳順滿
(1.中鐵隧道局集團有限公司 北京分公司,北京 100020;2.石家莊鐵道大學,河北 石家莊 050043)
0 引言
在金屬礦山地下開采中[1],礦石運輸是礦山開采的重要工藝流程之一,而礦石的合格塊度是影響礦山運輸效率的重要指標,其塊度大小是否合理對礦山的總體效益、井下作業安全程度和生產能力影響較大,因此,需綜合考慮確定礦石的合格塊度大小。如果礦石的合格塊度較大,則對礦石的運搬、運輸和提升設備提出了更高的要求,所需的投資也會大大增加,比如放礦巷道的斷面需要增大等。但礦石的合格塊度越大,所需二次破碎量越小,則破碎成本也會相應減小,同時,礦山的安全生產條件和安全效益也會顯著提高。
確定礦石的合格塊度,對減少礦山的投資,給礦山帶來最大的經濟效益,給井下創造安全的生產條件都具有很重大的意義。現場工程實踐表明,設備設施因素、技術因素和人為因素等均會影響礦石的合格塊度,但目前對礦石合格塊度影響的方法多為定性分析,而采用定量分析方法的研究相對較少。文獻[2]將多目標模糊數學的方法應用于礦石合格塊度的評價中,但這種方法在確定權重時帶有很強的主觀因素,對礦石合格塊度評價結果的影響較大。
未確知測度理論主要是通過對所需解決的問題進行分析,闡明影響研究目標的因素,采用未確知理論和數學理論,構建未確知測度理論模型,實現對工程實例的研究。該方法不同于灰色信息、隨機信息和模糊信息,是一種不確定性的信息理論,最初由王光遠教授提出。目前,該理論已廣泛應用于礦山[3-4]、管道[5]、邊坡[6]、隧道[7]、市政[8]和生態[9]等行業。該方法主要是采用熵的理論來確定權重,可避免人為主觀因素的影響,其確定權重的方法較為科學合理[3],能夠比較真實地反映各指標對研究目標的影響程度,因此,本文以某鐵礦為研究對象,采用未確知測度理論對某鐵礦的礦石合格塊度進行優選,可為類似礦山進行礦石合格塊度優選提供理論指導。
1 工程實例分析
本研究以某鐵礦為研究對象,其整個礦區的生產能力為300萬t左右,隨著社會的快速發展,人們對礦產資源的需求日益增加,這就需要提高礦山的生產能力,但礦山的總體效益對礦山的安全生產也具有重大影響。本研究以井下-395 m階段1個年產20萬t礦塊為例,通過對其進行模擬開采,對該礦區的礦石合格塊度進行未確知測度評價。
1.1 礦石合格塊度選擇評價指標體系的建立
通過對影響礦石合格塊度選取的因素進行分析,并結合礦山的實際經驗,選取鑿巖成本、爆破成本、出礦成本、運礦成本、二次破碎成本、采礦效益和安全生產條件等7項指標作為評價指標。分別用M1、M2、M3、M4、M5、M6、M7表示,其中M1、M2、M3、M4、M5、M6為數值型指標,可用精確的數值表示,M7為定性指標。結合各指標的實際情況,M1~M5為極小型指標;而M6和M7為極大型指標。
1.2 確定優選對象空間
根據某鐵礦的實際生產經驗,現有的礦石合格塊度尺寸為 400 mm,以滿足礦山生產能力、采礦效益和保證安全生產為基本前提,結合礦山的生產經驗,擬定以下6種基本方案:450 mm、500 mm、550 mm、600 mm、650 mm 和 700 mm。
1.3 評價指標等級
根據評價指標的屬性情況,可將各指標分為I、Ⅱ、Ⅲ共3個等級,分別表示優秀、良好和較差。
1.4 確定各指標的分級標準
根據現場的生產經驗以及專家的建議,各類指標的分級標準見表1。
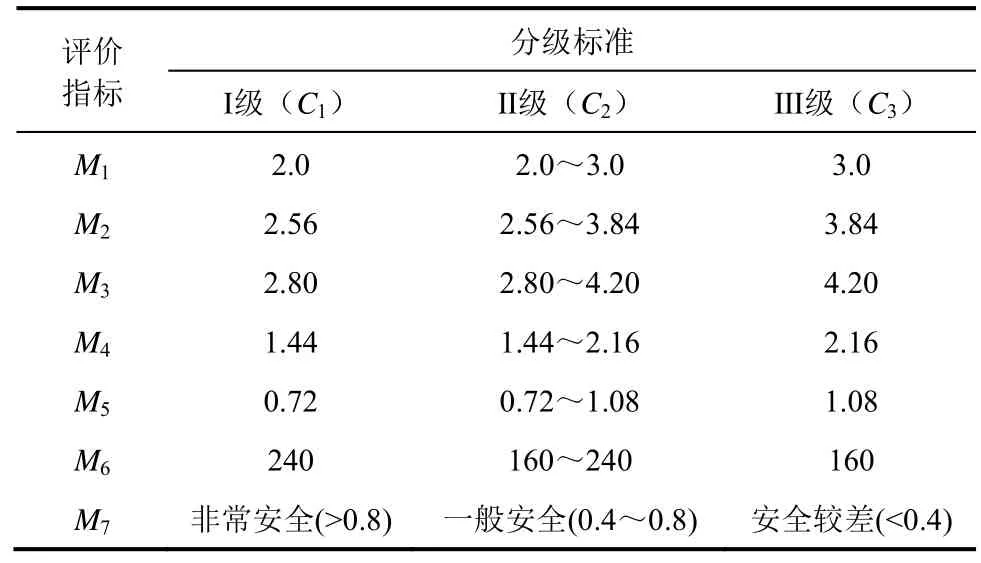
表1 優選指標分級標準及賦值
1.5 構造單指標測度函數
研究表明,單指標測度函數有指數函數分布、拋物線型分布、對數函數和直線型函數等分布形式,而直線型函數應用較為廣泛,且具有簡單、方便、高效和實用的特點,因此,構造出某鐵礦鑿巖成本、爆破成本、出礦成本、運礦成本、二次破碎成本、采礦效益和安全生產條件的單指標測度函數如圖1~圖7所示。
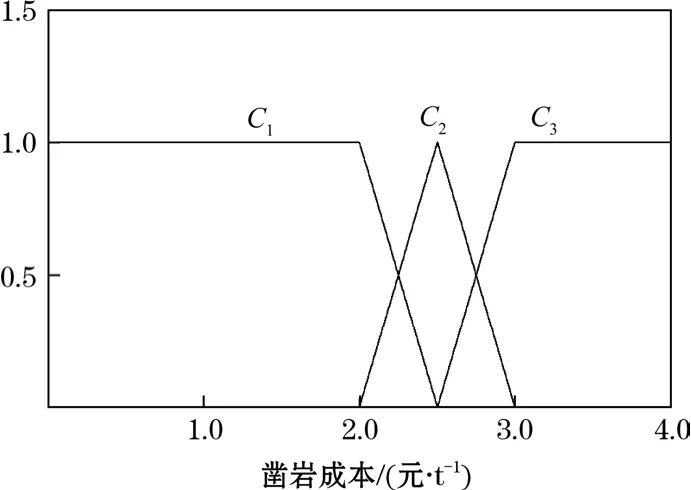
圖1 鑿巖成本單指標測度函數
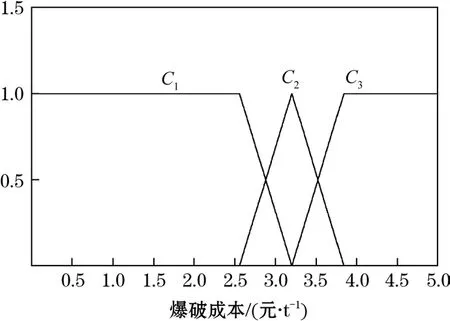
圖2 爆破成本單指標測度函數
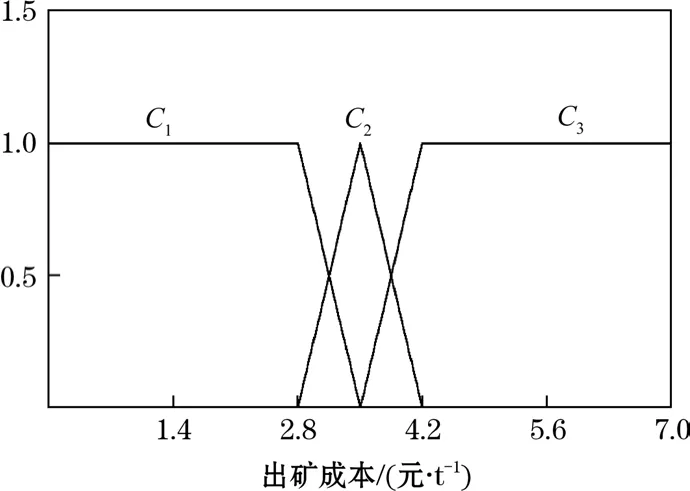
圖3 出礦成本單指標測度函數
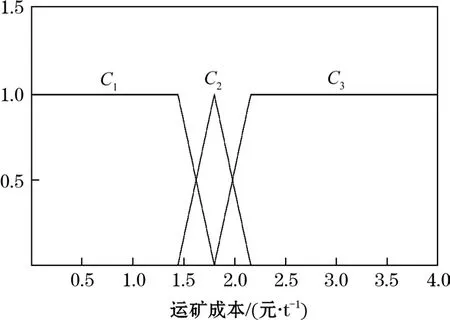
圖4 運礦成本單指標測度函數
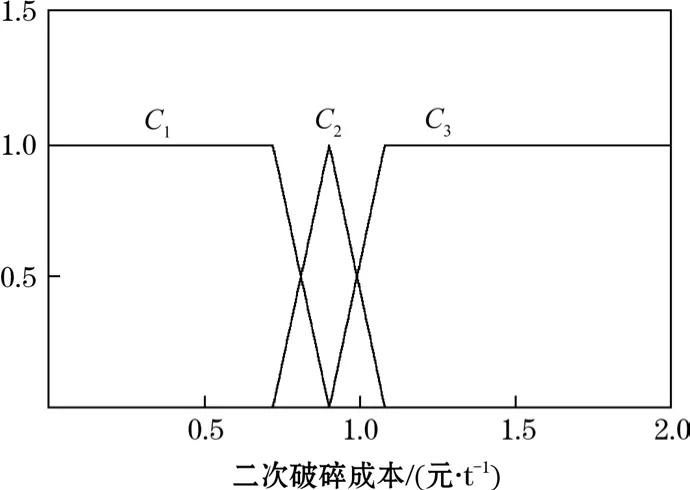
圖5 二次破碎成本單指標測度函數
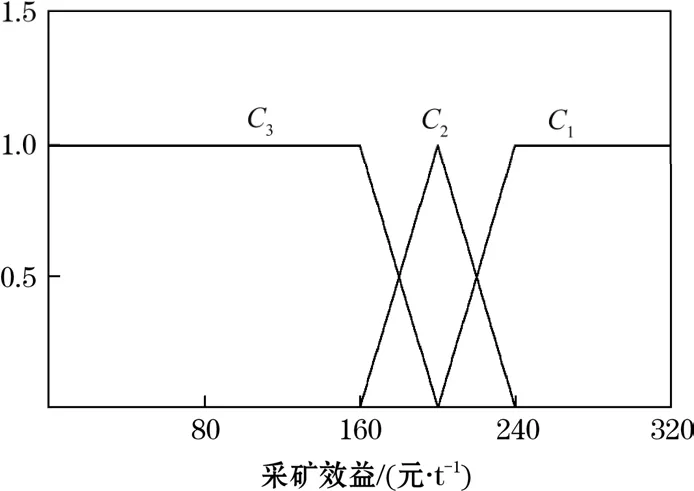
圖6 采礦效益單指標測度函數
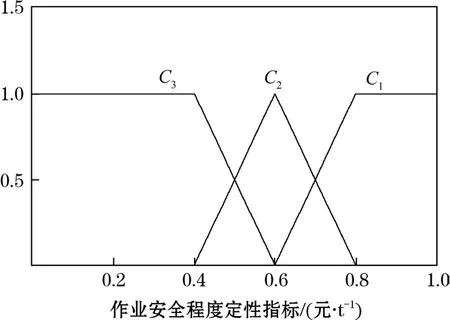
圖7 作業安全程度單指標測度函數
2 優選過程
2.1 單指標測度評價矩陣的建立
結合某鐵礦影響礦石合格塊度因素的實際情況,可得到某鐵礦中各指標的實測數據(見表2)。
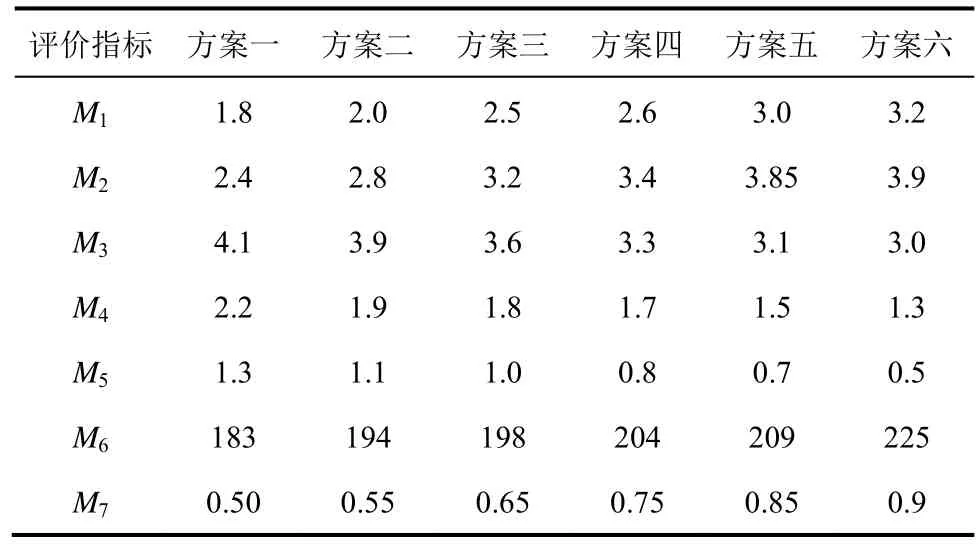
表2 各指標的實測數據
根據構造的單指標函數,可建立某鐵礦礦石合格塊度的單指標測度矩陣:
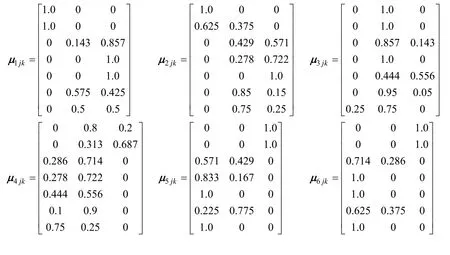
2.2 指標權重的確定
根據單指標測度矩陣以及熵權法確定指標權重的方法[10],M1的指標權重為:ω1={0.186, 0.186,0.116, 0.186, 0.186, 0.071, 0.069},用同樣的方法可以確定出其他各個指標的權重,在這里就不一一列出。
2.3 多指標綜合測度評價向量
根據多指標綜合測度評價向量公式[10],可以確定各個方案的多指標綜合測度評價向量為:{0.372,0.092, 0.536};{0.228, 0.306, 0.406};{0.023, 0.912,0.065};{0.249, 0.633, 0.118};{0.515, 0.121, 0.364};{0.611, 0.047, 0.342}。
2.4 評價等級的確定
結合某鐵礦現場實際情況,在本研究中,以方案一為例,根據多指標綜合測度向量{0.372, 0.092,0.536},C3(Ⅲ級)的權重0.536最高,因此,方案一的評價等級為Ⅲ級,同樣的,可以得到其他幾個方案的評價等級,其結果見表3。
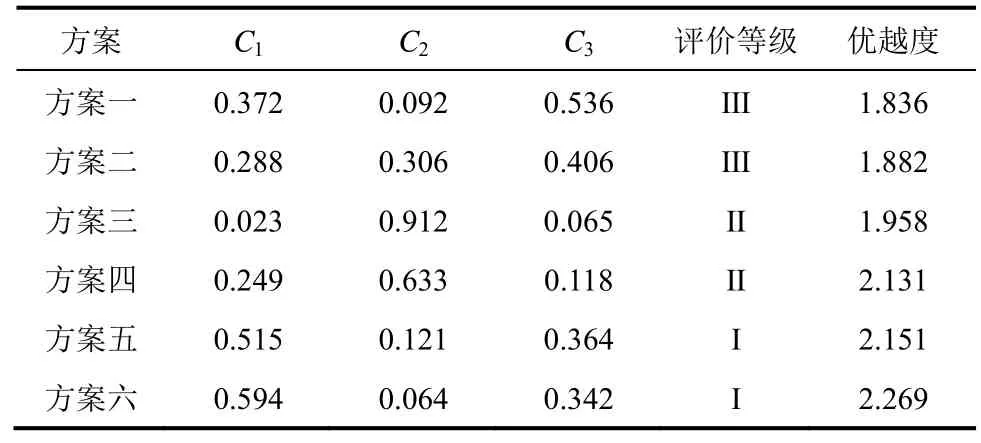
表3 各方案的評價等級及優越度
根據C1>C2>C3,可以得出方案一的優越度為:0.372×3+0.092×2+0.536=1.836,同理可以得出其他方案的優越度,其結果見表3,因此,可以得出各方案的優越度排序為:方案六>方案五>方案四>方案三>方案二>方案一,方案六是最優的。
2.5 模糊評判及對比分析
根據文獻[2]中的多目標模糊決策方法確定的評判結果為:Zj={0.6556, 0.6964, 0.7392, 0.7790,0.9162, 0.9590}。該方法采用的是專家咨詢權數法,綜合值Zj越大,方案的優越度就越高,因此方案的優越度排序為:方案六>方案五>方案四>方案三>方案二>方案一。
綜合兩種方法的結果,可以得出方案的優越度排序是一致的,因此采用未確知測度優選礦石合格塊度是可行的。
3 結論
(1)結果表明,某鐵礦礦石的最優合格塊度為 700 mm,這與礦山現場生產實際也較為吻合,由于礦石合格塊度變大,在一定程度上增加了礦山的投資,但給礦山帶來的安全效益和經濟效益也是巨大的,因此,采用未確知測度理論優選出來的某鐵礦礦石最優合格塊度是合理的。
(2)本研究中將熵權法應用于確定各評價指標的權重,可避免人為主觀因素的影響,其結果更加符合現場生產實際,具有快速、高效和精度高等優勢,可為礦山確定礦石合格塊度提供一種新的研究方法。
(3)本文采用未確知測度方法,利用熵的方法確定權重,建立了評價礦石合格塊度的模型,得出了最終的優選結果,豐富了礦山確定礦石合格塊度尺寸的評價方法,具有一定的應用意義。但是評價結果的好壞,很大程度取決于指標等級建立的好壞,因此確定礦石的合格塊度的評價方法還有待進一步研究。

