基于堿金屬磁力儀的銣原子橫向弛豫時間測量方法

岳亞洲，雷 興，曹耀輝，李 俊，劉元正，明澤額爾頓

（1.飛行器控制一體化技術國防科技重點實驗室，西安710065；2.西安飛行自動控制研究所，西安710065）

原子氣室是核磁共振陀螺核心器件。原子氣室內充有堿金屬原子蒸汽（常見為銣Rb）、淬滅及緩沖氣體氮氣（N2）、轉速敏感惰性氣體（129Xe和131Xe）[1-3]。Rb蒸汽作為原子極化轉移介質和惰性氣體拉莫爾進動信號檢測核心介質[4]，其極化率和弛豫時間直接決定了惰性氣體最終可達到的極化率以及陀螺共振信號的幅值[5-7]。尤其是弛豫時間的長短對評價氣室性能至關重要，一般而言，陀螺性能越高要求Rb原子的弛豫時間越長。

實際情況下，Rb原子弛豫時間增加與氣室尺寸減小之間存在矛盾。陀螺小型化要求氣室微型化，2014年美國諾格公司采用2 mm×2 mm×2 mm氣室在10 cm3陀螺整體封裝內實現導航級陀螺精度。該公司計劃在未來實現5 cm3的陀螺封裝[8]，要求的氣室尺寸更小。對于該微型氣室，銣原子與氣室壁之間碰撞對弛豫時間的影響更為顯著，需研究氣室內壁鍍膜技術以提升銣原子弛豫時間[9-11]。與此同時，研究氣室內銣原子弛豫時間的快速測量方案用于評價鍍膜方案優劣則顯得尤為重要。

銣原子極化弛豫時間從物理機制上講分為縱向弛豫時間T1和橫向弛豫時間T2，橫向弛豫干擾因素比縱向弛豫多，導致T1恒大于T2，T2對銣原子極化率以及陀螺性能影響更大，因此在研究時均將橫向弛豫時間T2作為氣室性能優劣的評判標準。

本文分析了現有測量方法優缺點，以核磁共振陀螺內稟銣原子磁力儀為基礎，提出一種測量銣原子橫向弛豫時間的工程化方法，利用仿真軟件對方案進行理論建模，最后設計實驗對三個不同充氣組分的氣室內堿金屬弛豫時間進行測量。

1 傳統的橫向弛豫時間測量方法

針對Rb原子橫向弛豫時間測量，傳統方法[12]包括自由感應衰減法、磁共振展寬擬合法和旋轉坐標系下的橫向磁矩分量比值擬合法，這三種方法均基于銣原子順磁共振原理。

如圖1所示，靜磁場B0以及抽運光沿z軸施加于核磁共振陀螺氣室，銣原子沿z軸極化，穩態極化磁矩用M0表示。在x軸施加激勵磁場Bx=B1cos （ω1t），利用旋轉波近似，在旋轉坐標系下將銣原子極化磁矩穩態結果描述如下：

圖1 原子順磁共振原理簡圖Fig.1 Schematic diagram of the atom paramagnetic resonance

式(1)中，T1，T2分別表示Rb原子的縱向及橫向弛豫時間，ωΔ 為激勵磁場頻率失諧量，γ為銣原子旋磁比。

[Mx' ,My' ,Mz']表示銣原子磁矩在旋轉坐標系［x',y',z'］軸上的投影，其在實驗室坐標系下投影為：

結合式(1)(2)將傳統三種測量方法基本原理描述如下：

自由感應衰減法原理是施加激勵磁場Bx=B1cos （ω1t），待系統穩定之后，關閉激勵磁場，此時檢測到的信號My隨時間的變化滿足：

對測量結果按式(3)擬合，提取其中的指數衰減項即可確定橫向弛豫時間T2。

磁共振展寬擬合法的原理是利用式(1)及(2)中Mz的表達式，可得Mz對激勵磁場頻率響應的半高寬為：

比值擬合法則選取式(1)中的Mx',My'的比值

測量時，先通過實驗測量固定z軸磁場B0下的共振頻率ω0。然后在ω0附近選擇一系列值。將測量所得的Mx分別用 cos（ωat）和 sin（ωat）解調后通過低通濾波器，確定Mx',My'及其比值，將上述比值以ωΔ 為自變量進行擬合，即可實現對T2的測量。

上述三種測量方法在實際操作過程中存在一些問題，自由感應衰減法的測量精度最高，需要施加的共振頻率較高（幾十到幾百kHz），Rb弛豫時間一般為微秒量級，關閉激勵磁場之后經過有限幾個振蕩周期，衰減信號衰減為零，擬合有效數據少，限制了測量精度。

磁共振擬合展寬法忽略了式(2)分母（ ΔωT2）2的影響，測量精度較低。

比值擬合法采用了調制解調的方法，該方法建立在由氣室及電路系統所導致的延時相對于激勵頻率可忽略的假設之上，然而在實際情況中并非如此。

在分析傳統測量方法優缺點的基礎上，本文基于堿金屬磁力儀測磁原理提出Rb原子橫向弛豫時間測量的新方法。

2 橫向弛豫時間測量新方法

極化Rb原子在磁場的運動可用布洛赫方程描述：

穩態情況下銣原子磁矩在空間三軸上的投影：

與式(1)相比，式(7)適用于低頻磁場（低于幾kHz），且未采用旋轉波近似，與實際情況的貼合度更高。

探測光沿y軸注入氣室時，探測光功率或偏振方向變化對應My的變化。

調整Bz使得：

此時My信號可簡化為：

以此為基礎，本文提出基于堿金屬磁力儀的銣原子橫向弛豫時間測量方法。

選擇固定的靜磁場B0，其具體值可通過氣室內惰性氣體核磁共振現象嚴格確定，測量誤差優于0.1 nT。利用橫向線圈組依次施加等值的Bx和By，針對My兩次測量的結果分別為：

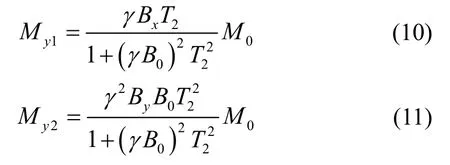
兩次測量結果的比值：

式(10)-(12)即為本文提出氣室內銣原子橫向弛豫時間測量的基本理論。與傳統的比值擬合法相比，無需進行解調以及時序對準，理論上測量精度更高。

3 理論建模

基于上述理論分析，利用數學仿真軟件搭建銣原子橫向弛豫時間測量的仿真模型。

如圖2所示，Bx，By，Bz為人為施加磁場，Bz取核磁共振陀螺工作典型值10μT，r_Rb表征銣原子旋磁比為2π×6996Hz/μT。T2為銣原子橫向弛豫時間。為了避免實際情況中空間雜散磁場的影響，Bx，By輸入信號為100Hz的交流信號，峰峰值為20nT，如圖3所示。

圖2 銣原子橫向弛豫時間測量方案仿真模型Fig.2 Simulation model of rubidium transverse relaxation time measurement method

圖3 仿真模型中X或Y軸輸入交流磁場信號Fig.3 X or Y input ac magnetic field signal

按上節所述的測量流程進行仿真：

① 設定T2=10 μs，T1=2T2，Bx=10nTcos（2π×100t），By=0，檢測My輸出交流信號峰峰值sig1；

② Bx=0，By=10nT×cos(2π×100t)，檢測My交流信號峰峰值sig2；

③ 利用式(10)，求解弛豫時間T2；

④ 改變T2令其分別為20μs，40μs，T1保持為T2的兩倍，重復步驟①～③，分別計算不同T2時刻的仿真結果。

仿真結果如下，以T2=10μs，T1=2T2為例，兩次測量的My輸出如圖4、5所示，仿真輸出結果與仿真時y軸磁矩與銣原子沿y軸完全極化時磁矩的比值，量綱為1。

圖4 Bx =10nTcos（ 2π × 1 00t ）, By = 0時My信號Fig.4 My output when Bx =10nTcos（2π × 1 00t ）, By =0,

圖5 Bx = 0, B y = 10nTcos（ 2π × 1 00t ）時My信號Fig.5 My output when Bx = 0, By = 10nTcos（ 2π × 100t ）

兩次測量信號輸出峰峰值分別為2.162×10-4和9.5008×10-4，計算相應的2,meas T =10.0002 μs；仿真輸入 T2分別為 20 μs，40 μs時， T2,meas則分別為19.9927 μs，39.9897 μs，測量誤差小于0.4‰。

為比較本測量方法與傳統方法，搭建自由感應衰減測量方案仿真模型，如圖6所示。仿真條件：施加z軸磁場10 μT，x軸激勵磁場頻率69.98 kHz，橫向弛豫時間設定為10 μs。仿真開始階段，持續激勵0.05 s后關閉激勵磁場，利用模擬示波器記錄My衰減輸出。

圖6 自由感應衰減測量方案仿真模型Fig.6 Simulation model of free induction decay measurement method

如圖7所示，My振蕩1～2個周期之后迅速衰減為0，無法進行擬合進而求解T2。為解決該問題，將z軸磁場提升至50 μT，與此對應，激勵磁場頻率須提升至349 kHz，My在衰減為零之前約有5～10個振蕩周期，如圖8所示，基本滿足擬合數據量的需求，測量所得的T2,meas為10.001 μs（ δ= 0.017μs ，誤差為1.7‰），精度比本文提出的方法低。要提升該方法精度，應繼續提升靜態磁場以及x軸激勵磁場頻率，但這樣就需要系統有更好的響應度和采樣速率，在實際工程測量中并不可取。

圖7 T2=10 μs，振蕩磁場頻率69.8 kHz自由感應衰減Fig.7 Free induction decay when T2=10 μs and excitation magnetic field frequency is 69.8 kHz

圖8 T2=10 μs，振蕩磁場頻率349 kHz自由感應衰減Fig.8 Free induction decay when T2=10 μs and excitation magnetic field frequency is 349 kHz

4 實驗測量

實驗中選用三支4 mm×4 mm×4 mm氣室，分別標號1，2，3，除Rb原子外，1號氣室充入70 torr的N2和5 torr的自然豐度的Xe。2號氣室充入100 torr的N2和5 torr的自然豐度的Xe。3號氣室充入500 torr的N2和5 torr的自然豐度的Xe。實驗裝置如圖9所示，整個氣室處于磁屏蔽系統[13]中，得益于屏蔽系統，氣室附近剩磁低于10 nT。氣室加熱由無磁電加熱系統提供，溫度穩定性優于0.01 °C。

圖9 銣原子橫向弛豫時間測量裝置Fig.9 Measuring device for rubidium transverse relaxation time

z軸磁場由改進型螺線管產生，通過氣室內129Xe核磁共振實現磁場值的精確控制；x、y軸磁場由亥姆霍茲線圈產生，兩個磁場線圈通過精密設計保證其標度因子差值不超過1‰。x，y軸磁場信號由信號源給出，輸出阻抗50歐，頻率100 Hz，幅值100 mV。選擇交流磁場信號的原因是為了抑制氣室環境中雜散直流磁場的影響。

抽運光和探測光由分布式反饋激光器（DFB）產生，抽運光為波長795 nm的圓偏振光，為抑制抽運光頻率波動對測量結果的影響[14]，采用外置飽和吸收光路對抽運光進行穩頻。探測光為波長780 nm的線偏振光。抽運光沿z軸方向進入氣室，探測光經玻片、起偏器以及反射鏡之后沿y軸注入氣室。探測光經氣室之后被差分探測系統接收輸出無直流的交流信號，交流信號峰峰值對應磁力儀對100 mV橫向磁場的響應。

通過變化氣室內129Xe共振頻率確定5個靜態磁場B0，分別為20.37 μT、16.98 μT、13.58 μT、10.18 μT和6.79 μT。

按照第2節中描述的測量流程，逐次施加Bx，By交流信號，在不同B0情況下所得結果如表1-3所示。

表1 不同B0下1號氣室銣原子橫向弛豫時間測量結果Tab.1 Measure results of transverse relaxation time of no.1 cell under different static magnetic fields

表2 不同B0下2號氣室銣原子橫向弛豫時間測量結果Tab.2 Measure results of transverse relaxation time of no.2 cell under different static magnetic fields

表3 不同B0下3號氣室銣原子橫向弛豫時間測量結果Tab.3 Measure results of transverse relaxation time of no.3 cell under different static magnetic fields

以表2中Sig2/Sig1為縱坐標，B0為橫坐標，作圖如圖10所示。

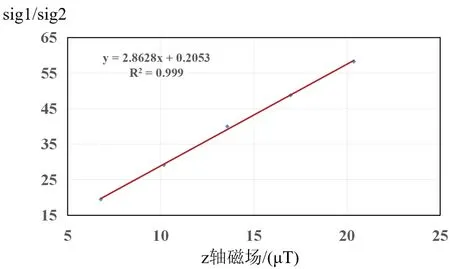
圖10 2號氣室內，Sig2/Sig1與z軸磁場關系Fig.10 Relation between Sig2/Sig1 with z-axis magnetic fieldin no.2 cell

對圖10線性擬合，可知γBzT2= 2.8996，反推T2為65.9 μs。為驗證測量結果準確性，利用自由感應衰減法對氣室弛豫時間進行了再次測量。選定B0=20.36 μT，激勵磁場頻率為142 KHz，銣原子共振信號衰減到e-1時約有10個振蕩周期，如圖11所示，滿足式(3)擬合數據量的需求，擬合結果T2,meas=67 μs,與本文提出的方法測量結果一致，印證了本方案測量結果的有效性。

圖11 自由感應衰減法測量2號氣室銣原子弛豫時間Fig.11 Measure results of free induction decay method in no.2 cell

5 分析與討論

氣室中堿金屬橫向弛豫時間受溫度、抽運光/探測光光束質量以及磁場梯度等因素的影響。本文主要討論其在核磁共振陀螺環境下的測量方法。

在理論仿真模型中，改變不同橫向弛豫時間T2輸入值，本方案測量結果與設計預設值區別小于0.4‰，在理論上驗證了方法的正確性。

在實驗驗證時，選擇三支充氣參數不同氣室進行橫向弛豫時間測量，結果顯示，氣室內N2分壓為100 torr時，銣原子橫向弛豫時間最長，當氮氣氣壓減小或者增大時，弛豫時間均有降低的趨勢，該結果與2013年 Ricardo Jimenez Martinez給出的4 mm×4 mm×4 mm氣室內，氮氣最優分壓約為120 torr的結果一致[15]。改變z軸磁場幅值，分5次進行了橫向弛豫時間測量，測量誤差分別為4.6‰，5.2‰，6.8‰。為驗證測量結果準確性，利用自由感應衰減法對2號氣室的橫向弛豫時間再次進行測量，結果基本一致（67 μsVs.65.3 μs），但存在2.5%的區別。可能原因為x、y軸線圈之間存在串擾，實驗要求Bx=0以及By=0的兩輪試驗沒有嚴格保證。利用磁通門計對線圈之間串擾進行標定，線圈之間的串擾約1.2%，將串擾修正之后，本方案的測量的弛豫時間為67.2 μs，與自由感應衰減法結果誤差為2.9‰，縮小了一個數量級。

通過理論仿真以及實驗驗證，本文提出的橫向弛豫測量方案操作簡單，準確度高。與自由感應衰減法相比，無需高激勵磁場頻率以及z軸靜態磁場，尤其在弛豫時間低于10 μs的氣室狀態下測量準確度更高，操作更為簡單，且避免了由于擬合對測量帶來的不確定性。

6 結 論

本文在分析現有銣原子橫向弛豫時間測量方案的基礎上，提出基于銣原子磁力儀的橫向弛豫測量方案，操作方式更為簡單，易于工程實現。搭建數理模型進行仿真驗證，測量誤差小于0.4‰。利用本方案對三支充氣參數不同的氣室實際測量，組間誤差小于6.8‰，通過仿真模型以及實驗測量，驗證了方案的可行性，測量數據的穩定性達4.6‰。在與自由感應衰減法的比較實驗中，本方案與自由感應衰減法差別不超過5%，驗證了測量數據結果的準確性。

理論仿真以及對比實驗結果均表明，本方案可有效進行氣室內銣原子橫向弛豫時間測量，測量結果準確。隨后的工作擬對實驗裝置中x、y軸線圈進行優化，進一步降低其耦合，實現測量精度的進一步提升。