半球諧振子裝配傾角誤差對頻率裂解的影響分析

寧友歡，伊國興，奚伯齊，解偉男，魏振楠，王常虹

(哈爾濱工業大學航天學院，空間控制與慣性技術研究中心，哈爾濱 150080)

半球諧振陀螺是一種全固態振動陀螺儀，具有精度高、體積小、可靠性高、功耗低、啟動時間短等特點。目前高精度的半球諧振陀螺具有0.0001 °/h的高精度，長達20年的使用壽命，可達0.995的高可靠性[1]。由于高精度、高可靠、結構簡單，極具體積、質量等綜合優勢，在深空探測、衛星穩定控制、航天器導航、石油鉆探、航海等領域具有廣闊的應用前景[1-5]。

國內外針對半球諧振子頻率裂解的形成演化機理以及調頻和測試方法進行了大量的研究，但這些研究主要集中在諧振子加工誤差及材料各向異性對頻率裂解的影響方面[6-13]，針對裝配誤差造成頻率裂解的影響機理研究較少。霍炎等人針對質量分布不均勻對諧振子頻率裂解以及質量缺陷對振動諧振子駐波漂移的影響進行了研究[7]。文獻[8]推導了具有質量缺陷的半球形殼體的分頻解析模型，并建立了一個預測不完美諧振腔微調質量的函數。在頻率裂解修調方面，文獻[9]研究了一種化學刻蝕方法來消除導致頻率裂解的半球形諧振子質量不均勻性的第四次諧波，該方法可以將半球諧振子的頻率裂解降低到0.05 Hz。胡曉東等人利用離子束去除半球形諧振器質量缺陷的第1-4次諧波，該方法能將半球諧振子的頻率裂解從0.46 Hz減少到0.004 Hz[10,11]。針對頻率裂解的測試，李紹良等提出了基于幅頻響應特性的半球諧振子頻率裂解與固有剛度軸方位角測定方法[12]。俄羅斯馬特維耶夫提出了基于幅相頻特性描繪法的固有剛度軸方位角和頻率裂解的確定方法[13]，為半球諧振陀螺儀的研究奠定了理論分析基礎。裝配過程中的裝配誤差產生應力、剛度分布不均勻，會對諧振子頻率裂解、品質因數等性能產生影響，文獻[14]針對裝配誤差對諧振子品質因數的影響進行了分析，并對減小裝配誤差的解決方案進行了研究。文獻[15]針對非理想軸對稱殼體諧振器的頻率裂解的產生進行了分析，基于軸對稱多曲面殼體結構的諧振器，提出了一種消除頻率分裂的方法，并驗證了所述方法的有效性。

本文針對半球諧振子振動性能受裝配誤差的影響展開研究，重點研究了裝配過程中產生的傾斜誤差對半球諧振子頻率裂解的影響機理。首先基于半球諧振陀螺電容式驅動原理，將半球諧振子唇沿與平板電極等效為平板電容器，建立等效電容與裝配誤差之間的數學模型；然后根據等效電容兩端電壓與半球諧振子靜電力之間的數學模型，分析靜電力不均勻對諧振子剛度的影響；最后，建立剛度擾動對頻率裂解的影響機理模型，分析傾角誤差對諧振子頻率裂解的影響演化機理。

1 裝配誤差對頻率裂解形成機理分析

1.1 半球諧振子頻率裂解形成理論分析

半球諧振子的固有頻率不僅受材料性能的影響，而且與其幾何參數有關，完美的諧振子不會產生頻率裂解。然而，材料的各向異性和諧振子制造工藝等誤差的四次諧波會導致諧振子中出現兩個相互成45 °夾角的固有剛性軸。

如圖1所示為半球諧振子二階振動等效模型，黑色的圓為諧振子環形模型的外邊緣，紅色和藍色分別是兩個振動模態的振動圖，兩個模態形成互相間隔45 °的兩個固有軸。半球諧振子在振動時，沿這兩個軸中每一個軸的振動固有頻率都能達到極大值和極小值，為了便于描述，一般將固有頻率較小的軸稱為“重軸”，固有頻率較大的稱為“輕軸”。振動圓頻率的極大值和極小值的頻率差稱為固有頻率的裂解，頻率裂解定義為：

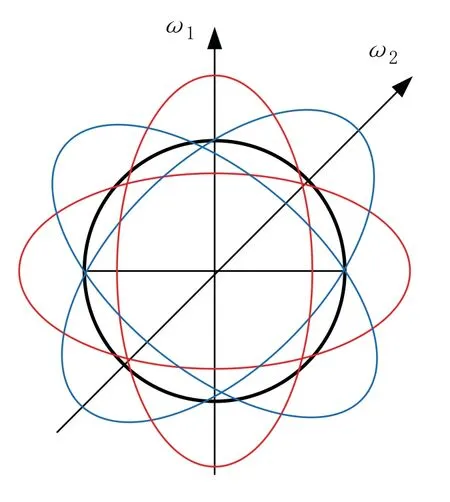
圖1 諧振子二階振動等效模型Fig.1 Second-order vibration equivalent model of resonator

對具有頻率裂解的諧振子振動信號進行采集，諧振子振動信號的幅頻響應分析曲線如圖2所示。

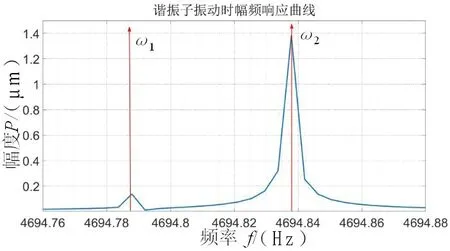
圖2 半球諧振子頻率裂解信號Fig.2 Hemispherical resonator frequency split signal

當所受激振力的方位角與固有剛性軸不重合時，半球諧振子兩個剛性軸處的振動模態會被不同程度激勵起。振動信號出現了兩個信號峰值，分別對應諧振子剛性軸的兩個振動模態，信號峰對應的頻率即為振型的諧振頻率，兩個峰的不同幅值反映了激振力方位與固有剛性軸方位的偏差。

由于材料缺陷及加工誤差導致兩個節點和兩個波腹組成的兩種工作模式之間出現頻率差。這種缺陷導致陀螺效應的損失，甚至不能檢測角運動。因此，頻率裂解的存在不僅能引起駐波漂移，產生機械耦合誤差，還會降低半球諧振陀螺的靈敏度。頻率裂解是造成半球諧振陀螺零偏誤差的主要原因之一，頻率裂解的形成機理研究是提高半球諧振陀螺儀測量精度的關鍵技術。

1.2 半球諧振子裝配傾角誤差與等效電容的模型

半球諧振子與平板電極基座的裝配通常采用粘合劑將二者固連，在表頭裝配過程中，由于設備、夾具等方面的原因，導致諧振子在裝配過程中產生了偏心、傾斜等裝配誤差，直接影響諧振子與平板電極初始的間距不均勻，從而導致諧振子的振動在正交軸分解時產生誤差。同時，裝配誤差也會影響靜電力的分布，改變了剛度分布的均勻性。半球諧振子裝配傾角誤差如圖3和圖4所示。

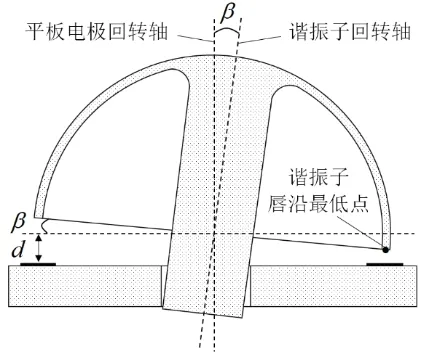
圖3 安裝傾角誤差示意圖Fig.3 Schematic diagram of installation inclination error

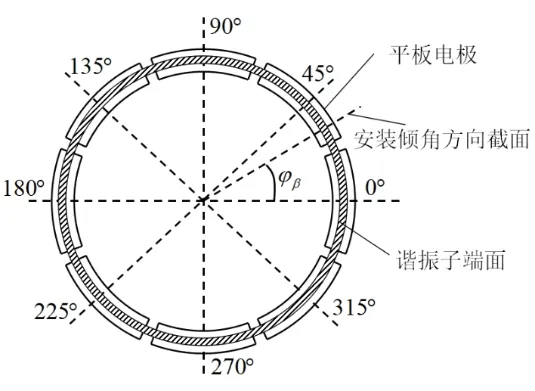
圖4 安裝傾斜方位角示意圖Fig.4 Schematic diagram of installation tilt azimuth

由于裝配傾角誤差的存在，裝配后半球諧振子振動受靜電力的影響，導致剛度分布不均勻，從而對諧振子頻率裂解產生影響。半球諧振子唇沿與平板電極形成等效電容，電容值由諧振子唇沿與平板電極的正對投影面積以及兩者之間的距離決定。由于受到裝配工藝的限制，諧振子與電極基座裝配過程中，諧振子回轉軸與平板電極回轉軸將不可避免的產生大小為β的安裝傾角，由此造成諧振子唇沿與平板電極間周向各點的間隙不同。假設其平均間距為d，其中間距最小處對應諧振子唇沿最低點，如圖3所示。連接諧振子回轉中心與諧振子唇沿最低點所得直線在平板電極表面的投影與0 °電極軸線方向存在角βφ，稱為安裝傾斜方位角，如圖4所示。若沿著圖4中通過回轉軸與0 °電極軸線的切割平面將諧振子及平板電極向周向方向展開，則可得到如圖5所示諧振子周向展開圖。

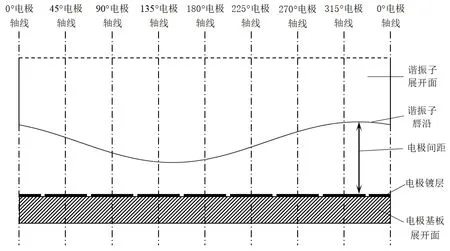
圖5 諧振子周向展開圖Fig.5 Circumferential development diagram of harmonic oscillator

由圖5分析可知，各激勵及檢測電容間距在安裝傾角及傾斜方位角的作用下呈正弦規律變化，通過對該規律的解析，可以根據測量得到的各靜態電容值獲取安裝傾角和安裝傾角方位。

如圖6所示的平板電極及其等效示意圖，電極均勻分布在基板表面，在空間中處于同一平面，各電極周向邊界通常設計為互相平行。基于此，為了便于分析，引入“等效間距角”的概念對各電容的分布進行建模[5]。根據對檢測電容幾何結構的分析可得到等效電容的周向邊界，其徑向邊界則由諧振子內表面半徑1r及諧振子外表面半徑2r決定。

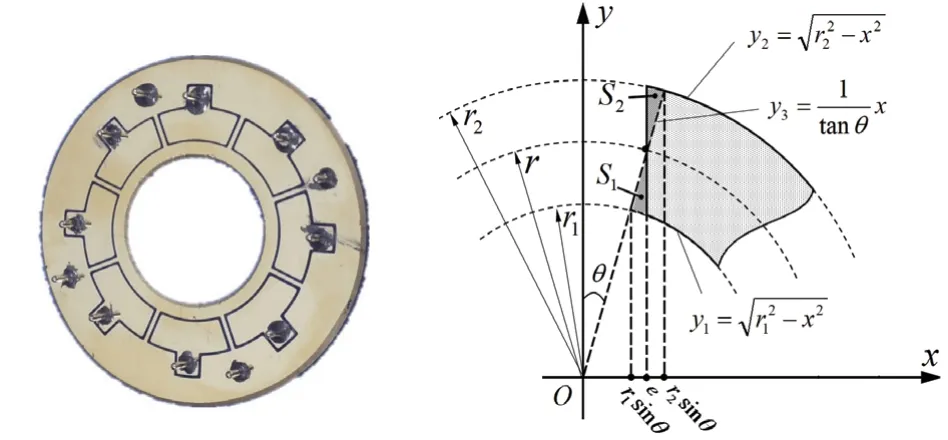
圖6 平板電極及其等效示意圖Fig.6 Schematic diagram of plate electrode and its equivalent

圖6中實線包圍區域為實際的激勵或檢測電容區域，各電極間由寬為2e的電氣間隙隔離。為便于電容積分計算，假設各電極由中心角為2θ的扇形區域分割，稱其為等效間距角。當圖6中陰影區域S1與S2面積相同時，利用電氣間隙隔離2e及等效間距角2θ計算得到的電容值相同。θ可由式(2)計算得到。

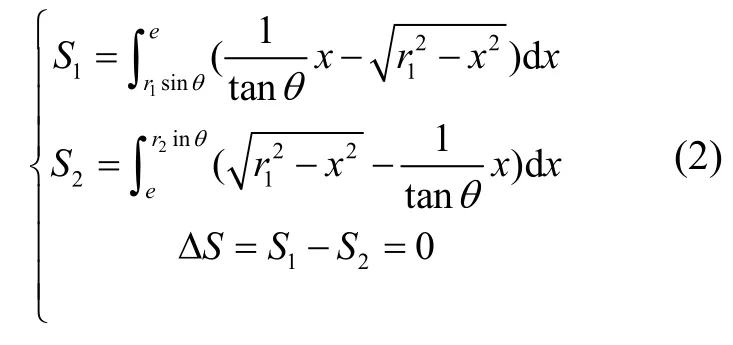
電極的邊界可利用周向方向的角度表示：

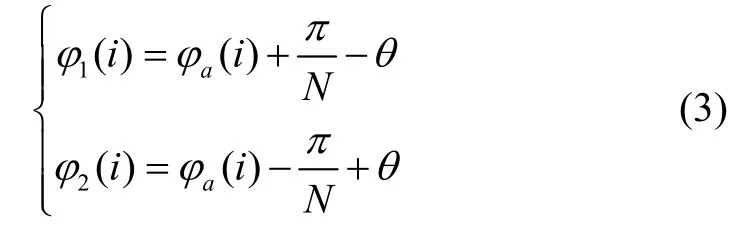
式(3)中，φ1(i)、φ2(i)為第i個電極的周向邊界；φa(i)為第i個電極的軸線角度，如對于第一個電極（0°電極）有φa(1) = 0°；N=8為電極的數量。

當半球諧振子振動時，唇沿表面與平板電極之間的間隙可以表示為：

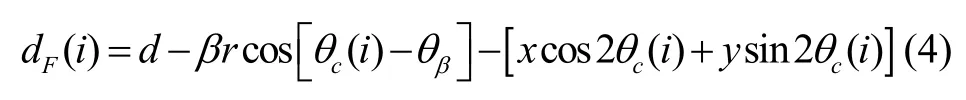
則根據平行板電容器原理，忽略諧振子端面的扭轉形變，可得第i個電極的靜態容值[5]CF(i)：

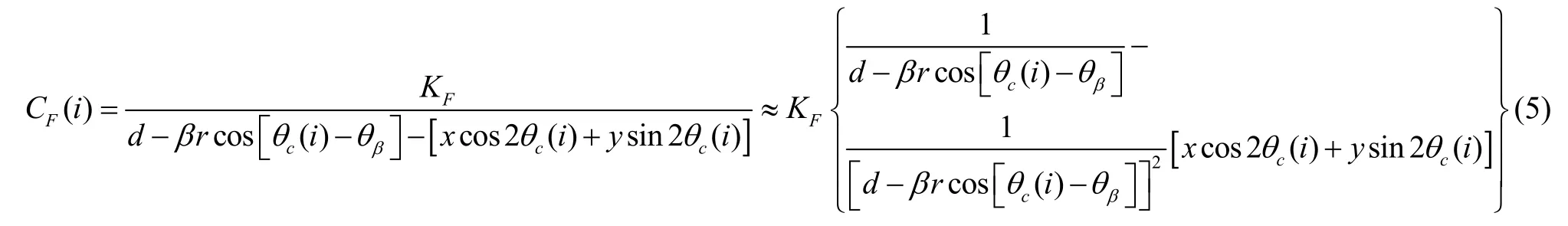
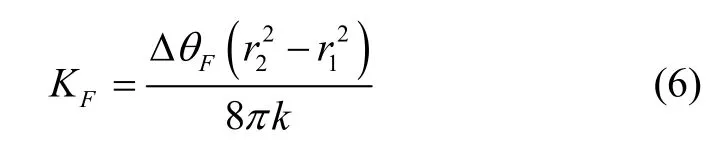
其中：k為靜電常數，k= 9.0×1 09N· m2/C2；β為以 0 °電極軸線為起始位置的圓周角；△θF=θi(r) -θi(l)表示平板電極上第i個電極所占位置角度。

1.3 半球諧振子激勵模型

半球諧振陀螺采用電容式驅動，半球諧振子唇沿與平板電極之間形成等效平板電容器。因此，根據拉格朗日力學原理，諧振子唇沿與平板電極之間的靜電力為：

其中，Ec為存儲的電勢能，

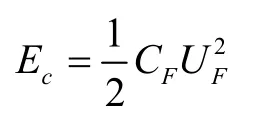
UF為在電容兩端施加的電壓。

對于第i個電容器，當諧振子振動時，對靜電力進行簡化后其表達式為：

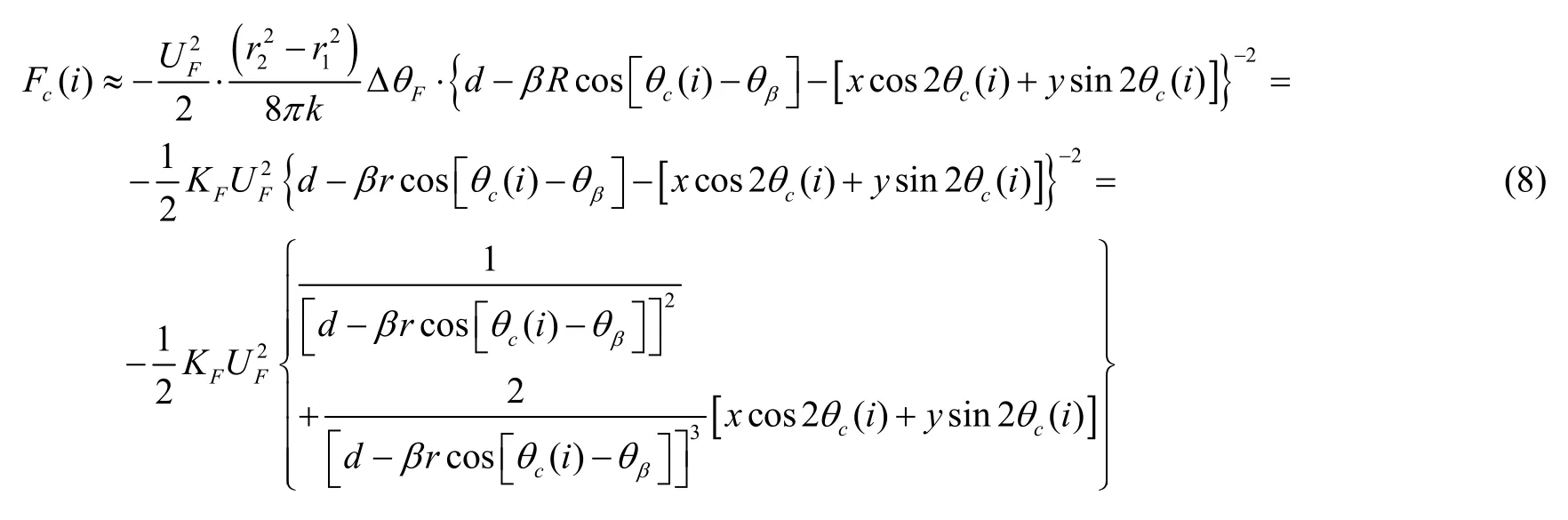
由于傾斜導致的誤差可以表示為：

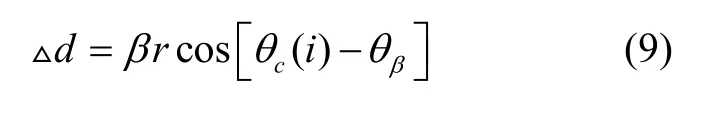
則靜電驅動力可以表示為：

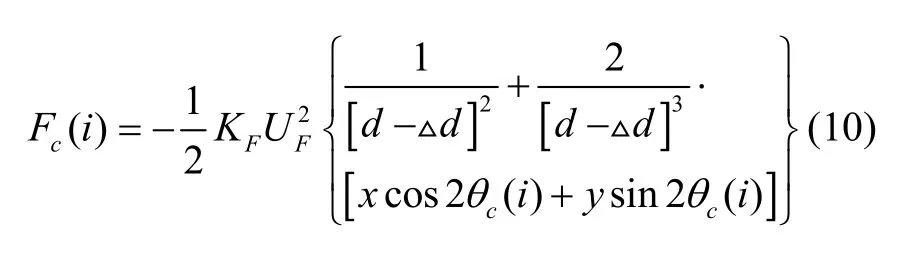
在實際裝配過程中，裝配誤差可以控制到很小的范圍，即：d?Δd，對靜電力進行泰勒局部展開，忽略高次項，保留低次項后可得：

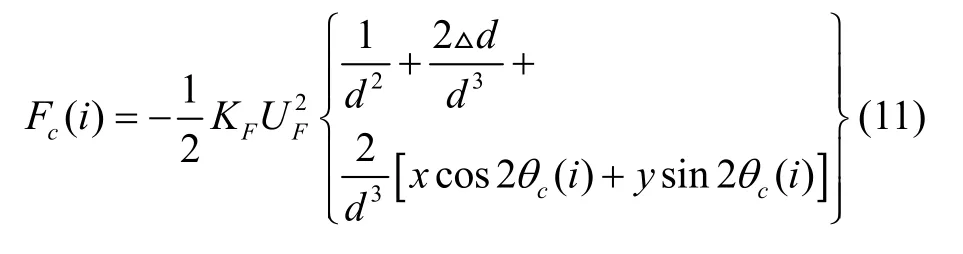
分析式(11)可知，靜電驅動力的第二項與傾斜誤差有關，由于該力的存在會影響諧振子的剛度系數，傾斜誤差的存在導致的剛度變化表示為：

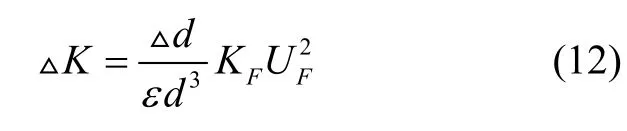
在剛度擾動的情況下諧振子頻率裂解可寫為:

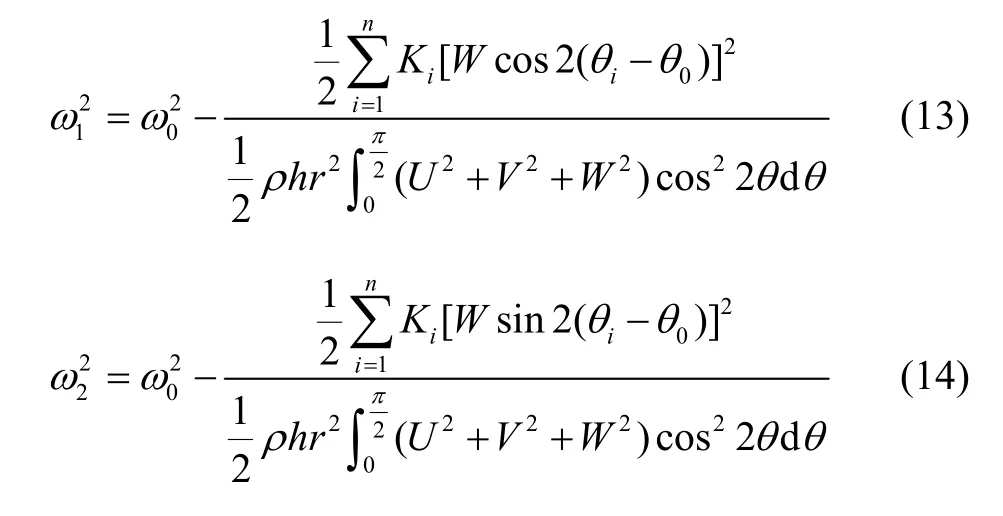
其中Ki表示離散后分析的第i個不平衡剛度大小，θi表示不平衡剛度的方位。

將式(13)(14)帶入式(1)中，化簡后即可確定裝配傾角誤差對半球諧振子頻率裂解影響的數學模型。

2 仿真及結果分析

基于等效電容與裝配誤差之間的數學模型，選取0 °位置的電極為參考，通過數值仿真分析軟件對不同安裝誤差狀況下靜態電容值的變化規律進行仿真，仿真參數如表1所示，仿真結果如圖8所示。

表1 模型仿真參數Tab.1 Type simulation parameters

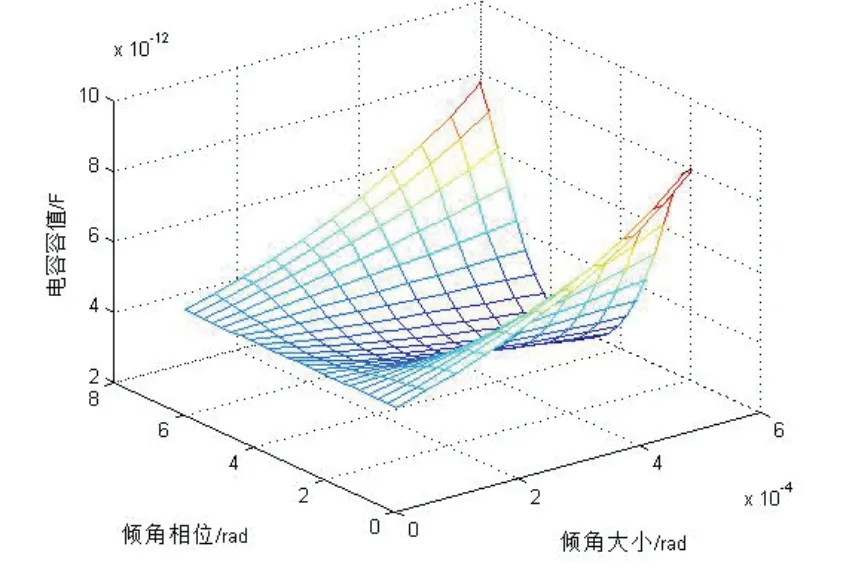
圖8 電容安裝誤差靜態模型Fig.8 Static model of capacitor installation error

由圖8的仿真結果分析可知：隨著安裝傾角的增加，電容容值偏離平均值的程度也逐漸增大，而在同一傾角大小下，電容值偏離平均值的程度由傾角相位決定。電容容值的變化由傾角大小的增加和傾角相位共同確定，即裝配傾角誤差可以由電容值的變化唯一確定。

基于等效電容模型，等效電容值由諧振子唇沿與平板電極的正對投影面積以及兩者之間的距離決定。通過電容的微小變化，等效半球諧振子的振動。由于傾角誤差導致等效電容的變化而形成的靜電力分布不均勻造成剛度擾動的數學模型，如式(11)所示，取理想條件下半球諧振子受到靜電力激勵時的剛度為參考，假設參考值為0，由傾角誤差引起的諧振子剛度擾動偏離平均值的誤差仿真結果如圖9所示。

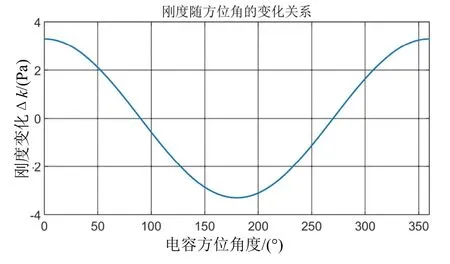
圖9 剛度隨方位角變化關系Fig.9 The relationship between stiffness and azimuth

由圖9分析可知，諧振子與電極基座裝配過程中產生的傾角誤差導致等效電容兩端的靜電力在安裝傾角及傾角方位角的作用下呈正弦規律變化。即安裝過程中形成的傾角誤差將會影響每一個電容的變化，進而在周向各點上產生了靜電力分布不均勻，其中間距最小處的靜電力較大，對剛度的影響也較大。剛度擾動引起頻率裂解的數學模型如式(12)-(14)所示，為進一步分析量化其影響規律，采用數值仿真分析軟件對該數學模型進行仿真分析，分析結果如圖10所示。

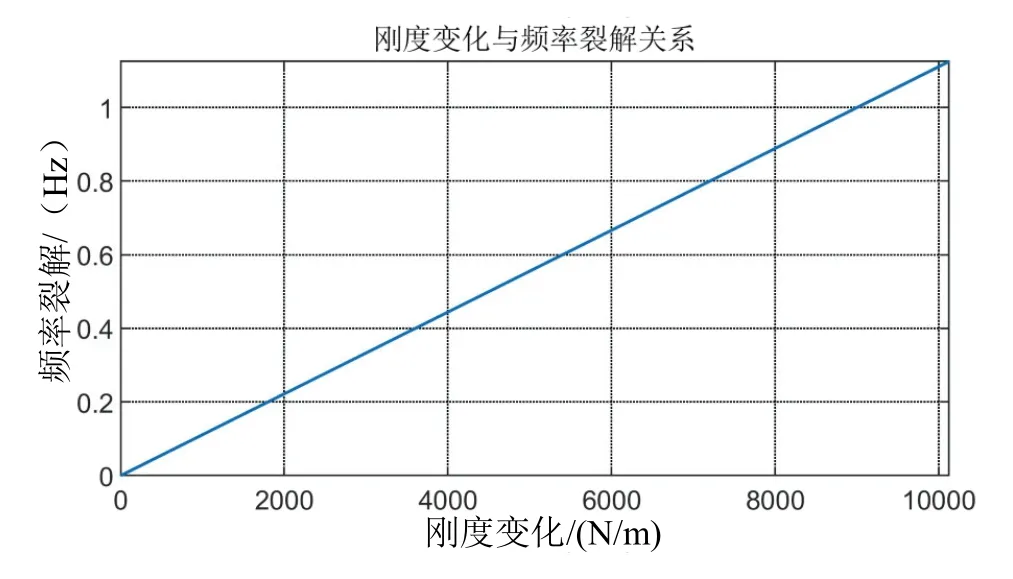
圖10 剛度變化與頻率裂解的關系Fig 10 The relationship between stiffness change and frequency cracking

由圖10的仿真結果分析可知，頻率裂解與剛度不均勻變化量呈正比關系。以直徑為30 mm的石英半球諧振子為例，當其剛度變化0.05%時，剛度缺陷所引起的頻率裂解約為1 Hz。

基于上述的分析，當石英半球諧振子與基座的裝配傾角誤差為1角秒時，頻率裂解為10-6Hz量級，而當裝配誤差增大到60角秒時，頻率裂解將達到10-4Hz量級。因此，根據半球諧振子應用需求，實際裝配過程中，為將裝配誤差造成的頻率裂解控制在10-4Hz量級以下，裝配傾角誤差應控制在1角分范圍以內。

3 結 論

本文圍繞半球諧振子裝配過程中產生的偏心、傾斜等誤差對頻率裂解的影響展開研究，建立裝配誤差對頻率裂解的影響機理模型，首先分析了傾角誤差對半球諧振子靜電力分布不均勻的影響，建立由于剛度擾動導致頻率裂解的數學模型，給出了安裝傾角誤差對頻率裂解的演化機理。以30 mm熔融石英半球諧振子為例進行誤差機理模型的仿真驗證，結果表明，諧振子與基座的裝配傾角誤差為1'時，由安裝傾角誤差引入的頻率裂解為10-4Hz量級。裝配誤差不僅會影響頻率裂解，也會影響諧振子品質因數、阻尼分布均勻性等性能指標，從而導致駐波漂移，影響半球諧振陀螺的精度。因此，對裝配誤差進行深入細致的研究，對優化裝配工藝，提高半球諧振陀螺儀性能有著重要的意義。