基于沉降實測數據的軟土地基土工參數優化計算*

劉展瑞，張潭，羅克文，呂琰，易真

(1.廣西壯族自治區玉林公路發展中心，廣西 玉林 537000；2.長沙理工大學 交通運輸工程學院，湖南 長沙 410114)

軟土地基具有高壓縮性與低承載力的工程特性，在上面修筑公路路堤會出現失穩和不均勻沉降，需對其進行加固處理。針對地基的固結排水過程，陳偉通過數值仿真計算，分析了堤基固結沉降過程及規律，并與現場水庫堤基的沉降監測數據對比，預測了堤基沉降達到穩定時所需的固結時間及最終固結沉降值。李強等介紹了雙曲線法、星野法、指數曲線法等沉降分析方法，并利用實測沉降數據推算了任意時間的沉降量，預測了軟土路基的沉降變形趨勢。周舟等結合嘉紹(嘉興—紹興)高速公路，分析了軟基沉降預測原理，提出了任意地基一維固結問題的解，并利用實際沉降數據對計算模型和參數進行反演，對公路最終沉降及工后沉降進行了預測。彭占淇從軟基的孔隙變化規律出發，以大應變固結理論為基礎建立適合軟土的三維固結模型，運用有限差分法構造顯示差分格式，并利用MATLAB軟件編程進行求解。謝康和對雙層地基一維固結特性進行分析，對荷載在時間任意變化及起始孔壓沿深度任意分布的情況下雙層地基一維固結進行了解答。但對基于現場沉降數據反算土工參數的研究沒有涉及。該文以廣西玉林市博白縣省道S209線路面大修工程軟基為原型施加荷載，使大部分沉降在預壓過程中完成，通過現場實測沉降數據計算得到各土層的土工參數。

1 多層軟土地基固結排水過程的理論推導

令cvi為成層土層的豎向固結系數，ui為時空狀態(成層土層i中任意一點任意時刻)下超靜孔壓力，H為n層地基總厚度，hi為第i層成層土厚度，mvi為土層i的體積壓縮系數，kvi為土層i的滲透系數，Esi為土層i的壓縮模量。其他參數定義如下：

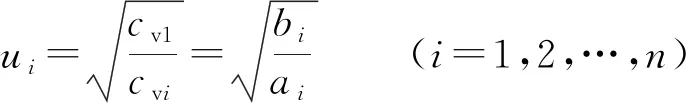
根據太沙基經典一維固結理論中超靜孔壓解的形式，ui可由下式表示：

(i=1,2,…,n)

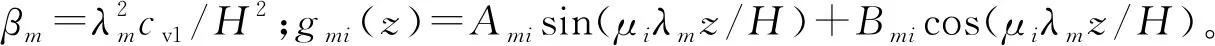
土層i的平均固結度為：

地基平均固結度為：

由于上述求解過程已求得任意成層土層i的平均固結度Ui，通過按沉降定義的地基平均固結度的計算公式即可計算出軟土地基的地基平均固結度。

2 多層軟土地基的軟化模型問題

基于現場實測數據，先通過最小二乘法推導成層地基在變荷載下任意層任意時刻的固結系數，即時空狀態下固結系數。太沙基經典一維固結理論雖被廣泛應用于工程建設項目中，但其假設與工程實際有很大差別，它將任何地基都視為一層，其計算結果可能與實際有所偏差。故在討論多層軟土地基固結排水過程時，考慮與固結系數關系非常大的時間及空間因素，推導出多層軟土地基的固結排水過程，計算任意時間點及成層地基的固結系數，該時空狀態下的固結系數能更好地為工程建設提供幫助。

玉林市公路片石處理為2層地基。針對雙層軟土地基，根據文獻[7]可得到a1、a2、b1、b2、cv1、cv26個主要土工參數滿足下式：

(j=1,2,…,ε)

即:

(1)

式中：Uij按式(2)計算。

(2)

式中：Cm按式(3)計算。

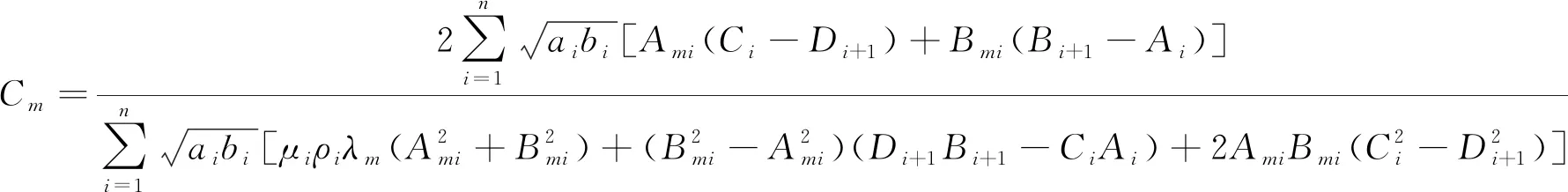
(3)

令：

(4)

令x=(x1,…,xn,xn+1,…,x2n,x2n+1,…,x3n)=(a1,…,an,b1,…,bn,cv1,…,cvn)，得：

(j=1,2,…,ε)

(5)

式(4)可轉化為：

(6)

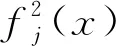
φj(x)=fj(xk)+?fj(xk)(x-xk)=

?fj(xk)T8x-[?fj(xk)Txk-fj(xk)]

(j=1,2,…,ε)

(7)

式(7)中右端為上述函數xk+1在xk點展開的一階泰勒多項式。令：

(8)

以式(8)中φ(x)近似替代F(x)，將φ(x)的極小值作為目標函數F(x)極小值的估計值，得：

φ(x)=(Ax-B)T(Ax-B)=

xTATAx-2BTAx+BTB

(9)

式中：A、B分別見式(10)、式(11)。

(10)

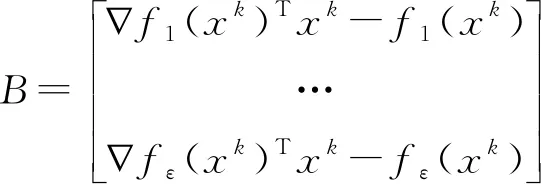
(11)

令：

?F(x)=?φ(x)=2ATAx-2ATB=0

(12)

求出φ(x)的平穩點，將A、B代入式(12)，得到ATAx=AT(Axk-f(k))，進而得：

ATA(x-xk)=-ATf(k)

(13)

式中：f(k)接式(14)計算。

(14)

ATA為對稱正定矩陣，即A為滿秩時，存在逆矩陣(ATA)-1，可通過式(8)得到φ(x)的穩定點：

xk+1=xk-(ATA)-1ATf(k)

(15)

3 實際工程應用

對玉林市某公路雙層軟土地基固結排水過程進行分析，利用基于工程現場實測沉降數據獲取的雙層軟土地基土工參數及模型對軟基沉降進行計算，為該公路軟基沉降量分析提供理論依據。

取玉林市某公路K28+280、K46+800斷面進行計算。兩斷面均為雙層地基，斷面K28+280的層高分別為5.4、8.4 m，斷面K46+800的層高分別為4.6、12.7 m。通過實際測量，得到各斷面的時間-沉降-固結度(見表1)，各斷面不同時間點各土層的固結度見圖1，各土層的相關土工參數ai、bi、cvi計算結果見圖2。

表1 兩斷面的時間-沉降-固結度

圖1 各斷面不同時間點各土層的固結度變化

圖2 兩斷面各土層土工參數計算結果

從表1可看出：K28+280、K46+800斷面的沉降量和固結度隨著時間的增加而增大。

從圖1可看出：2個斷面不同時間點各土層的固結度都逐漸增大，第一層地基的固結度大于第二層地基的固結度，但其固結度變化幅度逐漸變小，曲線逐漸平緩，并趨于某一范圍值。

從圖2可看出：2個斷面軟土地基的第一層土工參數逐漸增大，成層土層的豎向固結系數逐漸增大；第二層土工參數逐漸減小，土層的豎向固結系數逐漸減小；兩者的變化幅度都逐漸減小并趨于一個穩定范圍值。

基于軟土地基實測沉降數據計算地基土工參數，其精度較高，且收斂速度較快，可減少因誤差帶來的影響，將沉降量控制在工后沉降范圍內，能應用于公路建設項目中。

4 結語

將理論與玉林軟基公路相結合，建立基于現場實測沉降數據獲取軟土地基土工參數的優化模型，將工程現場實測數據與加載值輸入模型即可得到固結系數及土工參數。計算結果顯示，不同斷面各土層不同時間點的固結度逐漸增長，并慢慢趨近于某一范圍值。該方法可避免室內實驗的難點，且通過現場實測數據計算出的土工參數比實驗室內得到的土工參數更準確，避免了土樣在運輸、制作及實驗過程中發生變化造成結果不準確的困擾。