利用三維球性質直觀地推導麥克斯韋速度分布率

孫宇辰，張兆龍

（北京大學 物理學院，北京 100871）

現有大學熱學教材，都會涉及麥克斯韋速度分布律.然而現有教材與論文均未給出一個直觀同時嚴謹的證明方法.大部分教材或直接給出結果且僅證明結果符合要求［1］，或在列出方程 f（vx，vy，vz）＝ g（vx）g（vy）g（vz）后直接用“試探解”給出結果［2］.部分文獻通過解偏微分方程得到結果或給出解的唯一性證明，但這樣就會拘泥于數學公式而喪失了物理的直觀.筆者在課后思索并與同學討論后發現了一種較為幾何直觀且不用解偏微分方程的證明方法，這樣可以用大多數學生能理解的方法嚴謹直觀地證明麥克斯韋速度分布律，并使學生能更好地理解麥克斯韋速率分布與某方向上速度分布的關系并了解三維球的一個重要性質.

這篇文章的結構如下:在第二節引入了球坐標系及球臺側面積公式，在第三節用速率分布函數表示了速度分布函數，第四節通過常微分方程求解麥克斯韋速度分布函數，第五節為結束語.

1 關于三維球的性質

為了后文的證明，本節引入球臺側面積公式.如圖1所示，設三維球的半徑為 r，選定某一特定方向為x軸（圖中選取水平方向），球面上某一點與x軸夾角為 θ.下面求出單位 x軸上對應的球臺側面積:

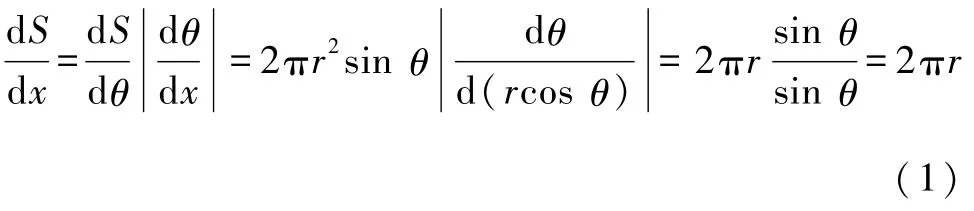
圖1 dS為球臺側面積，θ為球面上某一點與x軸的夾角

故三維球對應于單位坐標軸的面積與x選擇無關.

2 由速率分布函數推出某方向速度分布函數

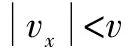
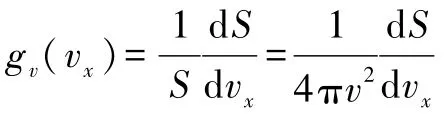
根據上文結論，容易得到

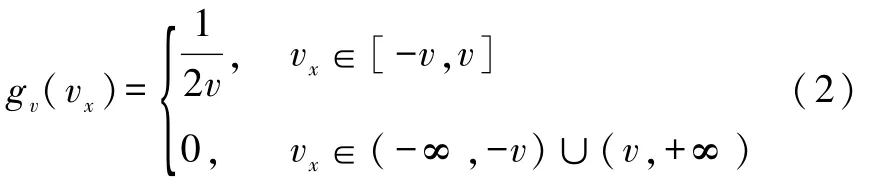
根據定義，有

該式得到了 g（vx）的用 f（v）表示的表達式.

3 求解

在大多數教科書中，均有［3］

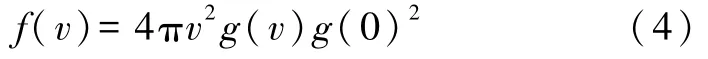
將式（4）代入式（3），有

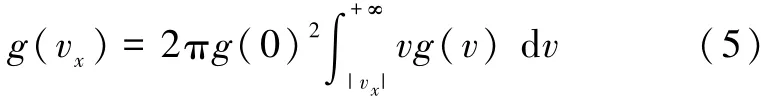
由于空間對稱性，g（vx）＝ g（-vx），vg（v）為奇函數，故有

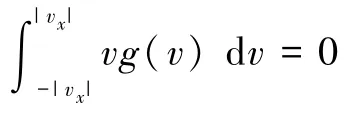
所以式（5）積分下界的絕對值可以去掉，即

左右對vx求導，移項，得

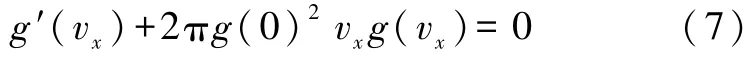
這是 g（vx）的一階線性齊次常微分方程，代入g（0），得

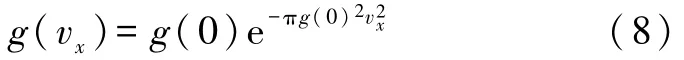
下面確定g（0）的值.由溫度定義可知

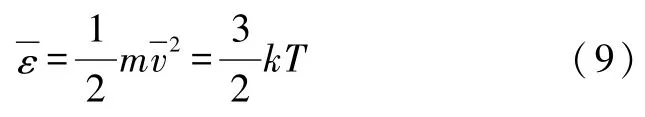
又

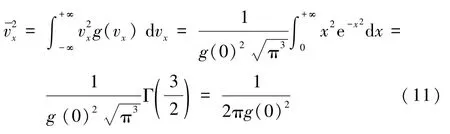
故有

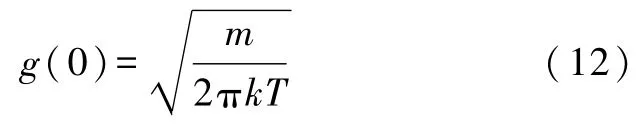
代入式（4）、（8），得

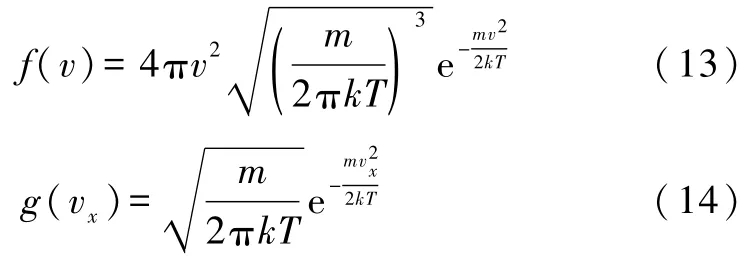
式（13）、（14）即麥克斯韋速率分布函數與某方向麥克斯韋速度分布函數.

4 結語

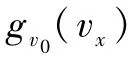
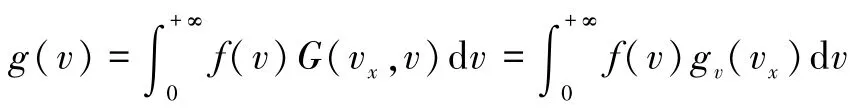
致謝:本文撰寫過程中得到了北京大學物理學院全海濤教授的指導，再次表示衷心感謝.