基于時空關聯分解重構的風速超短期預測

潘 超 李潤宇 蔡國偉 王 典 張永會

（1. 現代電力系統仿真控制與綠色電能新技術教育部重點實驗室（東北電力大學） 吉林 132012 2. 松花江水力發電有限公司吉林白山發電廠 吉林 132400）

0 引言

對風場進行風速預測有利于風場安全運行及含新能源并網的電網靈活調度[1-2]，但風速具有隨機性及低能量密度等特點，將導致電力系統運行的可靠性降低。因此，準確的風速預測對于風電并網及電力系統的運行變得越發重要[3]。

風速預測方法按照原理可分為物理方法[4]、統計學方法[5]及人工智能方法[6]。目前，大多數的國內外學者選擇BP 神經網絡[7]、支持向量機[8]、極限學習機[9]等人工智能方法對風速進行建模預測。雖然都取得了有效的預測結果，但這些淺層學習算法難以對輸入數據的深層特征進行挖掘，從而限制了模型的預測精度。因此，深度學習算法近年來備受關注[10]。文獻[11]運用灰色關聯決策分析了風速與功率的關系，并利用其灰色關聯關系和風速功率曲線建立了風功率預測模型，但未考慮空間相關性對預測模型精度的影響。已有研究表明[12]，卷積神經網絡（Convolutional Neural Network，CNN）可有效提取風速數據中隱藏的非線性特征。文獻[13]提出利用CNN 基于空間相關性提取多位置風機的空間特征，對風場多臺風機進行多位置多步預測，有效地提高了預測精度。對規模化風場進行風速預測時需要考慮時空相關特性。研究表明，為提高風速預測精度需對風速空間特征提取，該過程需要依靠高維數據信息，從而加重了模型計算的負擔，在效率方面存在一定弊端；現有優化算法僅適用于單次優化，不能執行多個優化控制，不能存儲和排序多個優化結果。

本文對多位置多步風速預測方法進行改進，在關聯分析環節提出一種風速矩陣時空關聯分解重構策略，運用改進灰色關聯分析風機的空間關聯度及單臺風機風速與功率的關聯度；提出時序控制的空間關聯優化算法，對風速矩陣關鍵信息進行優選重構。在多步預測環節改進卷積神經網絡，引入記憶單元構建卷積記憶網絡，進行空間特征提取及超短期預測。結合預測結果與實際數據，對所提方法的有效性進行驗證。

1 風速矩陣時空關聯分解重構策略

為了研究分析機群風速在時間和空間上的分布，從而提取關鍵特征信息，提出一種風速矩陣時空關聯分解重構方法。將風速時序波動按空間分解各時刻的風速信息，基于改進灰色關聯法分析（Improved Gray Relational Analysis，IGRA）風速矩陣的空間關聯性；通過時序控制的空間關聯優化算法對已分解的風速空間矩陣進行重構。

1.1 改進灰色關聯法

將機群的風速序列按空間分解為各時刻的風速子序列，通過確定參考數據列與對比數據列的幾何相似程度判斷其關聯性[14]。風速參考序列為

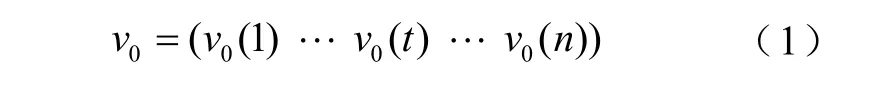
式中，v0為所選典型風機的風速序列；v0(t)為參考序列中第t時刻的實測風速值；n為時間點總數。

比較序列vij為

式中，vij為位于（i,j）位置風機的風速序列。

具體步驟如下：

1）對各序列進行初值化處理

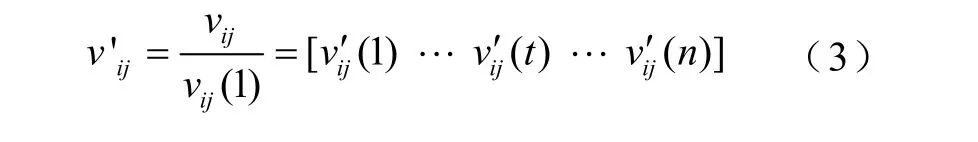
2）求參考序列與比較序列之差的絕對值序列為

式中，min minΔ(t)、max maxΔ(t)分別為不同時刻序列Δ(t)的最小值和最大值；κ為分辨系數，且κ∈(0，1)，κ越小表明分辨率越高。通過γ關聯度能夠計算各時刻不同風機的風速關聯性。

考慮不同時刻的風向差異，為了進一步分析風速序列的關聯性，改進灰色關聯方法，引入風向因子評價風向差，若風向差θ＞30°，則計算其風速序列關聯系數（m=1）；否則認為風向差較小，對風速波動相關性的影響可忽略（m=0）。定義風速序列關聯系數表征其關聯度為

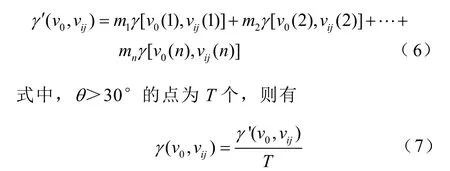
經由上述步驟，量化分析風速參考序列和比較序列數據，得到目標v0的特征系數。

1.2 風速空間關聯性分析

研究表明，風速預測精度受風速時間和空間兩方面限制[15-16]。本文將組合時間和空間因素構建三維風速時空序列，選取單時刻的空間風速信息定義為空間風速矩陣（Spatial Wind Speed Matrix, SWSM）St，如圖1 所示。其中，隨機選取圖1 中（i,j）位置風機為典型風機，定義其周圍8 臺風機為一階鄰域（鄰域-Ⅰ）；再外圍16 臺風機為二階鄰域（鄰域-Ⅱ），逐層類推，確定矩陣中各風機位置序列。

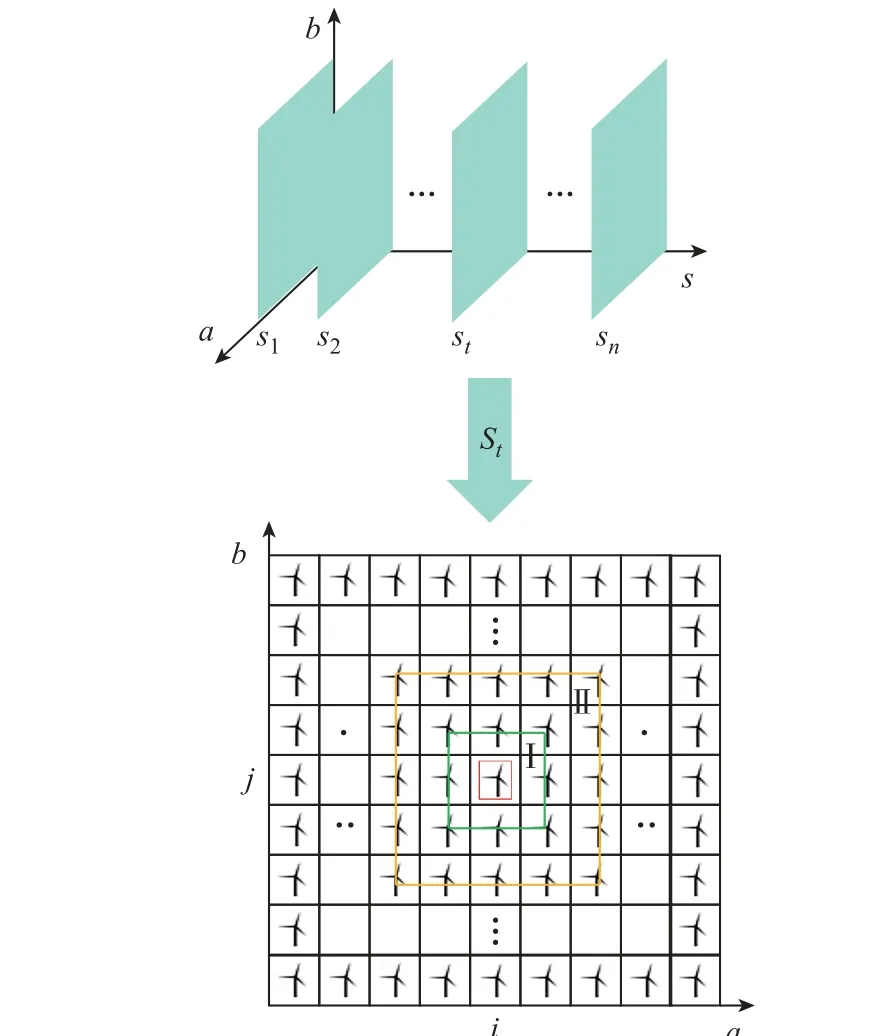
圖1 三維時空序列及SWSMFig.1 3-D spatiotemporal sequence and SWSM

東北地區某風場A 為研究對象（風場A 地形圖見附圖1），典型風機風速波動如圖2 所示。隨機選取A 中9×9 機群構建SWSM，利用2019 年8 月實測數據進行分析，計算典型風機與各鄰域的風速關聯度γ(v)，結果見表1。

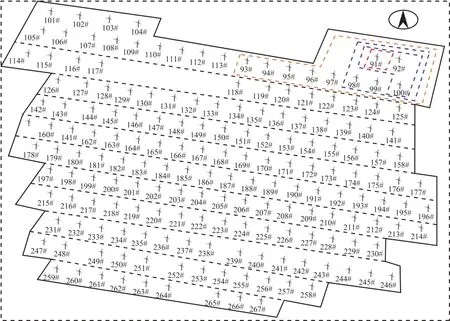
附圖1 風場A 地形圖App.Fig.1 Topographic map of wind field A

圖2 目標風機風速波動圖Fig.2 Target wind turbine wind speed fluctuation chart

表1 各鄰域風速關聯度γTab.1 Correlation coefficient γ for each neighborhood

表1 中鄰域-Ⅰ與典型風機的相關性最高，鄰域-Ⅱ次之，鄰域階數越高，關聯度越小。風速序列空間關聯的程度取決于典型風機與其鄰域的距離，距離典型風機位置越遠，空間關聯度越低。

由此，本文的風機矩陣重構規則為保留典型風機的鄰域-Ⅰ及其所在行列的風速信息，將其余位置信息歸零，便于對風機矩陣進行重構。

1.3 風速-功率關聯計算

對風電場進行風速預測的目的是為了預測風功率，進而提高新能源并網靈活性。因此，運用灰色關聯分析不同風機的風速與風功率之間的關聯度大小，從而選擇更具代表性的風機作為典型風機。計算風電場 A 中各臺風機風速-功率的關聯度γ(v-P)，將風速序列v作為參考序列，功率序列P為比較序列，結果如圖3 所示。

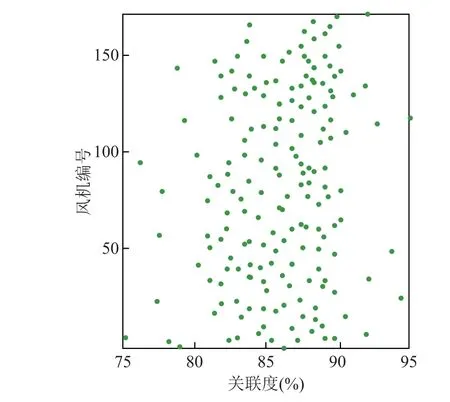
圖3 各風機風速-功率關聯度Fig.3 Correlation coefficient γ(v-P) of each wind turbine

圖3 中風機v-P關聯度主要集中于[80%, 90%]范圍內，對應風機均位于機群陣列中，表明這些風機受到尾流效應的影響較大導致關聯度較低；少數風機位于陣列邊緣，受來風向尾流的影響較小，關聯度較高。

1.4 時序控制的空間關聯優化算法

風機陣列中各風機具有不同的空間相關性，若考慮空間相關性進行風速預測需要通過局部特征擴展至全局，進而導致提取風場空間特征的復雜度增加。針對該問題，結合風速-功率關聯度和風機間的互關聯度，利用時序控制的空間關聯優化算法（Improved Spatial Association Algorithm, ISAA）優選出代表性風機，然后根據指定規則重構風機陣列，從而降低空間信息提取復雜度，提高風速的預測效率。

結合風場地理信息，將其視為動物種群生存森林，森林樹木表示各臺風機位置，各動物以綜合考慮風機互關聯度γ(v)和風速-功率關聯度γ(v-P)為原則對其進行搜索，數學模型可表示為

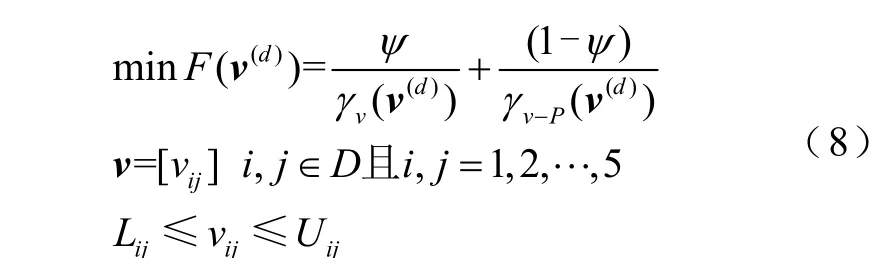
式中，v為二維空間變量矩陣；d為種群代數；ψ為權重系數；Lij、Uij分別為空間變量vij的上、下限。

ISAA 的主要步驟如圖4 所示。

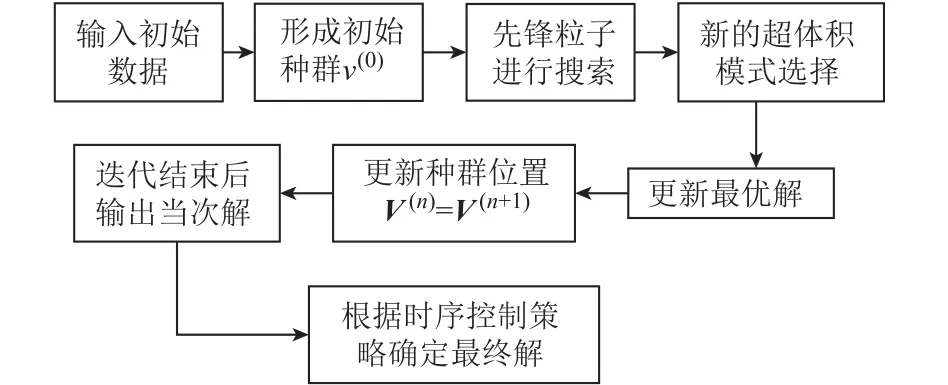
圖4 ISAA 主要步驟Fig.4 ISAA flow chart

為得到契合本文實際情況的最優目標選取，根據優選概率嵌入時序控制策略。當時序節點為?時，綜合排序每次優化得到的目標，得到概率最高的目標。

基于時序控制的空間關聯優化算法選取典型風機的思想是根據種群尋優算法改進的新型優化算法，具有較強的全局搜索能力，能夠不受區域規模限制搜索并找到克服局部最優的全局最優解。因此，ISAA 更適用于對風場中的風機序列進行優選。根據優化結果對SWSM 進行重構，生成SWSM*并輸入卷積記憶網絡，以提高空間特征提取效率及多步預測精度。

2 基于卷積記憶網絡的風速預測

當前多數風速預測方法由于忽略空間特征信息導致預測精度有限，且多數的淺層學習算法無法挖掘原始數據所隱含的深層特征。針對該問題，改進卷積神經網絡，引入記憶單元構建卷積記憶網絡（Convolutional Memory Network, CMN），模型對重構后的風速矩陣進行預測。可直接對CMN 輸入多個SWSM*，而無需將二維空間信息展開為一維序列，避免了空間信息丟失。其預測過程可分為兩部分，首先進行空間特征提取以實現維度壓縮及深層特征挖掘，進而利用記憶單元對風速進行多步預測，本文采用反向誤差傳播作為CMN 的訓練算法。具體結構如圖5 所示。

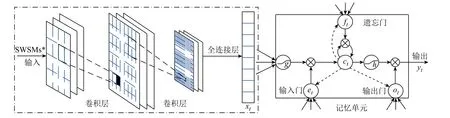
圖5 卷積記憶網絡結構Fig.5 CMN structure diagram

2.1 空間特征提取

CMN 的空間提取部分中，利用多個卷積核對輸入的風速矩陣逐一進行特征提取，得到長度較小的特征圖；然后在下一層中利用其他卷積核重復該步驟，直到生成的特征圖可通過全連接層展開成所需特征序列。

在CMN 架構中，同一層中的神經元之間不存在連接。此外，在不同網絡層中的神經元之間采用權重共享技術以簡化前饋和后向傳播過程。具體來說，前l-1 層中的特征映射與共享權重進行卷積，然后通過定義的激活函數來生成具有若干輸出特征映射的第l層，即

通過空間提取部分完成對 SWSM*中隱藏信息的挖掘和提取，以獲取空間特征中深層數據和關聯規則，提高風速預測精度。

2.2 風速多步預測

每個記憶預測單元擁有一個記憶細胞，其在時刻t的狀態記為ct。對ct的讀取和修改通過對輸入門et、遺忘門ft和輸出門ot的控制實現。ft在t時刻接收當前狀態xt與上一時刻隱藏層狀態yt-1，將所接收狀態經由σ激活使遺忘門的輸出值均在[0, 1]之間。當ft輸出為0 時，表示上一狀態的信息全部丟棄，當輸出為1 時，上一狀態信息全部保留。et的輸入經由非線性函數變換后，與ft的輸出疊加得到更新后的記憶單元狀態ct，最后輸出門根據非線性函數運算后的ct動態控制得到輸出yt。各變量具體計算公式為

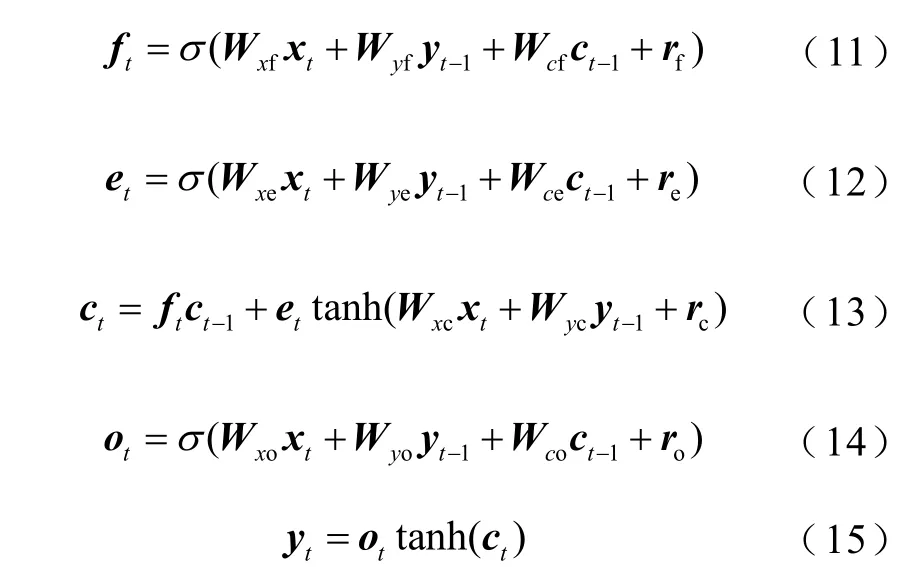
式中，Wxf、Wxc、Wxe、Wxo為連接輸入信號xt的權重矩陣；Wyf、Wyc、Wyo、Wye為連接隱含層輸出信號yt的權重矩陣；Wce、Wcf、Wco為連接神經元激活函數輸出矢量ct和門函數的對角矩陣；re、rc、rf、ro為偏置參數；σ為激活函數，通常為tanh 或sigmoid函數。

3 仿真分析

選取東北風電場 A 的風機布局信息，結合其2019 年8 月的實測數據進行預測。

設計用于風速多步預測的IGRA-ISAA-CMN 組合預測方法，設置ISAA 基本參數N=25，N′=5，g=50，?=9。CMN 的預測部分需確定輸入層時間步數，即考慮歷史序列長度，會影響模型計算復雜度及預測精度，若選用步數過大將降低模型預測性能，過小會引發預測誤差較大。文獻[13, 17]分別選用輸入步長為15 和20，本文通過試探在15～20 之間選擇步長18 為最佳，即輸入前18 時刻的歷史數據用于預測。特征提取部分選用三層結構，第一層設置為具有15 個3×3 卷積核的卷積層，第二層卷積層選用25 個3×3 的卷積核，第三層為全連接層，將卷積層輸出的二維特征展開成一維向量輸入預測部分。

評價預測結果時選取平均絕對百分比誤差ε1、方均根誤差ε2及日平均預測計劃曲線準確率ε3，構建適用于多位置、多步風速預測評價指標為

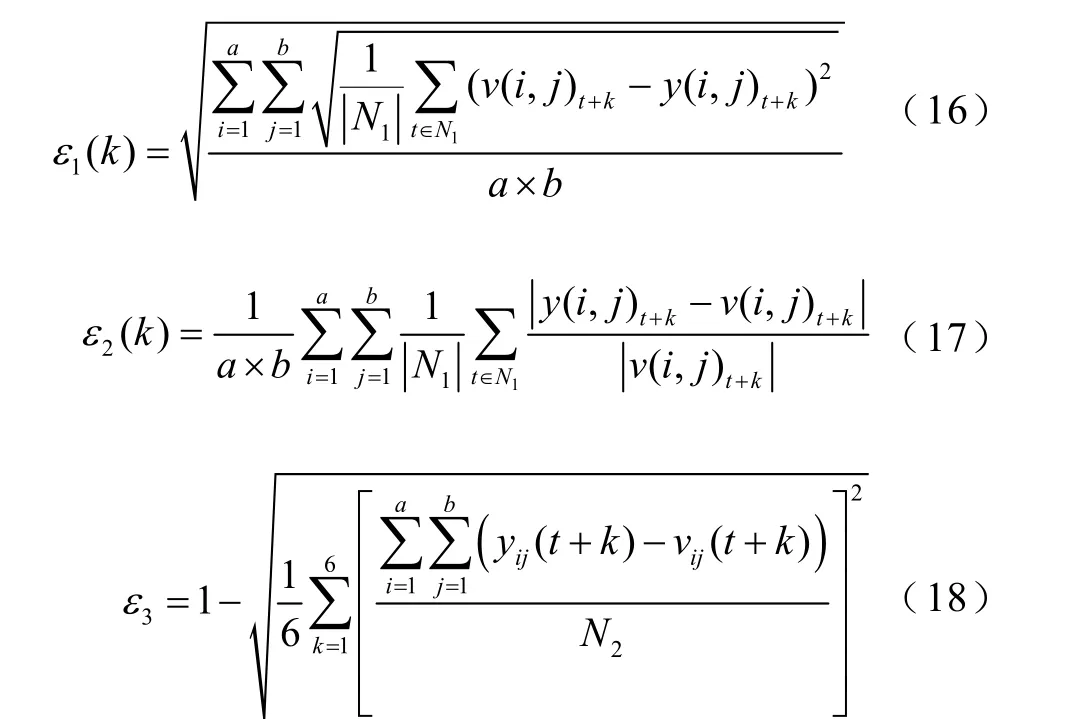
式中，k為預測步長；v為實測風速值；y為預測風速值；a、b分別為風電場陣列中的行數和列數；N1為測試樣本時間點總數；N2為總風機臺數。

3.1 基于IGRA-ISAA 的風機位置優選

為避免風機位置優選的特殊性，隨機選取1 個月內的9 個時刻利用ISAA 優選代表風機。定義搜索矩陣規模為5×5，對風場A 中風機陣列子區域命名區分，根據方向自北至南分為areaI～areaⅧ，從西到東分為area1～area18。初始化風機分布矩陣，矩陣元素為各風機編號，未安裝風機的位置為0。結果見附表1。

考慮到γ(v)受兩臺風機的風速差值影響，風速差越小，關聯度越大，故在選擇SWSM 時需優先規避補零風機；同時，未受尾流效應影響的風機γ(v-P)較高，故ISAA 默認優先選擇來風方向風場邊緣的風機。因此在進行優選時，引入加權綜合γ(v)和γ(v-P)的啟發規則，根據附表1 中ISAA 進行9次優選排序的結果顯示，矩陣area9Ⅴ為最后得到的風機矩陣。在此基礎上選取5 個先鋒動物(N′)在area9Ⅴ中對各臺風機再次進行優選排序，得到95 號風機為典型風機，如圖6 所示。將優選結果根據1.2 節中的風機矩陣重構規則進行重構，得到新的空間風速矩陣SWSM*。

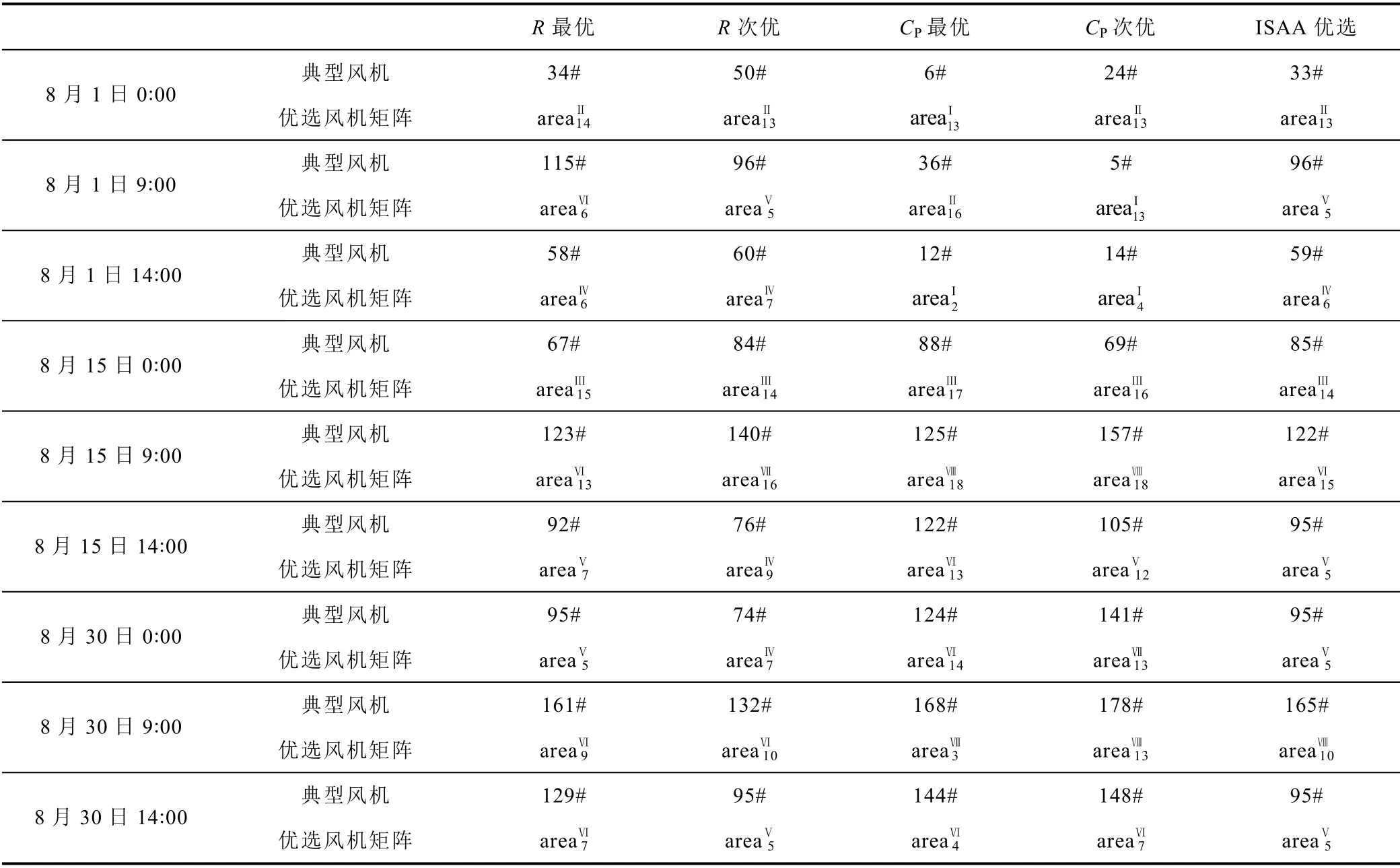
附表1 優選風機位置排序結果App.Tab.1 Preferred WT position ranking results

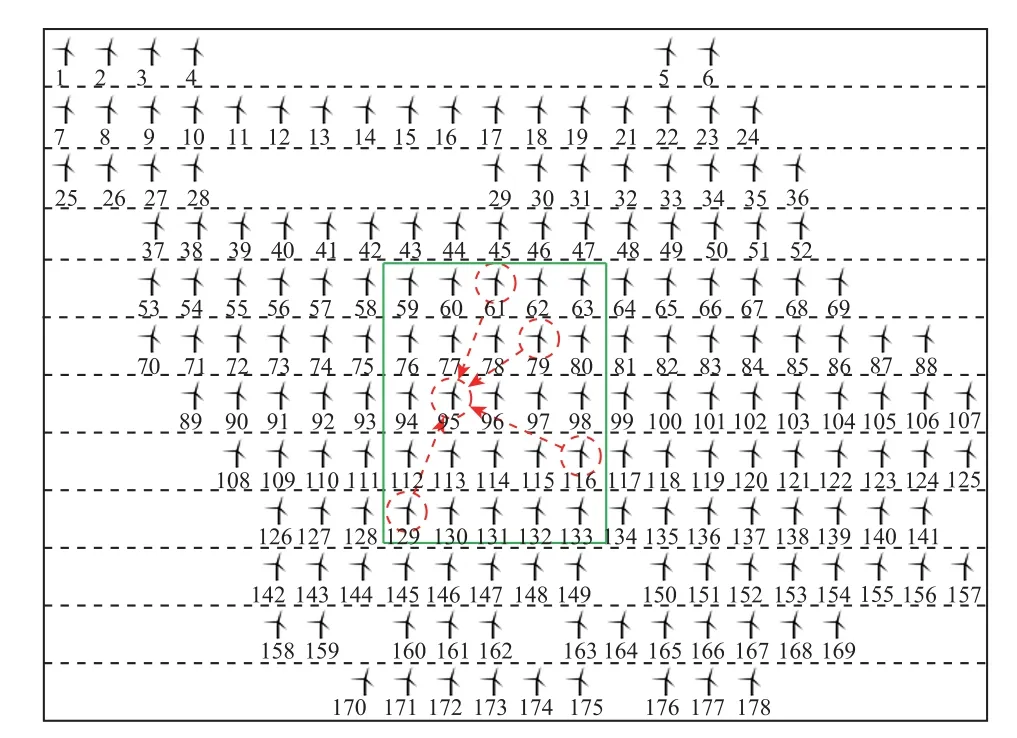
圖6 ISAA 優選結果Fig.6 The results of ISAA

選擇不同組合方法進行多步預測以驗證ISAA的有效性。其中，方法1 為ISAA-CMN，方法2 為CMN，預測結果見表2。

表2 中兩種方法均能有效預測風機陣列的多時刻風速，其中方法1 的訓練時長為309.87s，方法2的訓練時長為467.15s，預測效率提高了33.7%。證明ISAA 對SWSM*的優選重構，可顯著提高模型的預測效率。從預測精度來看，方法1 由于忽略了高階鄰域的風速信息，導致預測精度略微下降，其中ε1的下降幅度最高為0.07m/s，最低為0。由此可知，方法1 在提高預測效率的同時仍具有較高的預測精度。

3.2 風機預測精度分析

實測數據采樣間隔為10min，該月風速數據構成4 320 個SWSM，取前80%的風速樣本對風速組合模型進行訓練，對后20%風速進行預測。訓練集及測試集中的SWSM 經重構后輸入CMN 進行訓練及預測。為說明CMN 的有效性，隨機選取預測集中的連續時間點，對其進行0～1h、0～2h 和0～4h 的多尺度超短期風速預測，其中 0～4h 預測處理成15min 節點進行預測。將預測結果與持續法（ Persistence Method, PR）、 自回歸滑動模型（Autoregressive Integral Moving Average, ARIMA）及BP 神經網絡進行對比。PR 直接將當前時刻的實測值作為下一點的預測值；BP 使用單隱含層網絡結構，激活函數為 sigmoid 函數；ARIMA 采用ARIMA(1, 1, 1)模型進行訓練與預測。不同編號風機的不同尺度預測結果如圖7～圖9 所示。

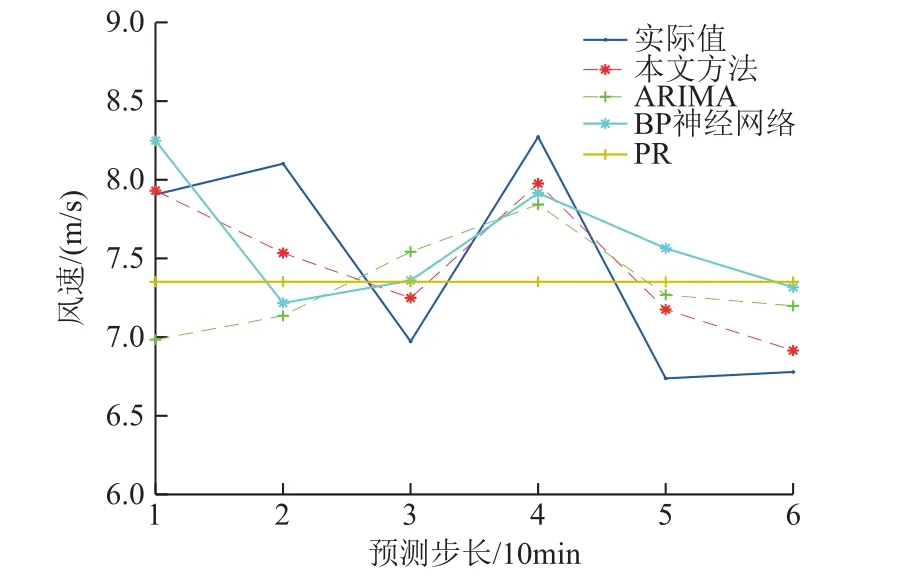
圖7 95 號風機預測結果對比Fig.7 Comparison of prediction results of 95# wind turbine

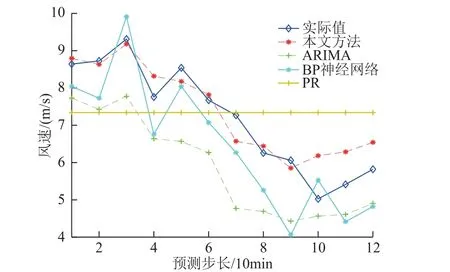
圖8 79 號風機預測結果對比Fig.8 Comparison of prediction results of 79#wind turbine

圖9 129 號風機預測結果對比Fig.9 Comparison of prediction results of 129#wind turbine

由不同時間尺度的預測結果可知，四種方法的預測結果均能在一定程度上符合實際風速波動情況。其中PR 由于其單一的預測結構導致隨著時間尺度的增加預測精度越來越低。ARIMA 和BP神經網絡無法直接對時空數據進行輸入，而需先將空間二維信息展開成一維，在此過程中將丟失大量空間相關信息，導致多數預測點與實際偏差較大。相對而言，本文所提方法不僅可直接輸入三維時空信息、挖掘空間數據中隱藏的深層特征及各空間位置關聯性，避免由于忽略空間信息導致預測精度下降，而且對風速的波動趨勢和細節變化均可較好擬合，使大部分節點都能得到較高的預測精度。同時，其誤差反向傳播的訓練算法也能有效減小預測誤差，因此CMN 模型能取得更為準確的預測效果。

在預測效率方面，BP 神經網絡的總訓練時長為513.12s，ARIMA 為 437.35s，本文所提出的ISAA-CMN 為309.87s。由于本文方法通過ISAA 優選重構空間風速矩陣，降低了輸入風速矩陣的空間復雜度，因此減小了CMN 的預測時長，提高了預測效率。為更好地驗證本文方法的預測準確性，對風機陣列0～1h 預測結果進行誤差計算，結果見表3。

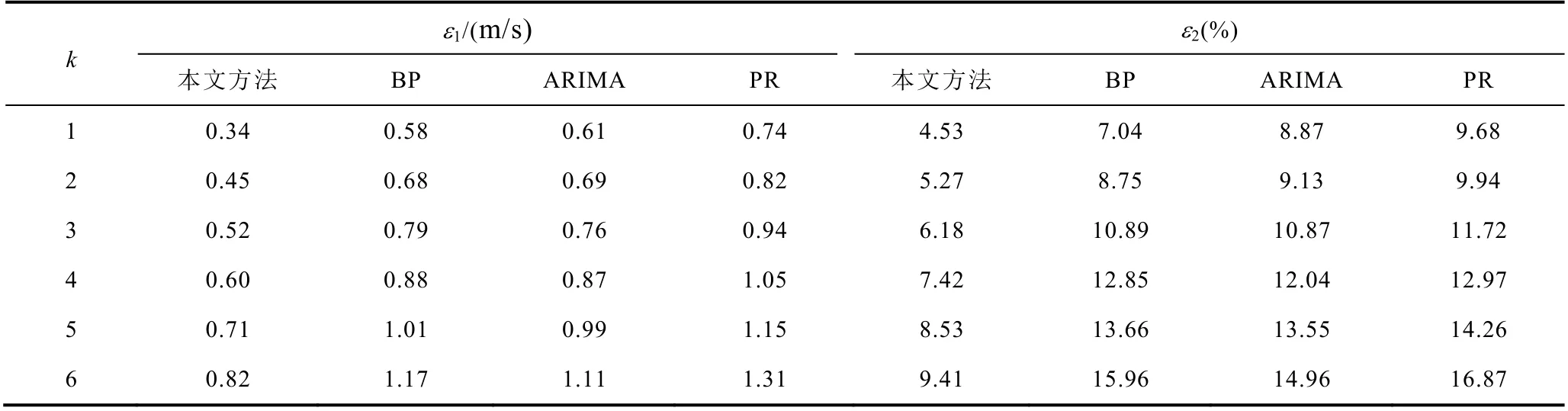
表3 不同算法預測誤差對比Tab.3 Contrast of prediction errors of different algorithms

結果表明，PR 的預測性能明顯弱于其他三種方法，且隨著預測步長的增加，其劣勢越發明顯。本文方法的6 步平均誤差為ε1為0.57m/s，ε2為6.89%，BP 神經網絡的平均誤差為ε1為 0.85m/s，ε2為11.53%，ARIMA 的平均誤差為ε1為0.84m/s，ε2為11.57%。因此，在總體平均性能及個體誤差的控制能力上，本文方法均有較好的表現，這得益于CMN在訓練過程中能夠對歷史風速信息選擇記憶或遺忘，其反饋神經網絡結構使其預測精度與其他算法相比有所提高。而BP 神經網絡的方均根誤差在1～2 步預測中誤差小于ARIMA，在3～6 步預測中誤差大于ARIMA，表明其更適用于較小步長的預測，如單步滾動預測。根據不同步長預測結果可知，隨著步長的增加，誤差存在一定累積，這主要是由于風速時間序列的混沌特性造成，該結論與文獻[18]一致。

3.3 泛化驗證

為避免所選地區經緯度及氣候特殊性的影響，故選取南方電網某風場B（地形圖見附圖2）驗證所提方法的泛化能力。由于所選地區為山區地形，與東北平原地區的集中式規模化風電場相差較大，該風場為依山脊走勢而建的小規模機群。

附圖2 風場B 地形圖App.Fig.2 Topographic map of wind farm

根據風場B 的地形及規模，設置ISAA 基本參數N=9，N′=3，g=30。基于風速空間關聯度γ(v)和風速-功率關聯度γ(v-P)優選結果如圖10 所示。對所選SWSM 進行重構、提取及預測，得到結果與不同方法對比分析，結果見表4 和表5。

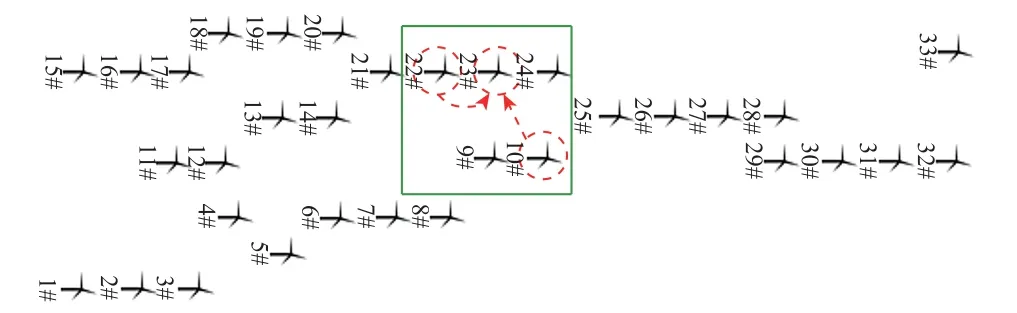
圖10 風電場B 優選結果Fig.10 Wind farm B optimization results

表4 風場B 兩種方法結果對比Tab.4 Comparison of results of two methods wind farm B

由于風電場B 中風機分布具有較大的分散性，從而降低了風速關聯度，導致在特征提取時涵蓋了大部分風機的空間特征信息。因此，表4 中兩種方法的誤差較為接近。由表5 可知，本文所提方法的預測結果相對于對比方法更能準確地反映風速變化趨勢。為證明所提方法的工程實用性，進一步對預測風速進行風功率轉換。選取基于最大風速出力模型[19]進行間接轉換（模型1），模型2 為直接利用本文模型預測風功率值，另外選取ARIMA 和PR 法進行對比分析，具體結果如圖11 所示。

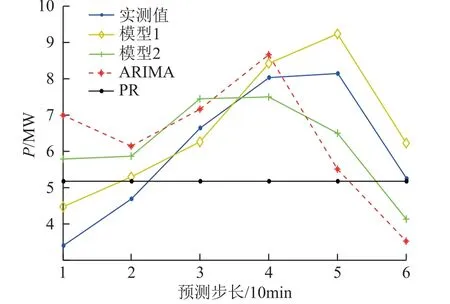
圖11 風場B 陣列風功率預測對比Fig.11 Wind farm B array wind power prediction comparison

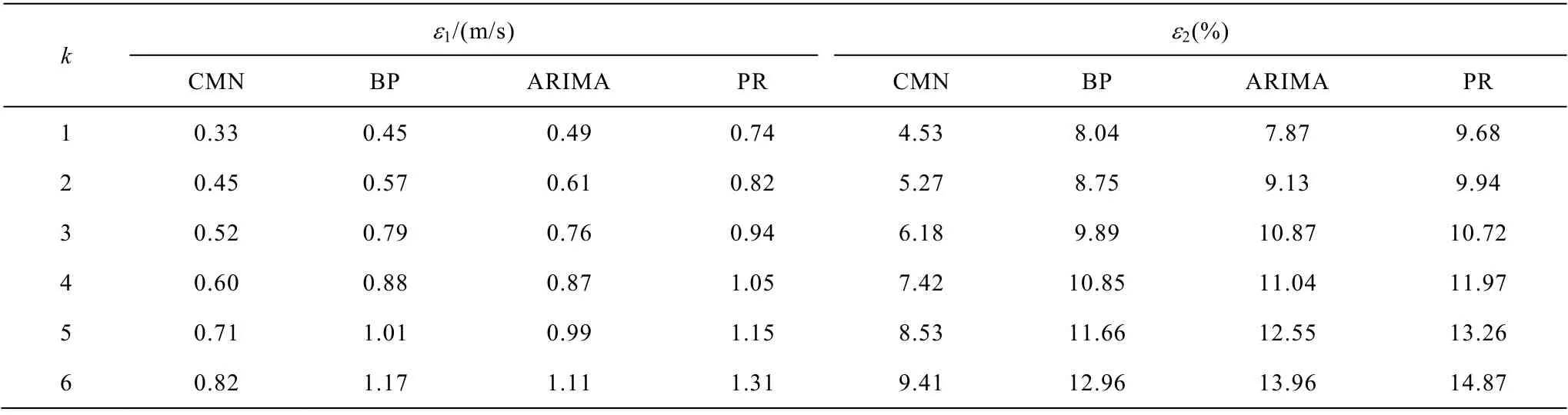
表5 風電場B 的不同算法風速預測誤差對比Tab.5 Contrast of wind speed prediction errors of different algorithms for wind farm B

圖11 中，模型1 的預測效果明顯優于模型2，其在各步預測中得到的預測結果均更貼近于實際值；ARIMA 能大致預測風功率變化趨勢；而 PR法僅在最后一個時刻值才與實際值較符合，說明該方法的預測原理并不適用于非線性序列預測。由于風功率數據中存在大量零點，從而導致直接預測模型對風速預測的準確性高于風功率預測。而通過間接法預測時可以將低于切入風速和高于切出風速的點剔除，將合格點進行風功率轉換，由此改善了預測效果。同時，間接法相對于直接預測在時間復雜度方面僅增加了5.36s，符合預測標準要求。模型 1 雖然在預測步驟上稍顯復雜但在精度上具有較大優勢，更具有實際意義。驗證了該方法不僅對平原規模化風場可達到較好的預測效果，也同樣適用于丘陵地區分散式風場，具有較強的適用性和泛化能力。

4 結論

基于風速關聯性研究多步風速及風功率預測方法，得出以下結論：

1）提出時空關聯分解策略，利用改進灰色關聯法能夠考慮風向因素分析風速序列在空間分布上的關聯特性。

2）通過時序控制的空間關聯優化算法可以對風速關聯矩陣進行排序優選，并按照指定規則重構空間風速矩陣，從而降低關鍵信息提取的復雜度，提高運算效率。

3）風速多步預測環節采用卷積記憶網絡能夠直接接收三維時空信息，深入挖掘風速數據中的隱含特征；基于時空關聯的卷積壓縮能夠避免由于忽略空間信息所導致的預測精度下降問題，對風速的隨機波動性具有較好的擬合效果。在此基礎上進一步預測風功率，并與實際數據對比，驗證了多步預測方法的準確性與適用性。

附 錄