不同流速下金屬網布篩管沖蝕壽命預測*

陳珊珊 時培忠 馮義 蓋靖安 樓一珊 翟曉鵬 史寶成

(1.長江大學石油工程學院 2.新疆油田分公司工程技術研究院3. 中石油吐哈油田分公司工程技術研究院 4. 中石油西部鉆探工程有限公司國際工程公司)

0 引 言

防砂失效會導致油井出砂、產液低，大幅降低油田的生產效益。篩網故障通常發生在完井與油井生產的過程中，但是故障原因卻難以準確確定，一般是堵塞與沖蝕共同作用下導致的失效[1]。因此，解決因沖蝕磨損引發的防砂失效，準確預測防砂壽命成為保證油田穩定生產的關鍵舉措。

當前對于防砂篩管的沖蝕研究多集中在篩管的性能評價上。S.MONDAL等[2-3]采用試驗研究與數值模擬相結合的方式來評估篩網性能，優選篩網。G.GILLESPIE等[4]以Troika油田為例，開發出防砂篩管沖蝕模型，用于驗證篩管的實際應用情況，但若要使用該模型預測篩管壽命，則仍需進行更多的測試評估。J.A.CAMERON等[5]以基本沖蝕理論為基礎，考慮砂粒大小和沖擊角度等因素，通過試驗結果獲得新的沖蝕數學模型，并以2%質量損失極限作為防砂失效標準，推導得到篩管壽命預測公式。但現有研究并沒有考慮井中使用的特定篩管系統，無法給出現有流動條件下預期油井壽命的定量指標，或者油井壽命會隨著流量的增加而縮短等問題。

針對防砂篩管沖蝕壽命難以預測的問題，本文以金屬網布復合篩管[6]為例，建立了全結構篩管模型，基于計算流體力學(CFD)進行數值模擬，根據沖蝕率的物理意義預測沖蝕壽命，以期為其現場應用提供理論指導。

1 仿真模擬計算模型

油井生產過程中夾帶的砂粒會對防砂篩管造成沖蝕磨損。防砂篩管沖蝕過程屬于固液兩相流作用下的沖蝕問題。由于涉及到的固體顆粒體積分數遠小于10%，計算區域為稀相空間，所以對固體顆粒采用離散相模型進行計算。相關計算模型如下。

1.1 流體控制方程

流體控制方程包括連續性方程和動量方程。連續性方程為：

(1)

動量方程為：

(2)

式中：ρ為流體密度,kg/m3；u為流體速度,m/s；x為坐標軸，i，j為空間方位；p為壓力,Pa；υ為連續相的運動黏度,m2/s；fi為質量力,N；f為流場中受到的其他力,N。

標準k-ε模型[7]是一種半經驗模型，基于湍動能k和耗散率ε二階相關量的輸送方程，具有精度高、適用范圍廣的優點，故采用標準k-ε模型。其控制方程為：

(3)

(4)

式中：k為湍流動能，J；μt為湍流黏度，Pa·s；σk、σε分別為k方程和ε方程的湍流Prandtl數，σk取1.0，σε取1.3；Gk為層流速度梯度產生的湍流動能，J；Gb為浮力產生的湍流能項，J；ε為湍流耗散率，W/m3；C1ε、C2ε、C3ε分別為經驗常數。

1.2 砂粒運動方程

砂粒在流體中主要受到流體作用力與顆粒碰撞作用力。顆粒碰撞作用力主要為顆粒間的碰撞作用力和顆粒與壁面的碰撞作用力。因為離散相體積分數遠小于10%，計算區域為稀相空間，所以可忽略顆粒間的相互作用。固體顆粒在兩相流中受到虛擬質量力、壓力梯度力、布朗力和重力等作用力，具體表達式如下[8]：

(5)

(6)

(7)

(8)

式中：up為砂粒速度，m/s；ρp為砂粒密度，kg/m3；d為砂粒直徑，m；Fy為y方向的其他作用力，包括虛擬質量力、壓力梯度力、布朗力和Saffman升力，N；CD為曳力系數；Rep為相對Reynolds數；α1、α2和α3為常數；FD為流體黏性阻力，N；gy為重力加速度，m/s2。

離散相模型可以忽略顆粒間的相互作用。顆粒與壁面材料發生碰撞時，將碰撞前、后速度分量的比值定義為恢復系數。采用G.GRANT和W.TABAKOFF提出的恢復系數[9]進行數值計算，其表達式為：

(9)

式中：εN為法相恢復系數；εT為切向恢復系數；α為顆粒軌跡與壁面的沖擊角度，(°)。

1.3 沖蝕模型

Fluent所使用的DPM沖蝕模型[10]為：

(10)

式中：Re為沖蝕率，kg/(m2·s)；C(dp)為顆粒直徑函數，C(dp)=1.8×10-9；f(α)為沖蝕角度函數，f=1；v為固體顆粒的相對速度；b(v)為顆粒相對速度函數；A為沖蝕面積，m2；mb為質量流率，kg/s。

2 篩管沖蝕模擬

2.1 篩管全結構建模

通過對實際篩管進行切片分析，研究金屬網布復合篩管的結構布局。金屬網布復合篩管由保護殼、多層篩網和基管組成。根據現場實際沖蝕破壞結果，主要沖蝕破壞位置為第一層篩網，考慮到模型計算工作量，建立了保護殼、雙層篩網和基管的三維模型。金屬網布的編織方法為麻花狀，通過測量計算，最終確定金屬網布的單元尺寸。

在建立金屬網布復合篩管三維模型的過程中，發現由于篩網的編織結構，使得Fluent進行布爾計算時多個界面線性相切，這對計算機性能提出了更高要求，無法開展后續數值模擬計算。因此，需要對金屬網布三維模型進行簡化并驗證其可行性。根據金屬網布的防砂機制，保留篩網的多孔流道結構，將其簡化為圓柱孔布置，并與相同尺寸的原始篩網建模，在附加保護殼建模的情況下進行數值模擬分析。經模擬結果驗證，簡化后模型與篩網編織模型的沖蝕區域位置吻合，故簡化后篩網可以應用于后續數值模擬。金屬篩網模型簡化前、后沖蝕云圖分布如圖1所示。

圖1 金屬篩網模型簡化前、后沖蝕云圖分布

確定金屬網布簡化模型后，建立復合篩管的全結構三維模型。其中保護殼流道采用錯位布置，金屬網布網孔直徑為120 μm。金屬網布復合篩管的三維模型如圖2所示。

圖2 金屬網布復合篩管三維模型

2.2 網格劃分及邊界條件

2.2.1 網格劃分

為保證計算結果精度，對主體計算區域這類復雜的工程結構采取非結構化的四面體網格，并進行加密，剩余流體域采用六面體網格劃分方法，并進行無關性驗證，最終確定當網格數為12 877 212個時，符合計算精度要求。最終網格劃分結果如圖3所示。

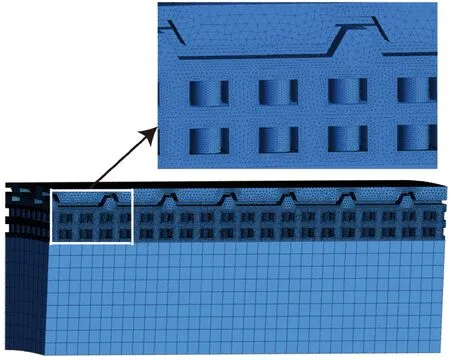
圖3 網格劃分結果

2.2.2 邊界條件

基于CFD模擬金屬網布復合篩管在固液兩相流作用下的沖蝕過程，仿真模擬計算主體區域是保護殼和兩層篩網。固液混合物以一定速度沖擊篩管，通過保護殼進入篩網，由于篩網的擋砂機制，大量砂粒與篩網的直接碰撞與觸底反彈碰撞使防砂篩網產生塑性變形；部分砂粒進入篩網，對篩網造成切削磨損。固液混合物沖蝕入口為保護殼外界面，出口為壓力outflow，離散相與沖蝕壁面為彈性反彈。

2.3 壽命預測

G.GILLESPIE等[11]通過對不同篩管類型進行完井模擬，提出了基于質量損失的篩管防砂失效判斷依據，認為繞絲篩管質量損失2%，縫寬變大0.05 mm；金屬絲篩管質量損失8%，出砂量會嚴重增多，篩管防砂失效。其中8%的質量損失極限為保守值，本研究通過大量模擬與試驗對比，最終取5%為質量損失極限。

CFD獲得的沖蝕率定義為單位時間和單位面積下金屬材料損失的質量，故以5%作為質量損失極限，以第一層金屬網布的平均沖蝕率為計算依據，推算出金屬網布復合篩管的沖蝕壽命[12]。沖蝕壽命預測公式為：

(11)

式中：t為沖蝕破壞時間，s；Re′為第一層篩網的平均沖蝕率，kg/(m2·s)；ΔGmax為第一層篩網的5%質量損失量，kg。

2.4 模擬可行性驗證

對金屬網布篩管試件進行不同速度的沖蝕試驗，得到不同速度下防砂篩管的沖蝕壽命，進而驗證全結構金屬網布復合篩管仿真模擬結果的可行性。

2.4.1 試驗裝置

采用水射流噴射含砂液體沖擊試件表面的方法進行沖蝕試驗，測試篩管試件的沖蝕破壞時間及形貌，分析不同流速、不同篩管結構對篩管沖蝕壽命的影響規律。篩管試件沖蝕試驗裝置流程如圖4所示。

圖4 沖蝕試驗裝置流程圖

2.4.2 試驗方法

試驗試件采用金屬網布復合篩管切片，試件尺寸為200 mm×115 mm，擋砂精度為120 μm。砂粒質量分數為40%～60%，砂子粒徑為100～120 μm，噴嘴距離為40 mm，沖擊角度為90°，設定沖擊速度v分別為20、30、40和50 m/s。

試驗過程中，根據沖擊速度不同，分為多個輪次，每個輪次加砂約75 kg，每輪次加砂沖蝕持續破壞時長約35 min。當試件過濾層完全破壞、底部出現明顯漏砂時，沖蝕破壞試驗結束。累計篩管的有效沖蝕時長，即為該速度下的金屬網布復合篩管沖蝕壽命。

2.4.3 試驗結果與模擬結果

沖蝕試驗結束后，拆解并觀察試件的破壞形態。試件由保護殼、多層金屬網布和基管3部分組成。通過觀察發現，保護殼出現明顯沖蝕孔，第一層金屬網布出現圓形沖蝕孔，且破壞面積普遍遠大于外保護罩的破壞面積。第二層金屬網布破壞形態與第一層類似，但沖蝕的面積減小，內部導流層出現一定程度的沖蝕破壞。這是由于試驗采取的沖蝕角度為90°，砂礫撞擊試件表面幾乎完全是垂直的應力，造成嚴重的塑形變形[13]。

統計不同流速下的金屬網布復合篩管沖蝕壽命，與仿真模擬壽命預測結果相差不大，誤差在10%以內，說明仿真模擬預測金屬網布復合篩管沖蝕壽命具有可行性。隨著流速增加，沖蝕壽命也在不斷縮短。仿真模擬與物理試驗壽命預測對比如圖5所示。

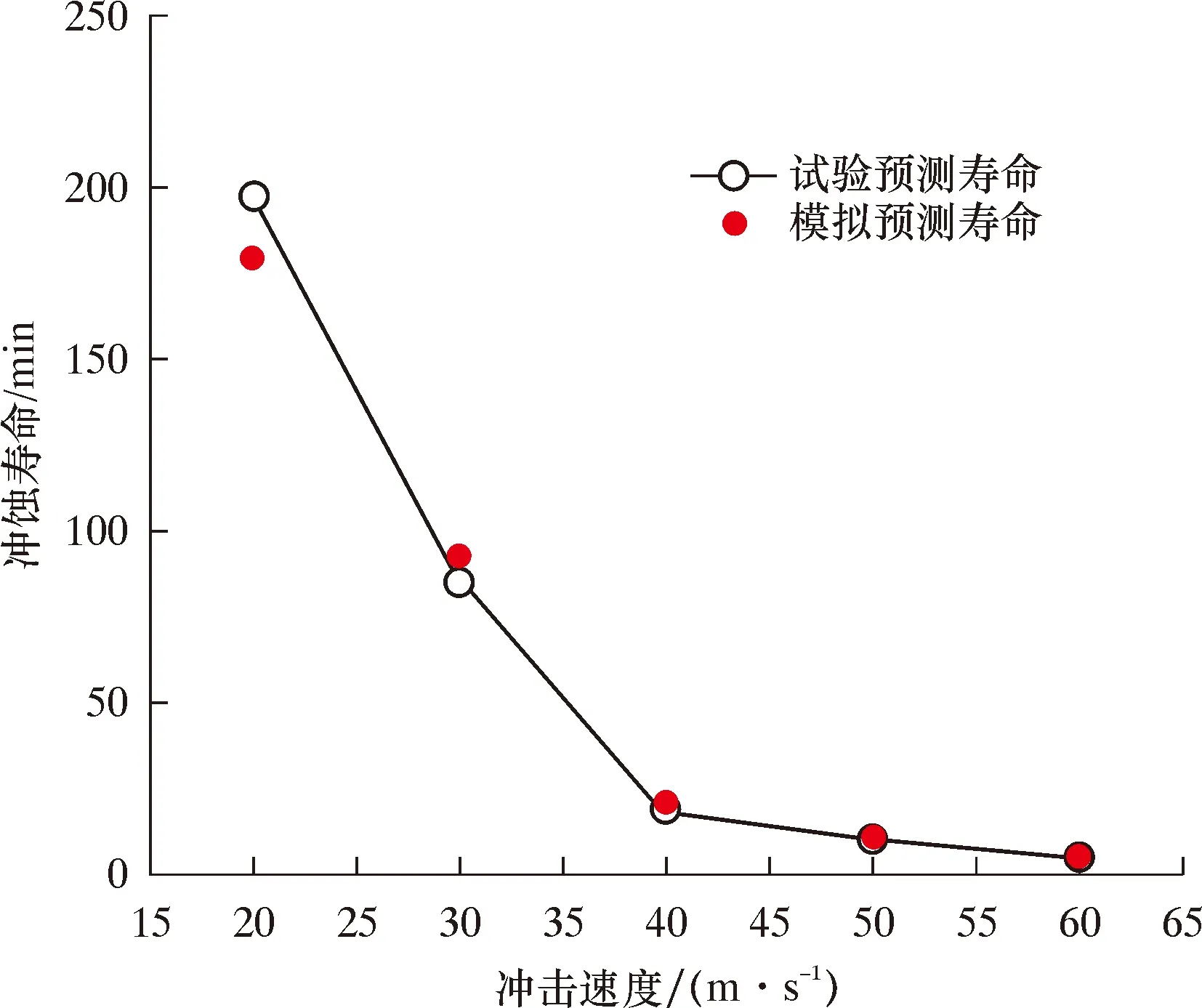
圖5 不同沖擊速度下模擬與試驗預測壽命對比

2.5 模擬結果分析

設置入口速度為40 m/s、含砂質量分數為50%進行數值模擬，得到金屬網布復合篩管的沖蝕速率分布，如圖6所示。從圖6可以看出，沖蝕速率最大值分布在第一層篩網，且集中在與保護殼流入通道下的交錯區域。這是由于保護殼的特殊結構，使得流體流經保護殼進入金屬網布的過程中，流體方向發生轉變，固體顆粒在交錯處形成局部熱點，造成該區域更加容易受到沖蝕破壞。第一、二層篩網的沖蝕率分布相同，第二層的沖蝕率小于第一層，這說明流體從第一層篩網流經第二層篩網的過程中，運動方向沒有發生太多改變，但由于第一層篩網阻隔了大量砂粒，使得第二層篩網的沖蝕程度遠小于第一層。隨即分別統計了20～60 m/s沖擊速度下的平均沖蝕率，并分析各個元件之間的沖蝕規律，結果如表1和表2所示。

圖6 沖蝕速率分布云圖

表1 不同沖擊速度下篩管各元件的平均沖蝕速率

表2 不同沖擊速度下篩管各元件之間平均沖蝕速率比值

由表1和表2可以看出：第一、二層篩網與保護殼的平均沖蝕速率比值分別為2.476和1.053；第一層與第二層篩網的平均沖蝕率比值為2.351，即第一層篩網在沖蝕過程中最先發生沖蝕破壞。

3 實例應用

A區塊油井井深在1 400～2 800 m之間，完井方式為裸眼完井，采用優質金屬網布防砂篩管，內置金屬網布的擋砂精度均為120 μm，井身結構為水平井。根據各井的產油和產液情況，結合含水體積分數，對各井口的產出液密度進行計算，進而計算各井口的質量流量、體積流量以及流速。根據已有的出砂井現場數據，使用Rosin-Rammler模型[15]對現場出砂井砂粒的粒徑分布進行分析，并提取出砂井現場油水混合物密度和黏度等信息，綜合分析模擬參數的設定方式，得出粒徑中值和最頻粒徑為240 μm左右。含砂體積分數設定為0.5%。仿真模擬與現場監測壽命對比見表3。

由表3可以看出，本文建立的沖蝕壽命預測模型在實際應用中誤差小于10%，符合工程壽命預測要求。

表3 仿真模擬與現場監測壽命對比

4 結論及認識

(1)通過金屬網布復合篩管仿真模擬獲得篩管沖蝕率，以5%質量損失極限作為防砂失效標準，推算出篩管防砂壽命，與試驗結果符合率達到90%。這為篩管沖蝕壽命預測提供了一種新的思路和方法。

(2)不考慮砂粒堵塞，流速與沖蝕壽命呈現負相關；第一層篩網為最先被沖蝕破壞的部件。

(3)本次防砂篩管模擬是不考慮砂粒堵塞工況的沖蝕預測模型，考慮砂粒堵塞工況的沖蝕模擬仍需進一步研究。