基于響應面法的旋流器直徑與處理量關系研究*

劉志濤 田洋陽 宋偉 趙季初 白通 崔之健

(1. 山東省地勘局第二水文地質工程地質大隊 2. 山東省地熱清潔能源探測開發與回灌工程技術研究中心3. 西安石油大學石油工程學院 4.陜西省油氣田特種增產技術重點實驗室 5. 中國石油青海油田采油一廠)

0 引 言

地熱是一種可持續利用的環保型清潔能源，很多國家對地熱資源的開發利用都在逐年加大力度與投資[1]。地熱回灌式開采能夠維持區域儲層壓力，并且采出水經處理后回灌可以有效減輕地熱流體排放對土壤、地表水體和淺層地下水體的熱污染和化學污染。但地熱回灌尾水中攜帶的懸浮物、泥砂、氣體和微生物會導致熱儲層堵塞，地熱回灌堵塞一直是制約地熱開發利用的難題[2]。因此，需要設計完備的地上尾水過濾系統對回灌流體進行處理，其中去除尾水中的泥砂是必不可少的工藝過程。旋流除砂裝置具有以下優點[3]：①除砂處理時間短，分離效果好；②結構緊湊，占地面積小；③內部無轉動部件且不需要外部能量帶動，操作簡單安全，易于維護，勞動強度低；④可通過串聯或并聯連接滿足不同除砂效果和處理量要求，適應性廣。故本文采用旋流分離技術對尾水中砂粒進行粗分離。

液固旋流器的尺寸對分離效果起決定性作用。但目前液固旋流器最主要的設計參數是筒體直徑，仍按經驗方法取值，具有較強的主觀性和隨機性。處理量直接影響旋流分離中液相入口流速，也是旋流器結構設計的考慮因素之一，通常作為操作參數研究其對分離效率和壓降的影響。處理量和筒體直徑一直是研究的重點，相關研究成果較多。ZHAO B.T.等[4]將旋風分離器尺寸、操作條件和多相特性等聯系起來，定量研究了旋風分離器尺寸和操作參數對顆粒切割粒徑的影響。M.AZADI等[5]先利用解析方法，研究了入口速度對不同旋風分離器幾何形狀和壁面粗糙度的影響，發現過大的增加進口速度不一定會提高更細顆粒的分離效率，反而會導致旋流器的壓降更高。隨后M.AZADI等[6]又針對3種不同尺寸的旋流器，利用數值模擬方法研究了入口速度和旋流器尺寸對旋流器水力分離過程和效果的影響，發現隨著旋流器尺寸增加，切割直徑和壓降也隨之增加。S.M.MOUSAVIAN等[7]通過數值模擬，研究了入口流量和旋流器筒體尺寸等結構參數對分離效率和壓降的影響，但未考慮入口流量與筒體尺寸之間的關系。W.P.MARTIGNONI等[8]采用RSM和LES研究了旋風分離器幾何形狀的影響，以改進旋流器性能，分析了幾何效應對工程的影響。

除了傳統的單一變量優化方法，響應面優化、神經網絡和多目標優化等方法也應用于旋流器結構設計中，對于不同幾何參數或性能標準之間的內在關系有了更深入的理解。K.ELSAYED等[9]利用神經網絡和響應面優化法研究幾何參數對性能的影響，優化了Stairmand標準旋流器的結構。L.M.ROSA等[10]針對FCC催化劑進行試驗研究，分析不同入口速度和負載比下旋流器中顆粒的運動，研究表明入口速度和固體載荷比對旋流器切割粒徑有顯著影響。P.SING等[11]采用Co-Kriging Surrogate模型多目標優化旋風分離器的幾何形狀，該模型可作為多目標優化算法的替代，用于識別有限解的Pareto解集。R.D.LUCIANO[12]基于多目標優化，研究不同幾何形狀旋流器對壓降和分離效率的影響及壓降和分離效率之間的內在關系，建立了可靠的多目標優化模型。

由此可見，關于不同幾何參數和操作參數的研究較多，并獲得了不同條件下幾何參數或操作參數最優范圍，工程上難以直接應用。但處理量等操作參數和筒體直徑等幾何參數之間緊密相關，而關于二者關系的研究較少。劉正權[13]通過線性回歸方程對常見煤泥重介質旋流器直徑與處理量的關系式進行驗證，研究了入口壓力與處理量和直徑的關系，建立了新的旋流器直徑與處理量關系式，可作為煤泥重介質旋流器設計計算和選型的依據。張澤幫等[14]通過對結構參數、操作參數和物性參數的對比分析，得出兩種臨界顆粒直徑及處理量的變化曲線和主要影響因素，并通過參數對比得到參數合理選擇區，可以用于指導碟式離心機結構設計。綜上，處理量與筒體直徑之間的關系研究仍不充分，缺乏可供工程設計直接應用的筒體直徑。

本文采用數值模擬和響應面分析方法，在筒體直徑和處理量之間定性分析的基礎上，建立筒體直徑與處理量的定量關系，并通過室內試驗驗證模型的準確性。本文獲得的經驗關系式可為回灌流體除砂處理提供參考。

1 響應面分析法

響應面分析方法(Response Surface Methodology，RSM)：設計一套試驗方案，將獲得的試驗數據通過多元二次回歸方程來建立影響因素與響應值間的數學模型，并以此數學模型來確定最優解，最終完成多變量求解。該方法將復雜的多變量未知數學關系在一定區間內轉換為簡易的低階多項式數學關系，可大幅降低運算難度，是解決實際問題行之有效的數學方法，目前得到了廣泛應用。

1.1 響應面概念與模型

設變量y與x1,……,xp有關系，設為Ey=f(x1,……,xp)。例如，變量y與因素x1、x2有關系，設為Ey=f(x1,x2)。如果已知Ey=f(x1,……,xp)的關系，則y與x1,……,xp的關系可全面掌握。

若Ey=f(x1,……,xp)的關系未知，則需要進行試驗或抽樣，由有限次試驗所得數據來估計Ey=f(x1,……,xp)(由部分來說明全體)。可采用麥克勞林或泰勒展開式來估計Ey=f(x1,……,xp)，即：

(1)

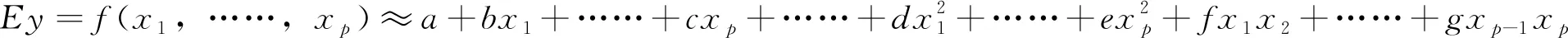
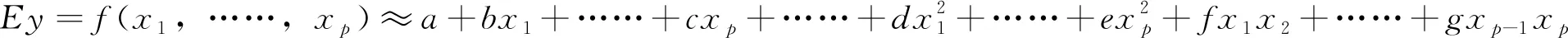
1.2 響應面分析試驗設計

中心組合設計(Central Composite Design，CCD)和Box-Behnken設計(BBD)是常用的兩種響應面分析試驗設計方法。中心組合設計也稱星點設計，設計表在兩水平設計的基礎上加上極值點和中心點構成。Box-Behnken設計同樣是一種常用的響應面優化試驗設計方法，三因素BBD試驗設計試驗點分布情況如圖1所示，立方體中邊線的中點為試驗點。

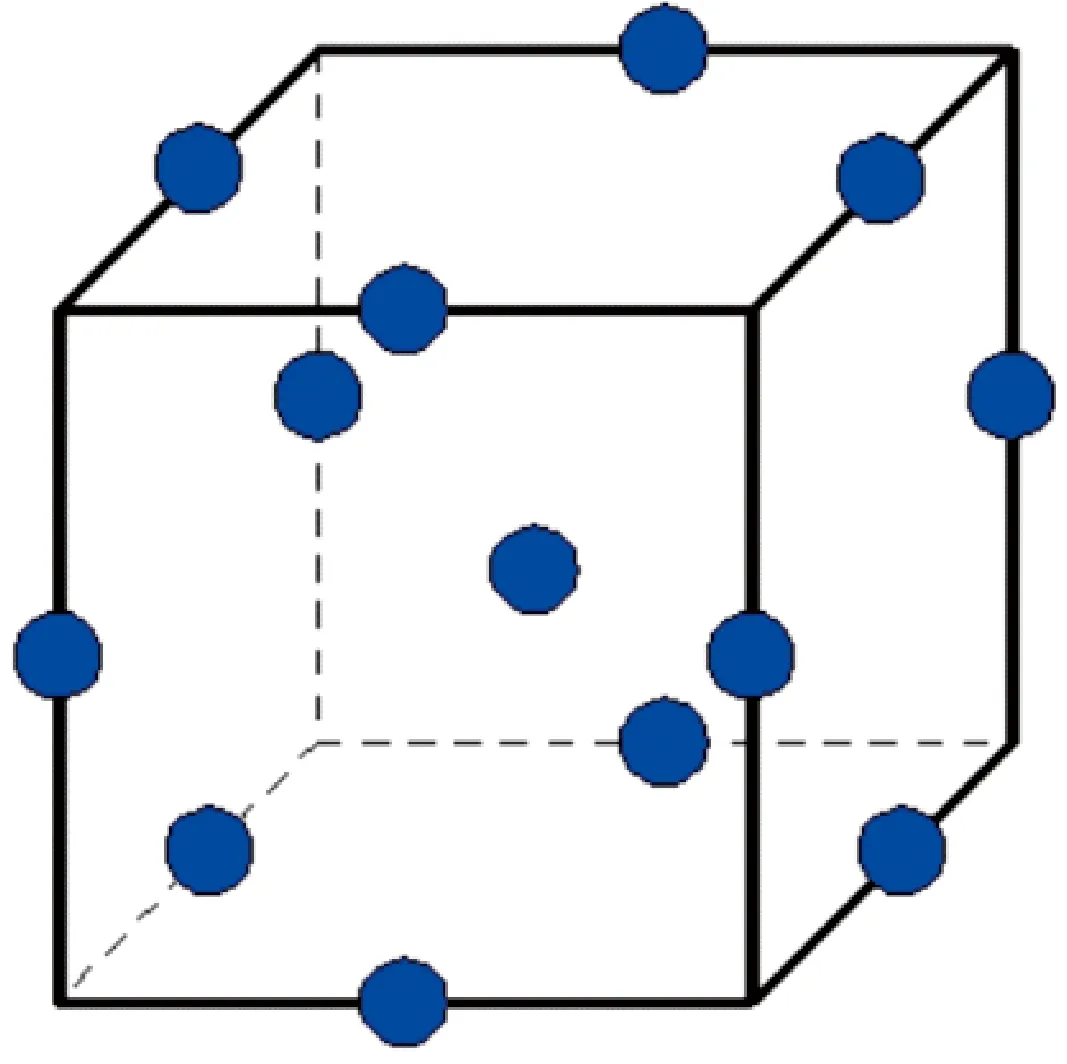
圖1 三因素BBD試驗設計試驗點分布情況

最為常用的響應面分析擬合方法是多項式法，若因素關系較簡單則可選擇一次多項式，若因素間存在相互作用則可選擇二次多項式，若因素間相互作用更加復雜，則可選擇三次甚至更高次數的多項式。一般應用時大多選擇二次多項式。

2 旋流分離器數值模型

2.1 幾何模型及網格劃分

本文采用的旋流分離器結構如圖2a所示。利用SolidWorks繪制旋流器流體域的三維幾何模型，不同直徑筒體幾何尺寸如表1所示。以旋流器筒體直徑250 mm為例，將建立的旋流分離器流體域三維模型導入ICEM中進行網格劃分，利用Robust(Octree)方法劃分非結構化網格，確保網格質量在0.34以上。網格劃分如圖2b所示。

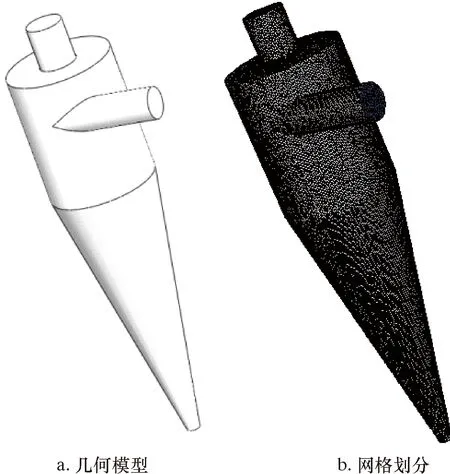
圖2 旋流分離器模型及網格示意圖

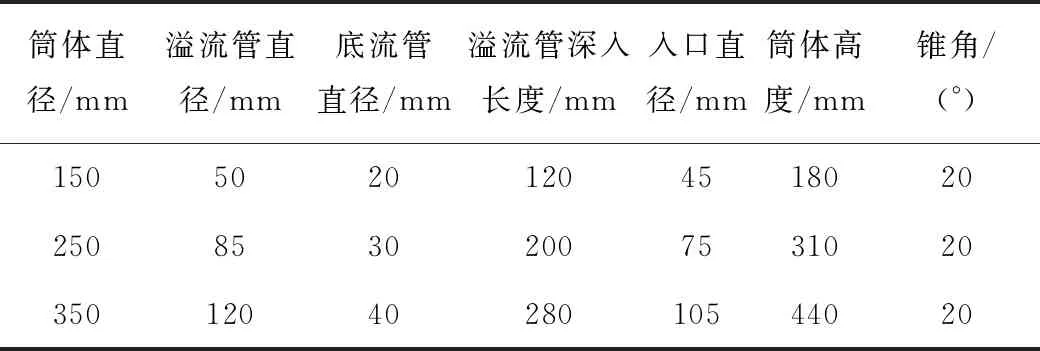
表1 不同筒體直徑的幾何尺寸

為了保證數值結果與網格數量無關，針對直徑250 mm的旋流器劃分了5種不同數量的網格，分別為80萬、98萬、136萬、188萬和277萬個，并將z=-0.20 m處的速度做對比，結果如圖3所示。

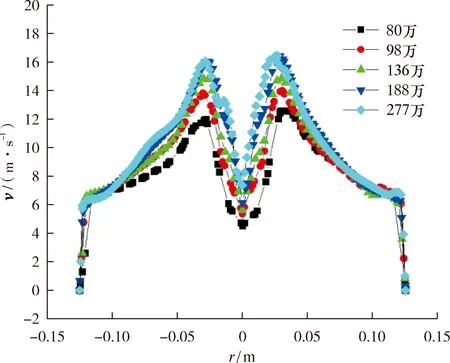
圖3 不同網格數量下z=-0.20 m處的速度對比

由圖3可知，隨著網格數量不斷增多，z=-0.20 m處的速度峰值不斷增大，從12 m/s逐漸增大到16 m/s。但是網格達到了188萬后繼續增加網格數量，速度分布基本不變。綜上，當網格數量達到188萬后，繼續增加網格數量對計算結果影響較小，故網格數量采用188萬。

2.2 數學模型

湍流模型采用雷諾應力湍流模型，多相流模型采用離散相模型。在實際數值模擬中，為了加速收斂，減少數值計算量，相間作用力只考慮阻力。入射砂粒密度為2 600 kg/m3，體積分數為1%，粒徑為1×10-4m。

壓力-速度耦合采用SIMPLE格式，壓力的離散具有二階精度，湍動能和湍動能耗散率采用一節迎風格式，雷諾應力采用一階迎風格式。入口速度類型為速度入口，方向垂直于入口面，大小根據處理量和入口面積計算。以處理量30 m3/h、直徑250 mm的旋流器為例，計算入口邊界參數，見表2。溢流出口和底流出口邊界設置為自由出口。在進行DPM模型計算時，溢流邊界屬性設置為Escape，底流邊界屬性設置為Trap。壁面采用無滑移邊界，采用標準壁面函數來計算。

表2 ?250 mm旋流器入口邊界參數

3 筒體直徑與處理量關系

3.1 筒體直徑與處理量的定性關系理論分析

旋流器的處理量通常用單位時間內通過入口管的液固體積流量表示，可由入口面積與入口流速乘積計算得到，其中入口管中平均流速與旋流器內壓力降有關。國內外學者提出的計算壓力降基準面的位置與形狀的觀點較多，主要包括最大切向速度軌跡法、等壓面法和空氣柱界面法[15]，其中最大切向速度軌跡法應用最為廣泛。本節基于最大切向速度軌跡法，利用數值模擬所獲流場特性，分析筒體直徑與處理量的定性關系。

針對?250 mm旋流除砂器，從不同z軸高度處的切向速度vt分布圖(見圖4)可以看出，在漩渦溢流管外圍的環形空間，切向速度沿徑向變化不大。在錐體部分，切向速度沿徑向有明顯的變化，各相應斷面的器壁切向速度最小，由器壁沿徑向往軸心其速度逐漸增大，當達到漩渦溢流管入口內壁附近的相應位置時出現最大值，隨后又減小。最大切向速度所在位置rm大約為0.25倍的旋流器半徑(rm=0.25R)，換算為溢流管半徑ro，則有rm=0.7ro。z=-0.10 m為溢流管下端截面，故在溢流管處速度為0。

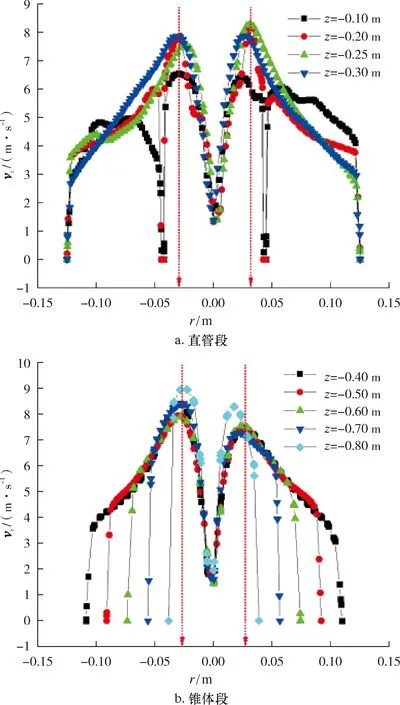
圖4 直管段不同z軸高度處切向速度vt分布

旋流器分離過程中流體運動的切向速度分布遵從組合渦運動規律，切向速度與流體旋轉半徑的n次方成正比。將切向速度和旋流器半徑做圖，可獲得準自由渦運動的速度分布特征，如圖5所示。擬合后切向速度指數n=0.557，具體切向速度分布函數如下：

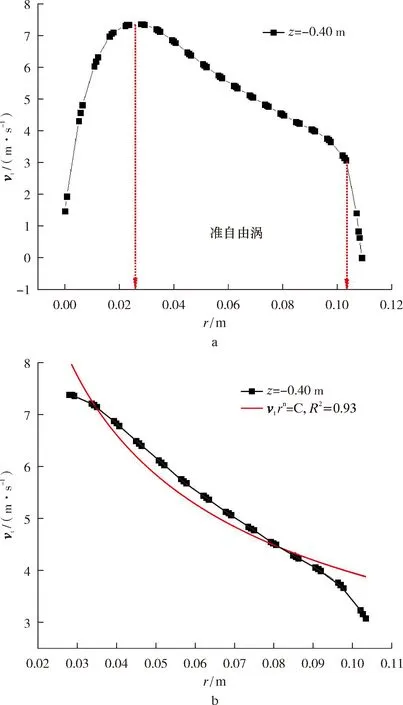
圖5 準自由渦運動的速度分布特征

vtr0.557=1.1

(2)

在旋流器分離過程中，壓力降由組合渦的半自由渦域壓力降Δp和強制渦域的壓力降Δpc兩部分組成，根據伯努利方程，對流體微元進行微分變形后可得：

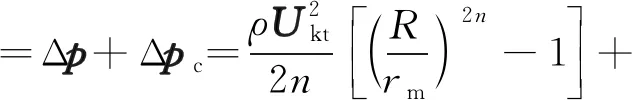
(3)

當rc=0時，從器壁到軸心的最大壓力降為：

(4)

由上可知，rm=0.7ro，且旋流器結構參數R/ro>1，忽略式(4)中方括號中的1，計算結果影響較小。根據調研，吉岡直哉的速度降低系數經驗式應用效果較好，壁邊速度Ukt和最大切向速度Umt分別為：

(5)

(6)

由上可知，n=0.557，將其和式(5)、式(6)代入式(4)，經整理后可得：

(7)

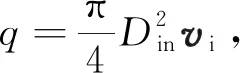
(8)

式中：D、Do分別為筒體直徑和溢流管直徑，mm；Din為入口直徑，mm；vi為入口流速，m/s；Δpm為實際最大壓力降，Pa；ρ為入口混合流體密度，kg/m3。

由式(8)可知，處理量與筒體直徑D、結構參數Din和Do、實際最大壓力降Δpm和入口流體混合密度ρ有關。結構參數Din和Do通常用筒體直徑D的倍數表示，入口流體混合密度ρ與入口含砂體積分數αs有關，即ρ=ρw(1-αs)+ρsαs(ρw為水的密度，ρs為砂的密度)。令Din=C1D、Do=C2D，代入式(8)可得處理量的近似公式：

(9)

由式(9)可知，不同結構的旋流器處理量與筒體直徑的關系不同，但從定性角度可以看出，處理量與筒體直徑平方成正比，與實際最大壓力降的0.5次冪成正比，與含砂體積分數成反比，這可為建立筒體直徑和處理量的定量關系提供理論支撐。

3.2 基于響應面分析的筒體直徑與處理量關系研究

處理量與筒體直徑的定性關系分析中包含較多簡化和假設，計算精度并不高，此外對分離過程的研究未考慮分離效果的影響，在實際應用中具有較大的局限性。實際回灌處理中壓力降、水砂密度變化較小，因此本文僅考慮入口含砂體積分數，基于響應面分析法研究筒體直徑與處理量的關系。

3.2.1 響應面分析方案

采用Design-Expert軟件進行響應面分析。為了建立處理量、含砂體積分數和筒體直徑之間的關系，試驗分析方案采用Box-Behnken設計。處理量、含砂體積分數和筒體直徑這3個因素變化范圍分別為30～120 m3/h、0.1%～1.0%和150～350 mm，處理量、含砂體積分數和筒體直徑的模擬方案如表3所示。

3.2.2 響應面分析結果

按照表3進行數值模擬研究，模擬結果如圖6所示。從圖6可知，處理量、含砂體積分數和筒體直徑對分離效率和壓降的影響較大，分離效率E波動范圍為55%～100%，壓降波動在幾兆帕之內。不同處理量、含砂體積分數和筒體直徑組合對旋流器性能會產生不同的影響，采用響應面分析可以準確把握這種變化趨勢。分離效率較低的模擬案例對應的壓降較高，說明此案例的旋流器結構與入口條件不匹配。

圖6 處理量、含砂質量分數和筒體直徑對分離效率和壓降的影響

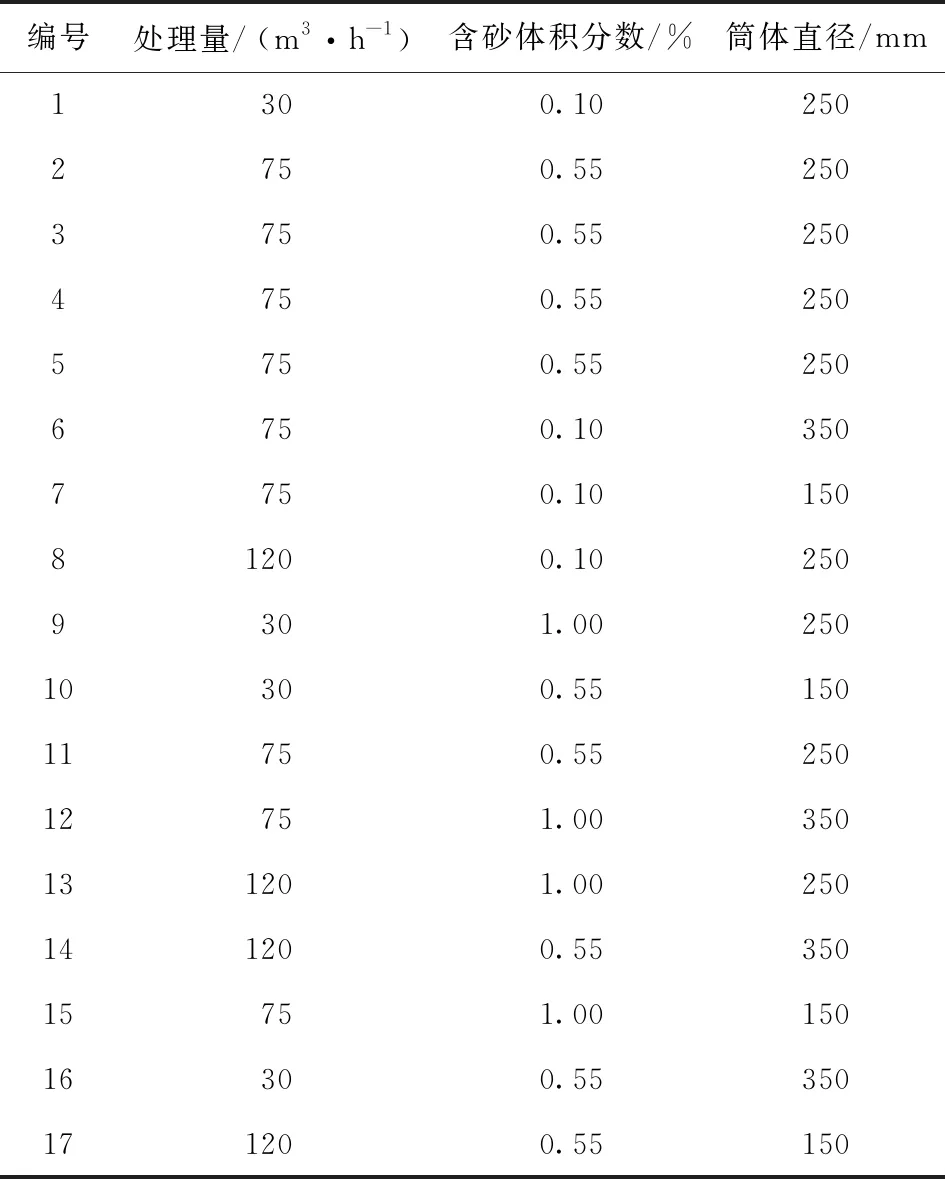
表3 響應面優化方案

3.2.3 響應面分析

選擇二次多項式回歸方程，通過F檢驗某因素水平改變對試驗結果是否有顯著影響，顯著性水平小于0.05時說明影響顯著，具體的方差分析表如圖7所示。

圖7中P-value越小，說明因素對試驗結果的作用越顯著。由圖7可知，與分離效率相關的線性項中，筒體直徑的影響最顯著，其次為處理量，而含砂體積分數影響最小。二次項中，處理量的影響最顯著，其次為筒體直徑，而含砂體積分數影響最小，此外因素間的交互作用均不顯著。得出的二次多項式模型的相關系數R2為0.968 5，但預計的R2僅為0.495 2，二者差值大于0.2。這表示模型可能存在問題，需要對模型進行簡化。

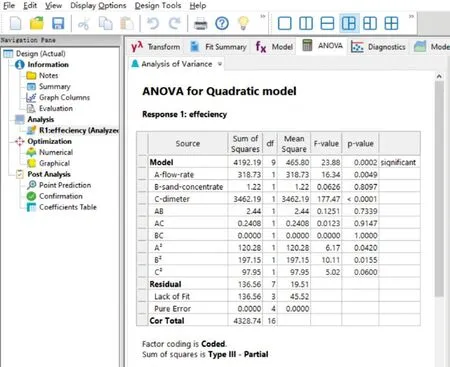
圖7 方差分析表

由于因素的二次項不太顯著，各因素間交互作用均不顯著，故分別選用線性關系(Linear)和修正的二次項關系(Reduced Quadratic)進行回歸分析，其中自定義關系是在二次多項式的基礎上去除各因素間交互作用，即AB、AC和BC項。方差分析結果如圖8所示。

從圖8可知，兩種模型的相關系數R2分別為0.873 7和0.967 8，且預計的R2分別為0.844 6和0.948 5，與相關系數的差值均小于0.2。說明這兩個模型都能夠準確地表征處理量、含砂體積分數和筒體直徑之間的關系，但修正的二次模型的相關系數更高，故選用修正的二次模型作為方差分析模型。由圖8可知，與分離效率相關的線性項中，筒體直徑的影響最為顯著，其次為處理量，而含砂體積分數影響最小。二次項中，含砂體積分數的影響最為顯著，其次為處理量和筒體直徑。

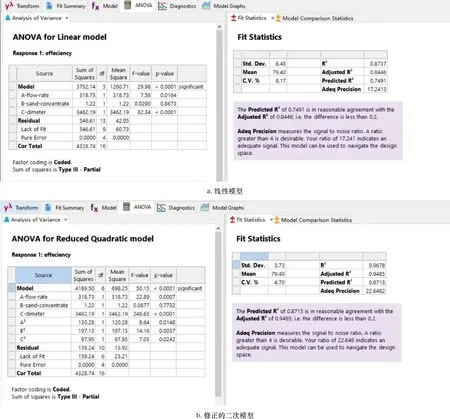
圖8 不同模型下的方差分析

通過方差分析建立修正的二次多項式模型：

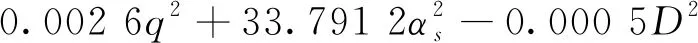
(10)

由于式(10)僅為二次多項式方程，所以計算得到的分離效率存在大于100%的情況，均按100%處理，即此時可完全分離。

3.2.4 模型驗證

為了驗證式(10)經驗關系的準確性，進行室內試驗。試驗系統由水砂混合系統、動力系統、測量系統以及旋流器樣機組成。旋流器室內試驗的流程(見圖9)如下：水通過離心泵經質量流量計進入攪拌罐，砂通過電子天平稱量后加入攪拌罐，水和砂在攪拌罐中混合，實現水砂先分相計量后混合。液固攪拌罐中，通過調節變頻器控制攪拌頻率，在罐內液固兩相混合均勻后經過離心泵增壓，進入到電磁流量計計量，最終到除砂器。在旋流作用下，部分砂粒在流體作用下從溢流口被攜帶出除砂器，部分砂粒因為慣性力和重力的作用成功從多相流中分離，并最終沉積到儲砂筒內。完成一組試驗后，對儲砂筒內砂粒和被攜帶出除砂器的砂粒進行收集、抽濾、烘干、計量，儲存在樣品袋內，以便后續計算分離效率。為確保試驗的準確性，減小操作誤差帶來的影響，每組試驗重復3次。

圖9 試驗流程圖

試驗中除砂器分離效率Es的定義為：

(11)

式中：min為儲砂筒捕集到的砂粒質量，kg；mout為除砂器出口攜帶出的砂粒質量，kg。

以密度2 600 kg/m3的白色石英砂作為固相，液相采用清水。清水在20 ℃、0.1 MPa 工況下的密度為998.2 kg/m3，運動黏度為1.007 mPa·s。

由于室內試驗流量限制，選取4種不同處理量進行試驗，分別為0.4、1.3、2.6和3.9 m3/h，對應表觀流速分別為0.02、0.08、0.16和0.25 m/s，試驗所獲分離效率與經驗公式(10)計算的分離效率如表4所示。

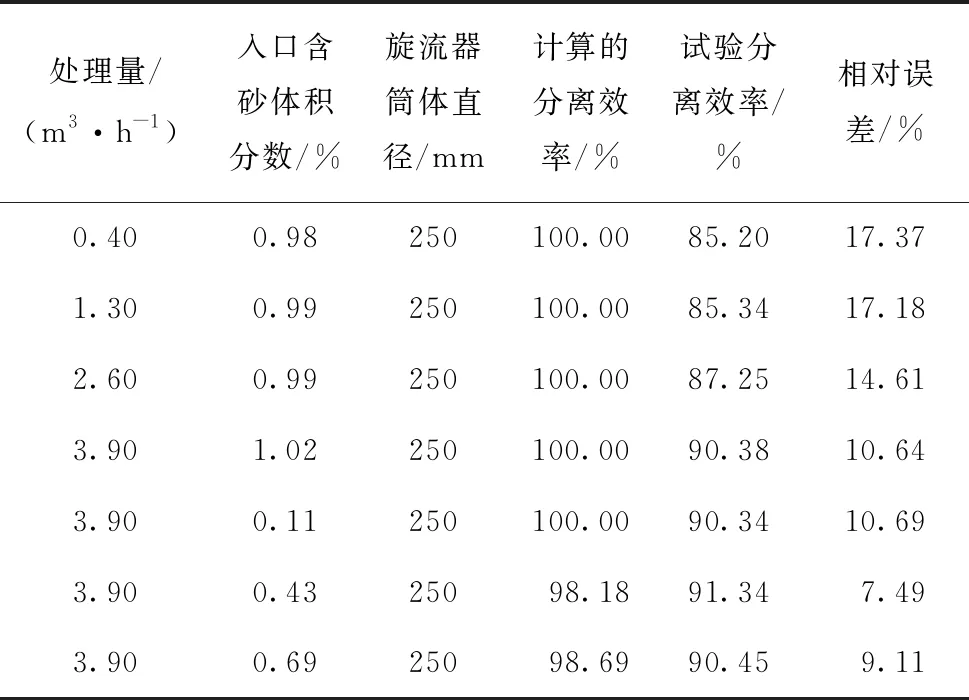
表4 分離效率試驗結果與公式計算結果對比

從表4可知，計算的分離效率與試驗分離效率比較接近，相對誤差在18%以內，滿足工程要求。誤差較大的原因是室內試驗中處理量均較低(小于3.9 m3/h)，與響應面分析中處理量范圍(30～120 m3/h)差距較大，故還應進一步開展現場試驗。綜上，式(10)可以較為準確地描述處理量、含砂體積分數和筒體直徑之間的關系。

4 結 論

(1)旋流器處理量與筒體直徑的平方和實際最大壓力降的0.5次冪成正比，與含砂體積分數成反比。

(2)分離效率的影響因素中，筒體直徑的影響最顯著，其次為處理量，含砂體積分數影響最小。二次項中，含砂體積分數的影響最顯著，其次為處理量和筒體直徑。

(3)建立了旋流器處理量、筒體直徑和含砂體積分數的經驗公式，經室內試驗驗證，在低處理量下，模型相對誤差在18%以內，滿足工程要求。