基于改進灰狼優化算法應力強度因子預測模型

潘海珠，葛海淼，蘇小紅，袁 琪

（1.齊齊哈爾大學計算機與控制工程學院，黑龍江齊齊哈爾 161006；2.哈爾濱工業大學計算機科學與技術學院，哈爾濱150001）

0 引言

由功能梯度材料（Functionally Graded Material，FGM）制備的受力部件在循環應力或應變作用下會產生局部結構變化，形成疲勞裂紋并產生擴展，對構件及工程安全構成嚴重威脅。裂紋尖端的應力場強度，即應力強度因子（Stress Intensity Factor，SIF），是表征材料斷裂的重要參量，它和材料屬性、應力大小和裂紋幾何尺寸等因素密切相關。由于FGM 屬性呈現梯度變化，使得傳統的理論解析求解方法較難求解裂紋問題。隨著信息技術不斷發展，許多學者嘗試運用人工智能方法與傳統理論求解模型相結合，來解決復雜的斷裂問題［1-5］。其中，支持向量回歸（Support Vector Regression，SVR）是支持向量機（Support Vector Machine，SVM）在解決回歸和預測問題中的擴展［6］，作為一種高效的機器學習方法，采用最小化經驗誤差和最大化幾何邊緣策略，常用來解決小樣本、非線性問題。但是，SVR 方法在內核參數選擇上存在一定困難，易使模型陷入局部最優，文獻［7-12］中提出了基于SVR的改進算法進行參數優化，可提高預測模型的準確性和魯棒性。改進的SVR 預測模型研究可以作為傳統斷裂力學研究的新手段，用于快速得到力學本構模型和控制方程的函數表達形式。基于概率變異灰狼優化算法的SVR是支持向量回歸的一種改進類型，通過變異的灰狼優化算法對SVR 的幾個主要參數進行優化，實現小樣本情況下的SIFs預測。

本文以含有任意方向裂紋的一般屬性FGM 為研究對象，分析應力強度因子與FGM屬性、裂紋長度、裂紋角度等的關系，提出了SVR結合概率變異的灰狼優化算法（Probability Mutation Grey Wolf Optimization Algorithm，MP-GWO），通過優化SVR 參數，運用分層指數模型方法獲取數據，訓練一個以裂紋幾何參數及FGM屬性等特征值為輸入，應力強度因子為輸出的預測模型。在傳統力學建模方法獲取數據基礎上，提出一種新的基于機器學習方法的斷裂力學預測模型，并通過有效實驗驗證該模型的適用性和精確性。本文的目的在于運用分層指數模型獲取離散應力強度因子，訓練一個支持向量回歸模型，提出了概率變異灰狼優化（MP-GWO）算法對模型參數進行優化，將這些離散應力強度因子在高維空間擬合成一個超平面，實現了運用機器學習方法擬合出隱式的本構關系，對不同材料參數及裂紋幾何參數條件下的SIFs預測；對比傳統的灰狼優化算法，提出的改進算法，即基于MP-GWO算法的支持向量回歸模型能更好抑制算法陷入局部最優，得到的應力強度因子預測模型泛化能力更優。

1 MP-GWO-SVR原理

1.1 SVR基本原理

設樣本集｛（xi，yi），i=1，2，…，n｝，其中，xi∈RD為數據樣本的輸入值；yi∈R為樣本的輸出值；D為樣本維度。對于非線性的SVR問題，可以引入映射函數φ（·），將輸入數據映射到高維特征空間F中，定義回歸預測模型

式中：w 為權重向量；b為常數；f（x）為回歸預測模型輸出。引入松弛變量（，ξi），定義f（xi）與yi的損失函數

式中：C是懲罰因子；ε 是最大允許誤差。目標函數為最小化損失函數J，引入拉格朗日乘數及核函數可以將目標函數轉化為如下對偶形式：

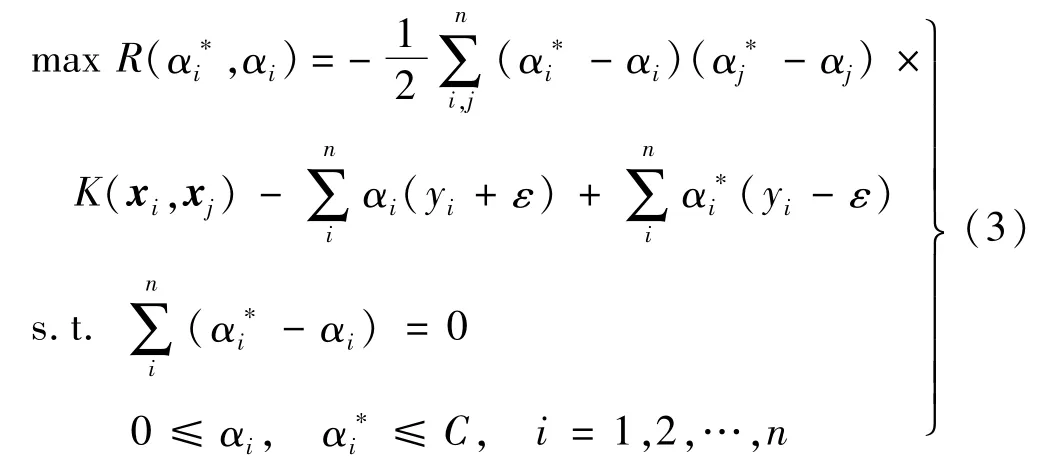
式中：αi和為拉格朗日乘數；K（xi，xj）=φ（xi）φ（xj）為核函數，定義徑向基核函數

式中，σ為內核參數［7］。通過求得的αi和，可以得到SVR表達式

式中：xr和xs是任意的支持向量；SVs 為支持向量的數量。

在SVR 應用中，參數懲罰因子C、RBF 核函數參數σ 和最大允許誤差ε 對模型的學習能力和泛化能力有重要影響，因此對這些參數進行優化尤為重要，本文提出使用MP-GWO算法優化SVR的3 個參數。

1.2 概率變異灰狼優化（MP-GWO）算法

（1）灰狼優化（Grey Wolf Optimization，GWO）算法。GWO算法［13］是一種模擬狼群狩獵行為的群體智能優化算法。GWO 算法在搜索空間隨機產生灰狼種群，將狼群劃分為不同等級的α 狼、β 狼和γ 狼，剩余個體為ω狼；通過包圍獵物、攻擊獵物行為實現對目標獵物的獵殺，獲得待優化問題的最優解。

GWO的包圍行為首先確定灰狼與獵物之間的距離，更新灰狼的位置，其數學表達式如下：

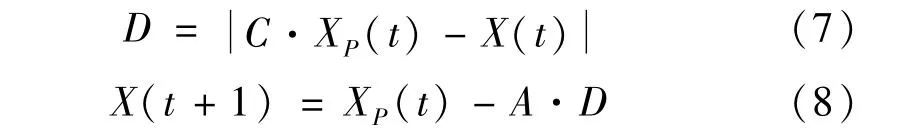
式中：t表示當前的迭代次數；D表示灰狼與獵物的距離；XP（t）為第t代獵物的位置；X（t）為第t代單只灰狼的位置向量；A和C為隨機常系數，

r1和r2為［0，1］間的隨機數；數值ɑ隨迭代次數增加從2 遞減至0，表達式為

l為當前迭代次數；nmax為最大迭代次數。

GWO的狩獵行為在α狼、β狼和γ 狼的領導下進行，其數學表達式為：

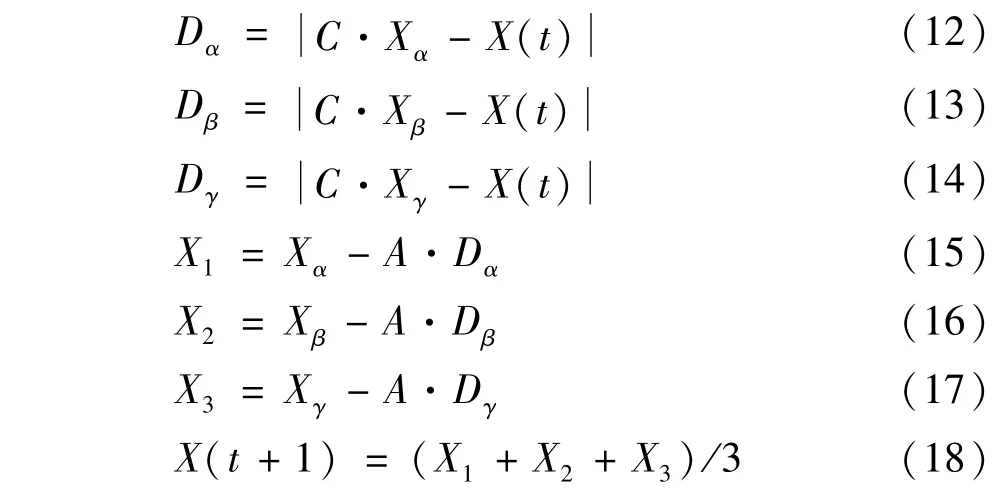
式中：Xα、Xβ、Xγ分別為頭狼α 狼、β 狼和γ 狼位置；Dα、Dβ、Dγ分別為狼群剩余個體ω狼與α狼、β 狼和γ狼的距離；X1、X2、X3分別用于計算3 個頭狼的運動軌跡；X（t+1）為灰狼更新后的位置。GWO 算法通過迭代過程更新狼群位置，逐漸逼近獵物，完成對獵物的捕食。

GWO算法的全局搜索能力體現在隨機數A和C，但該算法在初始化群體時就傾向于搜索可能存在的最優解，這種搜索策略易導致結果局部最優［14-17］。為改進GWO算法的全局搜索能力，并進一步增強算法的魯棒性，本文提出一種變異策略的灰狼尋優算法。

（2）MP-GWO 算法。MP-GWO 算法在生成狼群位置X（t+1）后，以遞減概率對狼群位置進行變異計算。變異計算分為兩種，分別為交叉變異和普通變異。狼群中的個體根據變異概率產生某一種變異。

交叉變異根據當前最優解Xα和當前狼的位置X（t+1）決定ω狼的位置，交叉變異具體表達式如下：

式中：r3，r5為［0，1］間的隨機數；Mp為變異概率閾值。

普通變異根據當前狼位置X（t+1）和搜索空間范圍決定ω狼的位置，普通變異的表達式如下：

式中：r4為［0，1］間的隨機數；ub和lb分別為搜索空間上下界。式（19）、（20）限制條件中的隨機數r5用于控制交叉變異或普通變異是否發生。

為保證狼群個體只能產生一種變異，變異概率閾值為［0，0.5］之間的值。為保證算法收斂，變異概率閾值應隨迭代次數增加而減小，變異概率閾值Mp表達式如下

式中：p為變異概率常數，為［0，0.5］間的值。

MP-GWO算法的具體步驟如下：

（1）初始化GWO算法的參數。狼群中狼的數量Nw，變異概率常數p，搜索空間上下限ub和lb，搜索空間維度D，最大迭代次數nmax。

（2）計算灰狼個體的適應度，根據適應度值的大小進行排序，前3 名灰狼位置設置為Xα，Xβ，Xγ。

（3）根據式（9）～（11）、（21）更新A，C，ɑ，Mp的值。

（4）遍歷每個狼個體，根據式（12）～（18）更新狼的當前位置；當r5∈［0，Mp］，其中r5為［0，1］間隨機數，根據式（19）計算當前狼位置的交叉變異值，更新位置；當r5∈［MP，2MP］，根據式（20）計算當前狼位置的普通變異值，更新位置。

（5）判斷每一個狼個體的位置是否超出搜索空間上下限ub和lb，如位置值大于ub，則將當前狼位置值設為ub；如位置值小于lb，則將當前狼位置值設為lb。

（6）判斷是否達到最大迭代次數，若達到則跳出算法，輸出最優值Xα；否則，設置l=l+1，跳轉到步驟（2）。

2 應力強度因子計算

圖1 為含有任意方向裂紋具有一般材料屬性功能梯度材料示意圖。材料無限長且厚度為l，所含裂紋與材料梯度變化方向的角度為α。如圖1 所示，在x′Oy′坐標系下，裂紋兩個端點坐標分別為（ɑ，0），（b，0）。由于任意屬性FGM的裂紋問題難于解析求解，采用分層指數模型來求解一般材料屬性FGM斷裂問題，假設FGM實際屬性可以用指數函數、線性函數、冪函數等一般連續性函數來描述［18］。充分利用指數型材料的控制偏微分方程易求解這一特點，通過傅里葉變換、微分算子等方法求解應力場和位移場；結合裂紋問題的邊界條件和位移條件，求解奇異積分方程組，求得混合型應力強度因子k值如下：

圖1 含任意方向裂紋的功能梯度材料示意圖

式中：κ、δ 為材料參數；n為分層指數模型劃分的層數；f1、f2為求解奇異方程組引入的可求解函數。運用該方法求得的應力強度因子用于訓練SVR預測模型。

3 MP-GWO-SVR應力強度因子預測模型

由于SVR的性能主要受懲罰因子C、RBF核函數參數σ和最大允許誤差ε影響，使用MP-GWO算法實現對SVR 3 個參數進行優化。生成的SIFs 預測模型計算步驟如下：

（1）樣本數據初始化。材料屬性變化形式、模量比、裂紋相對長度和裂紋角度為輸入值，裂紋尖端應力強度因子為輸出值，組成樣本集和標簽集（Sample_all，label_all）。考慮3 種材料屬性變化形式，即材料屬性變化分別用指數函數、線性函數和冪函數來描述；材料上下表面彈性模量比取值為（2，2.5，3，4，5）；裂紋相對長度的取值為（0.1，0.15，0.2，0.25，0.3，0.35，0.4，0.45，0.5）；裂紋角度的取值為（0π，0.05π，0.1π，0.15π，0.2π，0.25π，0.3π，0.35π，0.4π，0.45π，0.5π）；樣本總數為202 個；隨機選擇1/2 樣本作為訓練樣本（Sample_train），共101 個樣本，其標簽為label_train，其他樣本作為測試樣本（Sample_test），共101 個樣本。

（2）參數初始化。初始化狼群數量Nw=10，其中頭狼α、β和γ占狼群數量為3，剩余個體ω 狼占狼群數量為7；變異概率常數p=0.5；搜索空間上下限ub=［100，100，0.2］和lb=［0.01，0.01，0.001］；搜索空間維度D=3；nmax=10。

（3）使用Sample_train 訓練SVR，使用MP-GWO算法尋找SVR的最佳參數C、σ和ε。

（4）使用C、σ 和ε 實現SVR 的建模，得到SVR模型model_SVR。

（5）使用model_SVR預測Sample_test的值，得到測試樣本的預測值label_test_SVR。

4 實驗結果及分析

以冪函數表征材料屬性變化形式，材料上下表面彈性模量比值為2.5 的特征數據為例，將SVR模型預測結果，即無量綱化應力強度因子kI（ɑ）、kI（b）、kII（ɑ）和kII（b）分別標注為Label1、Label2、Label3和Label4，圖2～5 分別給出不同裂紋參數下MP-GWOSVR模型與GWO-SVR模型的SIFs預測值，以及運用分層法求解SIFs（真實值）的變化曲線。

圖2 基于GWO-SVR的SIFs預測模型預測結果

對比圖2（a）和圖4（a）可以看到，對于不同長度的裂紋，當裂紋角度較大時（如0.4π，0.45π，0.5π），應力強度因子kI（ɑ）較真實值有較大的差別。比較圖3（a）和圖4（a），可以看到MP-GWO-SVR 模型預測SIFs曲線較分層模型求解SIFs 曲線變化趨勢相似度都很高；尤其注意到當裂紋角度較大時（如0.4π，0.45π，0.5π），兩種模型給出曲線的變化趨勢幾乎一致。這種現象說明MP-GWO-SVR 模型較GWO-SVR模型在Label1上有更好的擬合度。對比圖2（b）、圖3（b）和圖4（b），可以看到MP-GWO-SVR 模型得到了與分層模型求解SIFs曲線相似度很高的擬合曲線，而GWO-SVR模型對于裂紋角度較大時預測結果與真實值偏離較大，這種現象說明MP-GWO-SVR 模型在Label2上可得到較為理想的擬合結果。對比圖2（c）、圖3（c）和圖4（c），可以看到情況有所不同。在裂紋相對長度為0.1 和0.2 時，GWO-SVR 和MP-GWOSVR兩種模型預測SIFs曲線都有變形，但是從圖中可以看到，MP-GWO-SVR模型的預測曲線變形程度明顯小于GWO-SVR 模型；當裂紋相對長度為0.3 時，GWO-SVR模型和MP-GWO-SVR 模型給出的SIFs 預測曲線擬合度較高；當裂紋相對長度為0.4 和0.5 時，GWO-SVR模型的SIFs預測值隨裂紋角度變化出現明顯波動，相比真實值曲線有明顯的變形，而MP-GWOSVR模型的SIFs預測曲線與分層模型求解SIFs 曲線形狀基本一致。這種情況說明對Label3，GWO-SVR和MP-GWO-SVR模型對SIFs 擬合結果都有的誤差，但MP-GWO-SVR模型的預測誤差相對較小。對比圖2（d）、圖3（d）和圖4（d），可以看到GWO-SVR 模型給出的SIFs擬合曲線較分層模型求解SIFs 曲線有較明顯的變形，而MP-GWO-SVR模型給出的擬合曲線較分層模型求解SIFs曲線擬合度很高，說明MP-GWO-SVR模型在Label4上擬合能力優于GWO-SVR模型。以上分析結果與圖5 中的SIFs樣本點對比結果一致。

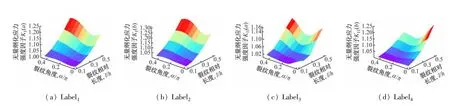
圖3 基于MP-GWO-SVR的SIFs預測模型預測結果

圖4 分層模型求解SIFs

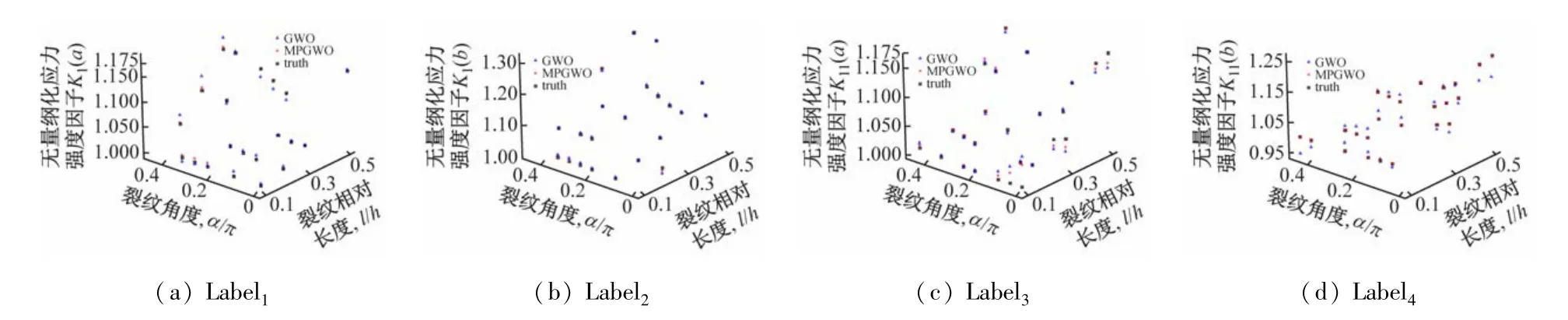
圖5 GWO-SVR、MP-GWO-SVR預測值與真實值作對比

為了進一步比較MP-GWO算法和GWO算法的性能，本文采用均方誤差（Mean Square Error，MSE）和誤差范圍百分比（Percentage of Error Range，PER）兩種度量標準分別對基于兩種算法的SVR 生成SIFs 預測模型進行預測精度評價，其定義如下：

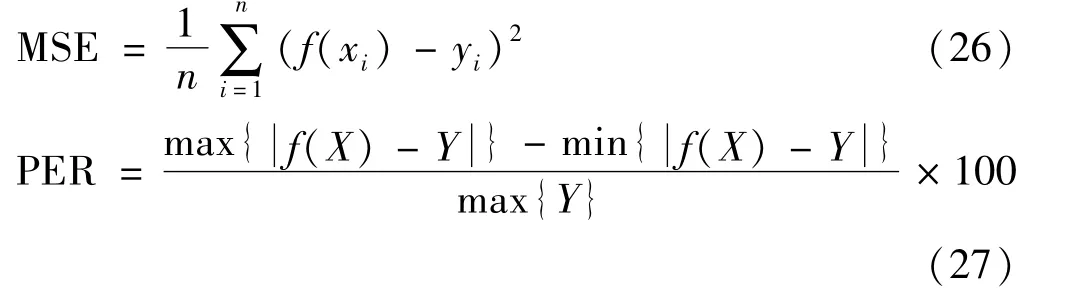
式中：n為樣本數；f（xi）為樣本的預測值；yi為樣本的真實值（即運用分層模型得到的解）；f（X）為預測值向量；Y為真實值向量；max｛·｝為求目標集合的最大值；min｛·｝為求目標集合的最小值。

選取其中兩組數據為例，分別計算其均方誤差及誤差范圍百分比，結果如表1、2 所示。由表1 可見，基于算法GWO 的SVR 模型在Label1、Label2、Label3和Label4上的均方誤差在4.583 5 ×10-4～3.939 1 ×10-5之間，其中Label1和Label2的均方誤差較小，Label3和Label4的均方誤差較大；基于算法MP-GWO的SVR模型在各標簽上的均方誤差范圍為7.556 2 ×10-5～5.364 4 ×10-6，其中Label1的均方誤差較小，Label2、Label3和Label4的均方誤差較大。對比算法GWO和MP-GWO，可以看到MP-GWO-SVR 模型的均方誤差在各個Label 上都小于GWO-SVR 模型。這種現象說明MP-GWO 算法構建的預測模型有較高的泛化能力。從表2 可以看到，基于算法MP-GWO的SVR模型在Label1、Label2和Label3上的誤差范圍都小于GWO-SVR模型，兩者在Label4上有相似的誤差范圍。這種現象表明，MP-GWO 算法較GWO 算法相比，其SVR模型不易出現偏離實際值過大的預測值，有更好的穩定性。

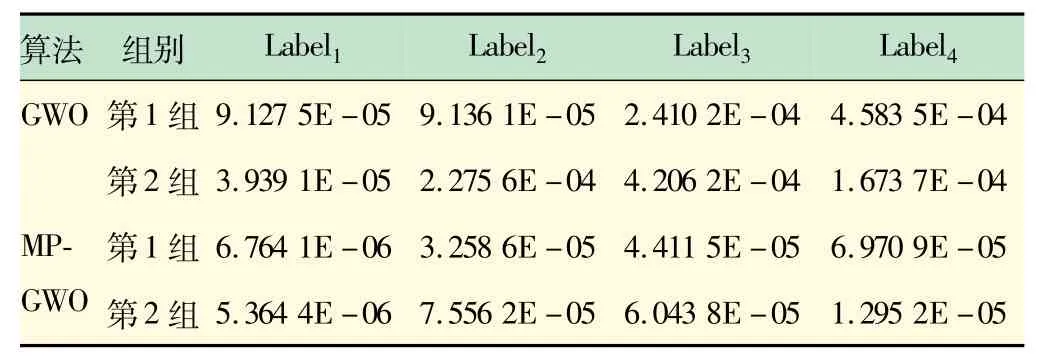
表1 兩種算法構建預測模型的均方誤差對比

表2 兩種算法構建預測模型的誤差范圍對比 %

5 結語

本文以含任意方向裂紋的功能梯度材料斷裂問題為研究對象，運用機器學習方法，用小樣本數據訓練一個支持向量回歸模型，實現對含有任意方向裂紋的一般屬性功能梯度材料應力強度因子的預測分析。本文在傳統的基于灰狼優化算法的SVR 模型基礎上提出了一種改進算法，即概率變異灰狼優化算法，構建SVR模型預測SIFs。該算法優化SVR參數，獲取模型的預測精度比基于傳統灰狼優化算法支持的預測模型有顯著提高，從得到的誤差范圍來看，概率變異灰狼優化算法SVR預測模型的預測結果與樣本數據的擬合度更好。本文在傳統斷裂力學研究方法基礎上運用智能優化算法，為斷裂力學問題研究提供了一種可擴展的研究模式，該方法將在今后的斷裂力學理論與實驗研究中將發揮重大作用。

·名人名言·

對真理的追求要比對真理的占有更可貴。

——愛因斯坦