考慮LMP的城市電動汽車充電站優化配置

文家利，劉友波，黃 媛，向 月

（四川大學電氣工程學院，成都 610065）

0 引言

近年來，隨著電池技術取得了重大突破，同時響應國家“綠色發展”戰略，各大汽車制造商重點打造新能源汽車產業，尤其是純電動汽車［1］。然而，城市充電服務網絡的不完善制約著電動汽車的發展，電動汽車充電負荷大量接入配電系統也會造成配電系統出現阻塞現象，不僅對電網公司造成經濟損失，而且會影響企業投資者的決策。充電配套服務不僅對電動汽車制造企業很重要，對電動汽車用戶更加重要。消費者購買電動汽車時會重點考慮充電問題，而企業在推廣電動汽車時若沒有配套充電設施，消費者會退縮，會阻礙電動汽車的普及。隨著國家政策出臺，越來越多的企業開始投資電動汽車充電站［2］，綜合多維信息進行電動汽車充電站規劃是投資者亟需解決的問題。

目前，國內外研究學者對電動汽車充電負荷預測和充電設施規劃進行了大量研究，其中文獻［3］中建立了以投資成本為目標函數，重點考慮交通信息作為約束條件，并用量子粒子群算法進行求解。文獻［4-5］中以電動出租車為對象，充分研究其運行特性，分別以總耗時和總耗時費用為目標函數，建立了電動汽車充電設施優化配置模型。文獻［6］中綜合考慮道路信息、車流信息和配電系統拓撲結構，以電動汽車用戶的損耗成本和充電站線路投資成本之和為目標函數，并考慮配電系統容量約束，構建了充電站的選址定容模型。文獻［7］中從社會企業角度出發，研究了社會企業投資電動汽車充電站規劃時應考慮的因素，運用雙層規劃理論建立了電動汽車充電站優化配置模型，能實現社會投資者和電動汽車用戶各自利益的有效折中。文獻［8］中將城市規劃區域劃分為多個正方形區塊，以總投資費用最小為目標函數建立了充電設施規劃模型，約束條件包括服務半徑、充電容量等。文獻［9］中提出了一種兩步優化選址模型，先利用免疫算法獲得規劃區域內充電站待選點，后利用模糊層次分析法進行綜合量化并確定最有選址。上述研究成果對電動汽車充電站的規劃具有重要的指導意義，而在電力市場環境下電動汽車大量接入電網引起電網阻塞問題等方面鮮有研究，在規劃中進行重點考慮具有重要的工程價值。

基于上述背景，本文提出一種考慮配電系統接入大量電動汽車充電負荷后出現輸電阻塞情況時的城市電動汽車充電站優化配置模型。該模型由上層決策模型和下層決策模型組成，上層模型以電動汽車制造企業的投資收益最大化為目標，考慮電網潮流、儲能系統充放電和投資預算等約束條件；下層模型以電動汽車用戶的滿意程度最大化為目標，考慮用戶選擇充電站和充電站必須存在約束條件，并采用改進遺傳算法對模型進行求解，進而確定充電站的最優規劃方案。

1 電動汽車充電負荷計算

電動汽車充電負荷計算是概率性問題，將電池初始SOC與初始充電時刻、用戶出行與駕駛習慣和充電電價等因素綜合分析，可建立精確的電動汽車充電負荷計算模型，這是電動汽車充電設施網絡建設的前提。本文主要考慮電動公交車、電動客車、電動出租車（網約車）和電動私家車，由于各類電動汽車出行規律各異，根據文獻［8，10］中將電動公交車和客車歸為一類，電動公交車、電動客車和電動出租車的日行駛距離滿足正態分布［11］，電動私家車日行駛距離滿足對數正態分布［3］，具體為：

式中：s表示電動汽車的日行駛距離；μ1和σ1表示電動公交車、電動客車與電動出租車的日行駛距離期望和標準差；μ2和σ2表示電動私家車的日行駛距離期望和標準差。

不同類型電動汽車的日行駛距離與充電時刻與用戶的出行習慣息息相關，本文采用文獻［12］中擬合結果描述電動汽車初始充電時刻的概率密度函數，即

式中：tb為電動汽車初始充電時刻；μ3和σ3分別為開始充電時刻的期望和標準差。

電動汽車充電時長與日行駛距離有關［12］，即

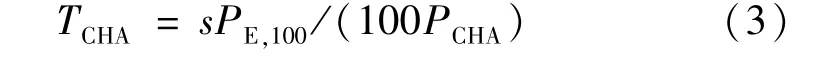
式中：PE，100為電動汽車行駛100 km 的耗電量；PCHA為充電功率。

2 節點邊際電價模型

2.1 數學模型

LMP定義為電力系統實時運行狀態下，某個節點負荷增加單位有功功率，并滿足電網運行安全約束時系統邊際成本［13］。在電力市場中，LMP表征了不同節點在不同時刻的電能價值，反映了電能的稀缺程度。

基于交流最優潮流的LMP模型，能精確反映電網的網絡損耗和電網阻塞情況。交流最優潮流模型通常是以全網發電機組發電成本最小為目標函數，具體表達式為

式中：N表示全網節點數量；ɑi、bi和ci分別表示節點i處發電機組的發電成本函數系數。

需滿足的約束條件包括節點功率平衡和線路潮流不越限，具體表達式為

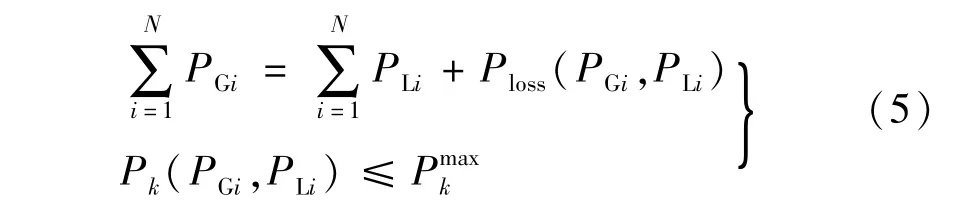
式中：PLi和Ploss分別表示節點i的負荷有功功率和系統網絡損耗；Pk和分別表示線路k的實際有功功率和有功功率最大值。

2.2 含電動汽車充電站的節點邊際電價模型

電動汽車充電站通過節點接入配網，在功率平衡等式約束條件中加入充電負荷變量PCi即可構成含電動汽車充電站的節點邊際電價模型。將目標函數和約束條件形成拉格朗日函數L，具體表達式為

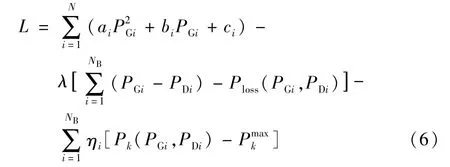
式中：PDi表示節點i處接入充電站后的節點負荷有功功率，PDi=PLi+PCi；λ 和η 分別表示各約束條件對應的拉格朗日乘子。

根據KKT一階最優條件，即可求得節點i處的節點邊際電價的表達式為

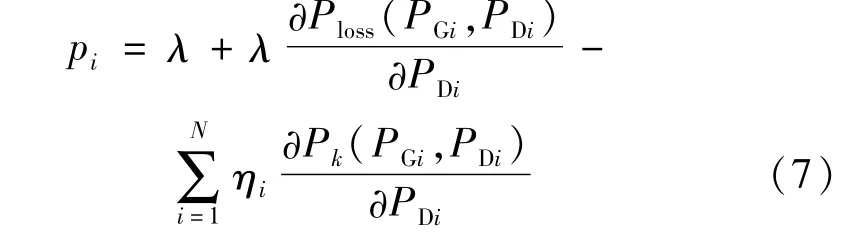
由式（7）可知，LMP是一個非線性函數，由能量價格分量、網絡損耗分量和線路阻塞分量構成。當電網不發生網絡阻塞時線路阻塞分量為零。因此，在進行電動汽車充電站規劃設計時需重點考慮。

3 充電站雙層規劃模型及求解

電動汽車生產企業（如特斯拉、蔚來、吉利和比亞迪等）和充電設施制造企業（如特來電、許繼電氣和上海普天等）為增加自家電動汽車或者充電設施的市場占有率，會在城市中構建自己的電動汽車充電服務網絡。本文以電動汽車生產或制造企業為對象進行研究，此類投資者側重于電動汽車充電服務網絡產生的收益和用戶服務滿意度。

3.1 上層規劃模型

隨著電池技術的日益成熟，電動汽車的數量逐年攀升，尤其是一二線城市，未來三四線城市的增長率也會越來越大。因此，上層決策者會根據城市的電動汽車保有量、城市配電系統和城市道路交通網絡等多維度信息，并充分考慮電動汽車充電站的總投資預算、充電容量和電壓安全等約束條件，以充電站的年收益最大為目標建立上層規劃模型，即

式中：CBEN、CINC和CCOS分別表示投資充電站而獲得的總投資收益、總營業收入和總投資成本；r和τ分別表示年利率和充電站運行年限。

（1）總營業收入CINC。總營業收入是指投資者通過運營電動汽車充電站而獲得的總營業收入，主要包括充電營業收入、提高分布式電源設備利用率收益和削峰填谷政府補貼收入，具體表達式為

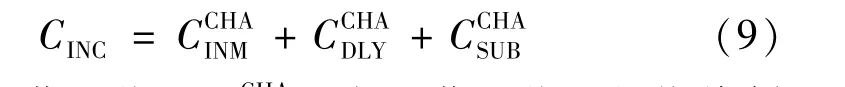
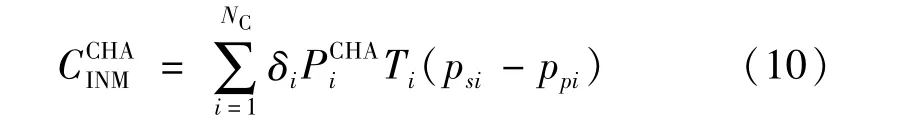
式中：NC表示新建充電站的數量；δi表示節點i處是否建設充電站的二元決策變量，值為1 表示新建，值為0 表示不新建；表示節點i處充電站的規劃充電容量；Ti表示節點i處充電站的年最大利用小時數；psi和ppi分別表示節點i處充電站向充電用戶售電價格和向電力公司購電價格，而購電價格就是前文所述的節點邊際電價。

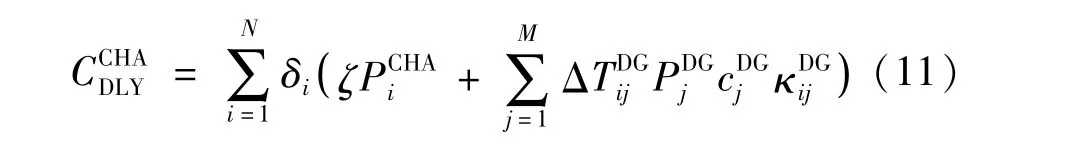
式中：ζ表示單位功率配網擴建成本；M表示配網中分布式電源的數量；表示節點i處電動汽車充電站提高了第j個分布式電源的年利用小時數；表示第j個分布式電源額定功率；表示第j個分布式電源平均套利電價；κ表示節點i處電動汽車充電站與第j個分布式電源投資商的分成比例。

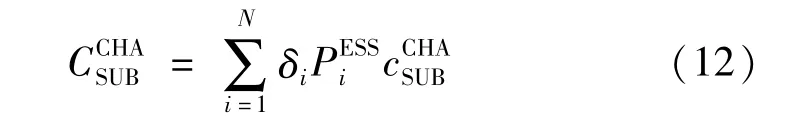
（2）總投資成本CCOS。電動汽車充電站的總投資成本包含充電站的建設與運營成本、財務成本和用戶排隊時間成本。

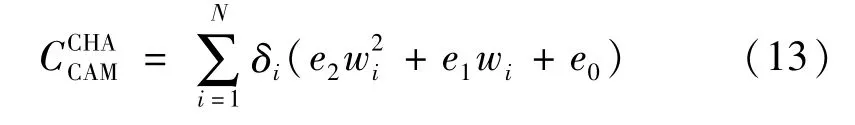
式中：wi為節點i處的充電站內充電機數量；e1和e2分別為充電機單價和與充電機臺數有關的等效投資系數；e0為充電站固定成本。

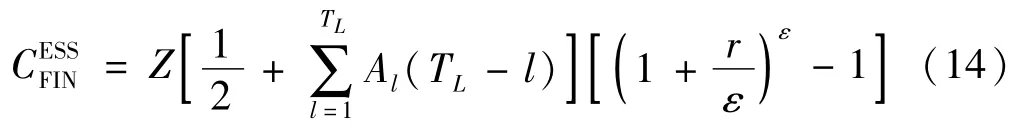
式中：Z表示項目貸款或融資的總額；TL表示充電站項目的建設周期；Al表示第l年的貸款資金使用比例，且滿足；ε表示每年計息次數。

式中：M為充電用戶數量；λmi為第m個用戶選擇節點i處充電站的二元變量，值為1 表示選擇，值為0 表示不選擇；tmi為第m個用戶在節點i處充電站內充電等待時間，用排隊論求得［17］；c0為單位時間成本。

投資者建設充電站的上層規劃模型需要滿足相關約束條件。

（1）所有充電站接入配電系統的總功率應小于配電網允許的最大接入功率，即

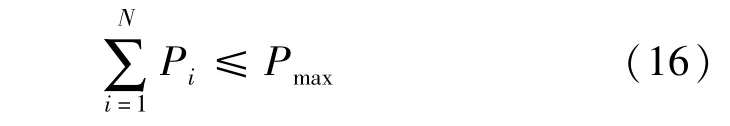
式中，Pmax表示配網允許的最大接入功率。

（2）為保證配電系統的安全穩定運行，充電站接入配網運行后，配網節點的電壓幅值應滿足響應的約束條件，即

式中：Ui表示城市配網節點i處電壓幅值；分別表示節點i處電壓幅值的最小值和最大值。

（3）配網線路極限容量固定，充電站接入配網后應保證饋線電流在規定范圍內，即

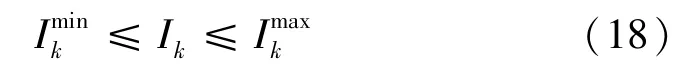
式中：Ik表示實際流過線路k的電流；分別表示流過線路k電流的最小值和最大值。

（4）充電站配置的儲能系統充放電功率應滿足相應約束條件，即

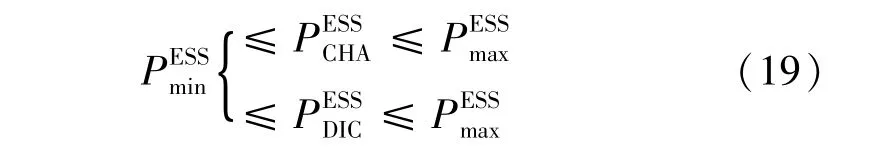
（5）企業投資者在進行項目時，會考慮到項目投資預算，即

式中，CINV表示項目總投資預算。

（6）根據規劃區內電動汽車數量預測，企業投資者會制定新建充電站數量約束，即

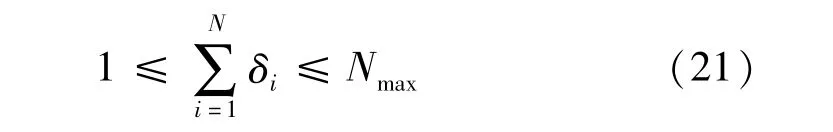
式中，Nmax表示新建數量上限。

3.2 下層規劃模型

投資電動汽車充電站就是讓電動汽車用戶獲得最大的體驗感和滿意度，充電服務時間是決定用戶體驗的關鍵。因此，本文引入效用函數［18］來衡量用戶對充電服務時間的體驗感和滿意度ρ，其具體表達式為

據此，下層規劃模型以用戶體驗感或滿意度最大為目標，具體表達式為

下層模型需要滿足的約束條件如下：

（1）用戶只能選擇一個電動汽車充電站進行充電服務，即需要滿足的約束條件為

（2）第m個用戶選擇節點i處的電動汽車充電站進行充電的前提是節點i處存在充電站，因此，須滿足的約束條件為

3.3 模型求解算法及流程

雙層規劃問題是一個NP-Hard 問題，采用智能算法進行求解可提高運行效率和精度。本文基于遺傳算法［19］并結合所提模型的特點，進行相應改進和校驗，進一步提升模型求解精度。電動汽車充電站雙層規劃模型的求解流程如圖1 所示。

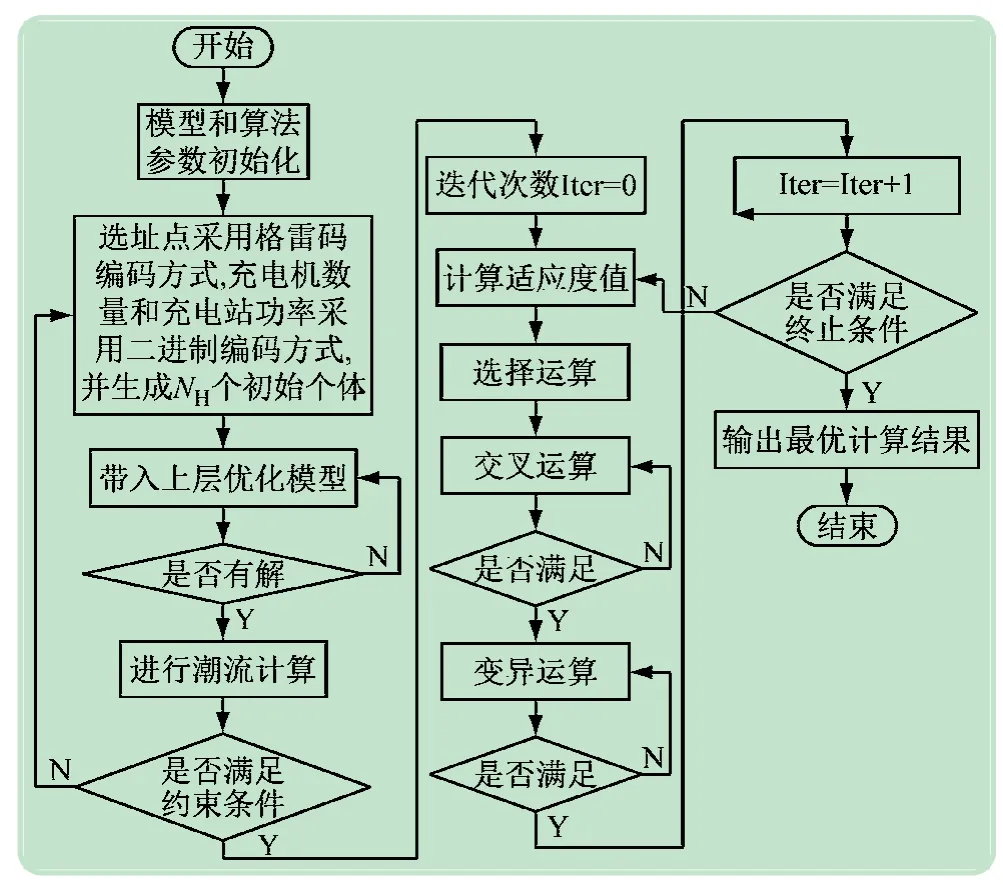
圖1 雙層規劃模型的求解流程

4 算例分析

本文以中國西部某局部配網拓撲為算例，該局部配網覆蓋區域面積約為450 km2，電動汽車保有量預測數據為10 萬輛。該局部配網包括4 條10 kV 線路分別由4 座變電站引出，3 個線路聯絡開關，根據實際道路地理信息，所有電動汽車充電站備選點均位于道路的交叉路口，共計12 個，如圖2 所示。配網中風力機組的額定功率為1.0 MW，光伏發電機組的額定功率為0.75 MW。根據電動汽車保有量和預測模型，該規劃區域內單日充電功率的最大期望值是28.64 MW。某電動汽車制造商根據城市汽車保有量、交通和配網等信息，計劃在該區域內投資新建5～8 座電動汽車充電站。

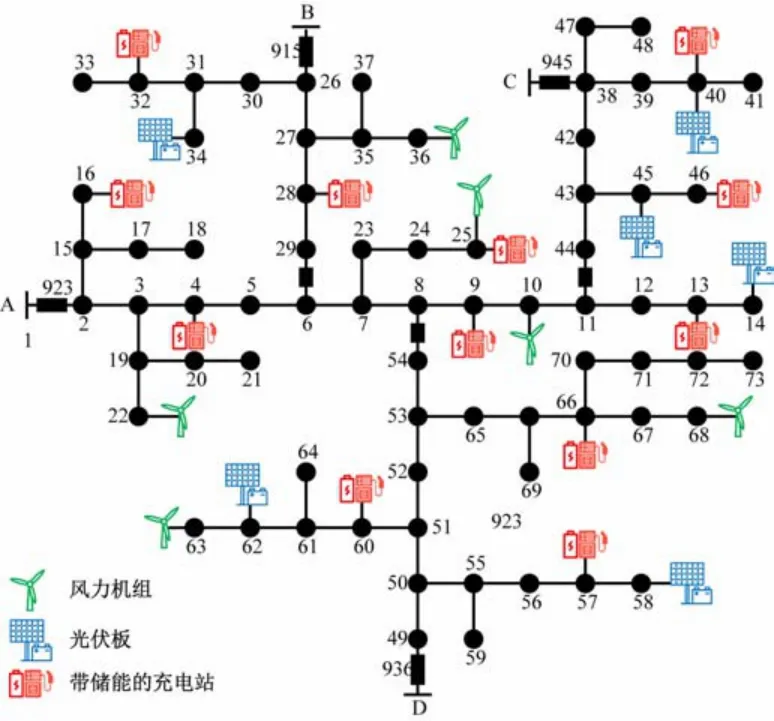
圖2 規劃區域電網拓撲

4.1 仿真結果分析

假設圖2 中4 個變電站出線均正常運行，聯絡開關也處于閉合狀態，充電站配置的儲能系統在負荷曲線低谷時間充電一次，在白天負荷高峰時段放電一次，在MATLAB中編寫程序，將所有參數信息帶入本文所提模型中進行求解，規劃區域內電動汽車充電站的最優規劃方案如表1 所示。

表1 充電站最優規劃方案

當變電站B 發生永久性故障時，饋電線路915 開關斷開隔離，饋線915 的負荷由變電站A、C和D提供支撐。將各類參數帶入所提模型，電動汽車充電站的最優規劃模型如表2 所示。

表2 故障下充電站最優規劃方案

上述兩個場景（未發生和發生故障）對應的投資收益和投資成本的具體組成如圖3 所示。

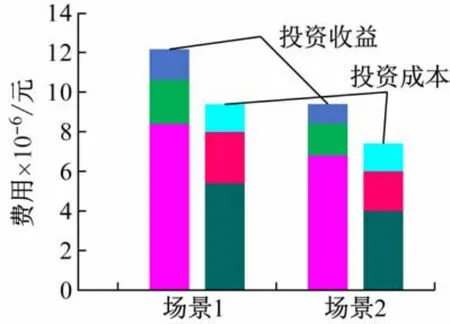
圖3 投資收益和投資成本的具體組成

表3 為考慮配電系統阻塞情況下使用戶滿意度最大的最優規劃方案。

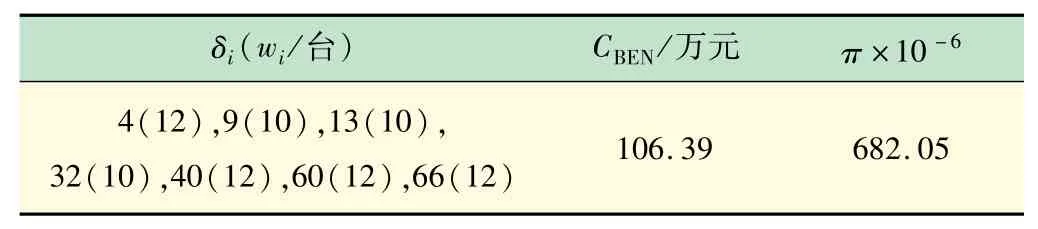
表3 故障下考慮阻塞時充電站最優規劃方案

當配電系統發生故障時，考慮電網阻塞和不考慮電網阻塞的節點邊際電價結果如圖4 所示。

根據表1～3、圖3 和4 可知，配電系統正常運行情況下，企業投資者不僅能獲得更大的投資收益，還能增強電動汽車用戶的充電體驗感和滿意度。但是，由圖4 可知，當配電系統出現故障且暫時無法恢復時，由于線路容量的約束，會出現線路阻塞，節點邊際電價就會發生變化，導致部分節點的充電電價被抬高，如節點13、節點25，即充電站向配電網購電的成本增加，則投資收益也隨之降低（由192.97 萬元降至106.39 萬元）。

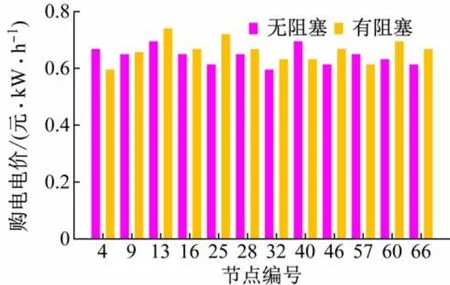
圖4 充電站備選點對應節點的節點邊際電價

然而，對于電動汽車制造企業而言，投資充電站的目的是吸引更多的消費者購買電動汽車，增加電動汽車銷量，充電站的投資收益可忽略。因此，在充電站年總投資成本差異較小的情況下，增強用戶體驗感更能使投資者增加市場占有率（滿意度由415.67 ×106增加至682.05 ×106）。

另外，由表2 和表3 可知，雖然電動汽車充電站的投資收益減少了44.86%，但是用戶的滿意度卻提升了64.08%，即規劃區域內電動汽車用戶在充電站內節約了大量時間，有利于吸引更多的電動出租車和電動網約車用戶來充電，也會刺激更多的消費者購買投資商的電動汽車或者充電設施。

綜上所述，隨著電力改革逐步深入，電動汽車充電站的運營公司可作為購電用戶參與市場化交易，電網阻塞對節點邊際電價的影響會越來越大，投資者需重點考慮該影響因素。

4.2 規劃方案參數特性分析

（1）儲能運行策略。電動汽車充電站所配置的儲能系統是在電網低谷時段對儲能充電，在負荷高峰時放電為電動汽車充電，不僅能響應電網公司的需求側管理，降低電網運行風險，而且能利用電價價差套利。但儲能系統投資成本較高，容量有限，充一次電不能滿足電動汽車充電站1 d 的放電運行，儲能系統不同充放電次數下充電站規劃方案如表4 所示。

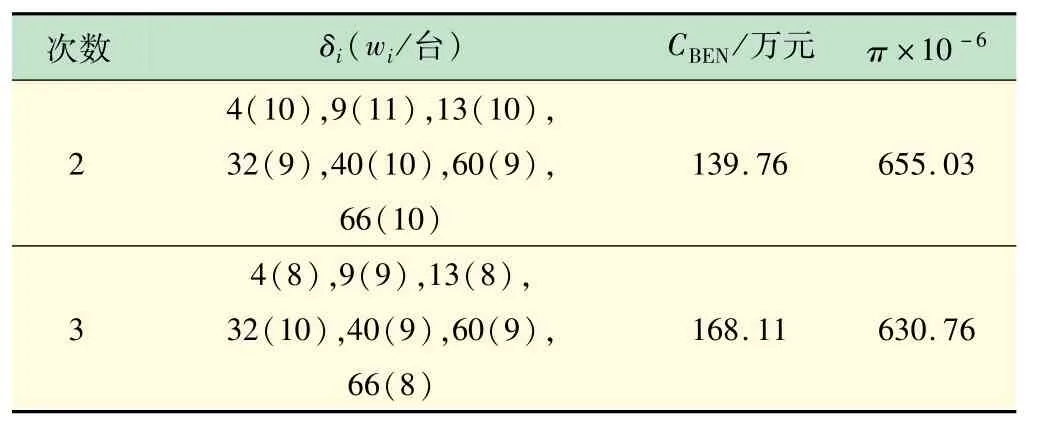
表4 儲能系統不同放電次數下充電站最優方案

從表4 可知，儲能系統在1 d 內的充放電次數不同會影響電動汽車充電站站內充電機數量，投資收益略微提升，因為投資成本減少了。充電用戶滿意度略微下降，由于充電機數量減少了，等待時間略微延長，但總體效果還是可以保證。

（2）電動汽車滲透率。電動汽車制造企業投資運營電動汽車充電站多為了吸引消費者購買電動汽車，則應考慮電動汽車保有量逐漸增加，充電負荷需求增加，假設電動汽車保有量在前文的基礎上再增加50%，在模型其他參數不變的情況下，對所提方法進行求解，充電站最優規劃方案如表5 所示。

表5 故障下不同滲透率時充電站最優方案

從表5 可以看出，為了滿足更多電動汽車充電用戶的需求，電動汽車充電站的充電機數量增加，使用戶等待時間降低，客戶體驗感和滿意度都得到了大幅度提升。雖然投資收益增長較小，但為吸引更多消費者和保證電動汽車用戶不流失，構建完善的充電服務網絡對投資企業很有優勢。不僅如此，完整的充電服務網絡還能吸引其他電動汽車品牌的用戶。

5 結論

在電力市場交易開放新環境下，傳統電網輸配電線路容量已經不能滿足電動汽車充電站運營公司作為獨立購電單元參與市場交易的要求，對即將投資電動汽車充電站的社會企業不利。本文考慮了電網阻塞對電動汽車充電站的影響，并重點關注充電用戶對充電服務的滿意程度，以保證投資者和充電用戶兩者利益的平衡。所得結論如下：

（1）基于節點邊際電價模型，搭建了含電動汽車充電站的配網節點邊際電價數學模型，可以較好反映充電站接入配網后的電網阻塞情況。

（2）將電動汽車制造企業作為電動汽車充電站投資者，建立了計及投資者和充電用戶雙方利益的電動汽車充電站雙層規劃模型，分別以投資收益和充電滿意度為各自目標函數。

（3）采用實際配電系統作為算例，采用改進遺傳算法對所提模型進行仿真分析，并討論了充電站配置儲能系統充放電次數和電動汽車滲透率對本文數學模型的影響，仿真結果表明了本文所提模型的合理性，并具有一定的工程指導意義。