基于VMD-PCA-SVM的電能質量擾動辨識

胡漢鋮，劉明萍，張 震，張鎮濤，汪慶年

（南昌大學信息工程學院，南昌 330031）

0 引言

近年來隨著光伏發電、風電等間歇式、分布式新能源的并網以及大量沖擊性、波動性、非線性負荷的投入，給電網造成一系列電能質量的問題，例如暫態振蕩、閃變和諧波污染等。為選取妥善合理的措施改善電能質量，必須對擾動信號進行正確、有效的辨識，這是開展電能質量檢測的前提和關鍵。

電能質量擾動辨識［1］主要包括特征提取與模式識別。特征提取是指提取擾動信號的特征量，通常采用信號分析法。常用的分析方法有短時傅立葉變換（short-time Fourier transform，STFT）［2］、小波變換［3］、S變換［4］及希爾伯特黃變換（Hilbert-Huang transform，HHT）［5-6］等。這些方法擁有良好的檢測效果，但也存在某些問題。STFT由于結構中缺少可變窗口，難以分析突變信號；小波變換的問題在于如何準確選取合適的基函數；S變換的難點在于如何確認窗函數的寬度；HHT 變換由經驗模態分解（Empirical mode decomposition，EMD）［7］與HHT 構成，其中EMD 存在較嚴重的端點效應、模態混疊問題。Dragomiretskiy等［8］獨創了變分模態分解（Variational mode decomposition，VMD），相較EMD 方法，它很好地克服了端點效應和模態混疊的缺陷，且計算效率更高、分解層數更少、魯棒性更好。因此，引進VMD算法對HHT變換進行改進，并應用于特征提取。

模式識別指的是將特征選擇所產生的特征向量進行識別分類。當今主流的方法有人工神經網絡［9］、支持向量機（Support vector machine，SVM）［10］和隨機森林［11］等。人工神經網絡具有數學靈活性，但也存在麻痹現象，學習速度不快；隨機森林因為采取了集成算法，其精度比大多數單一算法高，但當隨機森林中決策樹的數量過多時，訓練所需的時間和空間會較大；SVM是一種有監督的機器學習模型，具有優良的范化能力，但輸入參數過多，容易發生特征混疊，導致誤判。因此，引入主成分分析法（Principal component analysis，PCA），該方法能夠將特征向量進行降維投影，提取更加敏感的低維特征信息，將其與SVM 結合，能有效提升辨識精度，避免特征混疊等情況。

綜上所述，文中提出一種基于VMD-PCA-SVM 的電能質量擾動辨識方法。引入VMD 改進HHT 算法，用于分析擾動信號，得到邊際譜作為特征向量，將特征向量用PCA降維，用SVM 分類器進行分類識別。通過比較分析，仿真試驗表明該方法的可靠性和準確性。

1 算法原理

1.1 VMD分解

VMD是一種全新的以HHT、維納濾波為基礎的自適應分解法。原信號通過VMD 搜索約束變分模型的最優解，可被分解為若干組帶有稀疏特性的本征模態函數（Intrinsic mode function，IMF）分量。區別于EMD算法，IMF分量被設定為調幅-調頻信號［8］：

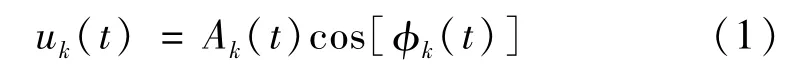
式中：φk為瞬時頻率的積分，即相位；Ak為瞬時幅值。假定各個IMF分量具有有限帶寬與中心頻率，且估計帶寬最小，那么可得約束模型：

式中：K為IMF 的個數；δ（t）為沖激響應；f為輸入信號；ωk為中心頻率。將懲罰因子α與拉格朗日算子λ相結合，把式（2）中的約束模型轉變為非約束模型：

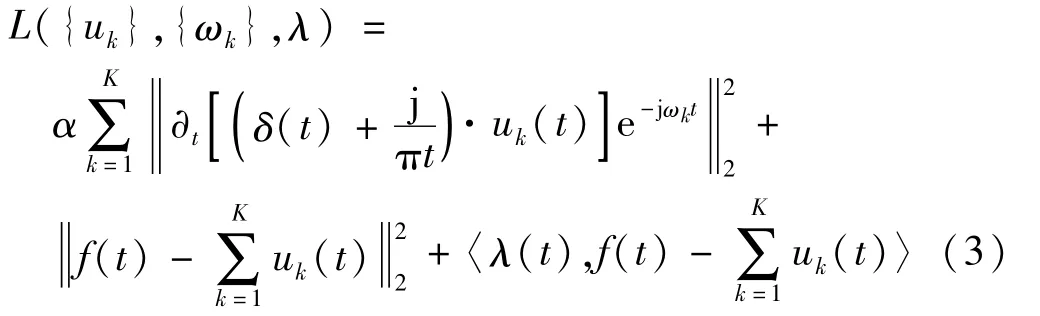
使用交替方向乘子求解式（2）中“鞍點”，可得uk和ωk。對uk，ωk，λ在頻域上更新：

式中，τ為更新因子。

VMD算法迭代求解的過程如下：

（1）初始化｛uk｝、｛ωk｝、λn和n；

（2）根據式（4）～（6）更新｛uk｝、｛ωk｝、λn；

（3）循環更新直至：

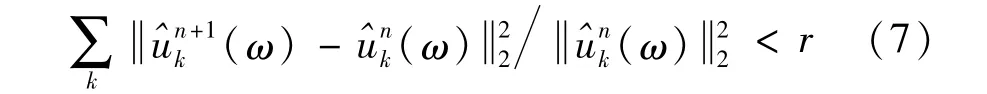
式中，r表示閾值。經過上述過程，VMD 分解得k個IMF分量。

VMD算法的核心在于構造變分問題，尋找變分最優解，明確每個IMF 分量的帶寬與中心頻率，使得分解得到的各IMF的帶寬之和最小，實現信號的有效分離。相比于EMD算法，它有更完整的數學理論作為支撐，從原理上克服了模態混疊與端點效應的問題［12］。

1.2 VMD-HHT邊際譜

借助HHT對VMD 分解所得的各個IMF 分量進行有效處理，原始信號可表示為：

式中，ωi、ɑi分別為信號的瞬時頻率和瞬時振幅。

由于x（t）是關于時間和瞬時頻率的函數，故可以表示為：

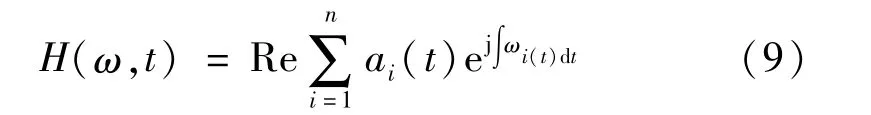
式中，H（ω，t）為HHT譜，對其積分，得到邊際譜：

邊際譜有效展示了電能質量擾動信號的幅值隨瞬時頻率的變化情況［13］。常用的功率譜只是能反映信號某一頻率存在的可能性，而邊際譜則可以說明某一頻率是否真實存在，表征某特定頻率在不同時刻所對應的幅值（或能量）之和。此外，邊際譜與常用的功率譜相比，分辨率和準確性顯著提高，能夠有效地抑制能量泄漏。鑒于邊際譜的上述優點，故將其作為特征向量。

1.3 PCA算法

PCA是一種使用較為廣泛的數據降維算法［14］。其目的是朝數據變動最多的方向投影，抑或是說朝重構誤差最小的方向投影。PCA降維分析的步驟如下：

步驟1假設Xm×n是一個m×n（m≥n）矩陣，計算矩陣Xm×n樣本協方差矩陣Sn×n。

步驟2計算Sn×n的特征向量對應特征值x1，x2，…，xn，特征值按照從大到小排列。

步驟3依據特征值大小計算Sn×n的第i列向量貢獻率θi以及前r維矩陣累計貢獻率Θr：

步驟4依據Θr的大小明確投影矩陣的維數r，其中Θr最少為70%，通常取85%～95%之間。

步驟5投影矩陣Sn×r由矩陣Sn×n取前r維得到，將需要降維的矩陣Xm×n與之相乘，獲得降維后的矩陣Tm×r：

PCA通過數據降維，找出變化大（即方差大）的特征向量，去除變化小（即方差小）的特征向量，得到最有效的數據特征向量。

1.4 SVM分類原理

SVM通過核函數的引進，將低維空間中的線性不可分樣本受非線性映射投影至高維空間中，變為線性可分樣本。在分類時，SVM 的中心思想在于建造一個超平面用作決策曲面，使負、正樣本的邊緣距離最大化［10］。其原理如下：

定義樣本集｛（xi，yi），i=1，2，…，N｝，xi為輸入向量，yi為類別標記，xi∈Rn，yi∈｛+1，-1｝。分類時，設存在分類界面：

式中：ω為權重向量；b為偏置向量。樣本點與分類界面距離為：

最優分界面應該滿足D最大，因此可轉化為二次優化問題：

引入拉格朗日函數求解：

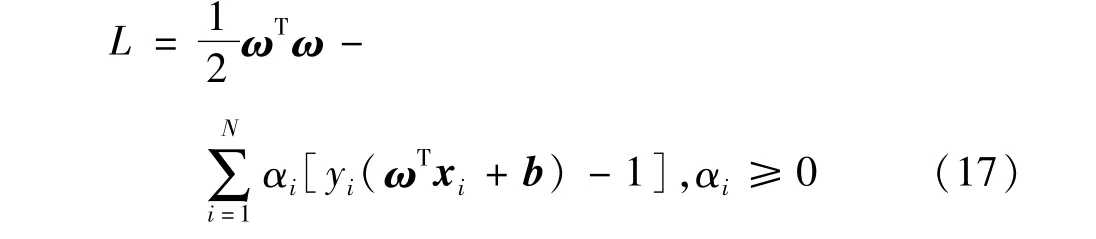
式中，αi為拉格朗日乘子。則得到對偶問題：

最后可得最優分類函數：

當處理非線性問題時，采用核函數K（xi，x）替代點積（xi·x），最優分類函數為：

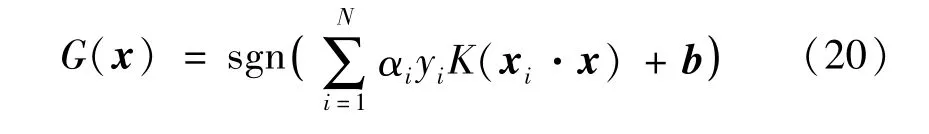
2 VMD-PCA-SVM 辨識模型

鑒于VMD 的優勢，故將其代替EMD，對HHT 變換進行改進。邊際譜能夠準確有效表征信號頻率的能量分布，故將其作為特征向量。選用PCA對邊際譜特征量開展降維處理，有效減少了邊際譜特征量的冗余信息并降低特征向量的維度，實現了二次特征處理。將PCA所生成的特征向量對SVM 分類器展開訓練，建立VMD-PCA-SVM辨識模型，如圖1 所示。

圖1 VMD-PCA-SVM辨識模型

該模型的主要步驟如下：

步驟1使用仿真軟件生成電能質量擾動信號，分成兩組用來進行訓練和測試。

步驟2將訓練信號進行改進HHT，PCA降維，然后對SVM分類器展開訓練。

步驟3將測試信號重復上述步驟，輸入訓練后的SVM分類器，最后得到辨識結果。

其中，SVM 分類器選取Matlab2017a 自帶的LibSVM分類器，選擇高斯徑向基核用作其核函數，即：

式中，σ 為掌管核函數高度的參數。LibSVM 可通過“交叉驗證”自動選擇最優核參數［14］。

3 仿真及實驗分析

3.1 仿真模型建立

針對這些復雜多變的電能質量擾動信號，國內外的研究多數在采用限定條件后，每種擾動生成隨機的數百樣本，形成完整數據庫，然后輸入分類器進行訓練和試驗。參考文獻［5，10］中建立包括標準信號在內的電能質量擾動信號的仿真模型，限定范圍見表1。仿真模型中：L為信號，基頻f取50 Hz，電壓幅值A均歸一化為1（p.u.），u（·）為階躍函數，ω為擾動信號的額定角頻率，T表示信號周期。

表1 電能質量擾動信號模型

3.2 邊際譜及PCA降維

使用Matlab2017a，根據表中的仿真模型，采樣頻率取5.7 kHz，信號長度為9 個周波，1 024 個采樣點，隨機生成9 組仿真信號，在信噪比（Signal to noise ratio，SNR）為40 dB條件下，用改進HHT 變換進行分析。采用VMD對信號展開分解，默認分解成4 階IMF分量。列舉閃變擾動信號的分解波形，如圖2 所示。對各階IMF分量采用HHT，得到各信號的邊際譜并歸一化，如圖3（a）～（i）所示。將生成的邊際譜特征向量進行PCA降維。設定滿足Θr≥95%時的r為PCA的投影維數取值，生成的PCA 降維效果圖如圖4 所示。由圖4 可見，當取維數r=1 的時候，Θr就超過70%；當在維數r=4 的時候，Θr已然達到95%，滿足要求，因此PCA選取4 維作為降維投影維數。

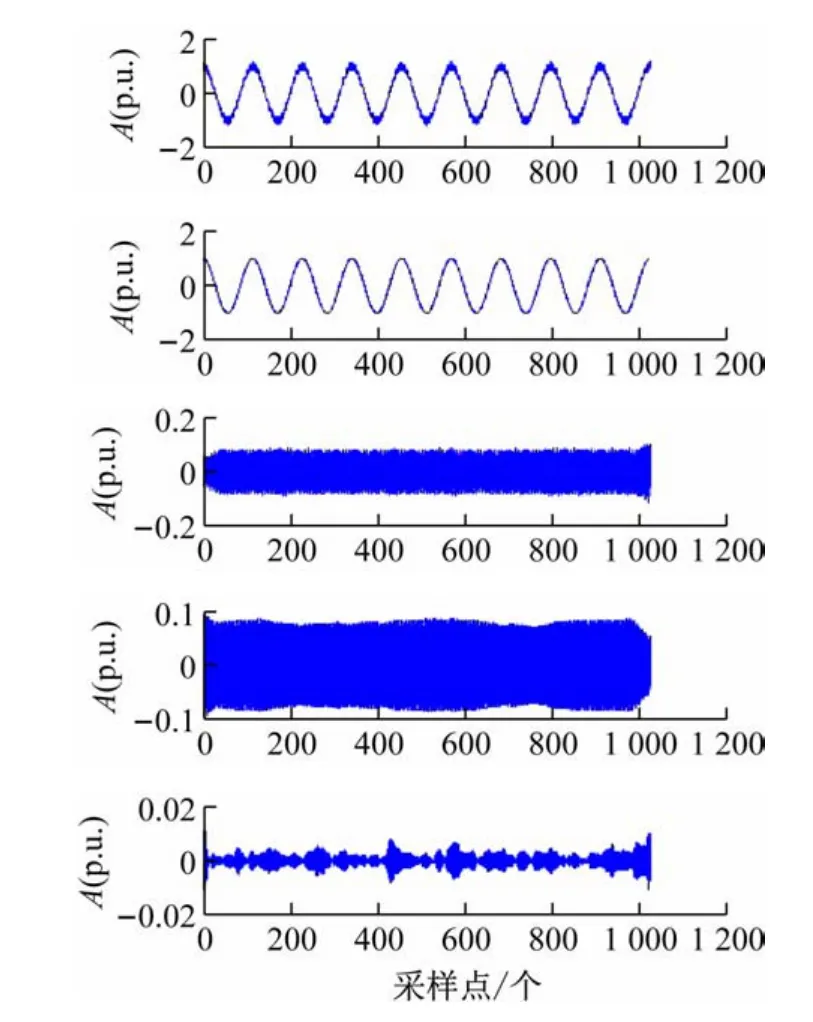
圖2 SNR=40 dB時閃變信號的VMD分解波形

圖3 SNR=40 dB時擾動信號的歸一化邊際譜

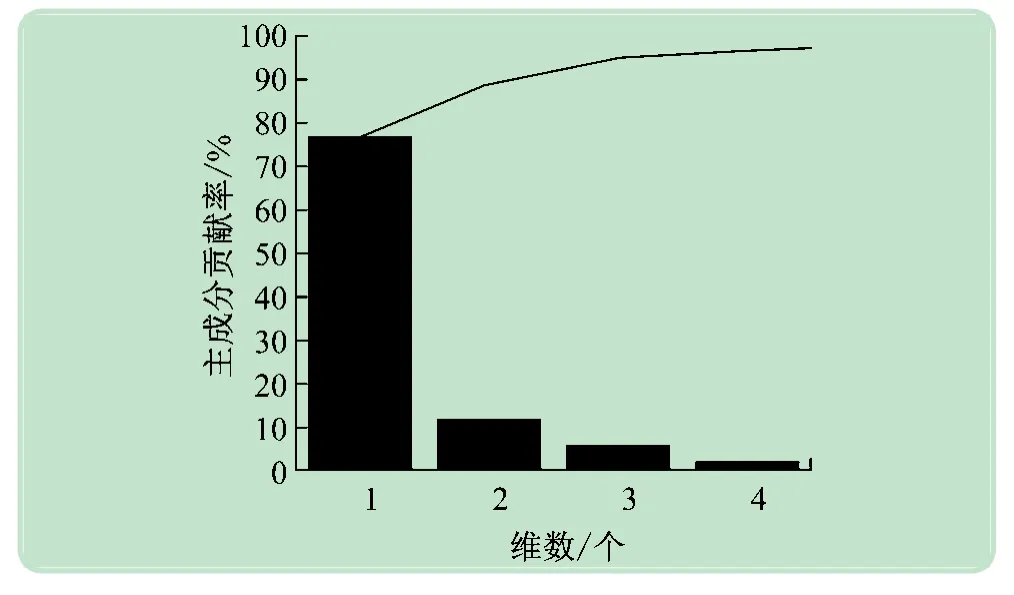
圖4 信噪比為40 dB時PCA降維效果圖

3.3 仿真測試及結果對比

根據表1 中的模型，使用Matlab2017a隨機產生包括標準信號和8 種電能質量擾動信號在內的9 組信號集，每組信號集生成1 000 個樣本，在疊加高斯白噪聲后，生成無噪聲和SNR分別為30、40、50 dB 的試驗信號。在同一高斯白噪聲下，取每組試驗信號800 個樣本，共7 200 個樣本進行訓練，剩下每組200 個樣本，共1 800 個樣本進行測試。最后將樣本輸入VMDPCA-SVM辨識模型中。辨識結果見表2。

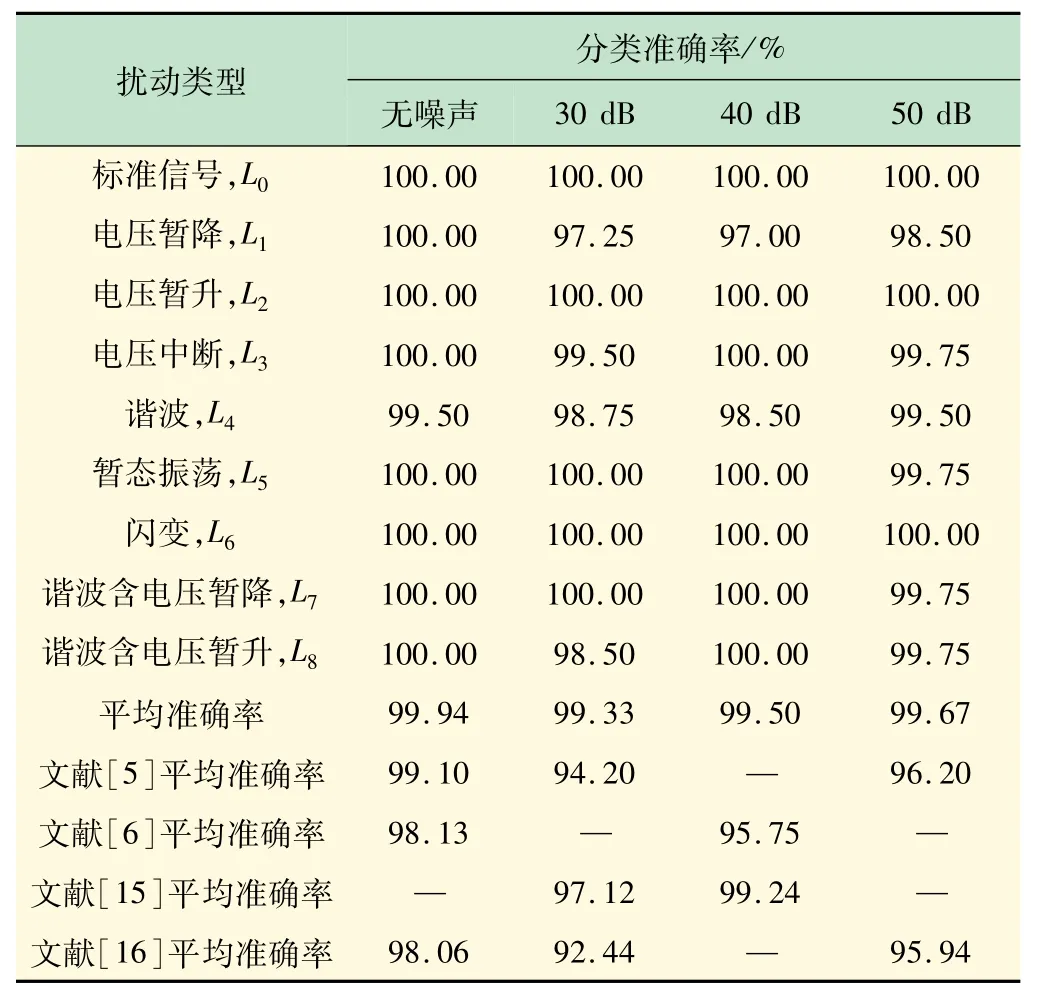
表2 辨識結果及對比

由表2 可知，在無噪聲的條件下平均分類準確率為99.94%，在SNR等于30、40 和50 dB的條件下，平均準確率分別達到99.33%、99.50%和99.67%，均超過99%，可見魯棒性和準確率良好。相比其他文獻所用的的方法，特別是文獻［5-6］中提出的類似改進HHT的方法，文中所用方法有更大的優勢，準確率和魯棒性皆有明顯提升。

4 結語

文中提出了一種基于VMD-PCA-SVM的電能質量擾動辨識方法，為電能質量擾動辨識提供了一種新思路。經過大量仿真試驗，文中結論如下。

（1）該方法不僅適合于單一電能質量擾動檢測，而且能精確識別2 種復合擾動，在無噪聲和3 種信噪比的條件下，平均準確率均高于99%，最高可達99.94%。

（2）VMD算法本身具有自適應好、分解效率高及魯棒性強的特點，它在數學原理上克服了模態混疊和端點效應，引入VMD算法來改進HHT算法，與其他類似文獻對比，其優勢通過優異的分類準確率和魯棒性得到充分體現。

（3）該方法也存在一些不足，例如VMD算法計算復雜度較高，實時性差，SVM 所需訓練樣本較多等，需要日后更多的改進。該方法測試是通過仿真平臺實現，是否能夠有效應用在實際工作中，還有待進一步探索。