圖形化編程在小學數學中的應用
——以列舉法為例

◎山東省臨沂第七實驗小學 池成英

山東省臨沂高都小學 范偉

Scratch是麻省理工學院開發的一款面向兒童的圖形化編程軟件，因其簡單易學、拼搭方式有趣而受到眾多師生歡迎。目前Scratch在教學方面的應用主要有兩類：一類是作為信息技術課堂上的編程工具，另一類是融入數學教學中。Scratch與數學融合有助于提高學生的數學邏輯思維能力，幫助他們迅速掌握數學知識。

本文通過雞兔同籠、牧童分杏、探索圓周率3個案例來講述Scratch在小學數學課堂教學中的應用。

一、Scratch與數學

數學是一門重要的課程，然而，數學中繁雜的計算、復雜的模型、抽象的邏輯往往使學生退卻，應用Scratch能有效幫助學生消除恐懼，激發他們學習數學的興趣。Scratch中的八大代碼模塊與數學知識有著千絲萬縷的聯系，例如：運動代碼模塊可解讀數學圖形的位置和運動的關系，運算代碼模塊將數據計算簡單化。

二、Scratch在數學中的具體應用

如何用Scratch解決數學實際問題？現采用嘗試列舉、一一列舉和無窮列舉這3個列舉法進行說明。

1.雞兔同籠

今有雉兔同籠，上有三十五頭，

下有九十四足，問雉兔各幾何？

學生看到這個題目后往往會用嘗試列舉的方法，盲目猜測雞和兔子的數量，經過多次無序的列舉，才找到正確答案。或者，他們推出雞兔的數量關系為“雞的腳數＋兔子腳數＝總腳數”，利用方程式算出答案。而Scratch軟件可以運用變量、隨機數、運算積木等高效解題。

首先將變量“雞的只數”和“兔子只數”設置為0，在0~5隨機選1個數字為雞的只數（如圖1），再利用運算積木進行等量關系式編寫（如圖2）。如果隨機數滿足“雞的腳數＋兔子腳數＝總腳數”這個等式，那么可得出雞的只數，兔子的只數便設為總頭數減去雞的只數（如圖3）。由于整個程序（如圖4）是重復執行的命令，所以加上重復執行積木。

圖1

圖2

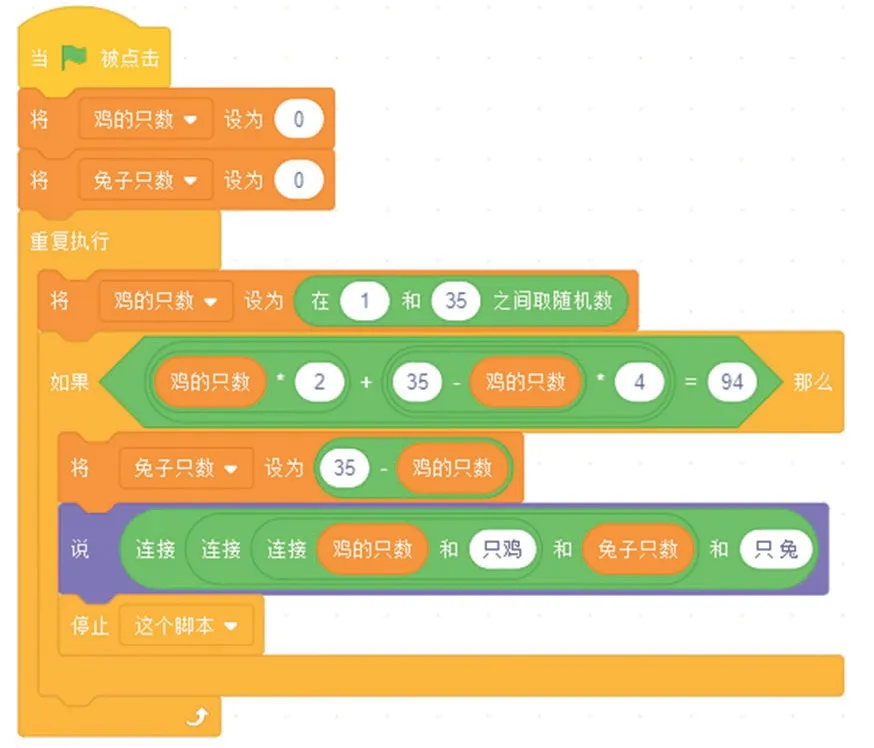
圖3

應用Scratch，學生可以迅速得出最終答案，既感受到了信息技術的優勢，又梳理出題目邏輯，掌握題型規律，提高了運算能力，從而舉一反三，快速解決類似數量關系的問題。

2.牧童分杏

牧童分杏各爭競，不知人數不知杏。

三人五個多十枚，四人八枚兩個剩。

讀完這首習題詩并理解后，要想知道有幾個牧童幾顆杏，我們可以一一列舉，從“1”開始驗證，最終找到答案。但是一一列舉耗時長，計算麻煩，借助Scratch可解決這一問題。

先設置變量“牧童”的人數為1，由于牧童的最終數量未知，我們先估算人數在50以內，如果人數多于50，加大數字即可。再利用“如果……那么……”積木，“如果”牧童人數不滿足等式：牧童牧童“那么”人數加“1”，一一列舉直到牧童人數滿足關系式：牧童牧童（如圖5），最終求出牧童的人數。杏的數量則為圖6所示，整個編程設計如圖7。

圖5

圖6

圖7

牧童分杏問題涉及的數據較小，可以用一一列舉的方法得出答案。當數據較大時，Scratch通過分析部分數據找到共同特征，最后概括出一般規律，讓學生理解由個別到整體的推理過程，培養學生的歸納能力。

3.探究圓周率

π=3.141 592…… ？

為了進一步探究圓周率π，我們可以運用“割圓術”進行計算。割圓術，就是通過不斷增加圓內接正多邊形的邊數來求出圓周率。把圓等分成若干份，依次連接形成正多邊形，分的份數越多，正多邊形的周長就越接近圓的周長。再借助圓的周長公式，便可得到圓周率：

無窮列舉法的計算過程非常復雜，我們通過常規的計算無法得到準確數值。運用Scratch先添加兩個變量“邊的數量”和“圓周率”（如圖8），將邊的數量設置為0，利用重復運行來增加邊的數量，每運行一次，邊的數量加“1”，當運行邊的數量為1000時，圓周率的數值是3.141 587 467 8（如圖9所示），當邊的數量趨于無窮大時，得出π為無限不循環小數。

圖8

圖9

借助Scratch無窮列舉邊的數量，得到最接近的答案，學生可感受圓周率π數值運算的嚴謹性，在解題中進行幾何空間想象，也鍛煉了邏輯思維能力。

三、應用Scratch的收獲

Scratch在數學中的應用豐富了學生的數學解題方法，讓數學思維可視化，也給老師提供了一種新的教學模式。學生在運用Scratch的過程中，提升了運算能力、概括能力和邏輯思維能力，逐漸形成良好的數學素養和綜合思維。希望Scratch能在更多的學科中開花結果。