基于FLAC3D的拉林鐵路沿線風積沙液化特性研究

崔 雍，薛春曉，李 舟，孔令偉

(中鐵西北科學研究院有限公司， 蘭州 730030)

川藏鐵路起于四川省成都市，經雅安、康定，昌都、林芝和山南，終于西藏自治區拉薩市，線路總長約1 629 km。拉林鐵路是川藏鐵路的重要組成部分，線路起于拉薩火車站，沿拉薩河而下，經貢嘎轉向東，經山南、朗縣、米林，跨越雅魯藏布江到林芝站[1-2]。拉林鐵路2012年3月列入國家《十二五綜合交通運輸體系規劃》的快速鐵路專欄，設計速度160 km/h，是國鐵Ⅰ級單線電氣化快速鐵路。全長約433 km，與拉日鐵路共線近33 km，新建里程近400 km。

新建拉林鐵路位于青藏高原東南部，屬于岡底斯山與念青唐古拉山、喜馬拉雅山之間的藏南谷地，雅魯藏布江中游，海拔在2 800～3 700 m。山高谷深，氣候極端惡劣。面臨的主要工程地質問題有：崩塌、滑坡、錯落、泥石流、溜沙坡(又稱碎屑流或巖屑坡)、水毀、冰害、風沙、高烈度地震與活動斷裂、熱害、高地應力(巖爆與大變形)等[3-7]。

拉林鐵路沿線穿越多個地震帶，地震活動強烈、大地震頻發。此外，拉林鐵路沿線風沙地段廣泛分布，約占線路全長的10%以上，線路所經地區地形復雜、高差大、風向多變、山谷風作用強烈，路基工程所面臨的高烈度區風積沙液化問題特殊而復雜。國內外學者雖然進行了一些研究，但由于拉林鐵路部分區域地表被風積沙覆蓋，且地下水位高、液化層顆粒比較細(如扎囊車站)，沙土性質完全不同于普通沙土，目前的研究成果只能起到一定的參考作用[8-15]。例如，陳文化等[16]對沙土液化產生的原因、影響因素和主要判別方法作了簡要的回顧，并對近年來的研究現狀進行了評述和對未來發展趨勢提出了一些看法；牛琪瑛等[17]利用FLAC軟件對水泥土樁加固的液化沙土地基建立模型并進行地震響應分析；呂西林等[18]應用FLAC軟件對液化場地自由場體系的地震響應進行三維完全非線性分析，并與振動臺試驗結果進行了對比；郭英[19]基于有限差分軟件，建立了能合理反映不同密實度未加固和水泥土樁加固液化土模型地基，分析比較了同一密實度條件下加固與未加固地基孔隙水壓力、孔壓比、豎向位移、表面加速度等的變化；王余慶等[20]利用等價非線性有效應力動力分析二維有限元程序，對飽和沙層的液化特點及礫石排水樁與地面壓重的抗液化效果進行了分析。綜上所述，基于FLAC3D技術開展川藏鐵路高烈度區風積沙液化特性的研究具有重要的意義。

1 模型簡介

1.1 模型尺寸和計算參數

沙土自由場的動力分析模型計算域尺寸為20 m×20 m×25 m，結合現場實際情況，將土層劃分為3層，上層為粉土，中、下層為沙土，上、下層為非液化層，中層為可液化層，地下水位位于液化層表面，土層的計算參數見表1。

表1 模型土層計算參數

1.2 網格劃分與邊界條件

由于本次計算模型為規則的長方體，因此，數值模擬中采用了六面體網格(圖1)。FLAC3D軟件中提供了靜止(黏性)邊界和自由場邊界兩種邊界條件來減少模型邊界上波的反射。數值模擬中采用自由場邊界，即主體網格的側邊界通過阻尼器與自由場網格進行耦合，自由場網格的不平衡力施加到主體網格的邊界上。由于自由場邊界提供了與無限場地相同的效果，因此，向上的面波在邊界上不會產生扭曲。

圖1 施加自由場邊界條件的網格

1.3 孔壓模型

在FLAC3D軟件中主要有Finn模式和Byrne模式兩種塑性體積應變增量公式，本次數值模擬采用建立在摩爾-庫倫模型基礎上的Finn模式，它反映了孔壓在地震動作用下的累積效應，此外，該模式假定動孔壓的上升與塑性體積應變增量相關。基本原理為：當沙的密度和往返作用次數一定時，體應變與豎向靜正應力無關，只取決于往返剪應變幅值；當往返剪應變幅值一定時，體應變隨往返作用次數的增加而增加。每一次往返作用引起的體應變增量取決于已經產生的永久應變數值和即將作用在土體上的剪應變幅值。假設即將作用的剪應變為第N次，那么第N次產生的永久體應變增量與之前已經產生的永久體應變關系可用下式表示

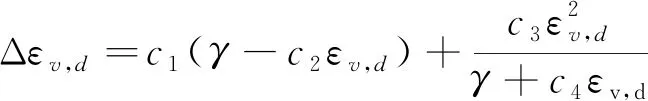
(1)

式中，Δεv，d為第N次產生的永久體應變增量；γ為第N次作用的剪應變幅值；εv，d為第N次往返作用以前已經產生的永久體應變；c1=0.8，c2=0.79，c3=0.45，c4=0.73。

1.4 模擬工況

為較為深入地了解研究區飽和沙土的動力特性，以及各種因子對動力特性的影響，沙土自由場模擬總計14種工況，各工況的計算參數見表2。研究區段位于8度烈度區，地震動峰值加速度為0.30g。

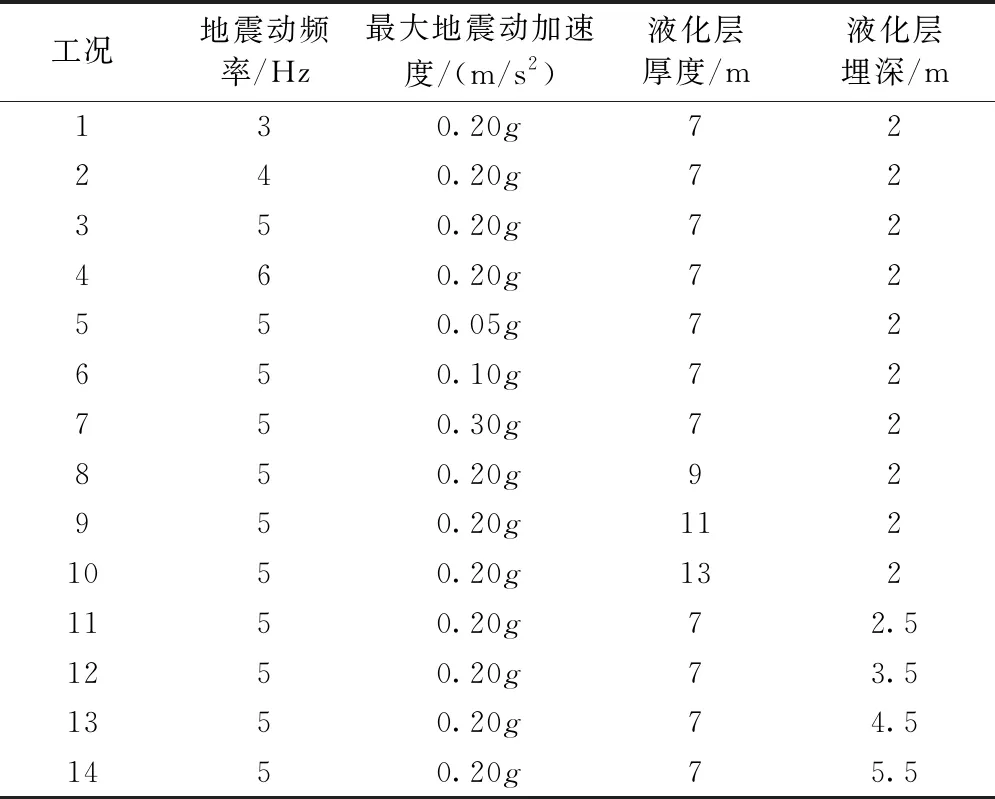
表2 自由場模擬各工況參數

2 風積沙液化特性及影響因素

2.1 自由場液化特性分析

孔壓比是在循環應力作用下沙土的孔隙水壓力增量與側向有效固結應力的比值，可在一定程度上反映沙土的液化趨勢，自由場中孔壓比越接近于1.0，說明該區域沙土越容易液化。圖2為工況3條件下自由場的超孔壓比分布云圖，從圖2不難看出，可液化層大部分區域的孔壓比在0.9以上，表明在地震動環境作用下研究區可液化沙土的大部分區域存在液化的可能，需根據預測的地震烈度進行處理才能保障該地基上建筑物的安全。此外，值得注意的是毗鄰非液化層的可液化沙土(簡稱毗鄰層，下文相同)孔壓比明顯偏小，說明非液化土層對相鄰的可液化土層液化具有一定的抑制作用。

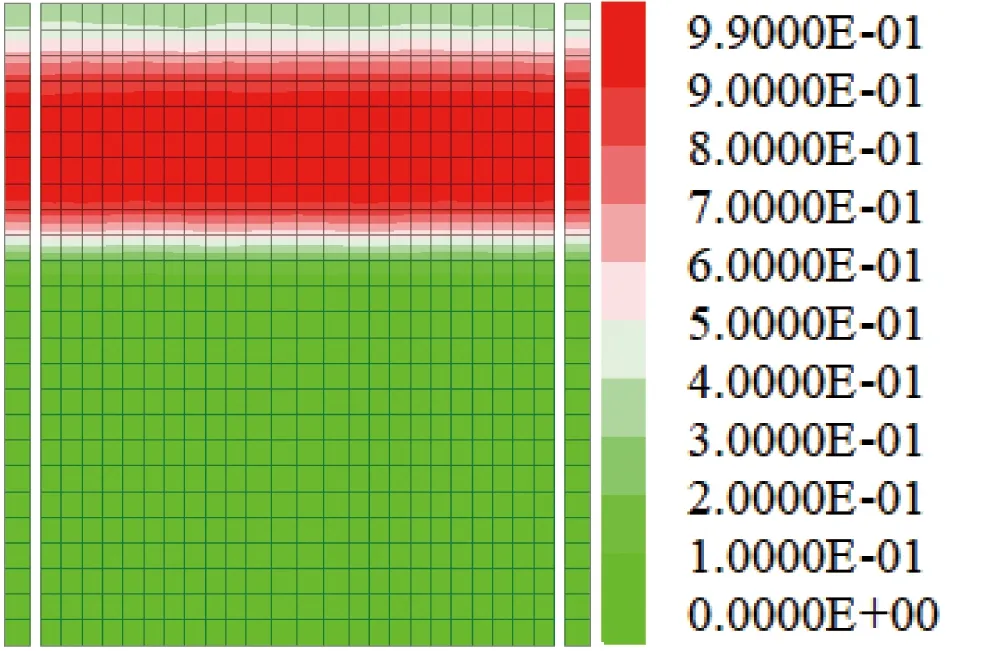
圖2 自由場的超孔壓比云圖

為更直觀地分析可液化層中飽和沙土的液化趨勢，提取工況3土層中的超孔壓比時程曲線(圖3)，可以看出，可液化沙土中各深度處孔壓比變化趨勢基本一致，大致可分為兩個階段：急劇上升階段和振蕩平穩階段，曲線拐點大致在1～2 s。但受鄰近非液化土層及埋深的影響，曲線在細節上存在差異。除毗鄰層以外，其余各層的孔壓比均達到了1.0，但各土層孔壓比峰值到達時間明顯不同，深度越大孔壓比達到峰值所需時間越長，說明飽和沙土的液化并非同時到達，而是上部土層首先液化，之后才是中、下部土層。

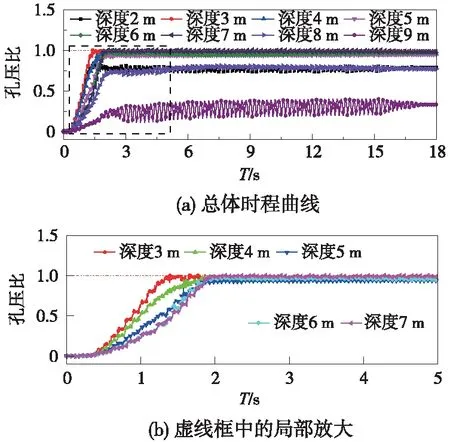
圖3 可液化沙土超孔壓比時程曲線

相關研究表明，松散的沙土在振動作用下，沙顆粒將會重新排列，導致土體密實度增加，從而會產生一定的沉降。因此，探索可液化沙土在振動環境下的沉降規律，可為液化地基上建筑物的沉降控制提供指導。圖4為工況3條件下不同埋深監測點土體的沉降時程曲線，不難發現，在動力作用前期，振密后的土體沉降迅速增大，待土體達到一定密實度后，土層沉降速率逐漸減小，沉降曲線隨時間趨于平緩。此外，注意到不同土層的沉降存在差異，埋深越淺，沉降量越大。

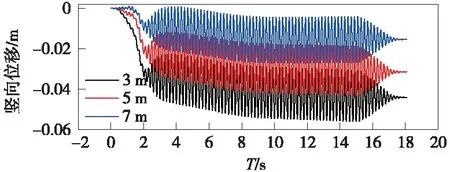
圖4 可液化沙土豎向位移時程曲線

2.2 加速度對自由場液化特性的影響

地震動加速度不僅能反映地震的烈度，也可以在一定程度上預估地震損失。了解不同加速度條件下的地震動，可以為地基抗震方案提供依據。圖5為不同加速度條件下自由場的超孔壓比云圖，從圖5可以發現，隨著地震動加速度的增大，孔壓比在0.9～1.0的區域(簡稱高孔壓比區域，下同)在逐漸擴大。上述現象說明，同等條件下，加速度越大地震動的能量越高，可液化沙土的液化范圍越大，對地基上的建筑物影響也越大。此外，值得注意的是毗鄰層的范圍隨著加速度增加呈遞減趨勢，說明隨著加速的增大非液化層抑制沙土液化的作用在逐漸減弱。

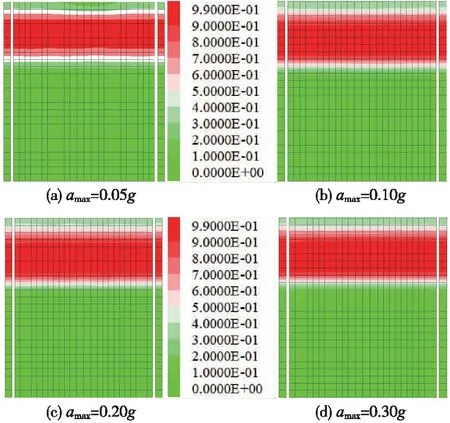
圖5 不同加速度條件下自由場的超孔壓比云圖

圖6為不同加速度條件下可液化沙土孔壓比時程曲線，可以看出，孔壓比隨時間的變化趨勢基本一致，即均存在急劇上升階段和振蕩平穩階段，但拐點的位置明顯不同。隨著加速度增加，曲線上拐點的位置逐漸向右移動，即達到孔壓比峰值的時間越長。說明加速度越大，同等條件下研究區沙土液化所需的時間越短。此外，還可以看出，加速度amax=0.05g時，僅深度3 m處的孔壓比峰值達到了1.0，而加速度amax=0.10g，0.20g，0.30g時，深度3～7 m時均達到了1.0。表明加速度較小時，雖然沙土可能達到液化狀態，但液化的區域較小。

注：圖6(a)～圖6(d)中的下圖為虛線框中局部放大圖

地震作用下，越靠近地表，豎向位移越大，故提取地表的豎向位移進行分析。圖7為不同加速度條件下地表豎向位移時程曲線，不難發現，隨著地震動加速度的增大，地表最終豎向位移呈遞增趨勢。主要原因在于：外界加速度越大，地震動蘊涵的能量越高，在同等條件下沙土振的越密實，從而使得同一位置的豎向位移越大。

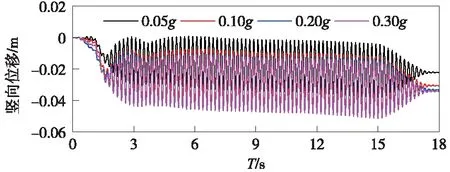
圖7 不同加速度條件下地表豎向位移時程曲線

2.3 頻率對自由場液化特性的影響

地震動頻率是影響沙土液化的關鍵指標，研究它對液化特性的影響對地基抗液化具有指導作用。圖8為不同頻率條件下自由場的超孔壓比云圖，可以看出，高孔壓比區域范圍隨著頻率的增大而逐漸擴大，說明頻率在3～6 Hz內，地震頻率越高，沙土可能液化的范圍在逐漸增大。

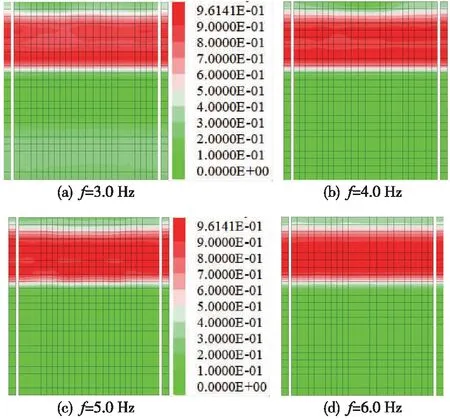
圖8 不同頻率條件下自由場的超孔壓比云圖

圖9為不同頻率條件下可液化沙土自由場的超孔壓比時程曲線，不難看出，各種頻率下孔壓比的變化趨勢基本一致，但曲線的拐點存在差異，頻率越小曲線的拐點越靠左，說明頻率越小達到孔壓比峰值所需的時間越短，即在3～6 Hz內，頻率越大地震液化所需時間越長。此外，注意到地震頻率越大，各層土體達到液化時的時間差越大，即下層土體液化的滯后性越強。

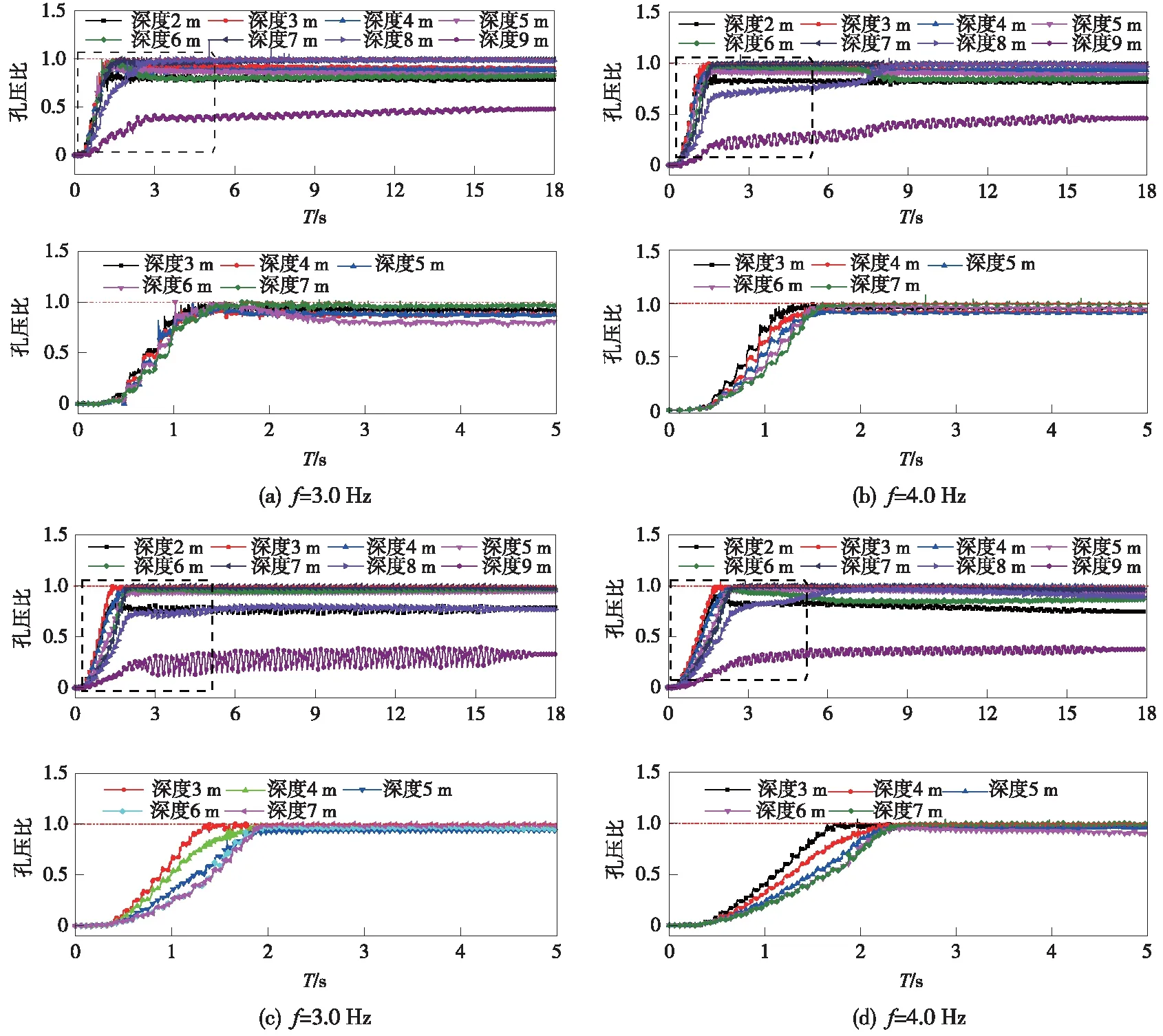
注：圖9(a)～9(d)中的下圖為虛線框中局部放大圖

圖10為不同頻率條件下可液化沙土自由場地表豎向位移時程曲線，分析變化趨勢不難看出，位移隨著時間的推移呈波動遞增趨勢，但各頻率條件下最終的豎向位移量存在差異。在頻率3～6 Hz內，隨著地震頻率的增大，可液化沙土的最終豎向位移呈遞增趨勢。在頻率6 Hz時，最終豎向位移約5 cm，而頻率3 Hz時，最終豎向位移約1.8 cm，前者豎向位移約為后者的3倍。

圖10 不同頻率條件下可液化沙土自由場地表豎向位移時程曲線

2.4 液化層厚度對自由場液化特性的影響

圖11為不同液化層厚度條件下自由場的超孔壓比云圖，厚度H對可液化沙土液化的影響顯著。隨著液化層厚度增加，高孔壓比區域由連續片狀分布逐漸分離為兩部分，且厚度越大兩部分之間的距離越大。此外，注意到中間層的超孔壓比在0.8～0.9，略小于上下兩層。

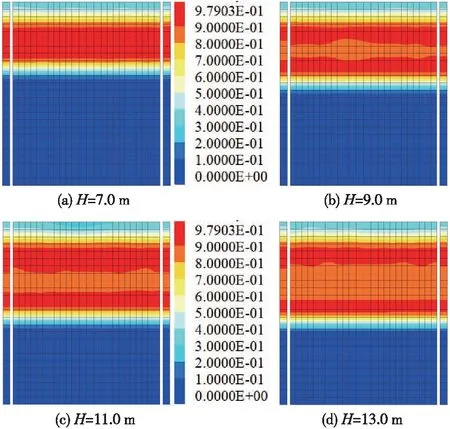
圖11 不同液化層厚度條件下自由場的超孔壓比云圖

圖12為不同液化層厚度條件下地表豎向位移時程曲線，趨勢顯示豎向位移隨著時間的推移呈波動遞增趨勢，并最終趨于穩定。此外，隨著液化層厚度增大，表層的最終豎向位移呈遞增趨勢。厚度為13 m時，最終豎向位移約為8 cm，而厚度為7 m時，最終豎向位移約為4 cm，前者豎向位移約為后者的2倍。

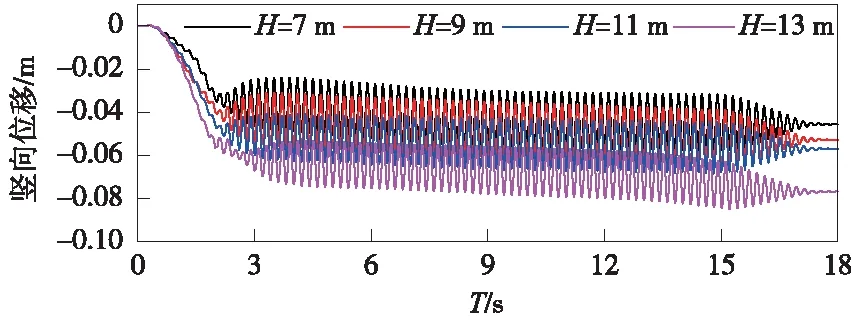
圖12 不同液化層厚度條件下地表的豎向位移時程曲線

2.5 液化層埋深對自由場液化特性的影響

圖13為不同埋深條件下自由場的超孔壓比云圖，可以看出，埋深對可液化沙土的液化趨勢影響非常顯著。當埋深由2.5 m增加至3.5 m時，高孔壓比區域由連續片狀分布逐漸分離為兩部分；當埋深由3.5 m增加至4.5 m時，上層高孔壓比分布區域呈遞減趨勢；當埋深增加至5.5 m時，上層高孔壓比區域幾乎消失。上述現象揭示了上覆土層厚度對可液化沙土的液化具有抑制作用，土層厚度越大抑制作用越顯著，這說明，可通過增加上覆土層的壓力來減小可液化層的液化趨勢。

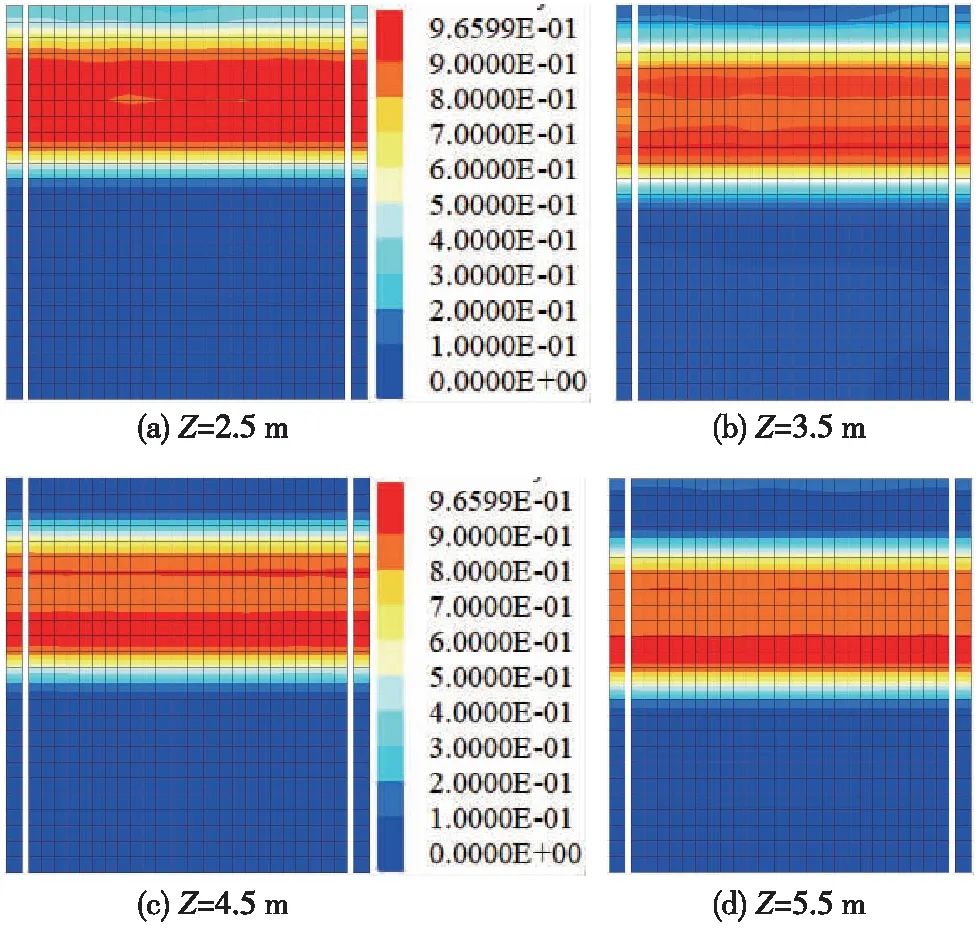
圖13 不同埋深條件下自由場的超孔壓比云圖

圖14為不同埋深條件下地表豎向位移時程曲線圖，不難看出，豎向位移在初期急劇增大，接著波動變化，最后逐漸穩定。對比不同埋深條件下的豎向位移時程曲線，可以發現，隨著液化層埋深的增大，表層的最終豎向位移呈遞減趨勢，再次驗證了上覆土體對液化的抑制作用。

圖14 不同埋深條件下自由場地表豎向位移時程曲線

3 結論

本研究基于FLAC3D軟件中的Finn孔壓模型，結合川藏鐵路拉林段風積沙液化路段的實際巖土參數，對不同工況下土層的地震響應特征進行了數值模擬，主要結論如下。

(1)在地震動作用下，可液化沙土中的毗鄰層孔壓比明顯小于其他區域，說明非液化土層對相鄰可液化沙土的液化具有一定抑制作用，且隨著加速度增大這種抑制作用逐漸減弱。

(2)在動力環境作用下，可液化沙土并非同時液化，而是具有時間差，即除了毗鄰層以外，上部土層首先液化，之后才是中、下部土層。

(3)地震動加速度與頻率對研究區飽和沙土的液化特性影響顯著，加速度越大或頻率越小，同一土層達到液化所需的時間越短。此外，隨著加速度或頻率的增大，沙土的液化區域和最終沉降量均呈遞增趨勢。

(4)可液化層厚度較薄時，高孔比區域呈連續片狀分布，隨著液化層厚度逐漸增大，高孔壓比區域逐漸分離為上、下兩部分，且兩部分之間的距離也在增大。此外，最終豎向沉降量隨液化層厚度增大呈遞增趨勢。

(5)上覆非液化土層越薄，飽和沙土的液化范圍越小，地表的最終沉降也越小，這表明可通過增大上覆非液化土層的重力來抑制液化層的液化程度。

(6)川藏鐵路沿線風積沙區的飽和沙土容易液化，在其上修筑建筑物時宜采取加固措施進行處理，以達到減輕或消除飽和沙土液化性，保障建筑物安全的目的。