雙無人機協同搬運的力位混合控制方法

周東升，楊忠，廖祿偉，徐浩，許昌亮，張秋雁

1.南京航空航天大學 自動化學院,江蘇 南京 210016 2.貴州電網有限責任公司,貴州 貴陽 550002

隨著無人機應用的不斷深化，無人機正逐漸成為一種空中作業平臺，除航拍外還用于完成諸如負載運輸[1]、空中抓取作業等任務[2-3]。無人機攜帶負載主要有夾持和吊掛[4-6]這2 種方式。負載運輸的應用場景包括快遞運送、救援物資投放等。應用場景的復雜性、負載類型的多樣性，給無人機的總體設計、機械結構和控制策略帶來新的挑戰。

對于大重量負載，無人機需要提供更大的升力；對于大尺寸負載，則需要改進無人機的構型以便運輸。因此，運輸大質量大尺寸負載，無人機的尺寸與質量也會隨之增大，并需配備大容量電池[7]。無人機質量和尺寸的增加不僅會影響其靈活性[8]，而且會產生更高的制造和維護成本。

針對單架無人機運輸大質量大尺寸負載的局限性[9-10]，有人考慮使用多架無人機配備高精度傳感器進行協同搬運，從而在不改變無人機尺度的前提下，有效提高其負載能力[11]。然而，多無人機在定位、控制和協作等方面存在較多問題，通信帶寬的限制是一項重要挑戰[12]。一般來講，多無人機之間的通信方式包括顯式通信和隱式通信2 類。顯式通信一般用于將控制信號或傳感器數據等信息直接傳遞給其他機器人[13]，隱式通信是指無人機與環境或其他無人機進行物理交互(如相互之間的交互力)或非物理交互(如視覺觀察)的作用，這種方式所需的信息由附著在無人機上的傳感器獲取。研究最多和最常用的方式是顯式通信方式，該方式易于分析，協作效率高，但在通信環境較差的情況下，可能會出現嚴重的問題。

協作搬運負載是多無人機協同作業應用的一個重要方向，應用發展前景良好，國外開展了大量研究。文獻[14]分析了使用一組無人機通過電纜來運輸大的有效載荷的問題，該結構的選擇是為了在電纜張力影響的情況下保證有效載荷的靜態平衡。文獻[15]針對2 架無人機對大型物體的運輸，研究了基于被動力控制的無人機協同控制問題。然而，這些研究方法多采用軟繩或電纜進行運輸，負載的擺動容易引起無人機的不穩定甚至失控。

為了解決上述多無人機系統通信以及負載擺動帶來的問題，本文設計了一種基于硬連接的隱式通信方式的力位混合控制方法。每架無人機與負載通過球形關節硬連接[16]，該球形關節具有3 個運動自由度并進行限位[17]，使得無人機的姿態動力學和負載的姿態動力學解耦，進而可以通過調整飛行器的姿態以及旋翼產生的推力大小來控制負載的運動。硬連接導致無人機與負載之間存在力的約束，為此采用導納控制技術[18]進行力的控制，其思想是通過感知外部的力來生成運動軌跡，調節無人機的運動，實現任意的力交互行為。本文設計的方法如下：1）給定主機期望的運動軌跡，主機和從機與負載硬連接，主機運動對負載產生力的作用，同時負載也對從機產生力的作用，從機通過力估計方法感知負載施加的作用力；2）通過導納控制技術改變從機的運動軌跡以適應受到的負載的作用力；3）對導納控制器輸出的運動軌跡設計一個外部的控制回路，并通過線性二次型調節器[19]實現主從機位置姿態的穩定控制，由于存在外部擾動力的作用，所以從機受到較小的力作用時導納控制器不啟動，僅通過位姿控制器實現位姿穩定控制，只有受到較大的力作用時，導納控制器啟動，從機根據受到的力作用進行運動。

1 數學模型

1.1 運動學建模

雙無人機與負載之間的硬連接方式如圖1 所示，為雙無人機協同搬運系統。定義坐標系I：為地球固連坐標系 ；B：為與機身固連的機體坐標系，i表示第i架無人機，原點與飛機質心重合；P：為與負載重心固連的坐標系。地球固連坐標系、機體坐標系和負載坐標系都滿足右手定則。

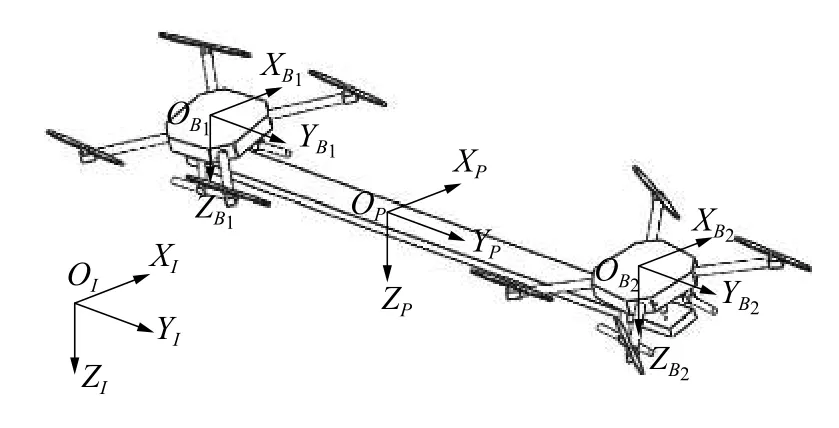
圖1 雙無人機協同搬運坐標系定義

圖2 為球形連接關節，外部球殼可以繞內部球頭轉動。做出如下假設：1）每個飛行器的機體坐標系Bi到負載參考坐標系P的相對位置是已知的，用向量表示；2）表示飛行器機體系Bi到負載坐標系P的旋轉矩陣。從而可以得到系統的運動學方程[20]為

圖2 球形關節

1.2 動力學建模

本文的雙無人機搬運系統的動力學模型通過牛頓-歐拉方程得到。為了方便后續控制方案的設計與研究，本文中系統的平動方程在地球固連坐標系下描述，轉動方程在負載坐標系下描述：

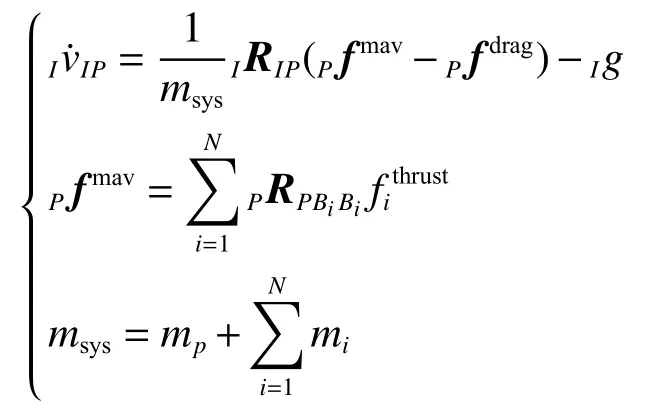
式中：Pω和分別為負載的加速度和角加速度；Pτmav為所有飛行器對負載施加的總力矩；Pτdrag為與空氣動力學相關的干擾力矩；為第i架無人機到負載的相對位置向量；PIsys為整個系統總的慣性，與負載慣性以及飛行器的質量和位置有關。

2 控制策略

由于主機和從機與負載之間都通過球形關節進行連接且相互之間不存在顯示通信，考慮采用基于導納控制[21-23]的控制策略，即2 架飛行器攜帶負載懸停在同一高度，向主機發送目標軌跡指令，從機通過感知負載傳遞的力進行跟隨運動，從機的控制策略如圖3 所示。

圖3 從機控制策略

2.1 力估計

主機接收指令并帶動負載一起運動，會導致負載對從機產生作用力，這個力采用卡爾曼濾波器算法[24-26]來估計，并確保濾波器是閉環穩定的[18]。選取狀態量ξK=(ξ,F)，給定系統為

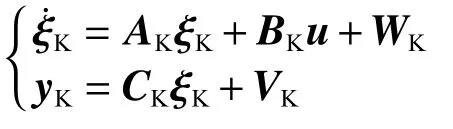
式中：ξK=(ξ,F)為選取的狀態變量，ξ˙K為其導數，ξ為從機三維位置、速度、歐拉角、角速度和角加速度信息，F為估計的力大小，u為輸入的力和力矩，AK、BK和CK為常數矩陣，WK和VK分別為過程噪聲和測量噪聲協方差矩陣。估計的狀態量為

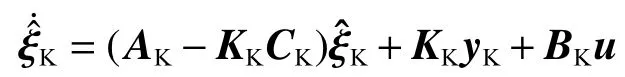
建立飛行器模型，平動動力學表示為

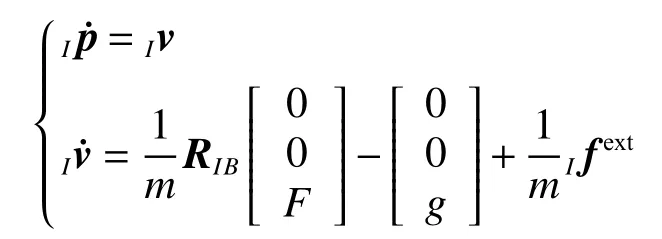
式中：I p和Iv為從機的三維位置和速度向量，和分別是它們的導數，m為從機的質量，RIB為從機機體系到地球固連坐標系的旋轉矩陣，F為從機旋翼產生的總推力，fext是施加在無人機上的外力。

轉動動力學可以近似表示為

在上述模型基礎上，卡爾曼濾波的狀態變量選擇為

由于外力和外力矩的動力學是未知的，所以假設它們僅由零均值白噪聲驅動。測量向量考慮了白噪聲的影響，定義為

濾波器的輸入向量由姿態和總推力給出[27]：

式中?cmd、θcmd和ψcmd分別為輸入的滾轉角、俯仰角和偏航角指令。

2.2 導納控制

導納控制提供了一種飛行器與外界的物理交互方式，即一個位置控制的機械系統，它可以通過感知外部的力來生成一個運動軌跡，調節飛行器的運動，實現任意的交互行為。因此，從機可以看成一個被動運動的質點。這種力和運動間的動態關系可以表示為

導納控制器可以表示為狀態空間方程形式，選取狀態量ξad=(IΛr,Ivr)和輸入量uad=可以得到：

2.3 位姿控制器設計

線性二次型調節器（LQR）其控制對象為線性系統，而性能指標為控制輸入和對象狀態組成的二次型函數，最優解具有統一的表達式，容易求得閉環形式的最優控制，且易于工程實現[19]。對于單個無人機本身則分別設計位置控制器和姿態控制器。

假設位置控制的狀態空間模型為

狀態量、輸入量和輸出量分別為

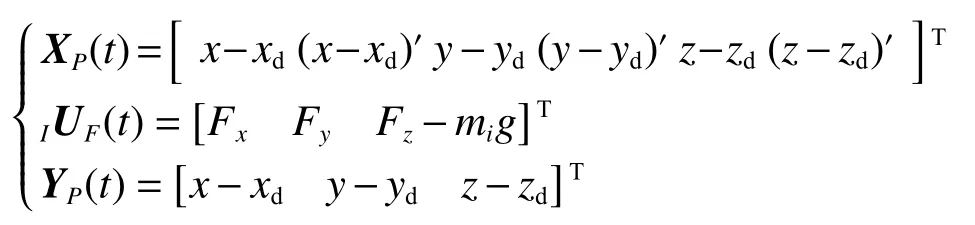
類似的，姿態控制的狀態空間模型為

其中狀態量XΘ(t)、輸入量BUM(t)和輸出量YΘ(t)分別表示為

定義LQR 的性能指標為

式中Q、R是對狀態變量和輸入量的加權矩陣。

求解二次型最優控制即找到狀態反饋控制律U(t),使得性能指標J取得極小值，可采用Ricatti 方程[28]：

可以得到

經過分析試驗選取使系統性能良好的位置和姿態控制器的Q、R分別為

3 仿真驗證

為了驗證本文提出方法的有效性，設計了基于Matlab/Simulink 環境下搭建雙無人機協同搬運的仿真，系統仿真參數如下：單架飛行器質量（mi）為2.12 kg，負載質量（mp）為1.06 kg，x軸/y軸轉動慣量（Ixx/Iyy）為10.52 kg·m2，z軸轉動慣量（Izz）為0.91kg·m2，重力加速度（g）為9.81m/s2，升力系數和阻力系數（kf/km）分別為3.07×10-5和5.33×10-7。

3.1 單架無人機位姿穩定控制仿真

對于主機和從機分別進行位姿穩定控制實驗，驗證LQR 控制器對于單架飛行器的控制效果，且由文獻[21]可知，單獨設計導納控制器不會影響從機內部回路的整體運動學。首先測試位置姿態控制器的性能，無人機初始位置前10 s垂直起飛至目標點進而到達期望位置點同時設定姿態期望為飛行軌跡如圖4所示，圖5為同步的姿態曲線。

圖4 位置控制的飛行軌跡

圖5 位置控制的姿態曲線

由圖4 和圖5 可見，采用LQR 控制器的無人機能夠迅速平穩地飛向目標點并懸停在目標點；與此同時，飛行器能夠保持姿態在很小的范圍內變化。所以LQR 控制器的穩定控制效果較為理想。

3.2 雙機協同位姿追蹤仿真

當雙機進行協同搬運任務時，通過仿真結果驗證控制策略的有效性以及控制器的控制性能。

考慮主機以及負載運動對從機的影響，并根據選取的連接關節，假定負載對從機的力作用于從機的質心。若沒有外力作用，則前述控制方案簡化為底層的位置姿態控制器，但是由于系統內外的干擾，會導致估計的力不為零，所以對于導納控制器設計一個控制“開關”，只有當估計的力高于某一閾值時，導納控制器啟動，反之，對于較小的力，導納控制器不啟動。

3.2.1 從機受瞬時負載力的仿真

選取從機剛度矩陣K=0，當從機x軸方向受到瞬時負載力時，導納控制器輸出響應以及從機估計的力響應如圖6 所示，圖7 和圖8 為相應主機和從機姿態響應。

圖6 從機x 軸響應

圖7 主機姿態曲線

圖8 從機姿態曲線

從機的運動依賴于外部受到的力，由于濾波器進行力估計需要收斂時間，如圖6，估計的力和實際的力之間存在延遲。且由于擾動力的存在，在導納控制器對力進行響應之前，飛行器已經開始運動。如圖7 和圖8 所示，當從機受到瞬時力，由于硬連接產生的相互作用，主機同時會受到負載的拉力，主機和從機姿態角都會出現一定程度的波動，但10 s 后主機和從機的姿態都恢復穩定，可以看出LQR 控制器能夠保證主從機姿態的穩定。

3.2.2 主從機連續軌跡追蹤仿真

對雙機協同搬運負載進行連續時間軌跡仿真，給定主機如式（1）的連續軌跡期望，主機和從機的三維軌跡曲線，即螺旋線軌跡如圖9 所示。圖10 和圖11 為追蹤螺旋線軌跡時相應主機和從機姿態響應曲線。

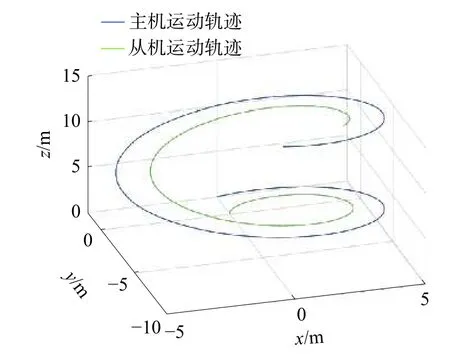
圖9 主機和從機螺旋線跟蹤軌跡曲線

圖10 主機姿態曲線

圖11 從機姿態曲線

結果表明，對于連續的螺旋線軌跡，從機能夠保證位置的穩定跟蹤。主機和從機與負載剛性連接，在三維空間能夠保持相對位置不變。圖10 和圖11 表明主從機在跟蹤螺旋線軌跡過程中，主機姿態角雖然會出現波動，但能夠快速保持穩定，從機由于被動力驅動，姿態角會出現持續的較小幅度的變化。總體來說，本文設計的控制方法，能夠實現雙機穩定地協同搬運負載的任務。

4 結論

本文對雙無人機協作搬運系統控制方案進行了研究。該方案在位置姿態控制器基礎之上采用卡爾曼濾波器估計施加在從機上的外力，并通過導納控制器根據受到的外力生成運動軌跡。實驗結果可以證明本文提出方案的有效性。在今后研究中，可以進一步開發力位混合控制策略，深入考慮分析風擾等外部干擾產生的問題，加強系統魯棒性，進而提升該系統執行困難任務的能力。