廣義離散時間系統的P-D 反饋控制器設計
任禎琴,李靜,李德光
洛陽師范學院 信息技術學院,河南 洛陽 471934
廣義系統是比正常系統更一般的動力系統,有著廣泛的應用背景。廣義系統大量出現在電力系統、能源系統、經濟系統、宇航系統和化學過程等描述中[1-4],這是因為實際應用中,廣義系統較一般系統可以用來描述系統更多的性能特征。隨著科學研究的深入,廣義系統被學術界廣泛關注,廣義離散時間系統理論已有了豐富的研究成果[5-7].
對于正常系統,反饋控制的研究已經趨于完善。但對于廣義系統來說,脈沖的存在可能引起系統不能正常運行甚至導致系統的損壞,這就需要所設計的控制器不僅要保證閉環系統是穩定的,而且是要正則化和因果的(連續系統無脈沖),即容許性。而P-D 反饋控制在這方面發揮了很大的作用,它是消除脈沖的一個很有效途徑,相關研究已取得了一些成果[8-14]。但由于P-D 反饋控制器在實際處理時的負面影響,很難使閉環系統達到穩定。然而隨著先進的生產設備和計算機的迅速發展,大大降低了這種負面影響,使得P-D 反饋具有很高的理論意義和工程實際應用價值。
本文針對廣義離散系統設計出一種簡單的PD 反饋控制器,突破了文獻[13]中輸出反饋控制器的局限性,使閉環系統更容易達到穩定,并消除了脈沖。
1 預備知識及問題描述
考慮如下的廣義離散時間系統:
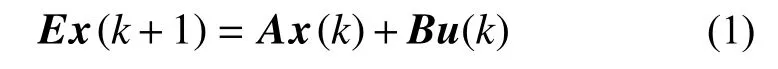
式中:x(k)∈Rn為狀態向量;u(k)∈Rr為輸入向量;E、A、B為具有適當維數的常數矩陣;E為奇異矩陣,滿足rank(E)<n。
定義1[15]若存在復數s0,使得det(s0E-A)≠0,那么稱式(1) 廣義離散時間系統是正則的。
本文假定廣義離散時間系統是正則且能穩定的。
定義2[15]若對任意復數z滿足degdet(zE-A)=rank(E),則稱廣義離散系統是因果的。
定義3[15]如果式(1)正則廣義離散時間系統是因果且穩定的,則稱系統是容許的。
定義4[15]如果存在P-D 反饋,使閉環系統成為正常系統,則稱廣義離散系統是能正常化的。
下面給出本文需要用到的相關引理。
引理1[15]式(1)廣義離散系統是容許的充要條件為:存在對稱矩陣X∈Rn×n滿足如下廣義Lyapunov 不等式:
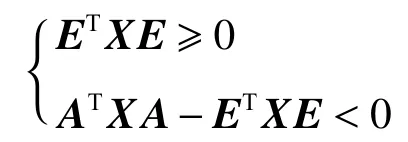
引理2[16]對于正常系統x(k+1)=Ax(k)+Bu(k),設性能指標函數為
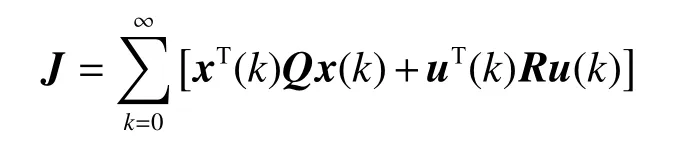
式中:Q為對稱半正定矩陣,R為對稱正定矩陣。系統滿足能穩定,能檢測,則最優狀態反饋控制器為
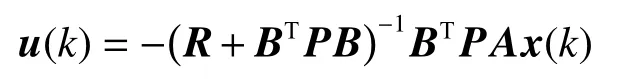
其中P為黎卡提方程
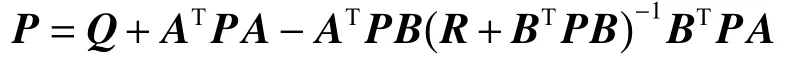
的對稱半正定解.
引理3[15]式(1)廣義離散系統是因果的充要條件為
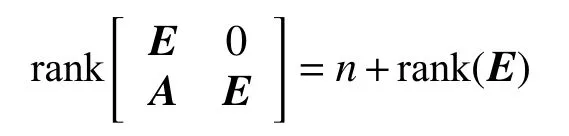
引理4[15]式(1)廣義離散系統是穩定的充要條件為:它的有限極點集合σ(E,A)是在復平面的單位圓內(用Ω(0,1)表示)。
引理5[15]式(1)廣義離散系統能穩定的充要條件為
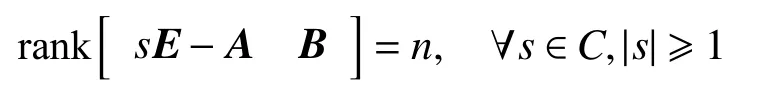
引理6[15]P-D 反饋保持了廣義系統的能穩定性。
為了研究的需要,我們要對系統進行正常化的分解。所謂正常化分解,就是通過線性變換將原系統分解為2 個子系統,其中1 個子系統是能正常化的,即轉化為正常系統,具體過程如下。
考慮式(1)廣義離散系統:
1)若系統是正則的,則一定存在非奇異矩陣Q1、P1,使得
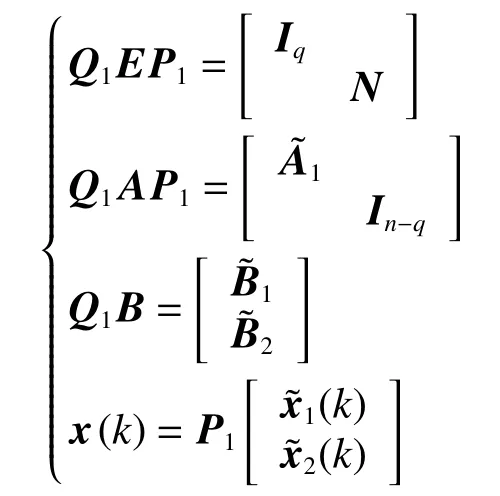
式中:N為冪零矩陣,那么,式(1)廣義離散系統將改寫為
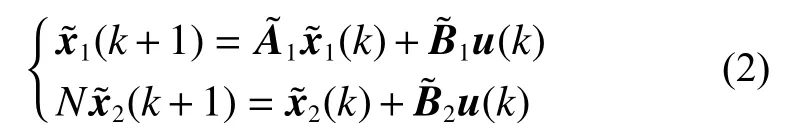

則式(2)改寫為

式(2)可改寫為
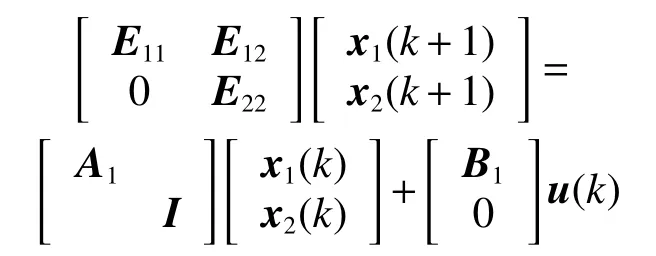
即
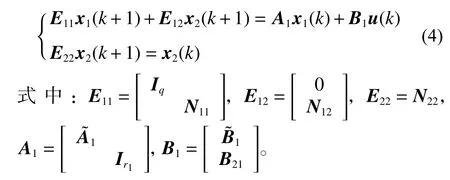
正文中已經得到x2(k)=0,則式(4)可改寫為
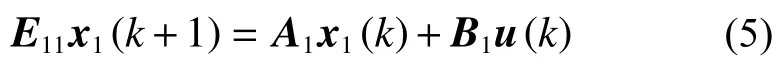
下面證明若原式(1)廣義離散系統是能穩定的,則式(5)是能穩定的。由引理5,我們只需證明?s∈C,|s|≥1,行滿秩,其中
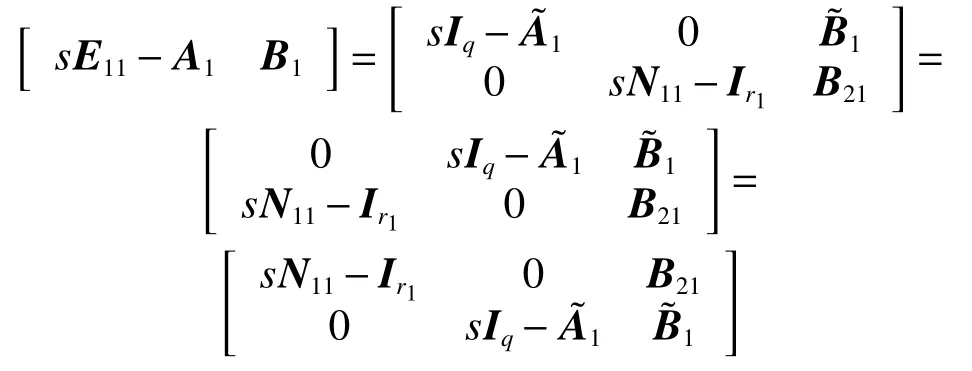
首先N11是冪零矩陣,則是行滿秩的;原系統是能穩定的,則

將式(1)廣義離散系統進行正常化分解得

由式(6)中E22x2(k+1)=x2(k)得:
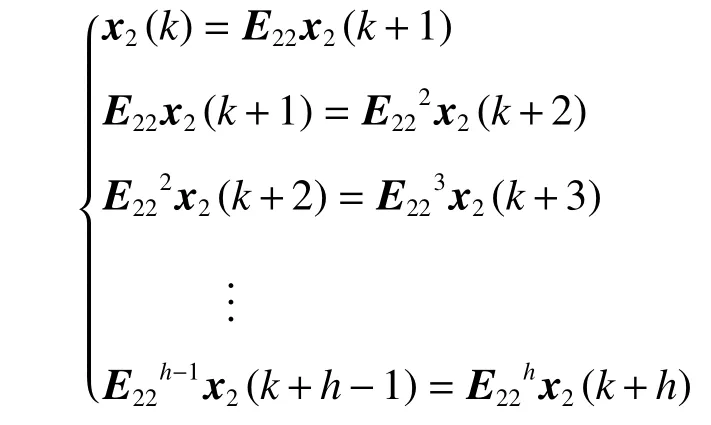
將式(7)左右分別相加并相消得:
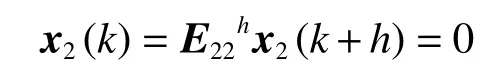
所以式(6)可改寫為
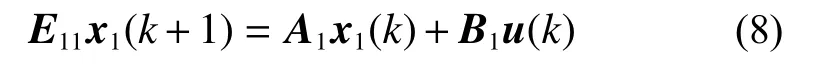
由于式(8)是能正常化的,則一定存在P-D反饋:
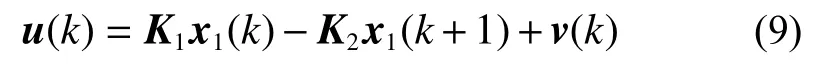
使得閉環系統
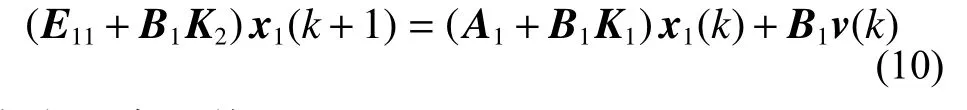
成為正常系統。
我們選擇一個合適的K2使得
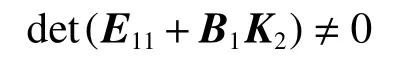
2 P-D 反饋控制器的設計
本文的主要研究工作是設計一個P-D 反饋控制器,使得閉環系統是容許的。首先對原系統進行正常化分解,得到的子系統是能正常化的。在此基礎上,設計了一個P-D 反饋控制器。為了獲得控制器存在的充分條件,有如下定理。
定理1對于式(8),若存在P-D 反饋控制器式(9),使得閉環系統式(10)是容許的,條件是存在一個對稱正定矩陣Y,合適維數的矩陣Z滿足線性矩陣不等式(11):
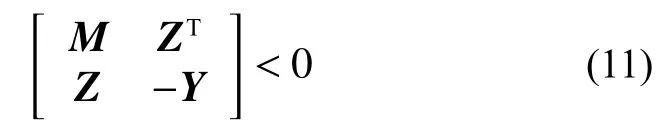
式中:

證明: 由于det(E11+B1K2)≠0,則E11+B1K2可逆,顯然滿足引理1 中的ETXE≥0,即(E11+B1K2)TY(E11+B1K2)≥0,又有
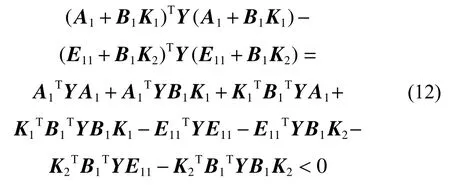
令

式(12)將改寫為
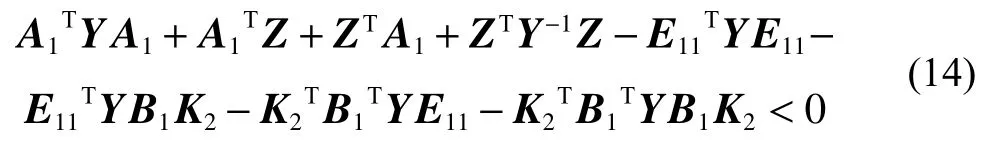
利用schur 補引理[16],我們可以將式(14)轉化為線性矩陣不等式(11),其中:證畢。
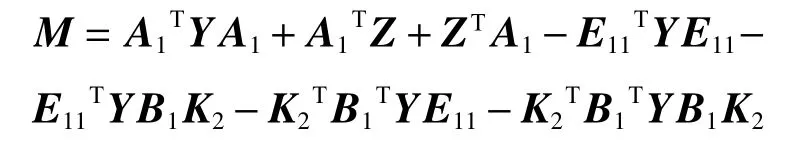
通過Matlab 求解式(11),可以求得Y、Z的值[17]。
接下來利用式(13)和Y、Z的值來求得K1的值,這就需要利用廣義逆的理論[18]。
由式(13)可得

下面我們利用廣義逆的知識來求得K1的值,先將B1進行滿秩分解,記為B1=MN,其中M列滿秩,N行滿秩。若式(15)有解,則K1=NT(NNT)-1(MTM)-1MTY-1Z是式(14)的極小范數解;若式(15)無解,則K1=NT(NNT)-1(MTM)-1MTY-1Z是式(11)的極小范數最小二乘解,也稱最佳逼近解,需要進一步驗證式(11)。
對于式(10),我們可以將其變形為正常系統:
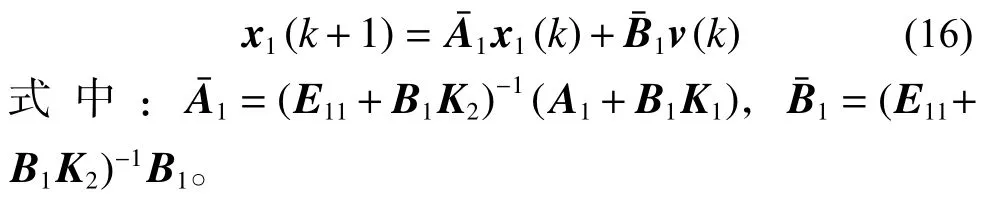
對于式(16),定義性能指標函數為
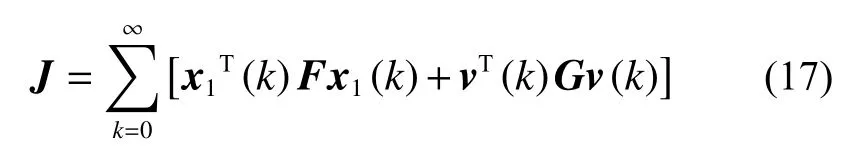
式中:F為對稱半正定矩陣;G為對稱正定矩陣,且滿足能檢測。
再由正常化分解的方法以及引理5 和引理6,可以得到式(16)是穩定的。運用引理2,就可以得到式(16)的狀態反饋控制器為
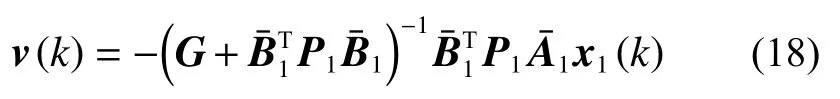
并使得閉環系統是穩定的。其中P1是代數黎卡提方程的對稱半正定解:
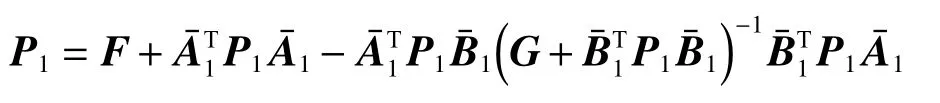
由此,將式(18)代入P-D 反饋控制器式(9),得到原系統式(1)的P-D 反饋控制器為
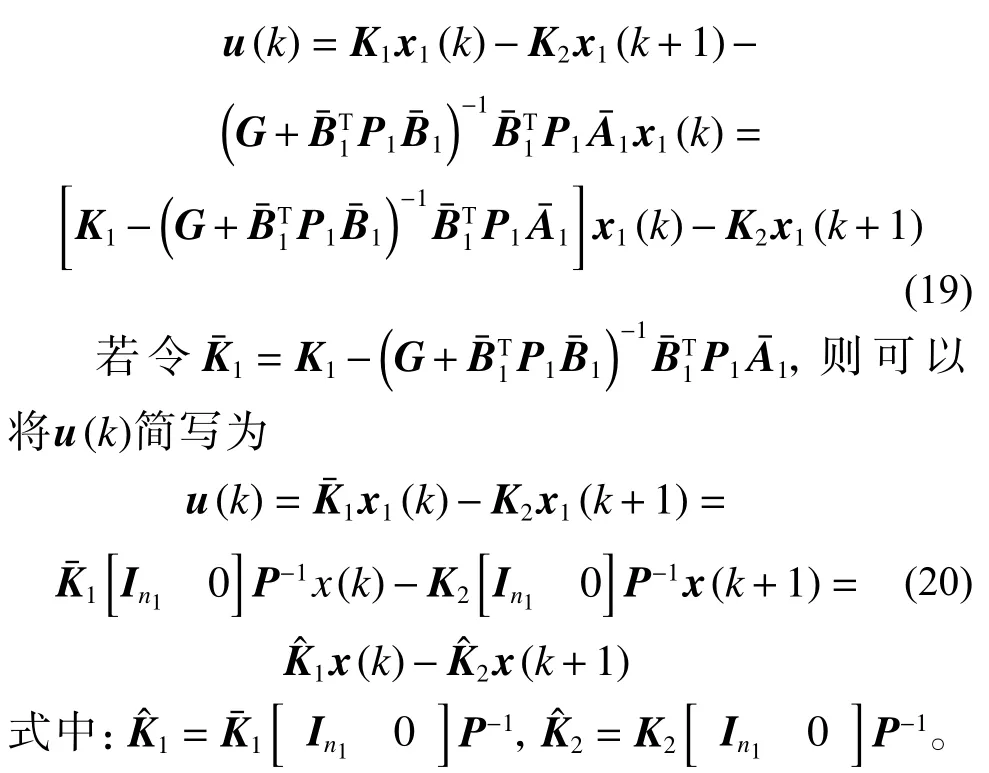
將式(20)代入式(1)可得閉環系統為
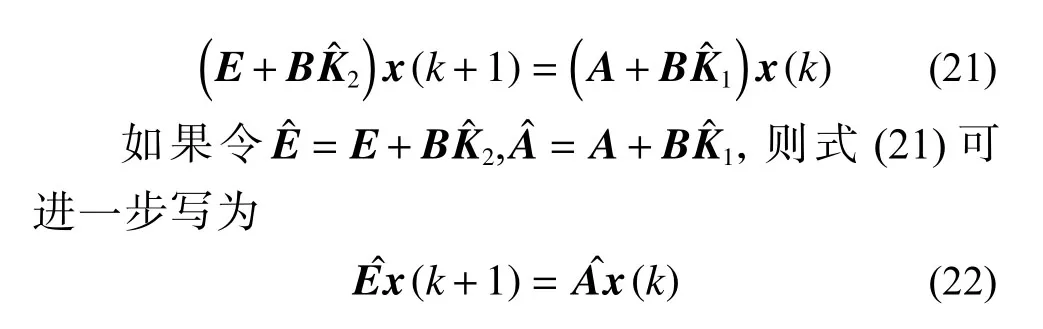
本定理得到的是P-D 反饋控制器存在的充分條件,而引理1 給的是廣義離散系統容許的充要條件,這是因為本定理中為了利用Matlab 中的LMI 工具箱,規定Y是對稱正定矩陣,而引理1 中的X是對稱矩陣,這是在以后的研究中需要改進的地方。在定理1 的基礎上,給出式(1)廣義離散系統的P-D 反饋控制器設計的定理。
定理2對于式(1),存在一個對稱正定矩陣X和合適維數的矩陣Z滿足下面線性矩陣不等式:
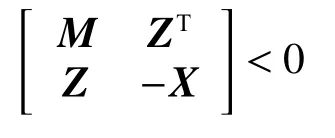
式中:
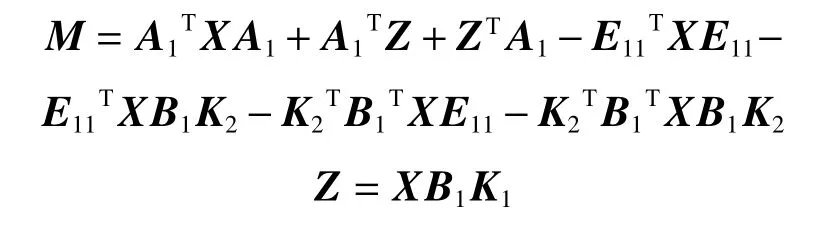
則一定存在一個P-D 反饋控制器如式(20),使得閉環系統(22)是容許的。
利用定理2 時,我們需要先將原系統式(1)進行正常化分解,可以借助計算機。下面利用一個數值算例來說明本文設計方法的正確性和有效性。
3 數值算例
考慮形如式(1)的廣義離散系統:
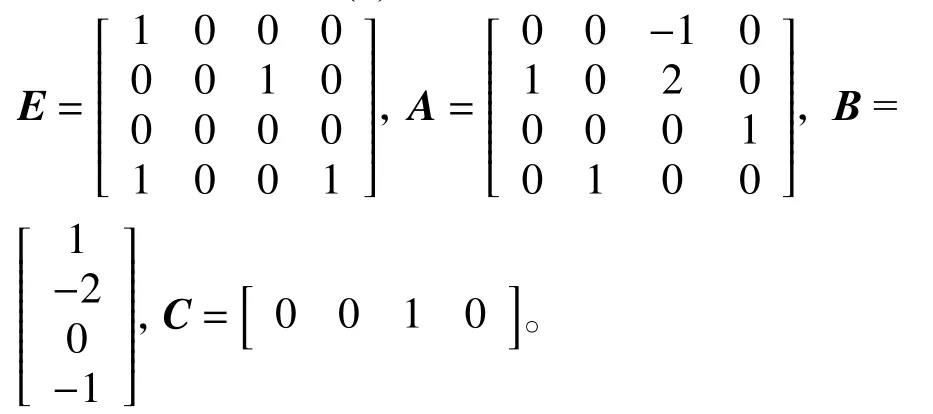
首先有det(2E-A)≠0,說明系統是正則的;又有rank滿足引理5中的條件,所以系統滿足能穩定性。

通過計算得式(20)中的增益矩陣為

閉環系統式(17)的系數矩陣為

下面通過驗證說明在設計的控制器下,所得的閉環廣義系統是容許的。
綜上,我們驗證了所得的閉環廣義系統是容許的。這一結果說明了本文通過對原系統進行正常化分解所得到的P-D 反饋控制器是有效的。
圖1 是輸出響應曲線,從圖中可以看出利用現代控制理論和變量替換法使得閉環系統是容許的、穩定的。
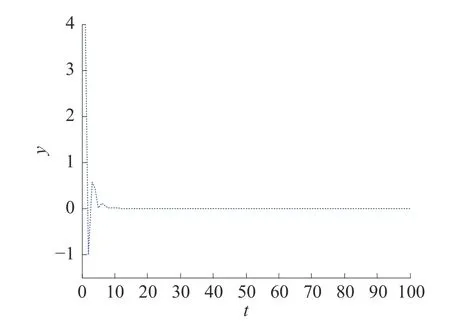
圖1 輸出響應曲線
4 結論
廣義系統存在脈沖行為,會導致系統不能正常運行甚至崩潰。而P-D 反饋控制器是消除脈沖的一個很好方法,于是本文通過引入了P-D 反饋控制器來消除脈沖,從而使得系統是穩定的、容許的,并給出了閉環系統容許的條件。
1)通過對式(1)系統正常化分解推導出子系統能正常化。
2)給出了P-D 反饋控制器存在的條件,使得式(10)系統是容許的,并且得到了相應的LMI 條件。為了求解方便,利用Matlab 中的LMI 工具箱,但是要求里面矩陣是對稱矩陣,這是在以后的研究中需要解決的問題。
3)給出了式(1)系統控制器存在的條件。

