基于MATLAB的液壓伺服系統位置控制仿真分析

劉　銳

基于MATLAB的液壓伺服系統位置控制仿真分析

劉銳

(湖南信息職業技術學院，湖南 長沙 410200)

在分析IGV系統的組成和原理的基礎上，搭建了IGV系統液壓模擬試驗臺。根據液壓模擬試驗臺相關部件的參數，在Simhydraulics中搭建了仿真模型。用最小二乘參數辨識方法對所搭建的仿真模型進行系統辨識，得出系統的傳遞函數。根據系統傳遞函數的特性，設計了優化的PI控制器，并利用MATLAB進行仿真分析。結果表明，所設計的控制器能夠保證液壓伺服系統具有良好的位置跟隨性，并且具有一定的抗干擾性能，滿足實際工作條件。

液壓伺服系統；位置控制；PI控制器；IGV

1　引言

隨著現代工業的迅速發展，電液比例控制已經廣泛應用于能源電力、機械制造和冶金工業中精度要求較高的工程實踐里。在上述這些行業中應用的很多液壓設備都能實現較高的位置控制精度。例如，在用于燃氣—蒸汽聯合循環的重型燃氣輪機中，為了擴大壓氣機的穩定工作范圍，提高聯合循環效率，常常在壓氣機的第一級動葉之前設計一列進口可轉導葉(Inlet Guide Vane, IGV)。液壓伺服系統位置控制的快速、準確和穩定是IGV系統正常工作的必要條件。由于采用由電液比例閥控制液壓缸組成的閉環控制系統能夠實現精度要求較高的位置控制，因此對其進行研究有著重要的現實意義。

針對GE公司PG9351FA型和三菱公司M701F4型燃氣輪機中的IGV液壓調節系統，在Simhydraulics仿真平臺上搭建了物理模型。利用參數辨識的方法對物理模型進行系統辨識，得到系統的傳遞函數，利用MATLAB/Simulink進行仿真分析，研究優化的PI控制器，并對系統進行校正。

2　系統的組成和原理

在PG9351FA的IGV系統中，每一個IGV葉片的頂部都安裝了一個小齒輪。這些小齒輪的轉動由兩個半圓的齒條帶動；齒條的動作由油動機HM3-1來操縱。這樣，就可以通過油動機的動作來改變IGV的安裝角。

如圖1所示，燃機啟動時，來自OH-4的高壓液壓油經過濾器FH6-1后流向伺服閥90TV-1和進口可轉導葉遮斷閥VH3-1。由于跳閘油在啟動轉速繼電器14HT動作前(>15%轉速動作)是無壓狀態，所以遮斷閥VH3-1在左邊彈簧力的作用下處于左位。液壓油經VH3-1進入油動機HM3-1的油缸活塞下腔室。活塞上腔室經VH3-1接通回油管路OD。此時，油動機活塞移到頂部，使IGV處于初始狀態的最小開度，即28.5°。

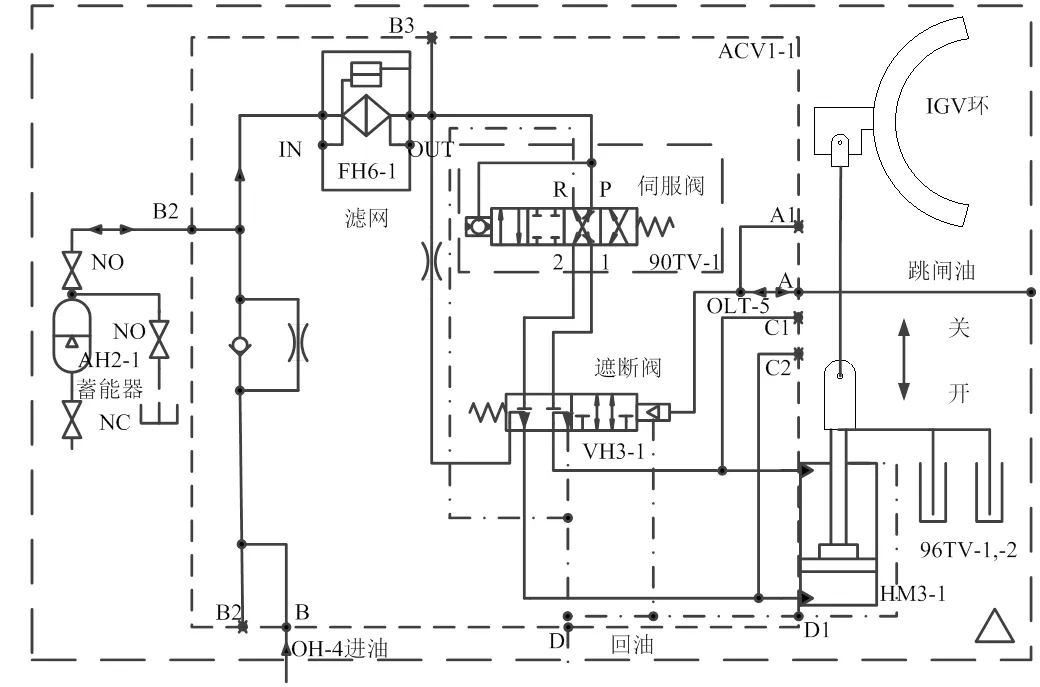
圖1　壓氣機IGV系統圖

當機組在變頻啟動裝置的牽引下啟動并使14HT動作時，形成跳閘油壓，推動VH3-1閥向左移動并使該閥處于右位。這時，將液壓油OH-4接通伺服閥90TV-1和油動機之間的液壓油路，使IGV處于可調整狀態。位置信號LVDT(96TV-1，-2)用于IGV開度的調節反饋[1]。

將閥控液壓缸簡化，所設計的IGV液壓調節系統模擬平臺如圖2所示。圖2中，IGV位置調節系統包括IGV系統液壓源、三位四通伺服閥、工作液壓缸和油箱等，系統工作液壓缸油壓為3～4MPa。液壓負載輸出系統包括負載系統液壓源、三位四通伺服閥、負載液壓缸、油箱、力傳感器和位移傳感器等，系統負載液壓缸油壓為1～2 MPa。

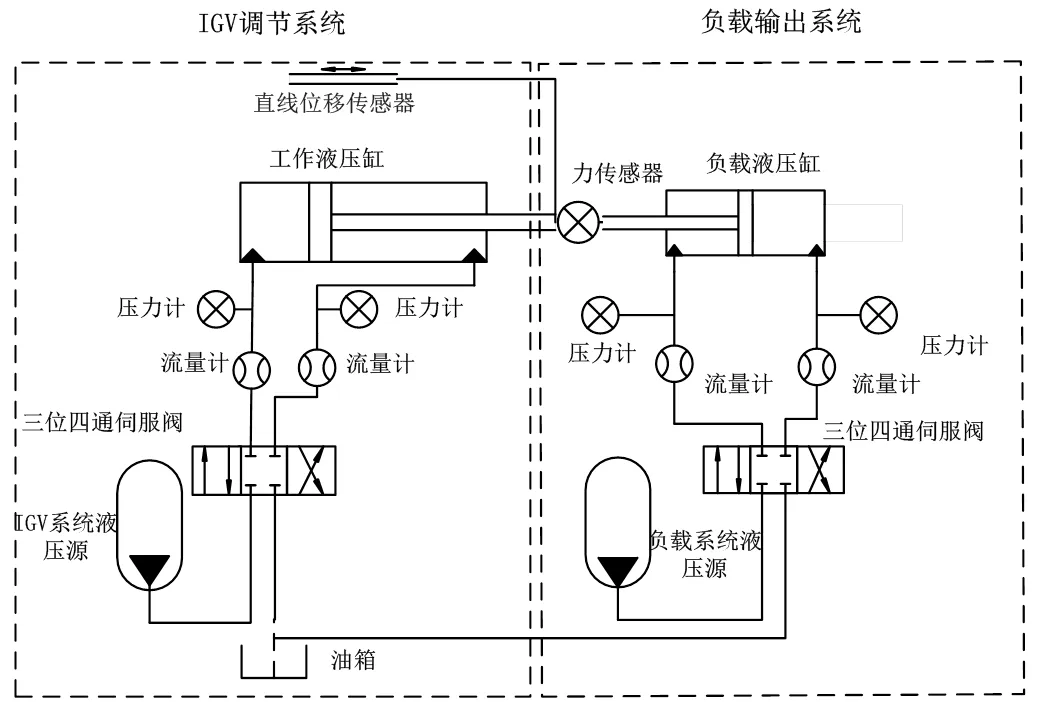
圖2　IGV液壓調節系統模擬平臺

3　基于Simhydraulics建立系統物理模型

3.1　系統的主要參數

將工作油泵的油壓設定為3MPa；雙作用液壓缸的行程是200mm；彈簧質量阻尼系統中：kg，1000N/m，N/(m/s)。

3.2　系統的物理模型

通過對圖2的分析，在Simhydraulics中建立IGV液壓調節系統模擬平臺的仿真模型，如圖3所示。

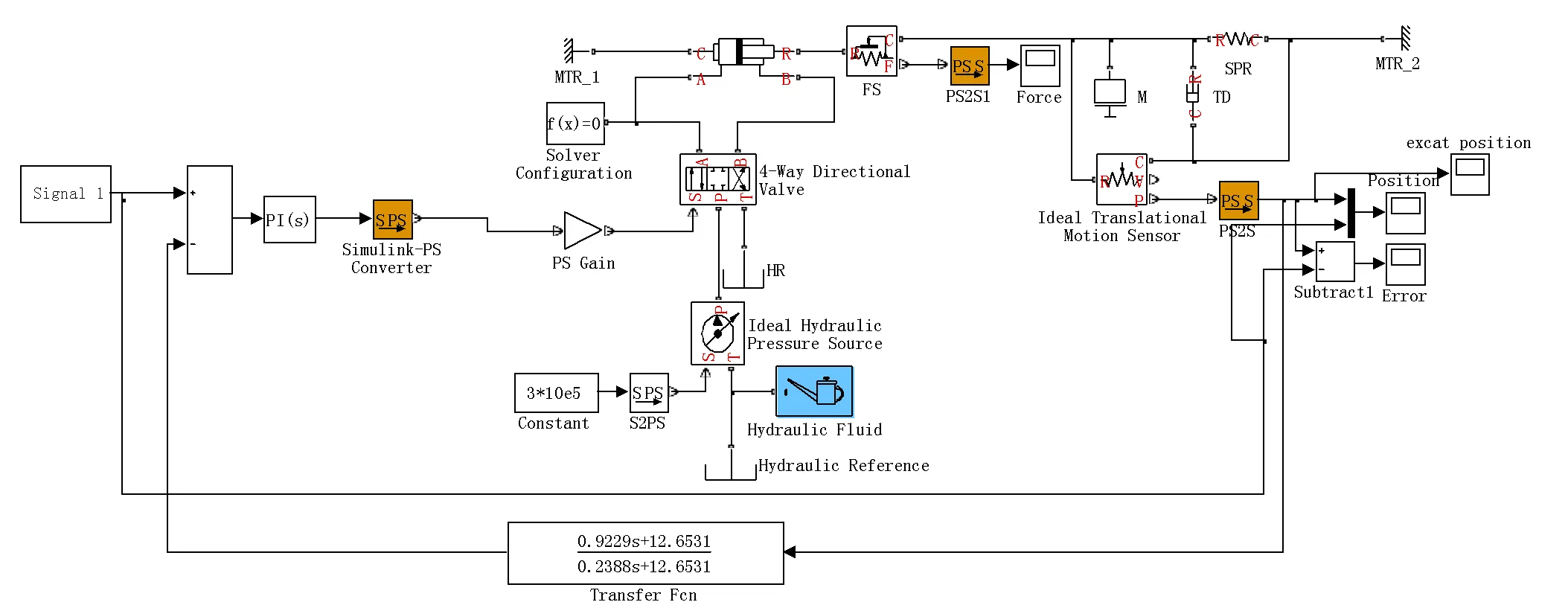
圖3　IGV液壓調節系統模擬平臺仿真模型

整個物理模型由輸入部分、控制部分、執行部分、數據采集和顯示部分組成。其中，輸入部分模擬的是IGV系統實際工作過程中的指令信號；控制部分采用的是PI控制器，通過三位四通換向閥控制雙作用液壓缸的行程位置；執行部分是一個雙作用液壓缸，液壓缸的負載由一個彈簧質量阻尼系統來模擬；數據采集和顯示部分使用位移傳感器，對雙作用液壓缸的位置進行測量，采用示波器顯示數據，可分別顯示指令位置、實際位置以及實際位置與指令位置的誤差三項內容。

3.3　閥控液壓缸的系統辨識

為了分析系統的行為特性、理解系統的運動規律、設計系統的控制策略，通常需要了解系統的數學模型。多數情況下，系統的數學模型并不可知，或者數學模型的參數會隨著系統運行環境的變化而變化。通過測取系統在某些輸入信號作用下的輸出響應，或者是記錄正常運行的輸入輸出數據，經過必要的數據處理和數學計算，估計出系統的數學模型。利用系統辨識的方法建立的數學模型一般是系統輸入輸出特性在某種準則意義下的一種近似，近似的程度取決于人們對系統先驗知識的認識和對數據集合性質的了解以及選用的辨識方法[5]。

對系統辨識的方法有很多，其中應用最廣泛、辨識效果良好的是最小二乘辨識法。應用最小二乘法對系統模型參數進行辨識的方法有離線辨識和在線辨識兩種。離線辨識是在采集到系統模型所需全部輸入輸出數據后，用最小二乘法對數據進行集中處理，從而獲得模型參數的估計值。根據式(2)搭建物理仿真模型，可以采集到系統的輸入輸出數據，采用最小二乘法進行離線辨識，得到系統的傳遞函數，如圖4所示。

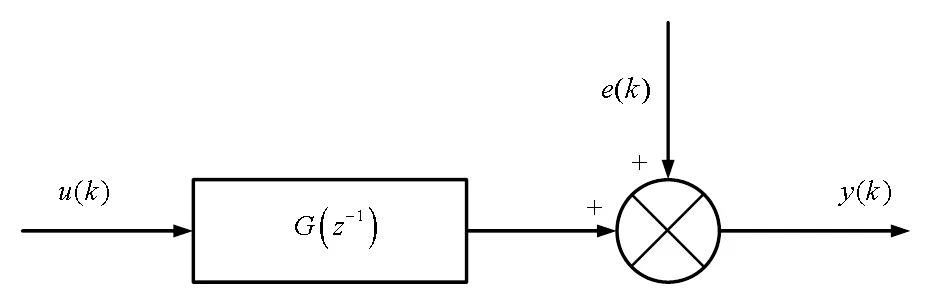
圖4　SISO系統結構圖

系統的離散傳遞函數為：

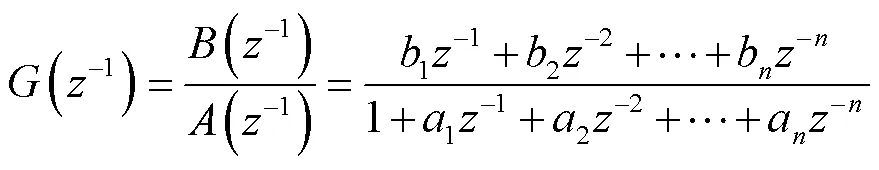
系統輸入輸出的關系為：

結合(1)式和(2)式可以得到：

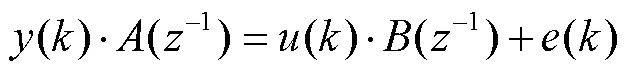
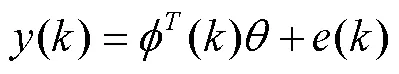
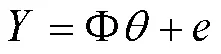
其中：

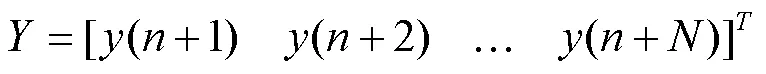
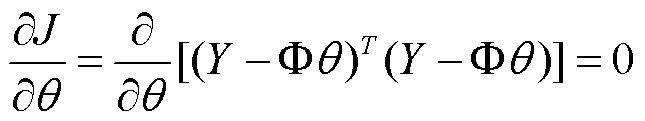
那么，由此得到最小二乘估計為：

根據最小二乘參數辨識法，系統的傳遞函數為：

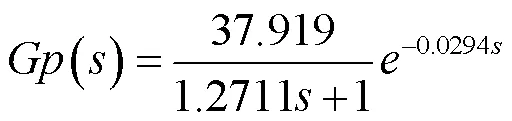
4　優化PI控制器及系統仿真分析

4.1　設計優化PI控制器

系統控制結構如圖5所示。

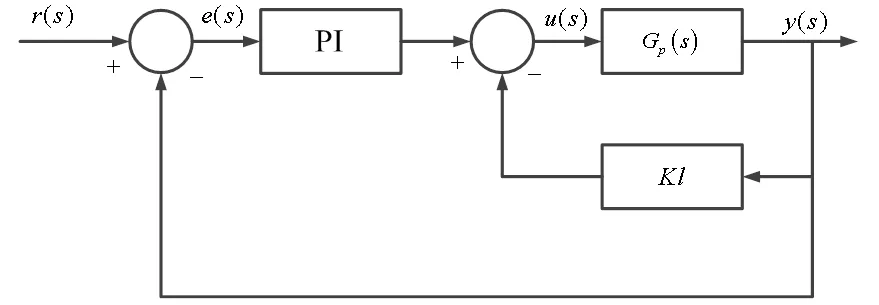
圖5　系統控制結構圖

在普通PI控制系統中加入內層反饋，根據自動控制原理相關知識，等效系統傳遞函數為：

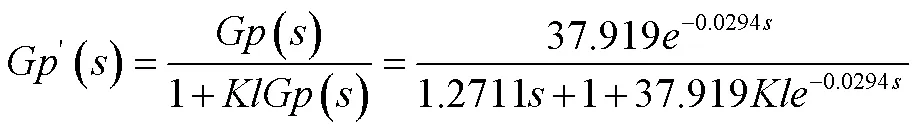
分母用泰勒級數展開：

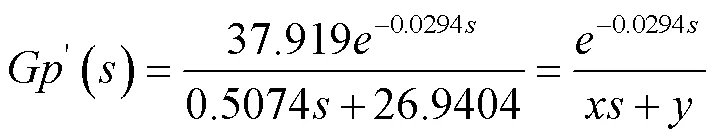
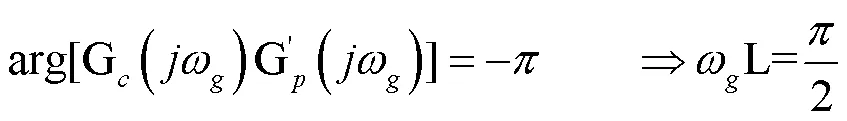
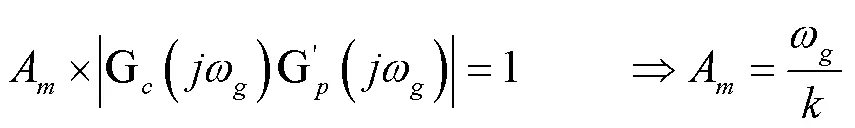
結合以上的分析，所設計的PI控制器為：

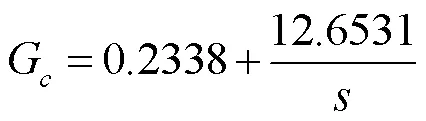
將圖5變簡化為圖6所示的結構：

4.2　系統仿真分析

設定仿真時間為20 s，選擇求解器ode14x。

仿真結果顯示：當IGV系統的指令位置如圖8所示的時候，根據圖7所示的誤差曲線可以看出，系統的超調量為0，誤差小于3%，滿足系統的要求。

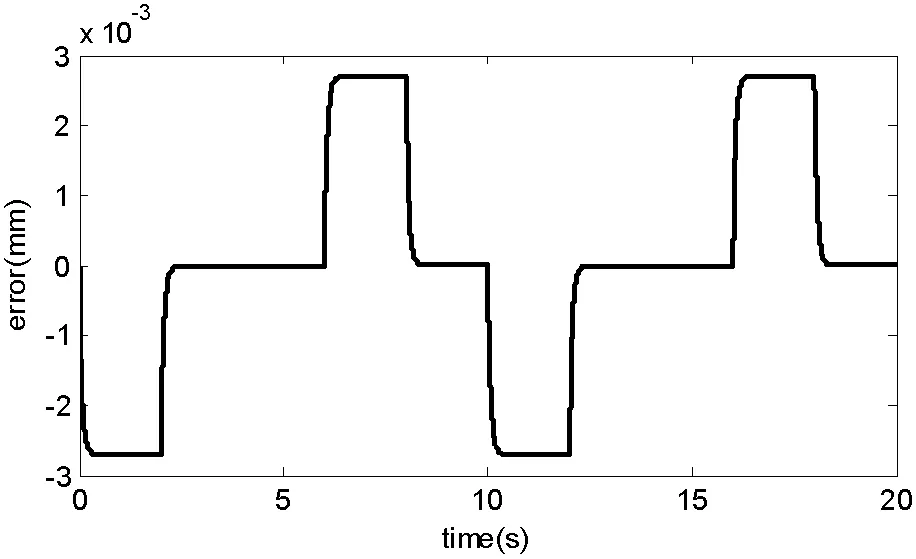
圖7 IGV系統模擬工況下的誤差

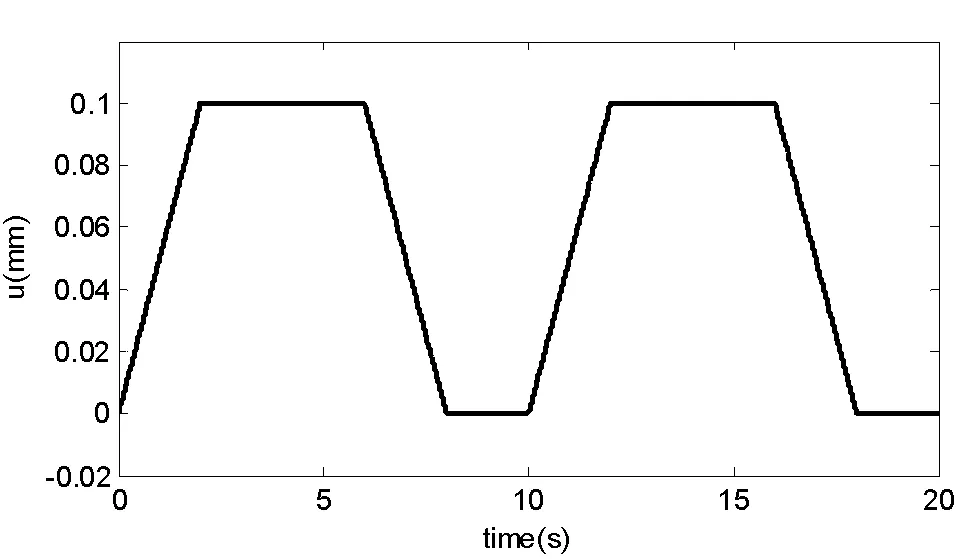
圖8　IGV系統模擬工況

系統的階躍響應表示系統的抗干擾性能。當系統輸入為幅值0.1的階躍信號時，相應誤差曲線的和響應曲線如圖9和圖10所示。

從圖9和圖10可以看出，系統具有相對較好的抗干擾特性。系統在受到突發擾動時能夠快速地回到穩態，并且穩態誤差為0。

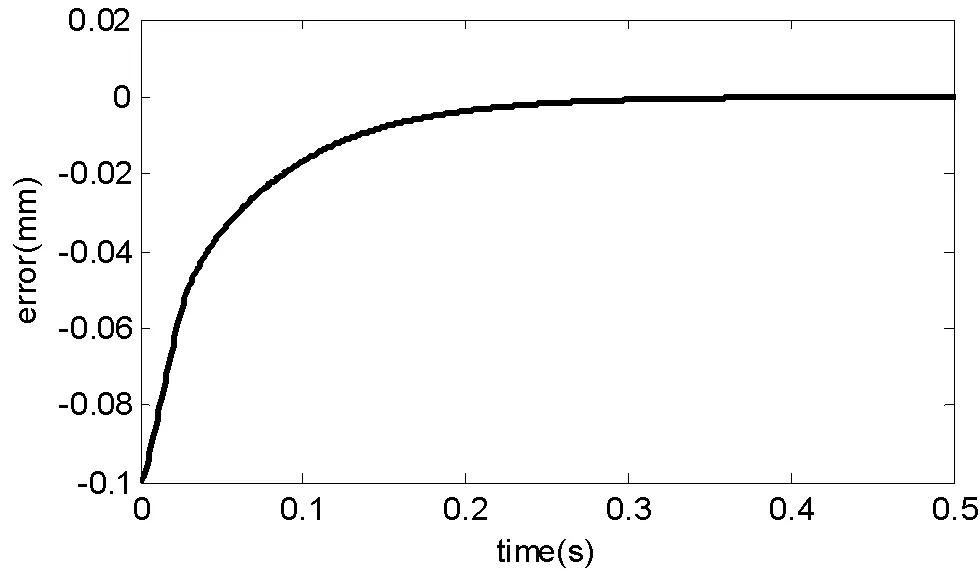
圖9　IGV系統仿真模型階躍響應誤差

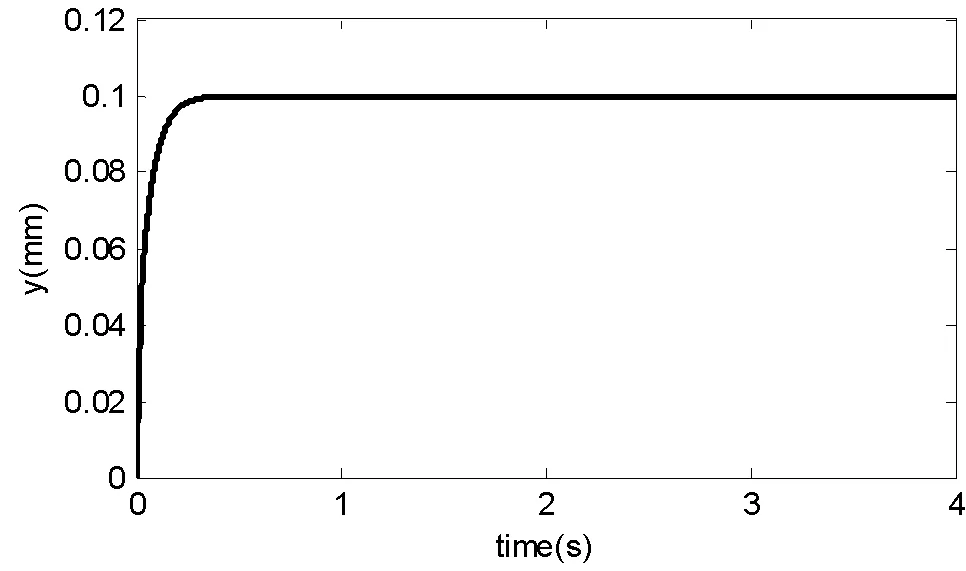
圖10　IGV系統仿真模型階躍響應

5　結論

在分析GE公司PG9351FA型和三菱公司M701F4型燃氣輪機中的IGV液壓調節系統的基礎上，搭建了IGV系統液壓模擬實驗臺。目的是設計一個優化的PI控制器，從而提高液壓伺服系統的位置指令跟隨性。搭建了基于Simhydraulics的物理仿真模型，并利用最小二乘參數辨識的方法求得系統的傳遞函數。在此基礎上，設計了優化PI控制器。從仿真結果可以看出：在IGV系統工作指令的情況下，最大相對誤差不到3%；系統在干擾存在的情況下(采用階躍信號模擬系統的干擾)，穩態誤差為0，超調量為0，上升時間為0.1270 s。系統的性能完全符合實際工作要求。

[1] 孫益科. PG9351FA型燃氣輪機進口可轉導葉的控制[J]. 制冷空調與電力機械,2008,29(5):78-82,85.

[2] 趙士杭.燃氣輪機結構[M].北京:清華大學出版社, 1983.

[3] 王春行.液壓控制系統[M].北京:機械工業出版社, 2011.

[4] 清華大學熱能工程系.燃氣輪機與燃氣:蒸汽聯合循環裝置(上)[M].北京:中國電力出版社, 2007:56-95.

[5] 蕭德云.系統辨識理論及應用[M].北京:清華大學出版社,2014.

[6] ZHAO Y G, JIA L, CAI W J. The system identification and PID auto-tuning for unstable processes[C]//2008 3rd IEEE Conference on Industrial Electronics and Applications. June 3-5, 2008, Singapore. IEEE, 2008: 176–180.

[7] SKOCZOWSKI S, DOMEK S, PIETRUSEWICZ K, et al. A method for improving the robustness of PID control[J]. IEEE Transactions on Industrial Electronics, 2005, 52(6): 1669–1676.

[8] WANG Y G, SHAO H H. Optimal tuning for PI controller[J]. Automatica, 2000, 36(1): 147-152.

Simulation analysis of hydraulic servo system's position control based on MATLAB

LIU Rui

(Hunan College of Information, Changsha, Hunan 410200, China)

Based on analyzing the composition and principle of the IGV (Inlet Guide Vane) system, in this paper, an IGV system's hydraulic simulator stand is built. According to the parameters of the relevant units in the hydraulic simulator stand, a simulation model was built in Simhydraulics. To estimate the unknown parameters of the system, the least square parameters estimation method was employed. As a result, we can get the transfer function of the plant. According to the characteristics of the system transfer function, the optimization of the PI controller is designed and simulated analysis with MATLAB. Results show that the optimized PI controller can help the hydraulicservosystem following the instruction very well. And with the optimized PI controller, this system has certain anti-interference performance, and can meet the actual working conditions.

hydraulicservosystem; position control; PI controller; IGV

TP273

A

2096–8736(2021)03–0028–05

劉銳(1992—)，男，江西贛州人，碩士研究生，工程師，主要研究方向為機電液一體化技術、機械設計及仿真分析。

責任編輯：陽湘暉

英文編輯：唐琦軍