周期驅(qū)動(dòng)系統(tǒng)的非平衡熱輸運(yùn)與熱力學(xué)幾何*
王子 任捷
(同濟(jì)大學(xué)物理科學(xué)與工程學(xué)院,聲子學(xué)與熱能科學(xué)中心,上海市特殊人工微結(jié)構(gòu)材料與技術(shù)重點(diǎn)實(shí)驗(yàn)室,上海 200092)
隨著對(duì)微納尺度系統(tǒng)的深入理解和實(shí)驗(yàn)技術(shù)的進(jìn)步,發(fā)生在這些小系統(tǒng)中的熱輸運(yùn)和能量轉(zhuǎn)換近期吸引了大量研究.不同于依賴(lài)靜態(tài)熱力學(xué)力(如溫差、電勢(shì)差等)的非平衡穩(wěn)態(tài)調(diào)控手段,受時(shí)間驅(qū)動(dòng)的非平衡非穩(wěn)態(tài)小系統(tǒng)具有特有的高可調(diào)性和普遍性,其研究同時(shí)具有基礎(chǔ)價(jià)值和應(yīng)用潛力.本文從幾何這一基本概念出發(fā),分析了熱力學(xué)幾何相(曲率)和熱力學(xué)距離這兩個(gè)關(guān)鍵物理量,以幾何的視角展現(xiàn)和分析近期關(guān)于受驅(qū)動(dòng)非平衡量子系統(tǒng)中輸運(yùn)調(diào)控和能量轉(zhuǎn)換途徑的熱力學(xué)研究.熱力學(xué)幾何不僅可以看作是這一大類(lèi)系統(tǒng)中非平凡輸運(yùn)和耗散的本質(zhì)起源,也同樣給我們提供了一種理論框架,給出對(duì)于系統(tǒng)輸運(yùn)和能量轉(zhuǎn)換的限制,同時(shí)也可以給出慢驅(qū)動(dòng)條件下量子熱機(jī)性能的通用優(yōu)化方式.這將在未來(lái)幫助理解非平衡量子多體系統(tǒng)所發(fā)揮的能量輸運(yùn)/轉(zhuǎn)換功能,也會(huì)為發(fā)現(xiàn)高性能(高效率、高功率、高可靠性)量子熱機(jī)提供新的設(shè)計(jì)思路.
1 引言
在現(xiàn)實(shí)生活中,宏觀的熱力學(xué)系統(tǒng),如熱機(jī)、制冷機(jī)、熱泵等發(fā)揮著重要作用,它們可以將一部分饋入的能量轉(zhuǎn)換為人們所需要的輸出能量.在此過(guò)程中,能量的轉(zhuǎn)換方向、轉(zhuǎn)換效率是衡量這些熱力學(xué)過(guò)程的重要參數(shù).而近些年來(lái),人們對(duì)于熱力學(xué)系統(tǒng)的研究集中到了非平衡的小系統(tǒng),通過(guò)納米制造和精確控制的實(shí)驗(yàn)手段,可以制備出承擔(dān)著各種熱力學(xué)任務(wù)的微納系統(tǒng).單布朗粒子熱機(jī)便是這方面的一個(gè)重要例子[1].在這樣的系統(tǒng)中,工作介質(zhì)往往具有較少的自由度和較小的空間尺度,它與熱庫(kù)進(jìn)行的能量交換過(guò)程充滿了大幅的漲落.如何利用隨機(jī)熱力學(xué)[2]的工具,來(lái)刻畫(huà)這些漲落過(guò)程中能流大小和能量轉(zhuǎn)換效率等物理量就成了一個(gè)重要問(wèn)題.另外,量子效應(yīng)也是研究低溫條件下隨機(jī)能量轉(zhuǎn)換過(guò)程所必須考慮的因素.一方面,量子熱機(jī)是構(gòu)造功能性量子器件的一個(gè)關(guān)鍵目標(biāo);另一方面,量子制冷機(jī)可以被用來(lái)在較冷的環(huán)境下進(jìn)一步對(duì)所要研究的系統(tǒng)進(jìn)行冷卻,從而凸顯其量子效應(yīng),使其可以承擔(dān)量子信息處理等任務(wù).研究表明,量子相干性[3]和壓縮態(tài)[4]可以被當(dāng)作一種資源,借以實(shí)現(xiàn)超出卡諾效率的熱機(jī).另外,在量子熱機(jī)中,熱流的漲落[5]和最優(yōu)相干性的尋找[6]也推動(dòng)了人們對(duì)量子熱機(jī)的理解.
時(shí)間驅(qū)動(dòng),正是小系統(tǒng)熱力學(xué)過(guò)程的一個(gè)重要調(diào)控手段,例如可以通過(guò)時(shí)間驅(qū)動(dòng)調(diào)控聲子系統(tǒng)中的拓?fù)渑c非互易性[7].如不依靠時(shí)間驅(qū)動(dòng),經(jīng)典的準(zhǔn)靜態(tài)過(guò)程雖然一般可以保證能量轉(zhuǎn)換效率最高,但它的長(zhǎng)時(shí)間功率卻趨向無(wú)窮小,因而很難被實(shí)際利用.靜態(tài)條件下工作的穩(wěn)態(tài)不可逆熱機(jī)雖然可以具有可以調(diào)節(jié)的功率和效率,但兩者間往往存在權(quán)衡關(guān)系和限制.因此最大功率下的效率極限[8-11]受到大量研究.與這些靜態(tài)框架相比,受到時(shí)間驅(qū)動(dòng)的小熱力學(xué)系統(tǒng)具有更大的可調(diào)空間,它們所發(fā)揮的功能和品質(zhì)參數(shù)可以通過(guò)設(shè)計(jì)特有的驅(qū)動(dòng)方案得到便捷的調(diào)節(jié)[12,13].
然而,相比穩(wěn)態(tài)系統(tǒng),時(shí)間驅(qū)動(dòng)的研究難度更大,一般性結(jié)論更少.特別地,在試圖直接對(duì)系統(tǒng)品質(zhì)參數(shù)進(jìn)行優(yōu)化時(shí),往往需要較大的計(jì)算量.尤其是在對(duì)多個(gè)品質(zhì)參數(shù)進(jìn)行多目標(biāo)優(yōu)化時(shí),最優(yōu)驅(qū)動(dòng)方案在不同優(yōu)化條件間還會(huì)出現(xiàn)相變等復(fù)雜現(xiàn)象[14].因而關(guān)于受驅(qū)動(dòng)小系統(tǒng)的普遍性概念和理論框架就顯得十分重要.幾何是物理系統(tǒng)的一種重要內(nèi)稟性質(zhì).它在小系統(tǒng)熱力學(xué)性質(zhì)的研究中也發(fā)揮著不可替代的作用.它可以描述非平凡幾何相(曲率)帶來(lái)的熱泵浦現(xiàn)象[15-18],也可以描述驅(qū)動(dòng)帶來(lái)的熱-功轉(zhuǎn)換過(guò)程[19,20]和驅(qū)動(dòng)帶來(lái)的額外熵的產(chǎn)生[21,22].另外,借助熱力學(xué)幾何的概念,人們可以利用熱力學(xué)度規(guī)[23,24],對(duì)能量轉(zhuǎn)換中的功率、效率和穩(wěn)定性等品質(zhì)參數(shù)進(jìn)行優(yōu)化[25,26].
本文關(guān)注于受周期性驅(qū)動(dòng)的小量子系統(tǒng)中,時(shí)間驅(qū)動(dòng)對(duì)于熱輸運(yùn)和熱-功轉(zhuǎn)換的調(diào)節(jié)作用.本文將介紹受驅(qū)動(dòng)熱力學(xué)系統(tǒng)中,幾何相(曲率)和熱力學(xué)距離的概念,它們分別代表了驅(qū)動(dòng)的可逆部分和不可逆部分.在此框架基礎(chǔ)上,本文分別介紹幾何相熱泵浦效應(yīng),以及熱力學(xué)幾何在描述熱機(jī)工作過(guò)程的作用.最后,本文介紹基于幾何方法提出的優(yōu)化方法和權(quán)衡關(guān)系.值得注意的是,由于各方面的限制,本文所介紹分析的內(nèi)容不具備絕對(duì)的完整性,而僅以近期的一些代表性研究工作為例向讀者展現(xiàn)這一新穎的研究方向.
2 周期性驅(qū)動(dòng)量子輸運(yùn)中的幾何相與距離
在周期驅(qū)動(dòng)熱力學(xué)系統(tǒng)中,幾何相和熱力學(xué)距離作為兩個(gè)重要概念,為我們提供了一種統(tǒng)一描述經(jīng)典/量子系統(tǒng)的理論框架.在幾何上,在一個(gè)可以定義任意兩點(diǎn)距離的空間中,可以使用Riemann空間中的度規(guī)來(lái)描述相近兩點(diǎn)間的距離.此無(wú)窮小距離沿著曲線的積分就是此路徑首尾兩點(diǎn)間的距離.在一個(gè)非平坦的空間中,一個(gè)矢量途經(jīng)一條閉合路徑進(jìn)行平行移動(dòng),其末了矢量與初始矢量間的夾角被稱(chēng)為和樂(lè)(holonomy)角,它即是幾何相的數(shù)學(xué)含義.一個(gè)光滑空間中,此和樂(lè)角可以通過(guò)路徑上幾何聯(lián)絡(luò)的線積分得到.從另一個(gè)角度,聯(lián)絡(luò)本身定義了曲面上向量平行移動(dòng)的方式,它使我們可以把不同位置處切空間內(nèi)的向量進(jìn)行比較.
在物理上,這些數(shù)學(xué)概念也有對(duì)應(yīng)的意義.開(kāi)放系統(tǒng)內(nèi)熱泵浦、功轉(zhuǎn)換等過(guò)程中,幾何相描述了經(jīng)由一個(gè)絕熱驅(qū)動(dòng),系統(tǒng)分布在回到其初始狀態(tài)時(shí),額外累積定向轉(zhuǎn)移熱量/功的多少[15].它可以由參數(shù)空間內(nèi)局域的幾何聯(lián)絡(luò)的積分得到.描述能量流(功/熱)的幾何聯(lián)絡(luò)可以類(lèi)比孤立量子系統(tǒng)中的Berry 聯(lián)絡(luò),它在驅(qū)動(dòng)路徑上的投影給出了在此參數(shù)點(diǎn)進(jìn)行一個(gè)微小絕熱驅(qū)動(dòng)所引起的額外熱流泵浦/功輸出.另外,若驅(qū)動(dòng)速度較小,但并非完全絕熱,則熱力學(xué)距離則描述了驅(qū)動(dòng)過(guò)程中引起的耗散大小[23].相近參數(shù)點(diǎn)間的熱力學(xué)距離可以定義出一個(gè)參數(shù)空間中的度規(guī).這樣的物理圖像如圖1所示.接下來(lái),我們給出具體的分析和推導(dǎo).
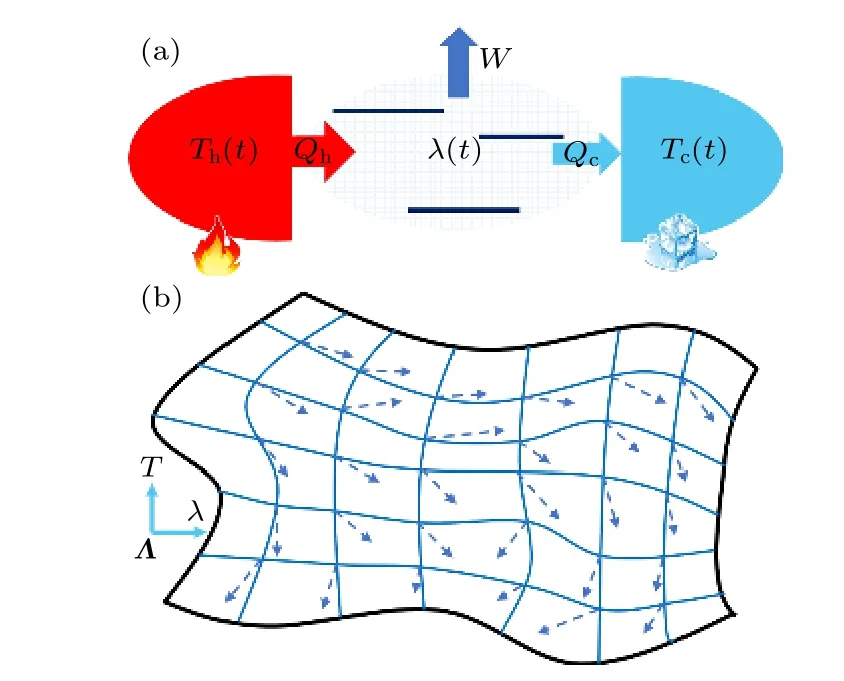
圖1 周期性驅(qū)動(dòng)非平衡量子輸運(yùn)和其中幾何性質(zhì)的示意圖 (a) 非平衡量子系統(tǒng)示意圖.量子系統(tǒng)由一個(gè)包含多個(gè)能級(jí)的系統(tǒng)來(lái)表示,它可以與多個(gè)熱庫(kù)相連.熱庫(kù)溫度(Th和Tc)和系統(tǒng)參數(shù) (λ) 都被含時(shí)地驅(qū)動(dòng).由此,可以產(chǎn)生系統(tǒng)與熱庫(kù)間的熱量交換(Qh和Qc)以及系統(tǒng)的功輸出(W).(b) 此非平衡量子系統(tǒng)在參數(shù)空間(Λ ≡(T,λ))中的幾何性質(zhì).曲線坐標(biāo)系表現(xiàn)出非均勻的熱力學(xué)距離,而各點(diǎn)的箭頭表示幾何聯(lián)絡(luò).幾何聯(lián)絡(luò)在幾何上對(duì)應(yīng)平行移動(dòng)一個(gè)微小參數(shù)時(shí)帶來(lái)的和樂(lè)(holonomy)角.熱力學(xué)距離定義了一個(gè)具有度規(guī)的黎曼曲面Fig.1.A scheme of periodically driven nonequilibrium quantum transport and its geometry.(a) A diagrammatic nonequilibrium quantum system.The middle quantum system is illustrated by a multi-level system,which is coupled with several thermal reservoirs.The temperature of reservoirs (Th and Tc) and the mechanical parameter of the system (λ) are simultaneously and periodically modulated.The heat exchange (Qh and Qc) and work output(W)are thus generated.(b) The geometry of this nonequilibrium quantum system in the space of parameters(Λ ≡(T,λ)).The curvilinear coordinate is adopted to show the inhomogeneous thermodynamic distance and the local vectors are for the geometric connection,as derived in the main text.Geometrically,the geometric connection is the holonomy angle during an infinitesimal parallel transport and the thermodynamic distance between neighboring points defines a Riemannian space with endowed metric.
假設(shè)作為工作媒質(zhì)的系統(tǒng)與周邊熱庫(kù)之間的耦合較弱,則根據(jù)開(kāi)放量子系統(tǒng)的理論,可以在波恩-馬爾可夫近似下,等效地使用量子主方程來(lái)描述粗粒化后系統(tǒng)的演化.若再進(jìn)一步假設(shè)旋轉(zhuǎn)波近似,則可以將此量子主方程簡(jiǎn)化為具有全正定且保密度矩陣跡(completely positive trace preserving,CPTP)的Lindblad 形式[27]:


假設(shè)在驅(qū)動(dòng)過(guò)程中,熱庫(kù)的溫度T和系統(tǒng)的參數(shù)λ被驅(qū)動(dòng),它們的驅(qū)動(dòng)形式為:Λ(t)=(T(t),λ(t))T.這里,上標(biāo) T 表示轉(zhuǎn)置操作.根據(jù)隨機(jī)熱力學(xué)[30],我們可以給出瞬時(shí)系綜平均功率P(t)和平均熱流J(t)的定義(正方向都規(guī)定為流入系統(tǒng)的方向):

其中F ≡?×A為參數(shù)空間的幾何曲率,積分的范圍為驅(qū)動(dòng)路徑所圍繞的參數(shù)范圍Ω,dS為面元向量.可以看出,Wgeo的形式與孤立量子系統(tǒng)中的Berry 相位的形式[31,32]具有很強(qiáng)的類(lèi)比性,因此被稱(chēng)為幾何相(曲率)貢獻(xiàn)的非平衡功.幾何相(曲率)貢獻(xiàn)的熱也同理可得,并滿足Qgeo=-Wgeo.這里作為示例,僅推導(dǎo)了平均意義下功的形式,任意非平衡漲落流的幾何相描述和它與Berry 相位進(jìn)一步的類(lèi)比將在下一節(jié)中以生成函數(shù)的形式給出.
上面所推導(dǎo)的結(jié)果為慢驅(qū)動(dòng)下的熱-功轉(zhuǎn)換.若將驅(qū)動(dòng)方向反向,則這部分的貢獻(xiàn)也會(huì)反向,因此它代表了可逆的部分.若要研究熱-功轉(zhuǎn)換中的不可逆性、耗散以及效率,則需要引入量子隨機(jī)熵[29,33]和熱力學(xué)距離[23,24]的概念.下面仍將在此示例系統(tǒng)中進(jìn)行推導(dǎo).在雙參數(shù)驅(qū)動(dòng)下,

研究工作[33]已經(jīng)將經(jīng)典系統(tǒng)中隨機(jī)熵的定義[34]推廣到了受驅(qū)動(dòng)量子系統(tǒng)中.受驅(qū)動(dòng)的過(guò)程中,整體的熵增可以拆分為系統(tǒng)和熱庫(kù)的熵增兩部分.此時(shí),平均熵產(chǎn)生速率可以寫(xiě)成[33]:
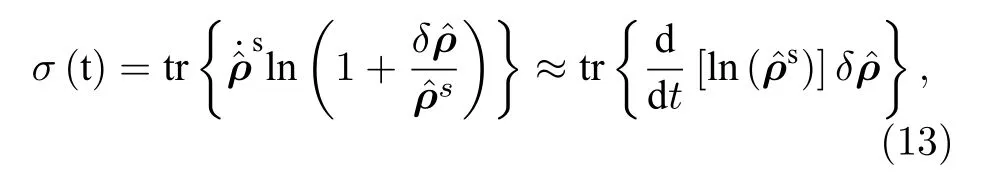
在劉維爾表象下,上面熵增速率可以寫(xiě)作:

由此定義的度規(guī)gμν ≡(Rμν+Rνμ)/2是Rμν的對(duì)稱(chēng)部分,刻畫(huà)了慢驅(qū)動(dòng)過(guò)程中的瞬時(shí)平均熵增速率.從這里容易看出,Rμν的反對(duì)稱(chēng)部分對(duì)于熵的產(chǎn)生沒(méi)有貢獻(xiàn).圖1(b)中,用曲線坐標(biāo)系定性地表現(xiàn)了gμν描述的參數(shù)點(diǎn)間的局域熱力學(xué)距離.可以看到,若將參數(shù)驅(qū)動(dòng)的方向反向,幾何相(曲率)的貢獻(xiàn)也會(huì)反向,但熱力學(xué)距離以及熵產(chǎn)生的符號(hào)不會(huì)改變.因此,熱力學(xué)距離在物理上描述了驅(qū)動(dòng)帶來(lái)的不可逆性,而幾何相(曲率)貢獻(xiàn)則代表了可逆的能量轉(zhuǎn)換.
根據(jù)Cauchy-Schwarz 不等式,可以一般性地給出對(duì)于熵產(chǎn)生的限制,此極限由熱力學(xué)給出:

與幾何相(曲率)貢獻(xiàn)的平均流類(lèi)似,熱力學(xué)幾何也是一個(gè)普遍框架.這里僅舉例說(shuō)明它在最簡(jiǎn)單系統(tǒng)中的應(yīng)用.若采取不同的定義,可以研究驅(qū)動(dòng)系統(tǒng)中功率-效率的權(quán)衡關(guān)系[25],多個(gè)熱庫(kù)的系統(tǒng)中的權(quán)衡關(guān)系[20],以及受驅(qū)動(dòng)量子熱機(jī)的多目標(biāo)優(yōu)化[26]等等.但這些都具有相類(lèi)似的理解方式.這正說(shuō)明了幾何方法在受驅(qū)動(dòng)量子系統(tǒng)中,研究能量轉(zhuǎn)換時(shí)所發(fā)揮的普適框架性作用.后文將進(jìn)一步介紹.
3 幾何相:可逆熱泵浦和慢驅(qū)動(dòng)熱機(jī)
類(lèi)似于第2節(jié)的分析,在慢驅(qū)動(dòng)情況,時(shí)間驅(qū)動(dòng)帶來(lái)的累積熱流和功可以寫(xiě)成一個(gè)不依賴(lài)驅(qū)動(dòng)頻率的幾何性表達(dá)式.但是上面的分析沒(méi)有考慮多個(gè)熱庫(kù)的情況,也沒(méi)有包含累積流的漲落的性質(zhì).本節(jié)將在生成函數(shù)的框架下對(duì)這兩個(gè)問(wèn)題進(jìn)行討論.
非熱力學(xué)的幾何泵浦的研究可以追溯到Thouless[32]關(guān)于零溫孤立且受周期性參數(shù)驅(qū)動(dòng)的電子系統(tǒng)的研究,他發(fā)現(xiàn)一個(gè)周期內(nèi)泵浦的電荷量是量子化的,且它受到拓?fù)浔Wo(hù),具有很強(qiáng)的魯棒性.此時(shí),量子化的泵浦量可以寫(xiě)成Berry 曲率[31]在驅(qū)動(dòng)參數(shù)和一維布里淵區(qū)所組成的二維面上的積分.這項(xiàng)開(kāi)創(chuàng)性工作開(kāi)啟了周期性驅(qū)動(dòng)系統(tǒng)中輸運(yùn)性質(zhì)的研究.后續(xù),人們發(fā)現(xiàn),在開(kāi)放量子系統(tǒng)中也可以實(shí)現(xiàn)類(lèi)似的現(xiàn)象.特別地,即便不存在靜態(tài)偏壓,也可以周期性驅(qū)動(dòng)產(chǎn)生定向電流.此電流可以用散射矩陣表達(dá)出來(lái)[35].此外,相互作用量子點(diǎn)系統(tǒng)具有在實(shí)驗(yàn)中展現(xiàn)出此類(lèi)現(xiàn)象的潛力[36].后續(xù)Sinitsyn和Nemenman[37]的研究說(shuō)明,幾何泵浦的現(xiàn)象不局限于電子系統(tǒng),而具有廣泛的應(yīng)用.他們使用生成函數(shù)的方法,給出了隨機(jī)泵浦系統(tǒng)中,包含泵浦流各階漲落信息的幾何相貢獻(xiàn).
然而,上面的研究只探討了粒子流的定向輸運(yùn),而沒(méi)有研究周期驅(qū)動(dòng)過(guò)程中熱流等能流的輸運(yùn)情況.基于隨機(jī)熱力學(xué)的研究方法[38],Ren 等[15]提出了量子分子結(jié)的聲子熱輸運(yùn)中,驅(qū)動(dòng)熱庫(kù)溫度等參數(shù)產(chǎn)生幾何相熱流的熱泵.隨后,幾何相熱流也在經(jīng)典布朗系統(tǒng)[17],自旋-玻色系統(tǒng)[18,39],量子光力系統(tǒng)[16]等大量系統(tǒng)中得到了廣泛研究.特別地,在自旋-玻色系統(tǒng)中,研究人員發(fā)展運(yùn)用了極化子變換的方法[40],系統(tǒng)性探討了系統(tǒng)-熱庫(kù)耦合從弱到強(qiáng)的變化對(duì)于幾何相熱流的影響[18,41].
為了幫助對(duì)于這一大類(lèi)工作的理解,下面大致梳理了幾何相熱泵浦[42]的基本思想和理論框架.
根據(jù)兩點(diǎn)測(cè)量的方法可以定義從熱庫(kù)流入系統(tǒng)的累積隨機(jī)熱流.若在時(shí)刻 0和t分別測(cè)出熱庫(kù)的能量為m0和mt,則流入系統(tǒng)的熱流為Q=m0-mt.將此事件的聯(lián)合概率密度記作P(mt,t;m0,0),它表示熱庫(kù)在 0 時(shí)刻總能量為m0,且在經(jīng)過(guò)酉演化后第二次測(cè)量時(shí)熱庫(kù)具有總能量mt的聯(lián)合概率.在這個(gè)過(guò)程中流入系統(tǒng)的熱流的生成函數(shù)為[2,38]
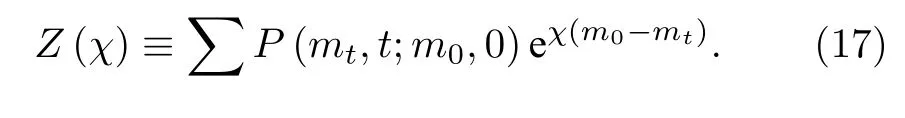
χ是計(jì)數(shù)參數(shù).對(duì)應(yīng)地,熱流的累積量(cumulant)生成函數(shù)為
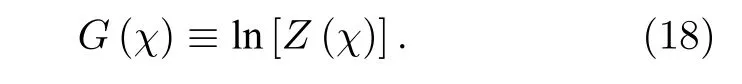
通過(guò)對(duì)它求導(dǎo),可以給出熱流的各階累積量:
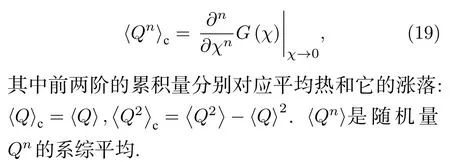
若假設(shè)系統(tǒng)-熱庫(kù)的耦合相對(duì)于系統(tǒng)和熱庫(kù)各自的能量來(lái)說(shuō)為弱耦合,則可以用一個(gè)帶有計(jì)數(shù)參數(shù)χ的量子主方程來(lái)同時(shí)描述系統(tǒng)密度矩陣和流的生成函數(shù)的演化[15,39]:
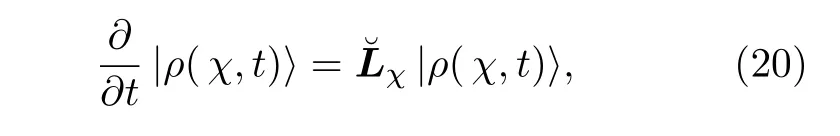
其中下標(biāo)表示對(duì)于計(jì)數(shù)參數(shù)χ的依賴(lài).若計(jì)數(shù)參數(shù)χ=0,則此方程對(duì)應(yīng)的是只描述系統(tǒng)密度矩陣演化的主方程.可以根據(jù)得到其穩(wěn)態(tài)下的左右本征矢:

其中 dSμν為特定方向的面元,反對(duì)稱(chēng)的幾何曲率Fμν ≡?μAν -?νAμ為參數(shù)空間的內(nèi)稟量,不依賴(lài)于規(guī)范的選取.如果把驅(qū)動(dòng)路徑反向,熱的幾何相效應(yīng)也反向.因此,在只有純的幾何相效應(yīng)(動(dòng)力學(xué)相效應(yīng)為零)的情況下,系統(tǒng)為可逆熱泵浦和熱機(jī).
近年來(lái),大量關(guān)于受驅(qū)動(dòng)非平衡量子系統(tǒng)中熱流泵浦的研究基本都基于以上描述的理論框架.如圖2(a)所示,最初關(guān)于幾何熱泵的研究是關(guān)于一個(gè)量子分子結(jié)的聲子熱泵[15].通過(guò)動(dòng)態(tài)驅(qū)動(dòng)分子結(jié)兩端熱庫(kù)的溫度,可以產(chǎn)生一個(gè)累積的定向熱流.這個(gè)熱流的一部分累積量生成函數(shù)可以和Berry相位進(jìn)行對(duì)應(yīng),由一個(gè)純幾何量給出,即幾何曲率(如圖2(b))在驅(qū)動(dòng)包裹的參數(shù)空間區(qū)域內(nèi)的積分.幾何相熱流的存在,使得靜態(tài)條件下普適成立的漲落定理被打破.后續(xù)關(guān)于此情況下新的形式的漲落定理被推導(dǎo)得出,此特殊的漲落定理需要考慮幾何相熱流的貢獻(xiàn)[43].
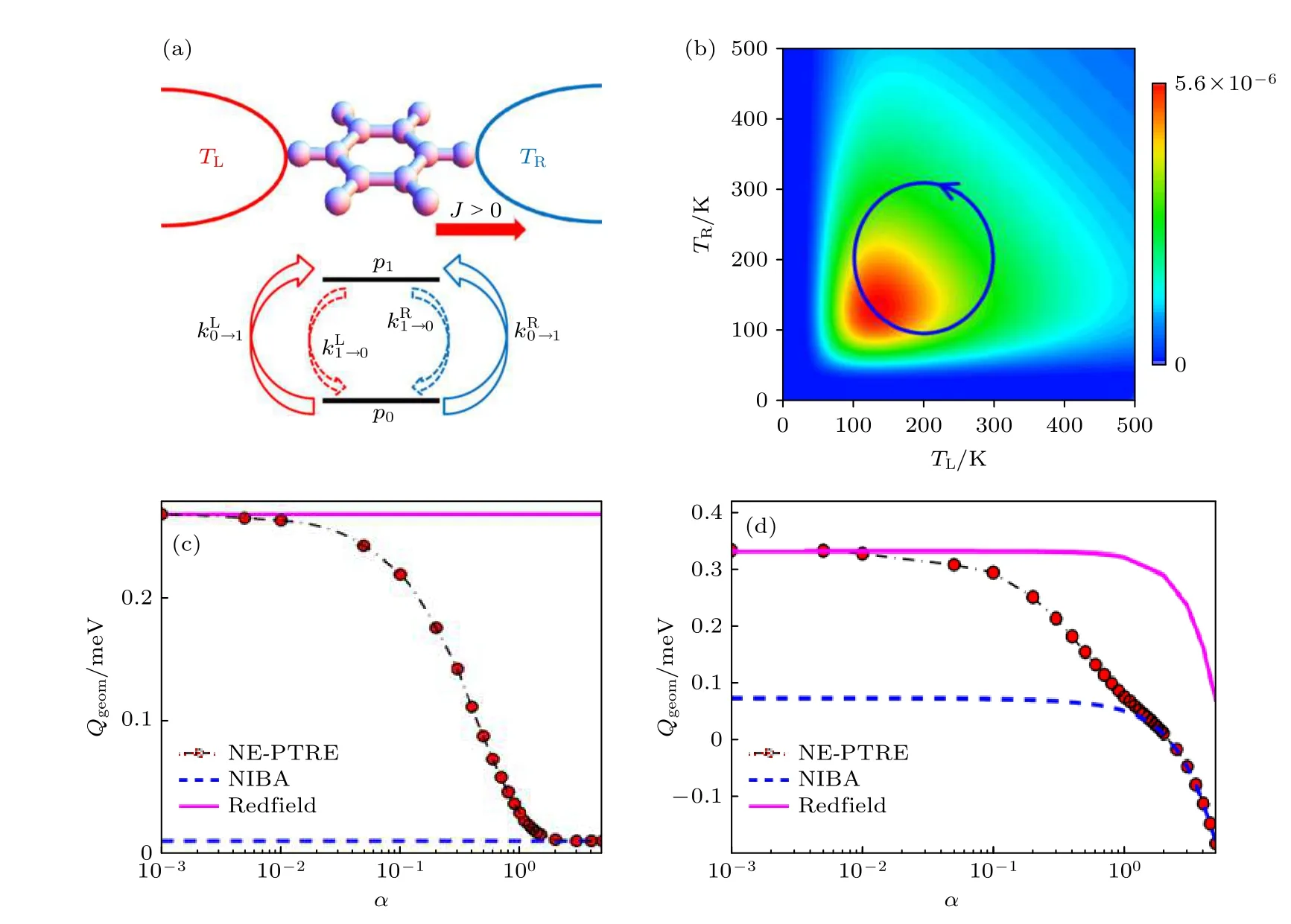
圖2 幾何相熱泵浦 (a) 最初研究的量子分子結(jié)系統(tǒng),工作介質(zhì)由一個(gè)兩能級(jí)系統(tǒng)描述,p和k 分別為各個(gè)占據(jù)數(shù)和躍遷速率[15];(b) 驅(qū)動(dòng)兩端溫度產(chǎn)生的熱泵浦現(xiàn)象,圖中用顏色表示了幾何曲率的大小.幾何泵浦的熱量為驅(qū)動(dòng)回路包裹的范圍內(nèi)的幾何曲率積分[15].(c),(d)自旋-玻色系統(tǒng)中幾何相熱流與系統(tǒng)-熱庫(kù)耦合強(qiáng)度 α 的關(guān)系[18].(c)為無(wú)Zeeman 劈裂能的情形;(d)為有Zeeman 劈裂能的情形[18].(a),(b)改編自文獻(xiàn)[15];(c),(d)改編自文獻(xiàn)[18]Fig.2.The geometric heat pump effect.(a) The originally studied quantum molecular junction system.The working medium is described by a quantum two-level system,with pand k denoting different populations and transition rates[15].(b) The geometric curvature in the two-temperature parameter space.The color denotes the magnitude of the geometric curvature.The pumped heat is the integral of geometric curvature over the encircled area[15].(c),(d) The geometrically pumped heat versus the coupling strength between the middle system and reservoirs in a quantum spin-boson system[18].(c) is for the setup with no Zeeman splitting while the splitting is present in (d) [18].(a),(b) are adapted from [15],while (c),(d) are adapted from [18].
隨后,除了經(jīng)典布朗系統(tǒng)中的幾何熱泵浦現(xiàn)象外[17],更多量子系統(tǒng)中的幾何相熱泵浦也得到了大量關(guān)注.在自旋-玻色系統(tǒng)中,系統(tǒng)-熱庫(kù)耦合強(qiáng)度對(duì)于幾何相熱流的調(diào)控得到了研究[18].如圖2(c)和圖2(d)所示,在沒(méi)有Zeeman 劈裂能時(shí),幾何相熱流隨著耦合強(qiáng)度的增加而單調(diào)衰減;而當(dāng)有Zeeman 劈裂時(shí),幾何相熱流先隨耦合強(qiáng)度的增加而減小,后經(jīng)過(guò)反向后,絕對(duì)值又繼續(xù)增大.這說(shuō)明幾何相熱流可以方便地在量子系統(tǒng)中被控制.另外,在量子光力系統(tǒng)中,可以調(diào)控的參數(shù)更多,例如失諧,光驅(qū)動(dòng)的壓縮性質(zhì)等等,由此在光力系統(tǒng)中引入周期驅(qū)動(dòng),也可以實(shí)現(xiàn)熱流的幾何泵浦和非互易傳輸[16].
為了使幾何相泵浦不再局限于慢驅(qū)動(dòng)附近,研究人員借鑒了量子控制和非絕熱控制[44]的概念,在設(shè)計(jì)驅(qū)動(dòng)方案時(shí),研究了對(duì)幾何相泵浦的非絕熱控制[45,46].通過(guò)引入一個(gè)附加的驅(qū)動(dòng)項(xiàng),可以把幾何相的描述方法拓寬到相對(duì)高頻的參數(shù)條件,從而極大地增大了幾何泵浦的功率,在單位時(shí)間內(nèi)可以將更多熱量/粒子泵浦到特定熱庫(kù)中去.
除了實(shí)現(xiàn)定向泵浦,幾何相的概念也可以被應(yīng)用在研究慢驅(qū)動(dòng)下熱機(jī)工作分析.Giri和Goswami[19]分析了三端口熱機(jī)中幾何相的貢獻(xiàn),通過(guò)驅(qū)動(dòng)高溫和低溫端熱庫(kù)的溫度,可以向光學(xué)腔內(nèi)單一模式中泵浦光子.特別地,他們通過(guò)引入兩個(gè)接近簡(jiǎn)并的能級(jí),探究了量子相干性對(duì)于泵浦的影響,相對(duì)于動(dòng)力學(xué)相對(duì)應(yīng)的功的行為,兩個(gè)近簡(jiǎn)并能級(jí)間的相位差可以更明顯地調(diào)制幾何相部分的功.幾何相的存在,使得穩(wěn)態(tài)熱機(jī)在取得最大功率時(shí)效率的普適極限被打破.
在上面這些面向?qū)嶋H應(yīng)用的研究外,生成函數(shù)的幾何相也在關(guān)于非平衡統(tǒng)計(jì)物理的基礎(chǔ)理論中發(fā)揮了作用.早期關(guān)于穩(wěn)態(tài)統(tǒng)計(jì)物理的研究希望能找到一個(gè)類(lèi)似于平衡態(tài)Claussius 不等式的關(guān)系,由此可以給出系統(tǒng)在不同穩(wěn)態(tài)間切換時(shí)所要滿足的限制.Hatano和Sasa[47]指出,可以將熵產(chǎn)生拆分為瞬時(shí)穩(wěn)態(tài)熵(housekeeping entropy)和額外熵(excess entropy),且根據(jù)額外熵滿足的漲落定理(Hatano-Sasa 等式)可以限制不同穩(wěn)態(tài)間切換的過(guò)程.近期,Sagawa 等[22]的工作表明,幾何相正好對(duì)應(yīng)了額外熵的累積量生成函數(shù),而同時(shí)動(dòng)力學(xué)相則對(duì)應(yīng)了瞬時(shí)穩(wěn)態(tài)熵的統(tǒng)計(jì)性質(zhì).這樣的工作說(shuō)明,幾何相對(duì)應(yīng)的熱力學(xué)過(guò)程不僅具有實(shí)際應(yīng)用的價(jià)值,也對(duì)基本非平衡理論的研究具有指導(dǎo)作用.
4 熱力學(xué)距離:熱機(jī)中的不可逆性
第3節(jié)中描述的幾何相貢獻(xiàn)沒(méi)有分析驅(qū)動(dòng)過(guò)程中帶來(lái)的不可逆性和由此帶來(lái)的熱力學(xué)效率的減小.本節(jié)將運(yùn)用熱力學(xué)距離的概念對(duì)此進(jìn)行討論.熱力學(xué)距離最初源于宏觀平衡熱力學(xué)的研究,它基于熱力學(xué)勢(shì)函數(shù)(內(nèi)能,熵等)在參數(shù)空間中的二階導(dǎo)數(shù),且其發(fā)散性代表了相變的發(fā)生[48,49].近年來(lái),此概念被用來(lái)描述單一熱庫(kù)接觸的微納系統(tǒng)的熱力學(xué)和統(tǒng)計(jì)物理性質(zhì),與前面宏觀系統(tǒng)的情況不同,此時(shí)的熱力學(xué)距離基于隨機(jī)的香農(nóng)熵(S=-lnp)來(lái)定義[23].此時(shí)的熱力學(xué)度規(guī)與信息幾何中的Fisher 信息矩陣直接相關(guān),即:當(dāng)把Fisher信息定義中的概率分布選取為Gibbs 分布,則可以得到對(duì)應(yīng)的熱力學(xué)度規(guī).根據(jù)此度規(guī)計(jì)算的兩點(diǎn)間的熱力學(xué)距離確定了這兩點(diǎn)間態(tài)轉(zhuǎn)換的最小耗散,這與信息幾何中Cramer-Rao 界限具有很強(qiáng)的類(lèi)比性.此時(shí)的熱力學(xué)距離是一個(gè)實(shí)驗(yàn)可直接測(cè)量的量[50],它可以幫助人們?cè)O(shè)計(jì)進(jìn)行微納系統(tǒng)態(tài)轉(zhuǎn)換時(shí)最優(yōu)(耗散最小)的路徑方案,此方案對(duì)應(yīng)著參數(shù)空間中由熱力學(xué)度規(guī)確定的測(cè)地線[24,51].
上面一系列重要的研究?jī)H僅關(guān)注了受驅(qū)動(dòng)系統(tǒng)的耗散性質(zhì),而沒(méi)有研究受到周期驅(qū)動(dòng)的微納系統(tǒng)中涉及的熱機(jī)功能以及其能量轉(zhuǎn)換效率.近期,Brandner和Saito[25]的研究工作討論了這個(gè)問(wèn)題.類(lèi)似于本文第2節(jié)中的討論,他們用幾何聯(lián)絡(luò)來(lái)描述慢驅(qū)動(dòng)產(chǎn)生的功輸出,用熱力學(xué)度規(guī)來(lái)描述驅(qū)動(dòng)帶來(lái)的耗散.如圖3(a)中給出的,熱力學(xué)幾何限定了有限時(shí)間熱機(jī)工作時(shí)的效率-功率權(quán)衡關(guān)系.圖中的灰色區(qū)域?yàn)闊崃W(xué)幾何給出的不等式所禁止的,即在一定范圍內(nèi)若要獲得更大的效率就要犧牲一部分功率.而圖3(a)中黑線為以勻速驅(qū)動(dòng)的結(jié)果,而橙線則代表了經(jīng)過(guò)優(yōu)化的熱機(jī)表現(xiàn),具體的優(yōu)化方式將在下一節(jié)中進(jìn)行描述.另一方面,與先前的結(jié)果[6]不同,在此研究的具體模型中,無(wú)論驅(qū)動(dòng)的幅度如何,量子相干性(由驅(qū)動(dòng)引起)都只會(huì)損害熱機(jī)的工作性能.
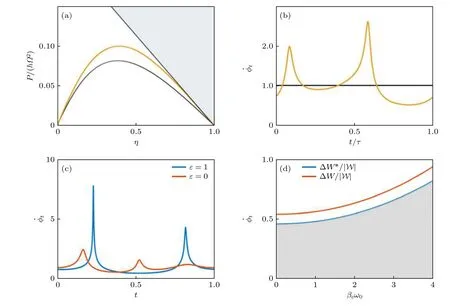
圖3 通過(guò)熱力學(xué)距離對(duì)慢驅(qū)動(dòng)熱機(jī)的限制和優(yōu)化 (a) 周期驅(qū)動(dòng)量子熱機(jī)中的功率與效率權(quán)衡.灰色區(qū)域是根據(jù)熱力學(xué)幾何得出的不可能區(qū)域,黑色線對(duì)應(yīng)等速率驅(qū)動(dòng)方式,而橙色線對(duì)應(yīng)經(jīng)過(guò)優(yōu)化的驅(qū)動(dòng)方式(驅(qū)動(dòng)速度隨時(shí)間變化),這兩種驅(qū)動(dòng)方式中驅(qū)動(dòng)速度的具體形式由圖(b)給出[25].(c),(d) 對(duì)于驅(qū)動(dòng)量子熱機(jī)(一個(gè)諧振子)的多目標(biāo)優(yōu)化[26] (c)不同的優(yōu)化后的驅(qū)動(dòng)速度;(d) 功的相對(duì)漲落與諧振子頻率的關(guān)系,此時(shí)為效率-功漲落的多目標(biāo)優(yōu)化.紅線為勻速率的驅(qū)動(dòng),而藍(lán)線對(duì)應(yīng)優(yōu)化后的驅(qū)動(dòng),灰色區(qū)域?yàn)橛蔁崃W(xué)幾何給出的不可能區(qū)域[26].(a),(b)改編自文獻(xiàn)[25];(c),(d)改編自文獻(xiàn)[26]Fig.3.The constraint on and optimization of slowly driven quantum heat engine using the thermodynamics distance method:(a) The efficiency-power tradeoff in driven quantum heat engine.The gray area is ruled out by the thermodynamic geometry,with the black and orange line corresponding to the constant-speed driving and optimized driving protocols (driving speed is time dependent) respectively.The driving speed in these two protocols is illustrated in Figure (b)[25].(c),(d) A multiple target optimization of a driven heat engine composed of a harmonic oscillator:(c) the driving speed of the optimization result with different targets[26];(d) the relative work fluctuation versus the oscillator’s frequency (system’s parameter) with a multiple target optimization.The red line is for the constant speed driving while the blue one is for the optimized protocol.The gray area is prohibited by the thermodynamic geometry[26].(a),(b) are adapted from Ref.[25],while (c),(d) are adapted from Ref.[26].
盡管上面的理論適用于大量受到慢驅(qū)動(dòng)的經(jīng)典/量子系統(tǒng),但卻要求系統(tǒng)僅與一個(gè)熱庫(kù)相連.隨后,Hino和Hayakawa[20]將此框架推廣到了同時(shí)與多個(gè)熱庫(kù)相接的系統(tǒng)中去,并以此分析了非平衡自旋-玻色模型中的效率和功率.此時(shí),熱力學(xué)距離的定義不再像單一熱庫(kù)時(shí)那樣依據(jù)Gibbs 分布,而是運(yùn)用了Hatano-Sasa 等式中的額外熵.此理論可以用在無(wú)驅(qū)動(dòng)時(shí)處于穩(wěn)態(tài)的熱機(jī)中,但由于穩(wěn)態(tài)分布在較復(fù)雜系統(tǒng)時(shí)難以直接得到,因此,提出另外的計(jì)算熱力學(xué)距離的方法顯得尤為重要.
在線性響應(yīng)區(qū)域,可以把驅(qū)動(dòng)和靜態(tài)偏置同等地當(dāng)作一個(gè)平衡態(tài)附近的微小擾動(dòng)來(lái)處理.此時(shí),熱力學(xué)距離可以直接表示為一個(gè)平衡態(tài)的關(guān)聯(lián)函數(shù),但此方法僅局限于驅(qū)動(dòng)幅度和偏置幅度都較小的線性響應(yīng)區(qū)域[52,53].根據(jù)平衡態(tài)關(guān)聯(lián)函數(shù)可計(jì)算出熱力學(xué)張量,它的對(duì)稱(chēng)部分為熱力學(xué)度規(guī),反對(duì)稱(chēng)部分為幾何曲率,這就把本文第2節(jié)中介紹的看似分離的兩部分內(nèi)容聯(lián)系了起來(lái)[54].特別地,基于線性響應(yīng)計(jì)算熱力學(xué)距離的方法可以處理受驅(qū)動(dòng)導(dǎo)體中的相干輸運(yùn),給出對(duì)于輸運(yùn)系數(shù)的熱力學(xué)限制[55].這將有助于進(jìn)一步考察更復(fù)雜量子系統(tǒng)中的輸運(yùn)現(xiàn)象.
5 基于幾何方法的能量轉(zhuǎn)換優(yōu)化與權(quán)衡關(guān)系

因此,?(t) 需要滿足的方程為
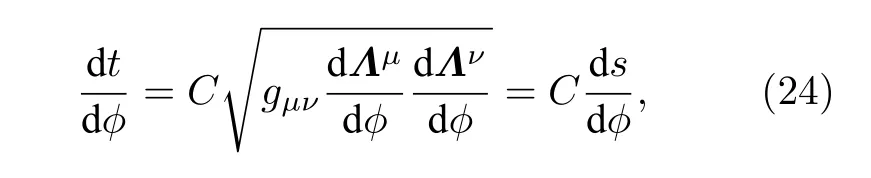
C為一個(gè)待定的常數(shù),s為沿驅(qū)動(dòng)路徑累積的熱力學(xué)距離.這時(shí)在一個(gè)參數(shù)點(diǎn)附近停留的時(shí)間正比于此處驅(qū)動(dòng)路徑的局域熱力學(xué)距離.從而求出最優(yōu)的驅(qū)動(dòng)函數(shù)應(yīng)當(dāng)為

其中給定驅(qū)動(dòng)路徑后,?(t) 確定了參數(shù)空間中的具體位置,而t就表示從初始位置驅(qū)動(dòng)到此處所要花費(fèi)的時(shí)間.按此方式選擇的驅(qū)動(dòng),可以使得熱力學(xué)系統(tǒng)的整體耗散最小.由于經(jīng)歷完整周期的驅(qū)動(dòng)后,(25)式變?yōu)棣觩=CL.因此常數(shù)C=τp/L.可以看出,當(dāng)驅(qū)動(dòng)最優(yōu)時(shí),驅(qū)動(dòng)路徑Λ(t) 以熱力學(xué)距離為參數(shù).此時(shí),經(jīng)過(guò)相同長(zhǎng)度的時(shí)間,參數(shù)空間內(nèi)應(yīng)走過(guò)熱力學(xué)度規(guī)給出的相同的距離.
在對(duì)于單一目標(biāo)(如效率)進(jìn)行優(yōu)化時(shí),可以通過(guò)計(jì)算參數(shù)空間中熱力學(xué)度規(guī),然后確定出最優(yōu)的驅(qū)動(dòng)方式[25].不同于一般性的直接優(yōu)化方式[14],此優(yōu)化過(guò)程是不需要大量數(shù)值性優(yōu)化過(guò)程的.另外,如圖3(c)和圖3(d)中的例子,若優(yōu)化的目標(biāo)為多目標(biāo)優(yōu)化,則可以根據(jù)?這樣的參數(shù),調(diào)節(jié)優(yōu)化時(shí)的權(quán)重,決定一定程度上犧牲哪一個(gè)目標(biāo)來(lái)?yè)Q取另一個(gè)目標(biāo)的優(yōu)化.根據(jù)不同?計(jì)算出的熱機(jī)表現(xiàn),就確定了它在多個(gè)衡量標(biāo)準(zhǔn)時(shí)的Pareto 前沿[26].
6 總結(jié)
在近些年的研究中,來(lái)源于幾何的概念—幾何相和熱力學(xué)距離—給受驅(qū)動(dòng)微納量子系統(tǒng)中熱泵浦和熱-功轉(zhuǎn)換現(xiàn)象的研究提供了一種普適的方法和理解的角度.一般地,一個(gè)隨機(jī)流的累積量產(chǎn)生函數(shù)中包含了驅(qū)動(dòng)帶來(lái)的幾何相貢獻(xiàn).這部分貢獻(xiàn)是可逆的,平均流的方向會(huì)因?yàn)轵?qū)動(dòng)方向的轉(zhuǎn)變而翻轉(zhuǎn).它可以用一個(gè)反對(duì)稱(chēng)的張量(幾何曲率)來(lái)描述.在慢驅(qū)動(dòng)極限下,驅(qū)動(dòng)產(chǎn)生的定向熱流、功提取、中間系統(tǒng)的額外熵等物理量都可以用一個(gè)類(lèi)似于Berry 相位(曲率)的幾何相(曲率)來(lái)表示.在此范圍內(nèi),幾何相熱流是一個(gè)重要的可測(cè)量物理量,它可以幫助人們實(shí)現(xiàn)在無(wú)靜態(tài)偏置時(shí)的便捷的熱流調(diào)控.一系列理論研究已經(jīng)涵蓋了量子分子結(jié)、自旋-玻色模型和量子光力系統(tǒng)等實(shí)際系統(tǒng)中各系統(tǒng)參數(shù)對(duì)于幾何相熱流的調(diào)控作用.
另一方面,源于熱力學(xué)距離的幾何度規(guī)則是一個(gè)對(duì)稱(chēng)張量,它不會(huì)隨著驅(qū)動(dòng)反向而反向.在具體的應(yīng)用中,它可以被用來(lái)研究周期驅(qū)動(dòng)量子熱機(jī)中對(duì)于功率、效率、漲落的熱力學(xué)限制,也可以在慢驅(qū)動(dòng)條件下直接給出最優(yōu)的驅(qū)動(dòng)方式.
上面這兩者,是非平衡量子系統(tǒng)的參數(shù)空間里內(nèi)稟幾何性質(zhì)的不同體現(xiàn).它可以幫助人們用統(tǒng)一的方式去研究大多數(shù)受驅(qū)動(dòng)量子系統(tǒng)中的能流和能量轉(zhuǎn)換過(guò)程.未來(lái),它將指導(dǎo)人們?cè)O(shè)計(jì)出更具實(shí)用價(jià)值的量子熱機(jī)[56,57],量子熱泵和量子制冷機(jī)等功能性量子熱器件.本文的討論局限在弱耦合系統(tǒng),若未來(lái)能正確考慮系統(tǒng)-熱庫(kù)間一般耦合帶來(lái)的非馬爾可夫效應(yīng),則可以拓寬非平衡系統(tǒng)中幾何性質(zhì)研究的應(yīng)用場(chǎng)景.

