二自由度電磁軸承轉子系統的動力學分析
陳淑婕 李欣業 張華彪 張利娟


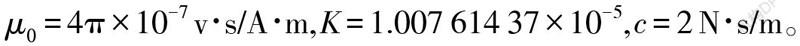
摘要 根據麥克斯韋電場理論得到的電磁力模型并結合PD控制理論,在差動激磁方式下建立了二自由度電磁軸承轉子系統的動力學方程。基于多尺度法對泰勒展開后的方程進行攝動分析,求得了關于系統振幅和相位的平均方程。利用同倫延拓法對平均方程進行求解,得到了系統的幅頻特性曲線,發現幅頻特性曲線表現出明顯的滯后現象,在升速和降速通過共振區域時都會發生跳躍,利用數值仿真對解析計算的正確性進行了驗證。分析了電流及控制參數對幅頻特性曲線的影響,研究表明共振區域的最大振幅及其對應轉速隨著電流的增大而增大,隨比例系數的增大而減小。
關 鍵 詞 電磁軸承轉子系統;非線性動力學;PD控制;多尺度法;數值仿真
中圖分類號 O322? ? ?文獻標志碼 A
Abstract According to the electromagnetic force model obtained by Maxwell's electric field theory and PD control theory, the dynamic equation of the two-degree-of-freedom electromagnetic bearing rotor system is established under differential excitation mode. The perturbation analysis of Taylor's expanded equations is based on the method of multiple scales, and the average equations for the amplitude and phase of the system are obtained. Using the homotopy continuation method to solve the average equation, the amplitude-frequency characteristic curve of the system is given. It is found that the amplitude-frequency characteristic curve shows obvious hysteresis, and jumps occur when the speed is increased and the speed is reduced. The simulation verified the correctness of the analytical calculation. The influence of current and control parameters on the amplitude-frequency characteristic curve is analyzed. The results show that the maximum amplitude of the resonant region and its corresponding rotational speed increase with the increase of current, and decrease with the increase of the proportional coefficient.
Key words active magnetic bearing rotor system; nonlinear dynamics; PD control; the method of multiple scales; numerical simulation
0 引言
電磁軸承(Active Magnetic Bearing,AMB)具有無接觸、無潤滑、允許轉子高速旋轉、功耗低、維護成本低且壽命長[1-2]等優點,從而得到了越來越廣泛的應用。但是由于電磁軸承轉子系統固有的非線性,使其表現出非常復雜的動力學特性。所以電磁軸承轉子系統的非線性動力學及其控制問題一直備受研究者的關注。
Schweitzer 等[1]系統地介紹了主動磁軸承的基本原理、總體結構以及各組成部分的設計方法,為后面的研究奠定了理論基礎;魏金強[3]以五自由度磁懸浮軸承為研究對象,設計了系統的主要電磁參數,并對傳統算法和模糊PID控制進行了研究,最終實現了模糊PID控制算法,滿足了系統的控制要求,實現了系統的精確控制;Ji等[4]研究了主動磁電磁軸承轉子系統的非線性響應問題,利用多尺度方法對其進行了攝動分析,結果表明,穩態解通過鞍結點分岔或Hopf分岔失去穩定性。李澤輝等[5]以自行設計的磁懸浮儲能飛輪測試樣機以徑向磁懸浮軸承為例,應用ANSYS有限元分析軟件對徑向磁懸浮軸承磁路進行仿真與計算;安華貞等[6]研究了電磁軸承的非線性振動,利用牛頓定律對電磁軸承轉子系統進行了動力學建模,由于非線性項的影響,系統出現了正規、橢圓、準周期等運動類型;文獻[7]基于四極對模型和PID控制研究了徑向電磁軸承的可控性問題;王媛[8]研究了電磁軸承轉子系統的非線性動力學特性,建立了轉子系統的運動方程并進行了數值仿真,結果得到了轉子中心軌跡圖、相應的時間歷程圖、分岔圖及Poincaré映射圖。展示了電磁軸承轉子系統的周期解、準周期解等非線性動力學行為;虞烈等[1]系統介紹了軸承轉子系統動力學的基本理論及其在工程中的應用,內容涉及了單跨單質量轉子軸承系統、多跨多質量轉子軸承系統、多平行軸系統和電磁軸承轉子系統等;劉熙娟[9]針對一類電磁軸承-剛性轉子系統,研究了它在某些參數區域中出現的Hopf分岔、全局分岔等動力學現象。對轉子系統在局部處的動力學特征進行了定性、定量的研究。通過中心流形定理,對四維高階系統進行降維操作得到了二維降階系統。利用范式理論對該降維系統進行分析,發現該軸承-轉子系統在局部處發生了超臨界Hopf分岔。對系統進行數值模擬得到分岔圖,驗證了理論分析的正確性。張海燕[10]研究了電磁軸承轉子系統的非線性動力學,發現了電磁軸承轉子系統在某些參數區域內出現全局分叉和混沌運動情況。季進臣等[11]對高速不平衡剛性轉子在應急情況下跌落在保持軸承內的非線性動力學進行了研究,數值分析了轉子的瞬態響應,給出了跌落過程中轉子在保持軸承中的軌跡、滑動渦動階段的速度和功率損耗。
本文利用非線性動力學理論對電磁軸承轉子系統進行了分析,運用PD控制理論對電磁軸承轉子系統的非線性振動進行控制研究,并利用多尺度法對無量綱化后的運動微分方程進行求解,得到平均方程,再利用同倫延拓法對平均方程進行穩定性分析,最終得到解的幅頻特性曲線。將利用MATLAB對無量綱化后的運動微分方程求解得到的幅頻特性曲線與利用多尺度法及同倫延拓法求解得到的幅頻特性曲線作對比,發現數值仿真的結果與理論分析的結果相吻合,證明了理論推導的正確性。同時分析了電流和控制參數對幅頻特性曲線的影響。以及共振區域最大振幅和最大振幅對應的轉速與電流和控制參數的關系。
1 兩自由度電磁軸承轉子系統的動力學模型
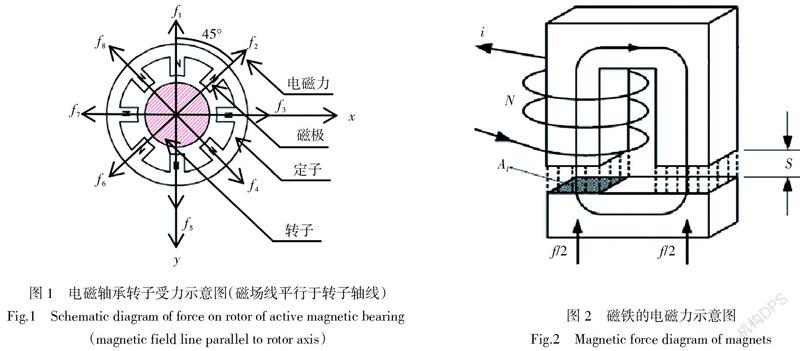
對如圖1所示結構的電磁軸承,定子端面橫截面極性相同,稱為同極磁極。這種結構的優點是磁極周圍的磁場變化較小,從而使渦流的變化減小因而無需使用疊片,這便使得這種軸承可應用于由于某些原因不能使用疊片的場合。圖2為磁鐵的電磁力示意圖。
1.1 電磁力模型
電磁軸承轉子系統是一個集機、電、磁一體化的綜合系統,電磁力的計算涉及磁場和磁路。磁鐵的吸引力產生在具有不同導磁率的界面上,這些力的計算以磁場能量為基礎。在閉合系統中,力f可由虛位移原理導出:
在建立模型之前,先將轉子作為集中質量處理、忽略繞組漏磁、忽略鐵芯和轉子中的磁阻即認為磁勢均勻降落在氣隙上并且忽略磁性材料的磁滯和渦流。
根據電磁理論,通過每一個磁極產生的電磁力[fm]可以表示為
1.2 基于PD(Proportional-Differential)控制的電磁軸承轉子系統的動力學方程
本文采用的是PD控制,控制電流可以表示為
式中:[kp]為比例控制系數;[kd]為微分控制系數。由比例控制所提供的電磁力起著抵消原位移負剛度的作用,并使系統在被矯正后具有一定的正剛度;微分控制部分相當于向系統提供正阻尼,從而使系統具有足夠的穩定性。
作用在每個磁極上的電磁力是電磁軸承內側的磁鐵的吸引力。根據圖1電磁軸承轉子受力示意圖可知,在[x]方向和[y]方向的電磁力的表達式為
2 近似解析分析
由于電磁軸承轉子系統動力學特性的非線性微分方程非常復雜。對它的高階非線性動力學方程只能求得高精度的數值解。但是數值解是不能完全代替近似解析解的,所以攝動分析方法成了研究非線性方程的重要工具。根據多尺度法,選擇1∶1的共振比情況進行研究和分析,設式(8)的解為
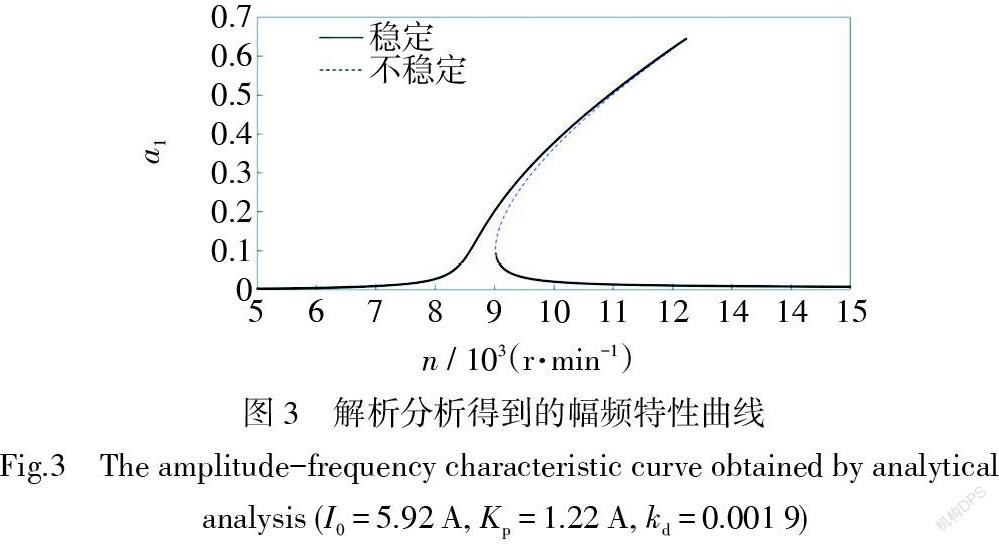
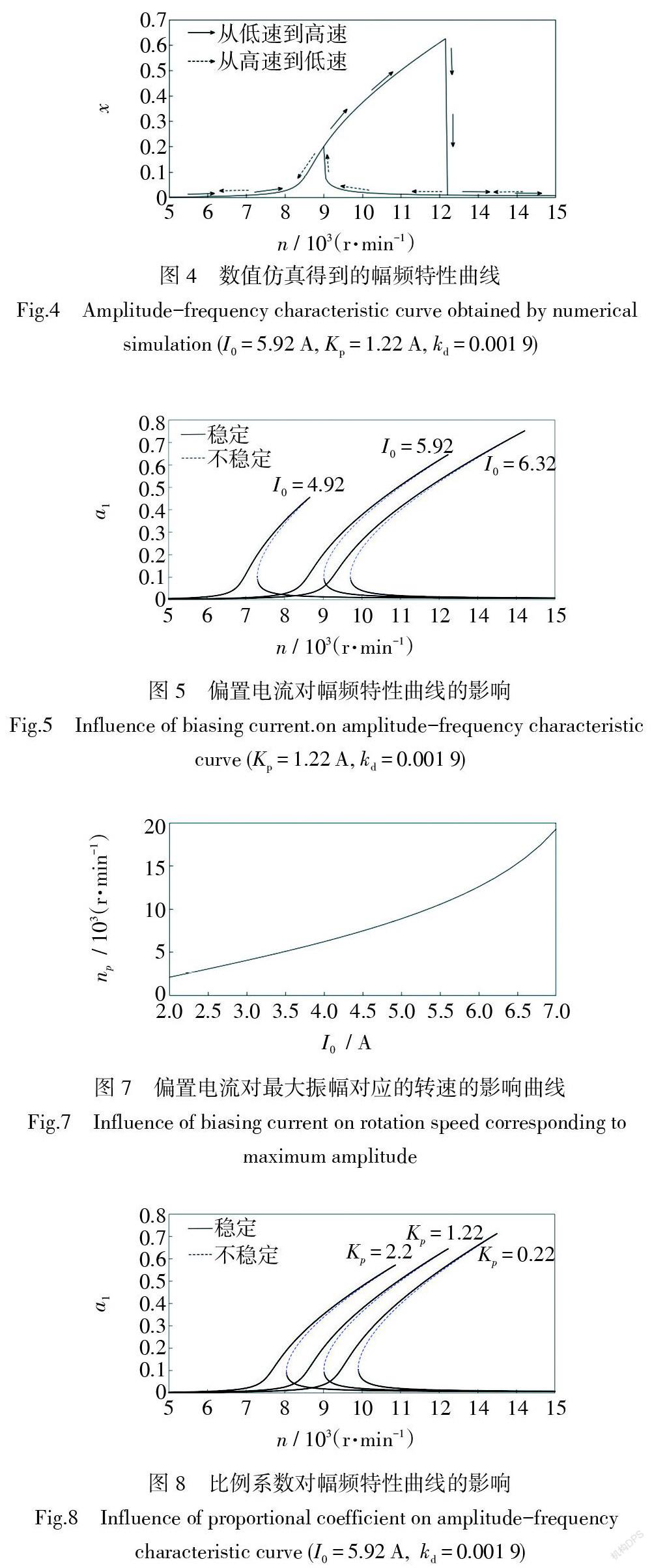
圖3是由多尺度法和同倫延拓法相結合得到的幅頻特性曲線,圖中實線代表穩定解,虛線代表不穩定解。圖4給出了根據無量綱化后得到的運動方程進行數值求解所得到的結果。通過圖4可以發現,當轉子轉速從低速逐漸上升時,如圖中實線箭頭所示,轉子的振幅由緩慢上升到加速上升,當達到一定值時發生跳躍現象,最終振幅趨于零,系統處于單穩態。同理,當轉子轉速從高速逐漸降低時,如圖中虛線箭頭所示,轉子的振幅開始緩慢增大,之后增大速度加快,達到一定值時,系統從雙穩態區域進入單穩態區域,振幅逐漸趨于零。比較圖3與圖4,可以看出兩者吻合較好。
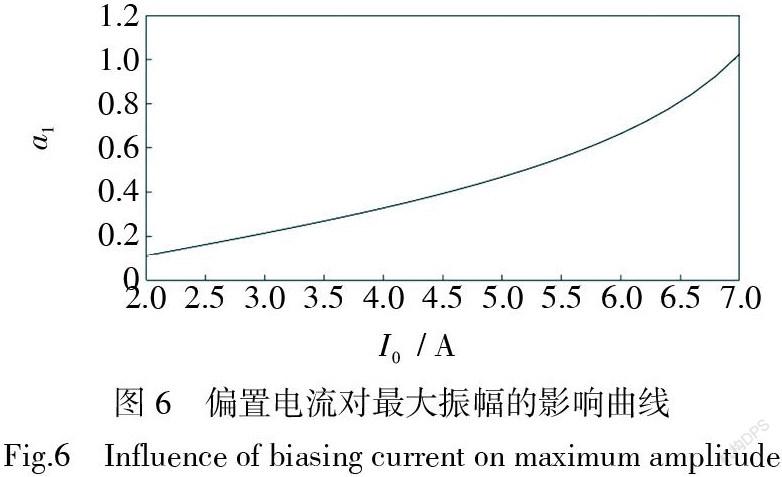
偏置電流對電磁軸承轉子系統振動性能的影響如圖5所示。從圖5中可以看出,減小偏置電流會使系統在較低的轉速下發生共振,但共振區域的最大振幅相對較小,系統雙穩態區域較小。反之增大偏置電流,會使系統在高轉速下出現共振,且共振區域的最大振幅相對較大,雙穩態區域也隨之增大。隨著偏置電流的增大,共振區域的最大振幅對應的轉速[np]也隨之上升。圖6和圖7為偏置電流對共振區域的最大振幅和最大振幅對應的轉速的影響曲線。由圖可知,隨著偏置電流的增大,共振區域的最大振幅和最大振幅對應的轉速也隨之增大。
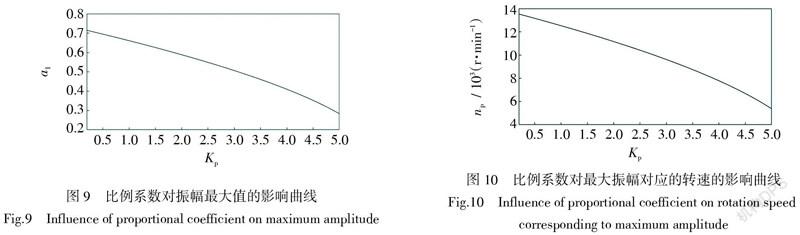
比例系數對電磁軸承轉子系統動態性能的影響如圖8所示。從圖中可以看出隨著比例系數的增大共振區域逐漸減小,共振區域的最大振幅和最大振幅對應的轉速都隨之減小。增大比例系數使系統在轉速低的情況下發生共振,共振區域減小。反之,減小比例系數使系統在較高的轉速下發生共振,共振區域的最大振幅增大,共振區域增大。圖9和圖10為比例系數對共振區域的最大振幅和最大振幅對應的轉速的影響曲線。由圖可知,隨著比例系數的增大,共振區域的最大振幅和最大振幅對應的轉速隨之減小。
3 結論
本文基于二自由度電磁軸承轉子系統的動力學方程,利用多尺度法對泰勒展開后的無量綱運動方程進行攝動分析,求得了關于系統振幅和相位的平均方程。利用同倫延拓法對平均方程進行求解,給出了系統的幅頻特性曲線,發現幅頻特性曲線表現出明顯的滯后現象,在升速和降速通過共振轉速時都會發生跳躍,利用數值仿真對解析計算的正確性進行了驗證。驗證結果表明數值計算的結果與解析解相吻合。研究了偏置電流和比例系數對幅頻特性曲線的影響,結果表明在其他參數一定的情況下,隨著偏置電流的增大,共振區域的最大振幅和最大振幅對應的轉速隨之增大。隨著比例系數的增大,共振區域的最大振幅和最大振幅對應的轉速隨之減小。
參考文獻:
[1]? ? SCHWEITZER G. 主動磁軸承基礎、性能及應用[M]. 虞烈,袁崇軍,譯. 北京:新時代出版社,1997.
[2]? ? SIVA SRINIVAS R,TIWARI R,KANNABABU C. Application of active magnetic bearings in flexible rotordynamic systems-A state-of-the-art review[J]. Mechanical Systems and Signal Processing,2018,106:537-572.
[3]? ? 魏金強. 磁懸浮軸承控制系統研究[D]. 武漢:武漢理工大學,2007.
[4]? ? JI J C,HANSEN C H. Non-linear oscillations of a rotor in active magnetic bearings[J]. Journal of Sound and Vibration,2001,240(4):599-612.
[5]? ? 李澤輝,滕萬慶,李翀. 磁懸浮儲能飛輪用徑向磁軸承磁路仿真分析[J]. 儲能科學與技術,2014,3(4):308-311.
[6]? ? 安華貞,楊曉東,張偉. 八極電磁軸承的非線性動力學研究[C]//第十六屆全國模態分析與試驗學術會議論文集. 天津,2016:130-132.
[7]? ? SHELKE S. Controllability of radial magnetic bearing[J]. Procedia Technology,2016,23:106-113.
[8]? ? 王媛. 電磁軸承—轉子系統的動力學行為分析[D]. 西安:西安理工大學,2009.
[9]? ? 劉熙娟. 電磁軸承—轉子系統的分岔研究[D]. 蘭州:蘭州交通大學,2016.
[10]? 張海燕. 電磁軸承-轉子系統的非線性動力學[D]. 北京:北京工業大學,2002.
[11]? 季進臣,虞烈. 電磁軸承轉子系統中高速不平衡轉子跌落過程的非線性動力學[J]. 機械工程學報,1999,35(5):62-66.
[12]? CHINTA M,PALAZZOLO A B. Stability and bifurcation of rotor motion in a magnetic bearing[J]. Journal of Sound and Vibration,1998,214(5):793-803.
[13]? 胡業發,周祖德,江征風. 磁力軸承的基礎理論與應用[M]. 北京:機械工業出版社,2006.
[14]? 胡磊. 電磁軸承及其控制系統的研究與設計[D]. 沈陽:沈陽工業大學,2017.
[15]? KASARDA M E F,ALLAIRE P E,NORRIS P M,et al. Experimentally determined rotor power losses in homopolar and heteropolar magnetic bearings[J]. Journal of Engineering for Gas Turbines and Power,1999,121(4):697-702.
[16]? JI J C. Stability and Hopf bifurcation of a magnetic bearing system with time delays[J]. Journal of Sound and Vibration,2003,259(4):845-856.
[17]? 胡海巖. 應用非線性動力學[M]. 北京:航空航天出版社,2000:57-59.
[18]? 虞烈. 可控磁懸浮轉子系統[M]. 北京:科學出版社,2003:37-61.
[19]? 劉熙娟,劉云,褚衍東,等. 一類軸承轉子系統的全局動力學行為分析[J]. 東北師大學報(自然科學版),2017,49(3):22-28.
[20]? 劉習軍,賈啟芬. 工程振動理論與測試技術[M]. 北京:高等教育出版社,2004:11-33.
[21]? 謝振宇,徐龍祥,李迎,等. 磁懸浮軸承轉子系統的穩定性及動態特性分析[J]. 機械科學與技術,2004,23(7):765-767,770.

