橫搖運動下養殖工船多液艙流場特性數值分析

方舟，徐紅昌，戴錦陽

(1.嘉興南洋職業技術學院，浙江 嘉興 314031；2.嘉興市港航管理服務中心，浙江 嘉興 314031)

自上世紀70年代開始，養殖工船總體構想[1]及大型養殖工船的系統[2]、總體設計[3]陸續展開，其中，液艙晃蕩是海洋工程領域中備受關注的熱點問題[4-6]。相關研究關注了液艙晃蕩對艙體結構的沖擊及疲勞影響[7-9]，較少有關于艙內水體流場特性的研究報道。養殖工船在風浪中的搖擺運動使得養殖艙內的水體發生劇烈運動，養殖艙內物理環境指標通常主要考慮水體流速及光照情況，而適養流速一般與魚體長度有關，如體長在20 cm以上的大黃魚，養殖艙內水體流速在0.6 m/s以下時對其影響較小。艙內適漁性問題，有學者研究了液艙晃蕩對養殖工船適漁性的影響[10-11]。而目前的研究大部分是通過在養殖內進行進水出水狀態下的流動特性研究[12-14]，而較少考慮養殖艙在船體運動激勵下的動態流場特性分析。為此，考慮基于CFD技術，對某10萬t級養殖工船橫搖運動下的養殖水艙液艙晃蕩現象分析不同橫搖頻率下的艙內流場特性。

1 理論基礎

計算養殖工船液艙內流體為不可壓縮連續流體，控制方程為連續性方程，采用k-ε方程湍流模型。液艙模擬為兩相流模擬，忽略各相之間的熱傳遞[15]，自由液面捕捉采用VOF方法。

1.1 控制方程

液艙液體為不可壓縮流體，連續性方程為

(1)

其動量守恒方程為

(2)

式中：p為流體微元的壓力，Fx、Fy、Fz為微元體上的質量力。

1.2 湍流模型

標準k-ε方程模型滿足湍流黏性系數各相同性，在該方程基礎上引入湍流動能耗散率ε的方程，因此k-ε方程為

Gk+Gb-ρε-YM+Sk

(3)

2 數值模型驗證

選取Mikelis[16]液艙晃蕩實驗驗證本文所采用的數值計算模型的正確性，液艙長、寬、高分別為0.741 m、0.399 m和0.395 m，液艙幾何模型以及橫搖中心Y1和Y2位置見圖1。液艙橫搖運動方程為φy=φ0sin(ωt)，φ0=0.1 rad。實驗中在寬度中心壁面處設置7個壓力監測點R1～R7，在寬度中心距離左側壁面0.135 6 m位置布置浪高儀WR。

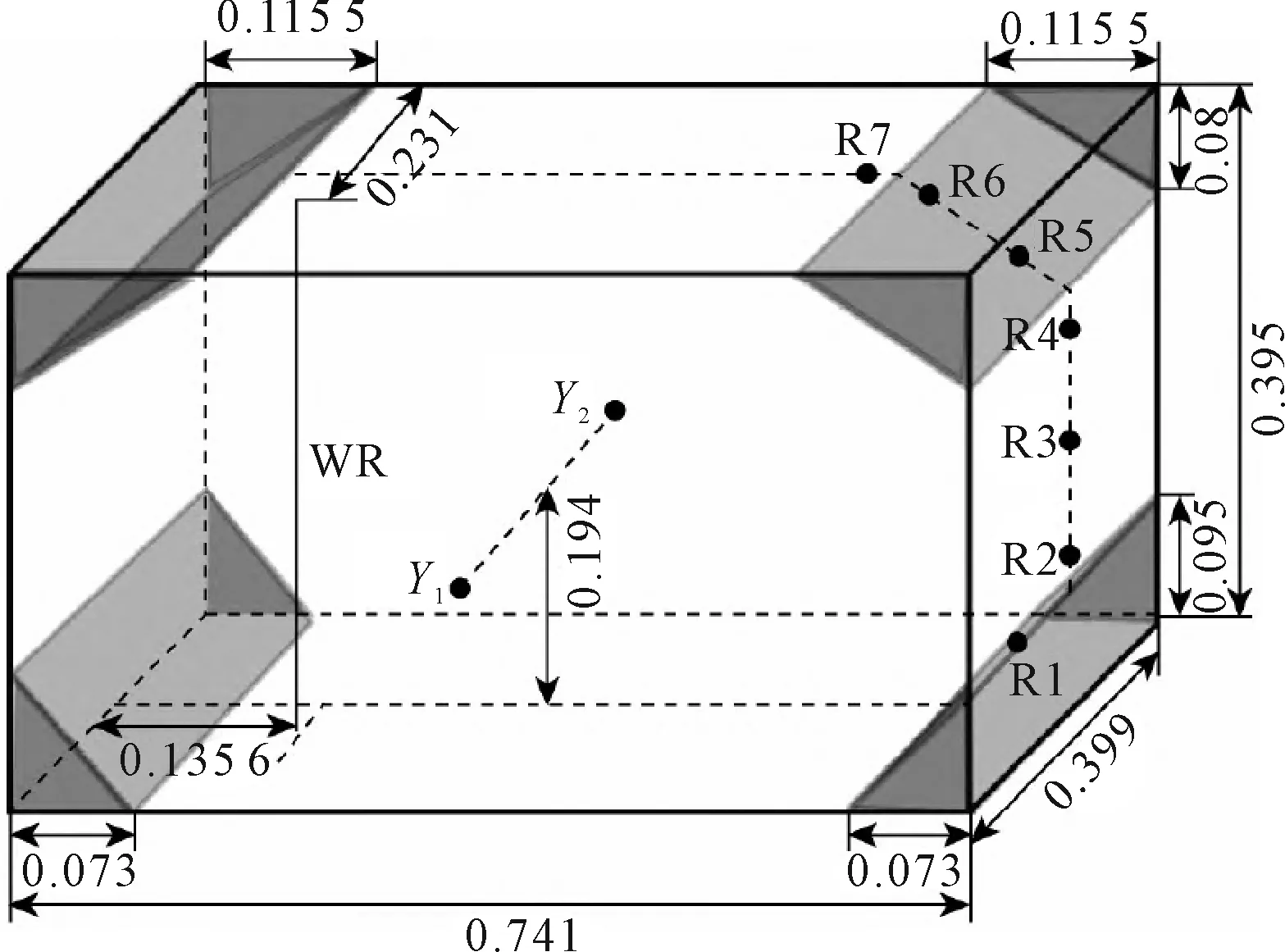
圖1 實驗采用液艙幾何模型

數值模擬中液艙所有邊界均設置為無滑移壁面邊界條件，模擬實驗中充液比為0.9，橫搖周期為0.97 s工況。在進行CFD數值計算時需要對網格進行收斂性分析[17]，選用滿足一定細化率要求的3組網格進行收斂性計算，3組網格尺寸劃分見表1，分別命名為Mesh a、Mesh b和Mesh c，3組網格R3監測點壓力及WR位置處的波高監測與實驗值對比分別見圖2和圖3。

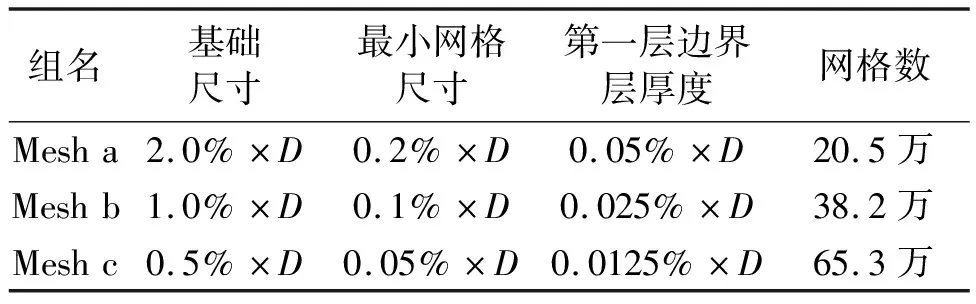
表1 網格劃分尺寸

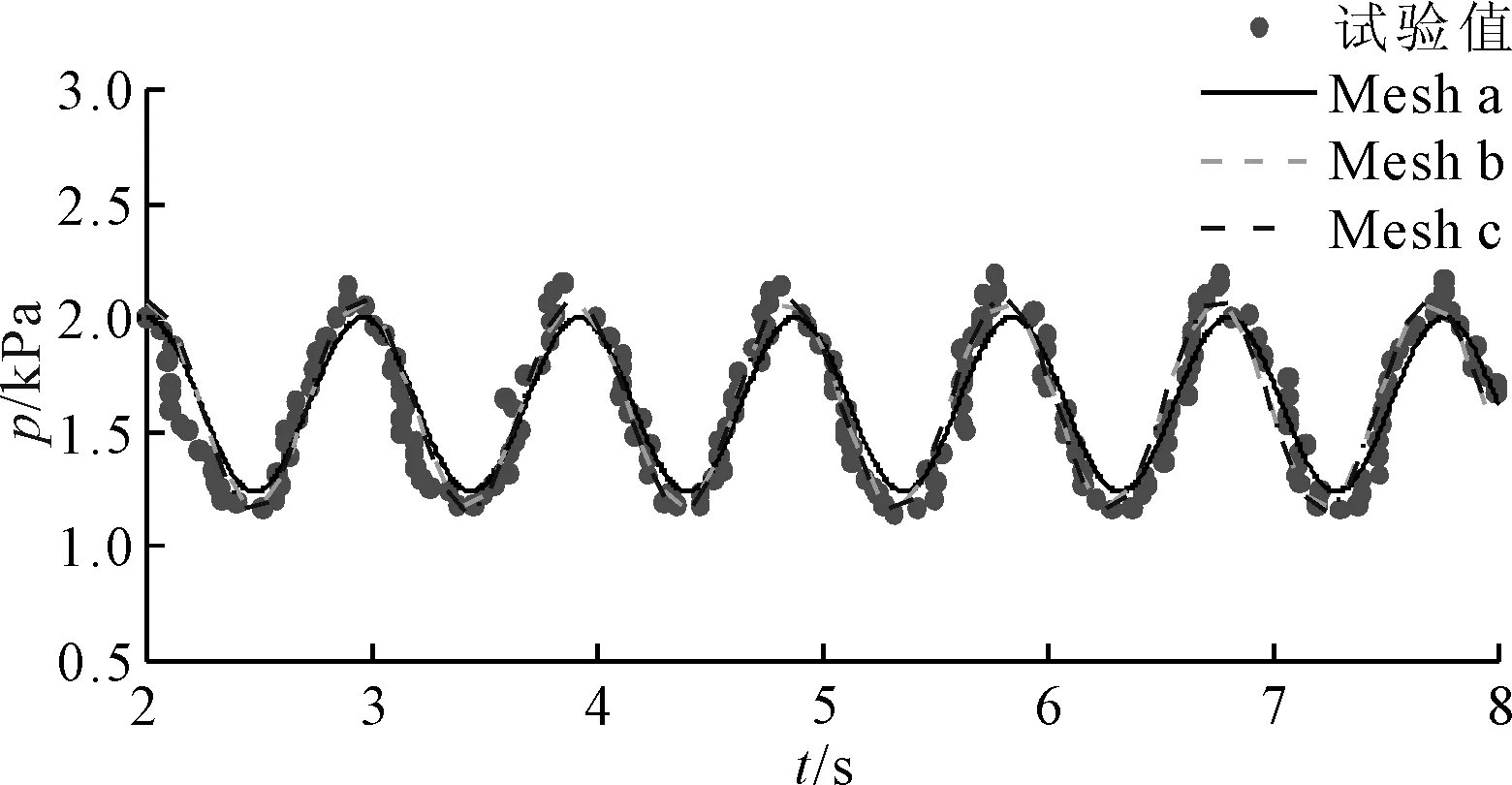
圖2 R3點壓力時歷曲線對比

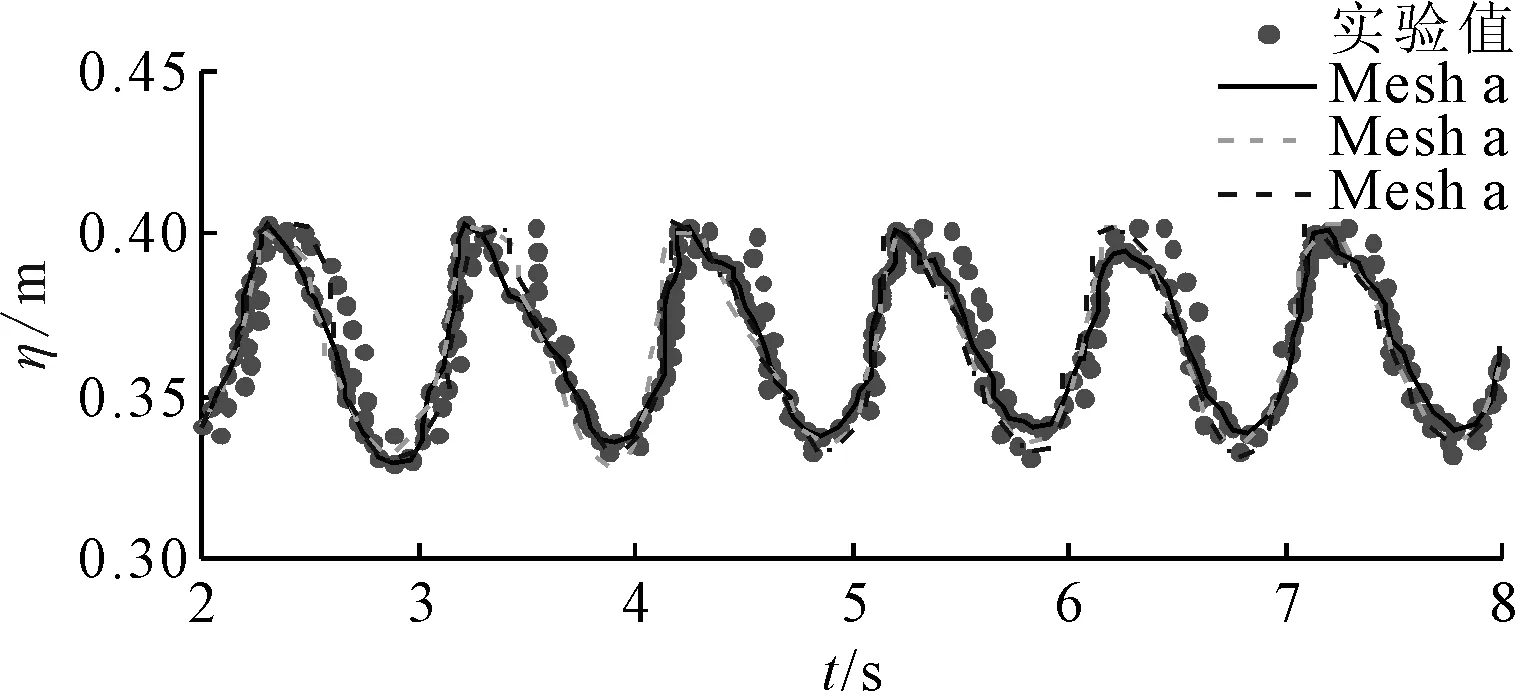
圖3 WR位置波面高度時歷曲線對比

從圖2和圖3中可以看出，3組網格計算得到的監測點壓力及浪高監測與實驗值對比吻合良好，雖然監測點峰值壓力與實驗結果略有差別，但隨著網格加密，數值計算結果與實驗值逐步趨近，驗證了本文所采用的網格的收斂性。由于所述某10萬t級養殖工船液艙形狀與實驗模型類似，因此后續計算中網格劃分采用相同方法進行劃分，網格尺度采用Mesh c。

3 計算模型

選取船首、船中2處典型位置養殖艙，見圖4。1號液艙關于中縱剖面對稱布置，長寬高分別為22.4 m、19.6 m和19.1 m；2號液艙在左舷，長寬高分別與1號液艙相同。所有液艙均裝載至距基線16.5 m高度處，液艙底部距船體基線高度均為2.4 m。

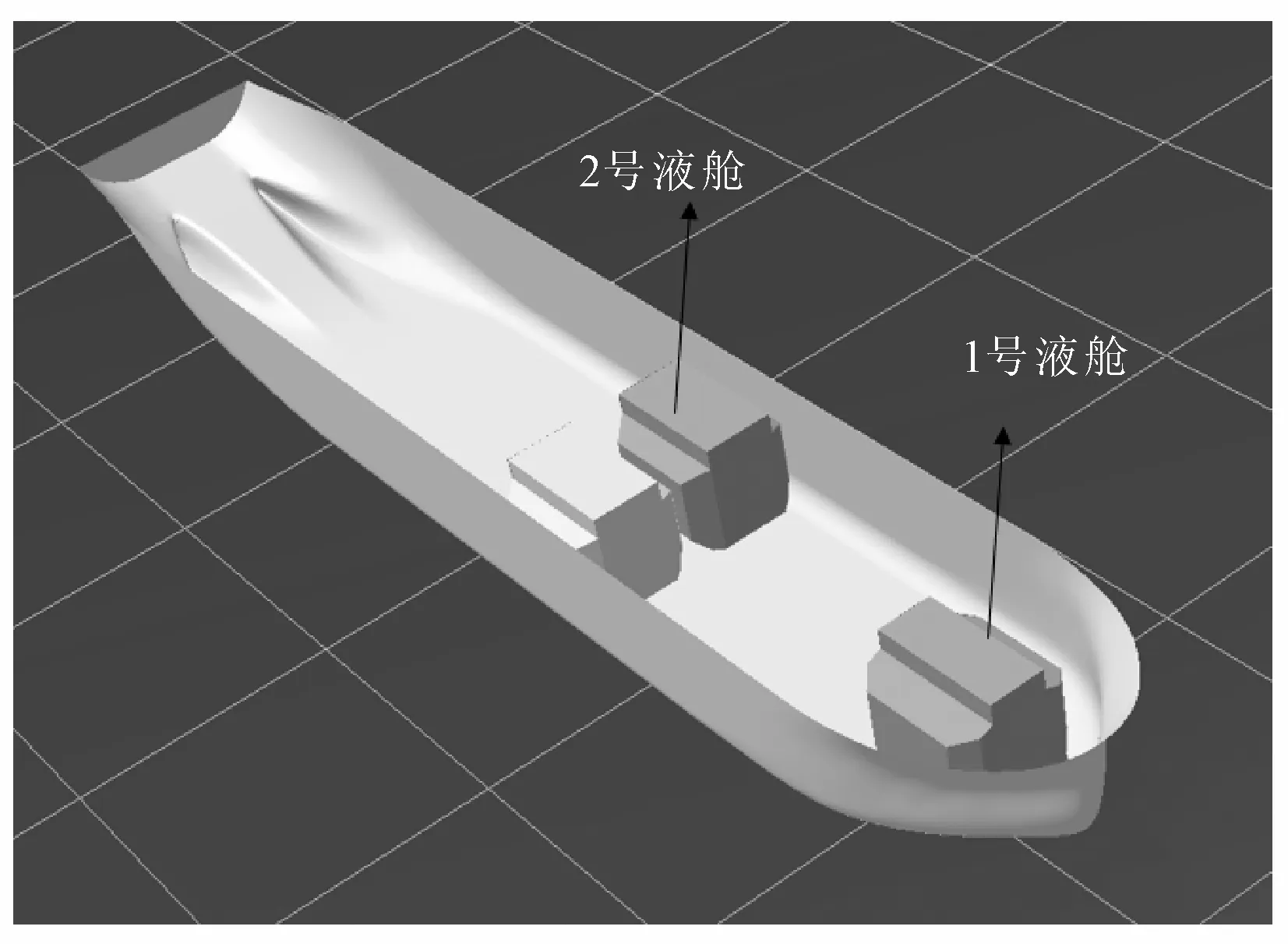
圖4 液艙幾何模型及布置位置

橫搖運動為船舶最主要的運動，因此計算中采用簡諧橫搖運動作為船體運動輸入，船體橫搖運動方程為

φ(t)=φ0sin(ω(t-Δt))

(4)

式中：φ為船舶橫搖運動角度；φ0為船舶橫搖運動幅值；ω=2π/Th，Th為船舶橫搖運動的周期；Δt為計算中設置的緩沖時間。船體主尺度參數見表2，選取船體重心位置為橫搖中心。

表2 船體主尺度參數 m

液艙網格采用前述Mesh c網格劃分方法，在自由液面附近進行網格加密處理，結果見圖5。

圖5 液艙網格劃分結果

選取2個液艙長度中心平面處不同位置處的監測點進行流速監測，監測點位置見圖6。

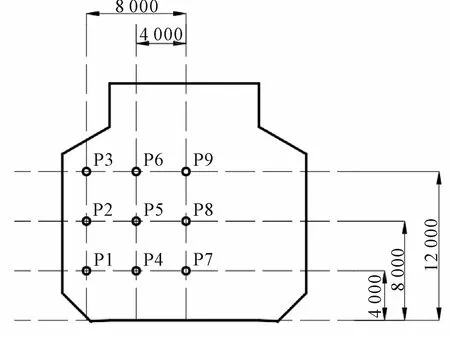
圖6 液艙監測點位置

4 結果分析及討論

4.1 單工況流場

以橫搖運動周期7.855 s，橫搖幅值5°為例，各液艙不同監測點位置處的流體速度時歷曲線見圖7。3個液艙的監測點流速整體具備一定的周期性，觀察發現3個液艙監測點處流速最大值由1號液艙到2號液艙呈逐漸增大的趨勢。2號液艙與1號液艙不同在于2號液艙布置并非沿船中對稱，因此艙內液體晃動幅度相對較大。

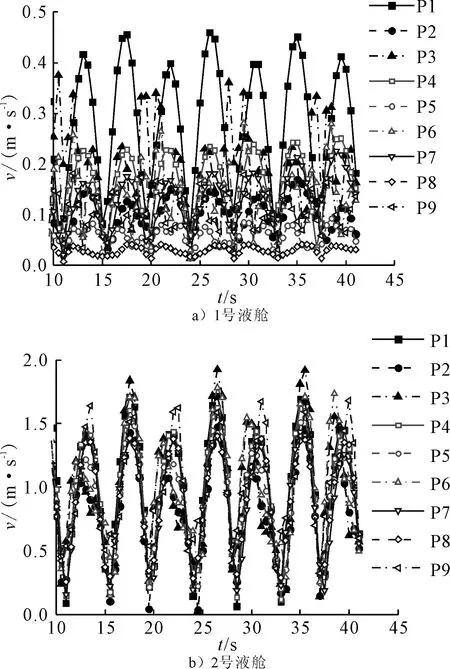
圖7 各液艙監測點速度時歷曲線

2個液艙受到的橫搖力矩時歷曲線見圖8，從圖8可以看出1號液艙由于沿船中對稱布置，因此橫搖力矩基本為0。而2號液艙布置在船體左舷，因此橫搖力矩為負值，力矩大小達到108量級，且呈一定的周期性變化，變化周期與運動周期吻合。

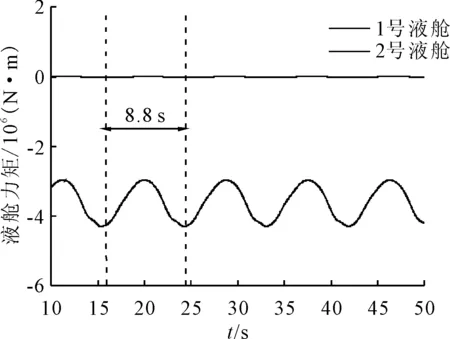
圖8 各液艙橫搖力矩時歷曲線

4.2 不同橫搖周期適漁性流速

養殖艙內水體流速對養殖艙的適漁性有重要影響，一般認為魚類適合養殖的流速范圍為

V=(1.19～1.66)L1/2

Vcr1=0.15+2.4L

Vcr2=2.3L0.8

(5)

式中：V為魚類適養流速的上下限范圍；Vcr1和Vcr2為養殖魚最大游動速度；L為養殖魚體長。以最常見的大黃魚為例，體長一般為20 cm，通過上式進行計算，得到適養流速為0.63 m/s。因此，本文以0.6 m/s作為養殖艙適養流速的上限。

同樣以橫搖運動周期7.855 s，橫搖幅值5°為例，液艙內適養流速占比(流速小于等于0.6 m/s)時歷曲線見圖9。

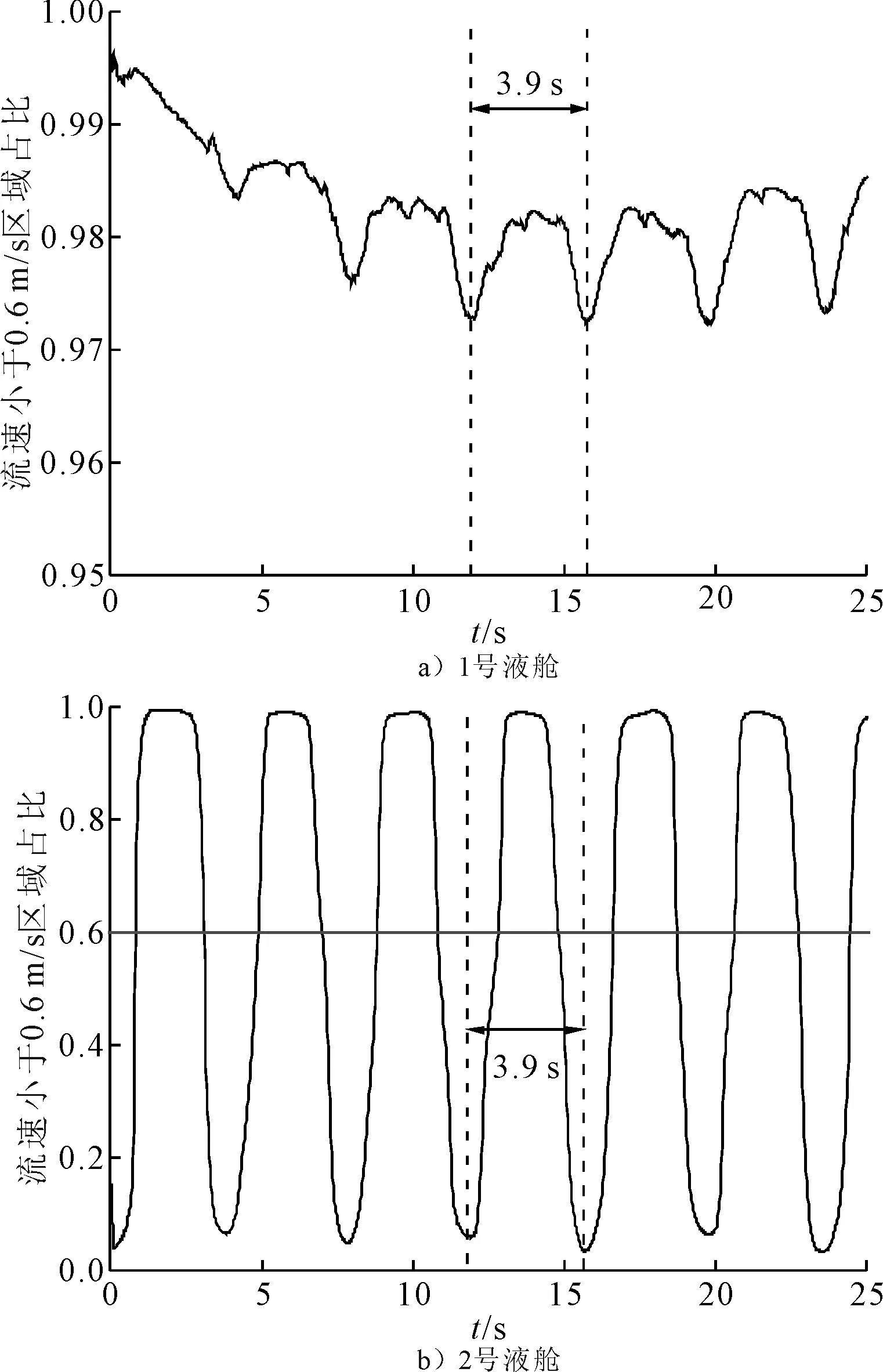
圖9 不同液艙適養流速占比時歷曲線

由圖9可見：不同位置處的液艙適養流速占比曲線均呈現一定的周期性，同時由于液艙晃蕩下流體的運動有一定的滯后性，因此在一個橫搖運動周期內相同位置處的流場速度變化會重復2次，因此適養流速占比曲線周期為橫搖運動周期的一半。1號液艙內適養流速占比均在97%以上，具有良好的適養性。而2號液艙內適養流速占比隨時間變化很大，最小為3.6%，最大接近100%，在1個周期內適養流速占比大于60%的時間大約為2 s，在1個曲線周期中的比例約為60%。

對于矩形液艙，其液體固有周期T為

(6)

式中：n為階數，這里僅計算一階頻率，n=1；L為液艙運動方向自由液面長度，L=19.6 m；H為充液深度,H=14.1 m；g為重力加速度。所述養殖水艙基本構型主干部分為矩形，因此用上述公式計算可能與實際有所偏差，但差別不大，計算得到橫搖方向一階固有周期為5.126 s。因此，重點關注養殖艙固有周期附近范圍內橫搖周期對養殖艙適漁性的影響。

不同橫搖周期下的液艙適養流速區域占比規律類似，采用與圖9相同的分析方法總結見表3。可以看出1號液艙的整體適養流速區域占比均在90%以上，這表明養殖艙對稱布置，養殖環境更加有利，且1號液艙適養流速區域占比隨著橫搖周期的增大而增大。2號液艙一個周期內適養流速區域比例超過60%的時間占比隨著橫搖周期的增大而增大，結合1號液艙結論，可以得出相同橫搖幅值時，橫搖周期越小，液艙內流體速度變化越劇烈，對養殖環境越不利。同時發現，養殖艙橫搖運動周期為5.126 s(橫搖固有周期)時，艙內適養流速占比并未出現明顯的降低。

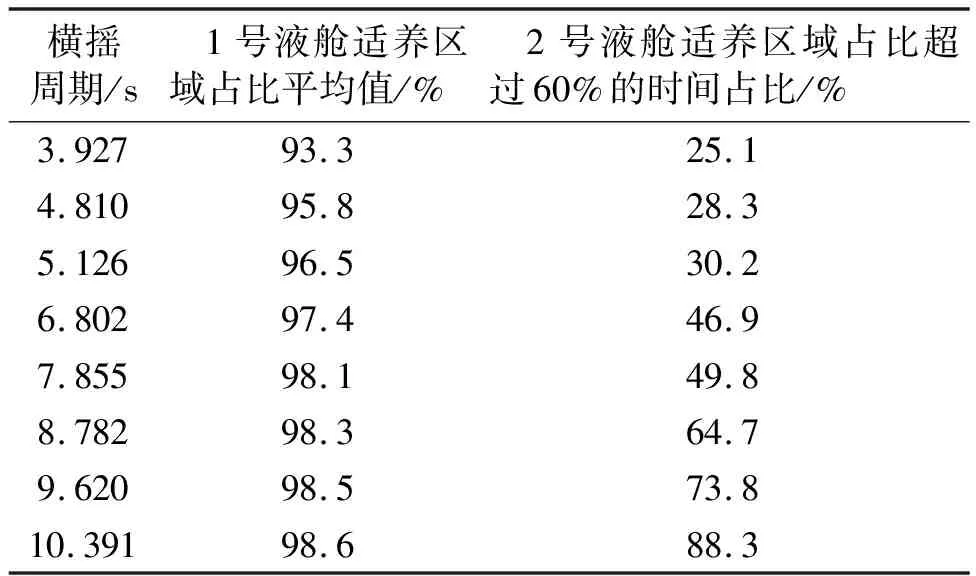
表3 液艙適養流速占比規律

4.3 不同液位高度適漁性流速

以橫搖運動周期8.782 s，橫搖幅值5°為例，對不同液位高度下養殖艙適漁性流速進行計算。3種液位高度對應距基線的距離分別為14.0 m(液艙肩部以下)、16.5 m(液艙肩部)和19.5 m(液艙肩部以上)，見圖10。

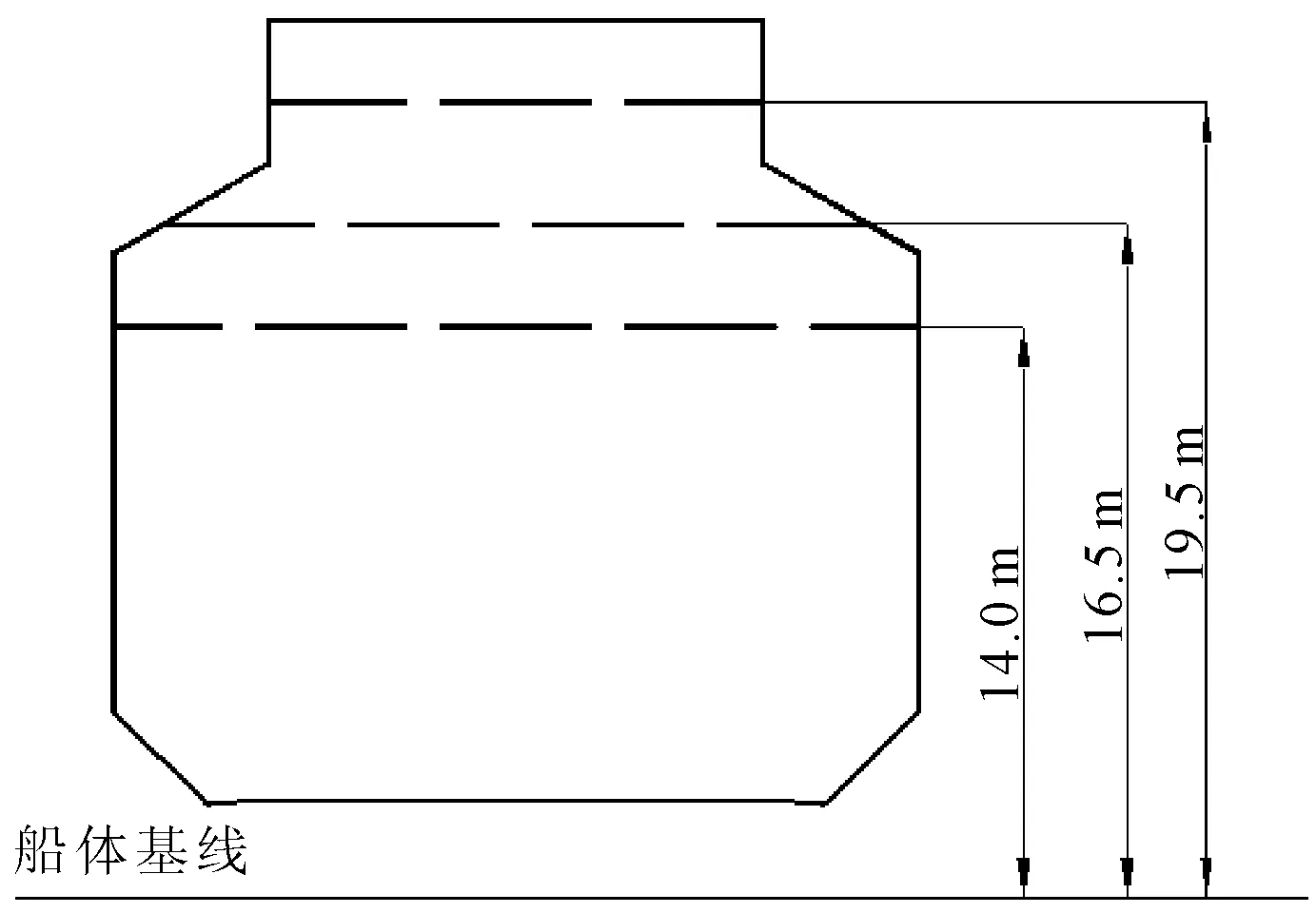
圖10 不同液位高度示意

不同液位高度下兩液艙流速小于0.6 m/s區域占液艙流體比例時歷曲線見圖11。

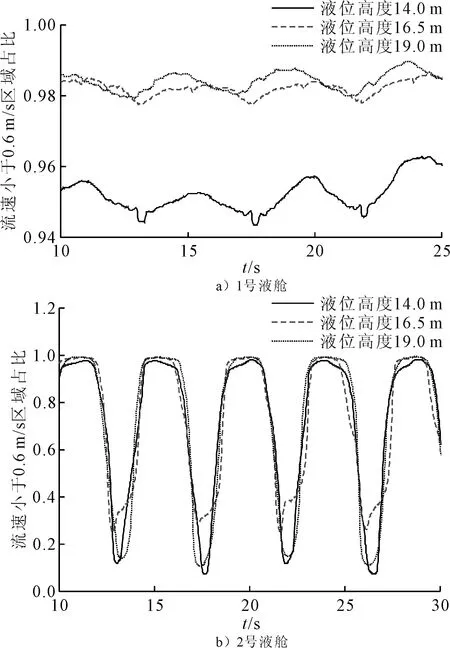
圖11 不同液位高度下液艙適養流速占比時歷曲線

1號液艙中3種液位高度下，液艙適養區域均在94%以上，且隨著液位高度的增大，適養區域占比也有一定增大。

2號液艙適養區域占比規律類似，從表4中可以看出，1個周期內適養區域占比超過60%的時間比例均相差不大。需要注意的是，液位高度為16.5 m時適養區域最小占比高于另外2種裝載情況，這表明養殖艙裝載位置為肩部區域時液艙內晃蕩程度較小。

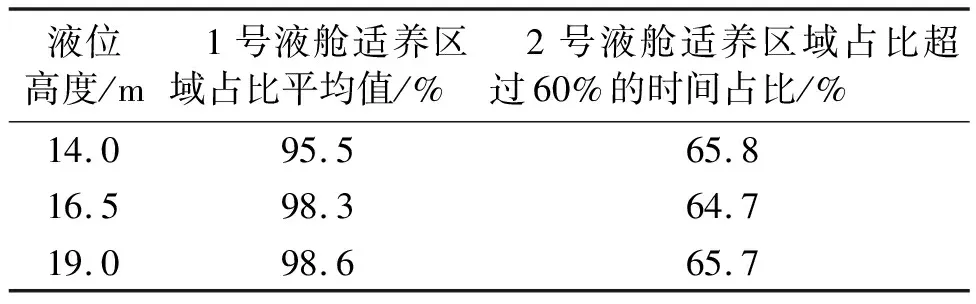
表4 不同液位高度液艙適養流速占比規律

5 結論

1)經過與實驗對比，驗證了所采用的數值計算模型的準確性，可以有效模擬液艙中的流場特性。

2)養殖艙沿船中對稱布置相比左右舷布置可以明顯的降低養殖艙內流體的晃蕩程度、減小液艙受到的力矩、提高養殖艙適養流速區域占比。

3)液艙適養流速區域占比時歷曲線具有一定的周期性，其周期大致為橫搖運動周期的一半。橫搖幅值相同時，隨著橫搖周期的增大，養殖艙內流體晃蕩程度減緩，養殖艙適養區域占比增大。

4)對于沿船中對稱布置的液艙，隨著養殖艙液位高度的增大，養殖艙適養區域占比也隨之增大。對于沿船體左右舷布置的液艙，養殖艙液位的高度對適養區域占比影響較小，但養殖艙裝載位置在肩部區域時，艙內流體整體晃蕩程度較小，是比較適宜的裝載高度。