最小二乘疊前時間偏移在川東南復雜構造成像中的應用

袁茂林

（中國石化勘探分公司油氣勘探管理部，四川成都 610041）

針對巖性油氣藏、復合型油氣藏以及隱蔽性油氣藏等復雜的勘探目標，不僅要求構造成像精確，而且對巖性成像提出了更高的要求。地震偏移技術在實際生產中存在如下問題：陸上震源子波時空變化劇烈、有限的波場帶寬、數據不規則及稀疏性等，這些客觀因素往往會導致偏移結果的振幅保真度和成像分辨率較低，難以滿足巖性解釋的需求。理論上，在油氣勘探領域被廣泛應用的互相關成像算子僅僅是正演算子的共軛，而不是它的逆。因此，常規的地震偏移只能對地下構造進行模糊成像，往往提供欠估計的反射系數信息。本質上，偏移成像是地下反射系數經過Hessian 算子濾波后的結果。為了消除Hessian 算子對成像結果的模糊化影響，可以將地震成像看作最小二乘框架下的線性波形反演（最小二乘偏移，LSM）問題，在數據空間域估計出分辨率較高、振幅信息可靠的地下反射系數的像，從而有利于后續的AVA/AVO 反演、疊前反演以及巖性解釋等工作。

Tarantola［1］早在1984年提出了基于最小二乘反演的地震成像思路。LeBras 和Clayton［2］、Lambare等［3］、Nemeth 等［4］以及Duquet 等［5］對最小二乘偏移技術進行了完善。但是，最小二乘偏移技術在工業界仍然沒有得到廣泛應用，影響其推廣應用的因素主要有兩個：一方面是計算效率較低，其計算工作量大約是常規地震偏移的N×2 倍（N是反演迭代的次數，次）［6-8］。另一方面，在實際資料處理中，子波問題、速度問題、資料信噪比問題、資料振幅一致性問題等等都會影響最小二乘偏移質量，尤其是實現最小二乘疊前深度偏移的難度非常大，主要原因如下：①陸地震源子波吸收衰減強，其時空變化劇烈，導致實際采集的地震記錄與模擬的地震記錄振幅匹配度較低［9］；②疊前深度偏移成像對速度模型的精度要求極高，高精度深度域速度模型建立已經成為深度域成像的最大難題［10］；③地震資料中存在的多種噪聲、多次波等干擾不在數據匹配的理論框架內，成為LSM 方法迭代反演難以有效收斂甚至不收斂的阻礙因素［11］。

基于以上分析，將一對互為共軛數學關系的疊前時間偏移及反偏移算子引入到共軛梯度的最小二乘反演框架中，通過編寫C 語言程序實現了最小二乘疊前時間偏移（LS-PSTM）技術。通過模型數據和實際資料處理驗證了本文方法可以有效壓制成像噪聲、提高成像分辨率以及補償常規偏移的成像振幅，在川東南復雜構造區具有良好的應用效果。

1 基本原理

在born 近似的線性化條件下，地震正演可以表達為如下矩陣的數學形式［12］：

其中，d為地震數據；m為地下的反射系數；L為疊前時間反偏移算子。

同樣地，線性化地震正演的共軛算子也可以寫成矩陣的數學形式：

此處，mmig表示反射系數的成像結果；LT為疊前時間偏移算子［13］。

將式（1）帶入式（2），得到

從式（3）可以看出，mmig是地下反射系數m經過Hessian 算子LT L濾波后的模糊成像，為了消除Hessian 算子LT L對地震成像的影響，可以將地震成像看作最小二乘框架下的線性波形反演問題，其目標是反偏移數據d與地震數據d0之間的誤差最小，從而最優化地估計出地下反射系數。定義如下目標誤差泛函［14］：

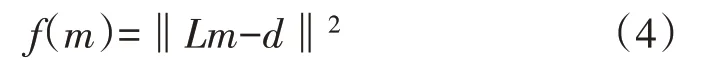
該泛函要求反演成像一定要使反偏移數據遵循地震數據的振幅變化規律，因此，數據預處理階段需要對數據進行單炮能量一致性校正。

為了求解式（4）所示的目標誤差泛函，可以采用共軛梯度類算法：

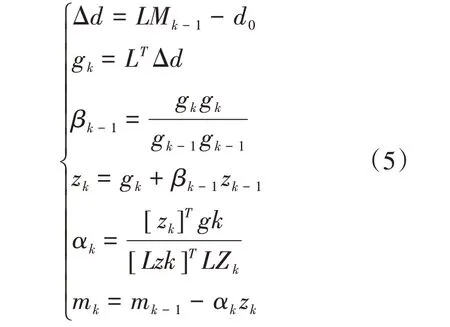
其中，Δd是數據殘差；mk（m0=0）是第k次迭代的反演成像結果；gk是梯度；βk-1為更正因子；zk為共軛梯度；αk為迭代的步長。當數據殘差減小到低于預設閾值時，迭代算法自動停止［15］。

LS-PSTM 技術流程如圖1 所示，從流程圖中可以看出，LS-PSTM 計算量為常規疊前時間偏移的N×2倍。

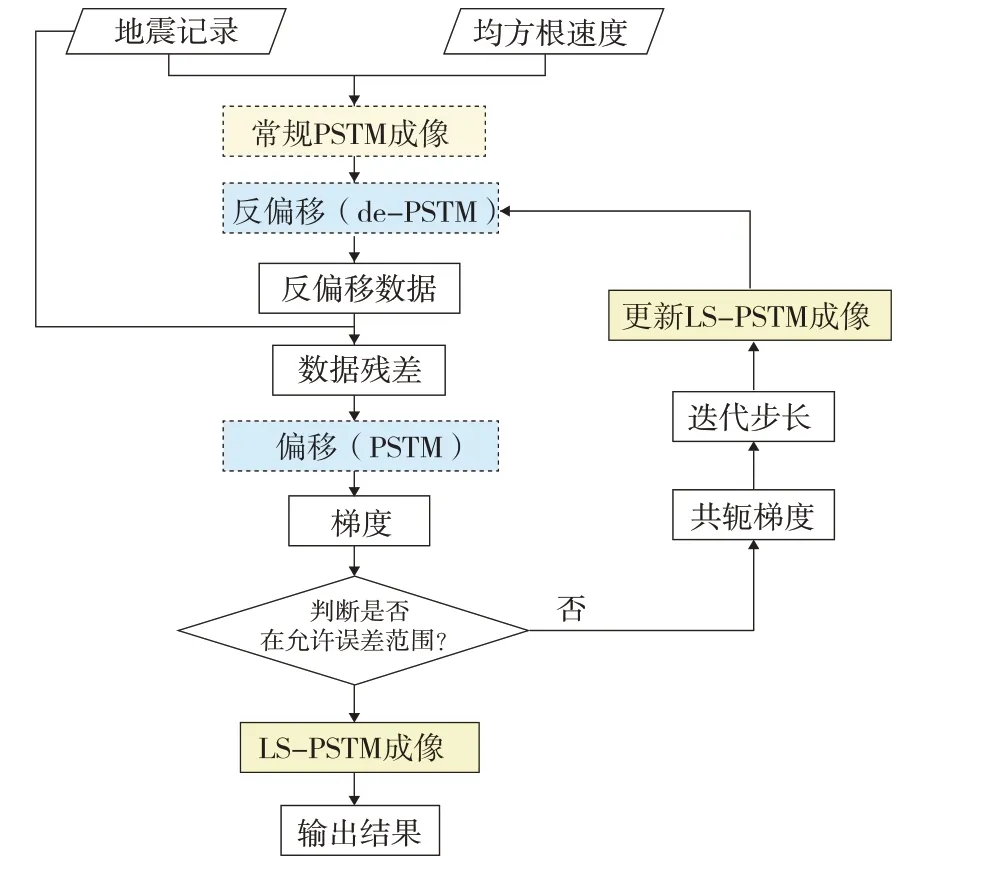
圖1 最小二乘疊前時間偏移技術流程

2 測試與應用

2.1 縫洞體模型測試

為了驗證本文發展的最小二乘疊前時間偏移技術的正確性、有效性和適應性，在編程實現LSPSTM算法的基礎上，采用縫洞體模型進行測試。

圖2a 為層速度模型，模型大小為1 000×2 001，縱橫向間隔為5 m，可以看到在兩個水平層下面有五個尺度大小不一的縫洞體，最小縫洞體尺度為5 m×5 m，縫洞體是異常低速度。圖2b 為迭代反演使用的均方根速度場。

圖2 速度模型

為了比較真實地模擬實際地震數據，采用波動方程高階有限差分算子進行正演。地震數據總共350 炮，炮間隔10 m，每炮151 道接收，道間隔10 m，每道有2 001個采樣點，采樣率2 ms。圖3是地震數據的單炮記錄，可以看出，除了有效的反射波和繞射波之外，記錄中還存在兩組多次波，分別來自第二層反射界面和縫洞體。

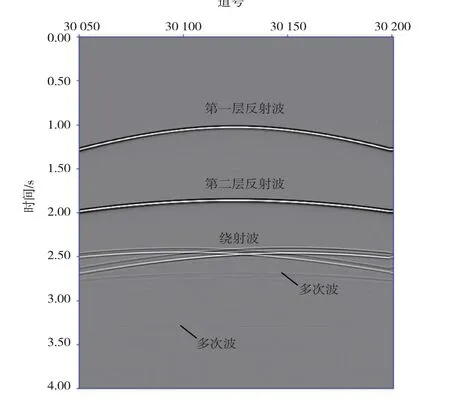
圖3 地震單炮記錄

根據式（5）所示的共軛梯度算法，采用上述模型和地震記錄進行LS-PSTM，并且在實際計算過程中隔炮隔道對數據進行抽稀。圖4a 和圖4b 分別為常規PSTM結果和LS-PSTM結果。

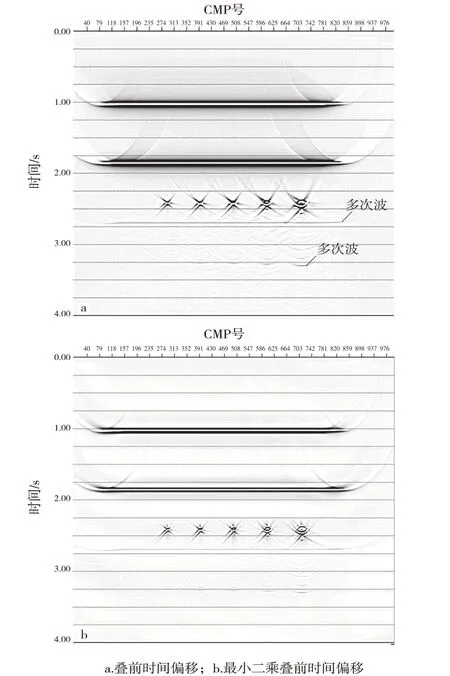
圖4 成像結果

可以看出，常規PSTM 成像分辨率較低，振幅不均衡，而且縫洞體成像能量聚焦性較差，且存在較嚴重的多次波成像和偏移噪聲。LS-PSTM 成像分辨率更高，補償了成像振幅，多次波和偏移噪聲在一定程度上得以壓制，縫洞體成像能量更加聚焦，縫洞體刻畫更加清晰，這一特點同樣可以延伸應用到斷裂、高陡構造側翼（傳播距離大、衰減多）以及小尺度巖溶縫洞體成像中。

為了定量地分析成像分辨率與成像振幅，接下來計算常規PSTM 和LS-PSTM 結果的頻譜。從圖5可以看出，常規PSTM 結果缺少反射的高頻成分，導致頻譜帶寬很窄，表明成像分辨率很低。此外，常規PSTM 成像振幅是欠估計的。相反，LS-PSTM 恢復了反射系數的高波數成分，拓寬了頻帶，并且沒有損失有效的低頻信息，表明LS-PSTM 能夠提高成像分辨率。而且，LS-PSTM 有效地補償了成像振幅，達到保幅成像的目的。

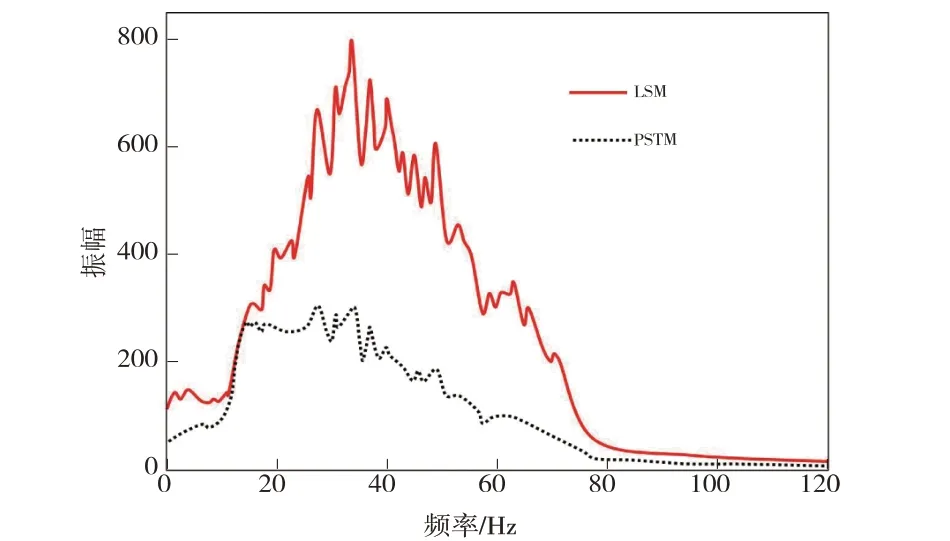
圖5 頻譜

收斂曲線是檢驗LS-PSTM 的有效指標。圖6是15 次迭代的反演收斂率曲線，可以看出，在最初的幾次迭代中，數據殘差降低得很快，接著收斂速度開始減慢，并且保持繼續降低的趨勢。然而，由于地震數據中存在嚴重的多次波干擾，導致迭代收斂速度明顯減慢。

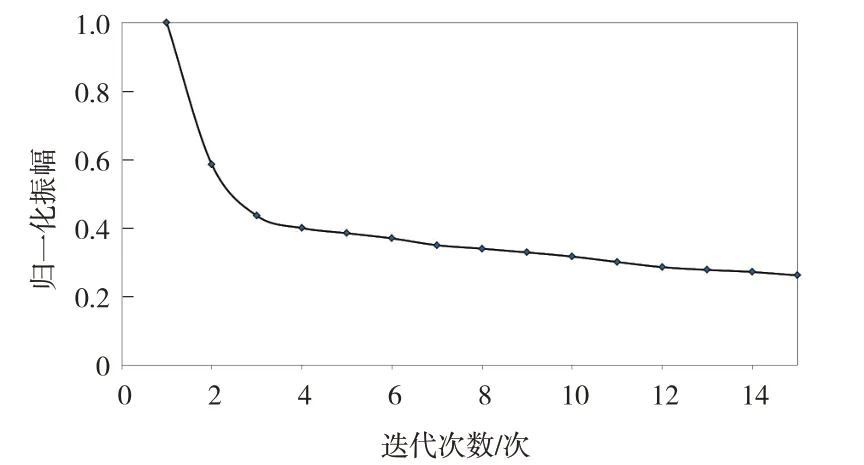
圖6 收斂曲線：數據殘差經過歸一化處理

2.2 川東南實際資料應用

為了分析驗證本文發展的最小二乘疊前時間偏移技術在實際生產中的應用效果，針對川東南巖溶縫洞儲層及高陡構造頁巖氣勘探，開展了實際地震資料處理。

2.2.1 巖溶縫洞體成像

川東南茅口組發育規模斷層巖溶縫洞體，油氣高產富集條件優越，是實現少井帶動高效勘探的有利目標。但是，實際地震資料目的層分辨率較低、振幅能量相對較弱，巖溶縫洞異常識別困難。

圖7a 是川東南實際資料常規PSTM 結果，圖7b是川東南實際資料LS-PSTM 結果。從圖7a 可以看出，常規PSTM 成像分辨率較低，振幅保真度較低，無法識別二疊系反射層（Tp2）茅口組巖溶縫洞儲層。從圖7b可以看出，LS-PSTM不僅提高了茅口組成像分辨率，突出了巖溶縫洞異常，巖溶縫洞體成像更加清晰，而且補償了成像振幅，保持了常規PSTM結果的波組特征和振幅強弱相對關系，層間信息更加豐富，能夠有效地支持巖溶縫洞地質評價工作。

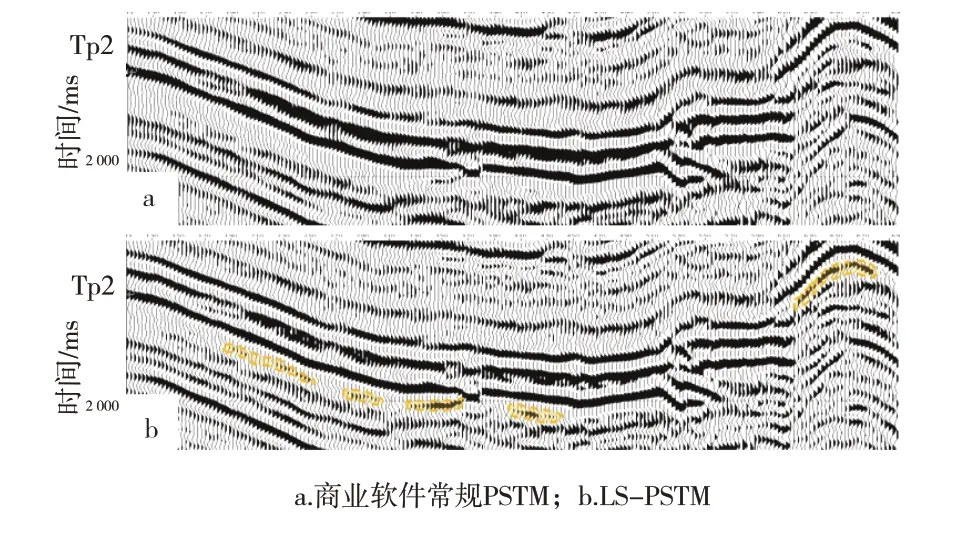
圖7 川東南實際資料地震成像

為了定量地分析成像分辨率與成像振幅，接下來計算常規PSTM 和LS-PSTM 結果的頻譜。從圖8可以看出，PSTM 結果的主頻為26 Hz，缺少反射系數的高頻成分，導致頻譜帶寬很窄，表明成像分辨率很低。相反，LS-PSTM 恢復了地下反射系數的高頻成分，且沒有損失低頻成分，拓寬了頻帶，并且地震資料的主頻提高至31 Hz，表明LS-PSTM 能夠提高成像分辨率。

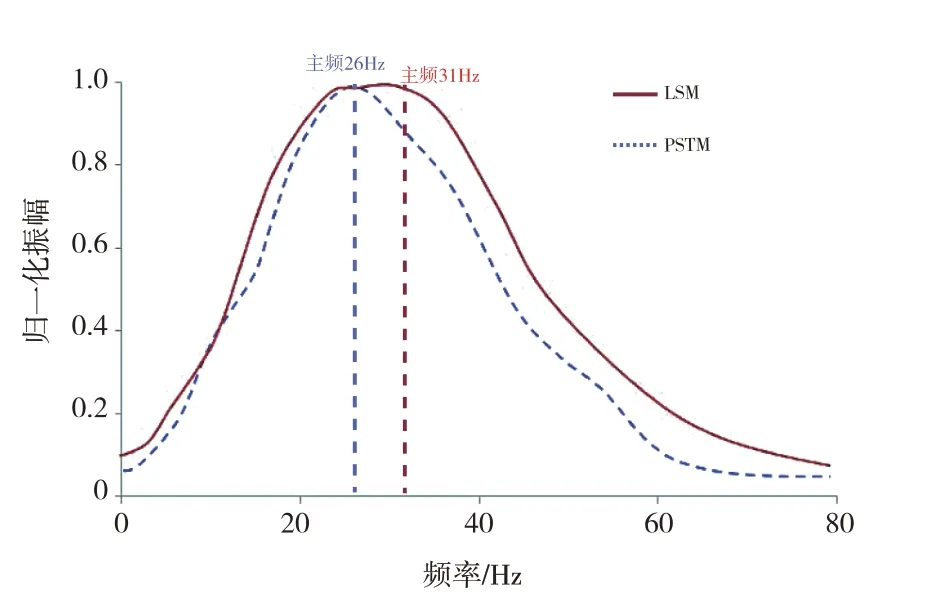
圖8 頻譜對比

圖9 是20 次迭代反演的收斂率曲線，收斂曲線是檢驗LS-PSTM 穩定性的有效指標。從圖9 可以看出，在最初的幾次迭代中，數據殘差降低得較快，接著收斂速度開始減慢，并且保持繼續降低的趨勢，說明LS-PSTM過程是穩定且收斂的。

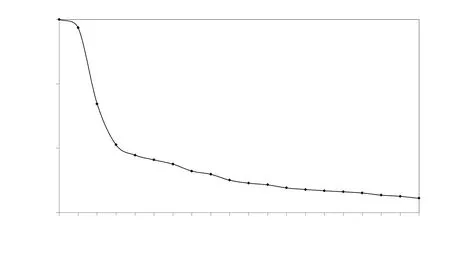
圖9 收斂曲線：數據殘差經過歸一化處理

2.2.2 高陡構造成像

川東南高陡構造鉆井、野外露頭顯示，高陡構造主體具有較好的頁巖氣勘探潛力。但是，由于受多期構造運動的影響，構造變化劇烈，地層傾角變化大，地層速度縱橫向變化快，地震波場極其復雜，地震成像困難。

圖10 是川東南高陡構造成像處理結果，圖10a是商業軟件常規PSTM 結果，圖10b 是LS-PSTM 結果。對比可以看出，LS-PSTM 壓制了偏移噪聲，改善了高陡構造成像質量，高陡構造內幕波組特征更加清晰，斷背斜頂部成像較完整，有利于志留系（Ts）頁巖氣保存條件評價工作。此外，向斜區Ts 反射層波組連續性好,斷層位置更加明確，基底斷裂成像分辨率更高（圖中黑色虛線方框所示），有利于二疊系茅口組儲層評價工作。

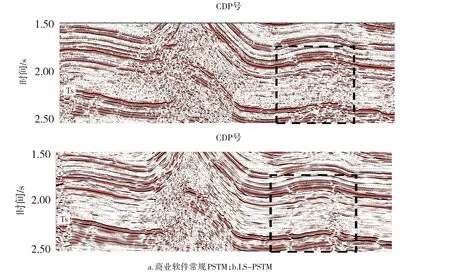
圖10 川東南實際資料地震成像

3 結論與認識

將地震成像看作最小二乘框架的反演成像問題，構建了互為共軛關系的偏移/反偏移算子，利用共軛梯度法進行最小二乘疊前時間偏移（LSPSTM），在數據空間域計算出分辨率較高、振幅信息可靠的地下反射系數的像。通過縫洞體模型數據測試驗證了LS-PSTM 技術的正確性和有效性，相比于常規PSTM，更能夠提高成像信噪比、成像分辨率以及振幅保真度。

將LS-PSTM 技術應用于川東南實際資料處理中，取得良好的應用效果。①LS-PSTM 提高了二疊系茅口組成像分辨率，突出了巖溶縫洞異常；②LSPSTM 改善了高陡構造成像質量以及向斜區志留系反射層波組連續性，并且提高了向斜區基底斷裂成像分辨率。

隨著勘探目標日趨復雜，實際生產對地震成像精度的要求越來越高。LS-PSTM 技術展現了解決復雜構造成像難題的能力，伴隨計算機運算能力不斷提升，LS-PSTM 技術具有良好的推廣應用前景。