SRTM與ASTER加權融合的機器學習方法

鄭婷婷，陳傳法，張照杰

(1.山東科技大學 測繪與空間信息學院，山東 青島 266590；2.浙江正元地理信息有限責任公司，浙江 湖州 313200)

0 引言

數字高程模型(digital elevation model，DEM)作為國家空間數據基礎設施的主要數據之一[1-3]，廣泛應用于水文分析、森林清查、土地利用分類等領域[4]。SRTM(shuttle radar topography mission)和ASTER(advanced spaceborne thermal emission and reflection radiometer)是兩種免費的覆蓋全球大部分地區的DEM數據集，ASTER由光學影像制成，數據易因云層覆蓋、薄霧遮擋等天氣影響產生無效值[5]；而SRTM由雷達影像制成，受天氣影響小，但數據易因起伏地形影響導致空缺，存在雷達陰影[6]、相位解纏[7]等技術問題。光學影像和雷達影像原理制成的DEM優勢互補，為DEM融合提供了可能性，因此，充分結合SRTM和ASTER各自的優勢，進行有效的數據融合，是充分挖掘現有DEM數據集信息并得到更高質量的DEM的一種有效途徑。

目前，國內外學者已經開展了DEM數據融合的相關研究。例如，沈煥鋒等[8]基于高差擬合神經網絡和TIN差分曲面方法生成了高質量的空間無縫DEM，但利用神經網絡模型擬合ASTER的誤差分布是對單個DEM質量進行改善，而且SRTM數據的空洞填補只是一種數據替換，在DEM融合過程中沒有考慮綜合光學技術和雷達技術的優點。Schultz等[9]基于自一致性技術實現了DEM數據的有效融合，但融合數據都是光學影像，在數據融合過程中無法克服光學技術獲取DEM的缺陷。Papasaika等[10]基于一個通用的使用稀疏表示框架的方法實現了兩個任意DEM的有效融合，但融合方法數學推導嚴密、不易理解。陳傳法等[11]基于快速傅里葉變換實現了SRTM和ASTER的有效融合，但濾波閾值選取過程繁瑣，融合效果依賴選擇的濾波器，并可能存在細節信息丟失問題。考慮到不同地貌對高程精度的影響，Tran等[12]基于地貌分類采用不同權重實現了SRTM和ASTER的有效融合。在此方法基礎上，孟偉等[13]進一步提出了地貌過渡區消除地貌分界線兩側的高程突變，但DEM融合選擇的是整體權重，忽略了單個像元對DEM精度的影響。Pham等[14]提出了一種融合SRTM和ASTER有效估計缺少參考數據區域地形的方法，但DEM精度不僅只與坡度相關，還受坡向、地形起伏度等其他地形因子的影響。Bagheri等[15]通過神經網絡模型預測TanDEM-X和Cartosat-1融合權重的方法得到精度更高的DEM，但是該方法僅以城區作為實驗區，沒有考慮在復雜地形是否有效。

為了提高SRTM和ASTER的融合質量，綜合兩種數據集的優勢，充分考慮地形因子同時對DEM精度的影響，本文提出了一種顧及地形因子的神經網絡模型的加權融合方法，并以黃土高原典型地貌董志塬區域為研究區驗證方法的可行性和有效性。該方法的優勢為充分考慮了地形因子對DEM誤差的影響，并采用神經網絡描述它們的非線性關系。

1 研究區與數據源

本文研究區域為甘肅省慶陽市境內中南部的董志塬地區，在涇河北岸、馬蓮河和蒲河兩大河流之間，面積為2 765.50 km2，高程范圍為1 050～1 410 m，經緯度范圍為107.46°E～107.96°E、35.26°N～36.06°N。SRTM為C波段傳感器干涉測量獲取的30 m分辨率的SRTM 1數據，ASTER為對地觀測衛星Terra獲取的立體像對生成的30 m分辨率ASTER V2版本數據。研究區SRTM和ASTER數據均來源于美國國家地質調查局網站(http：//earthexplorer.usgs.gov/)，平面基準為WGS84，垂直基準為EGM96。本文獲取了高精度控制點為參考數據，點數約為10 000個(圖1)，控制點均勻覆蓋整個研究區，平面基準為北京54坐標系統，垂直基準為1985國家高程基準。

圖1 研究區數據

2 研究方法

本文提出了一種基于地形因子預測融合權重的加權融合方法，充分考慮每個像素的地形因子對DEM融合的影響，而不是簡單地按地形分類對DEM數據進行融合[16]。首先對DEM數據進行預處理，利用ArcGIS軟件提取控制點的橫縱坐標、坡度、坡向、坡位、地形起伏度等地形因子，并將控制點隨機分為90%的訓練集和10%的測試集；然后利用訓練集與DEM高程差值和地形因子之間的非線性關系訓練出神經網絡模型，再以DEM的空間位置和地形因子為網絡輸入，利用神經網絡模型分別對SRTM和ASTER高差分布進行預測，依據DEM預測高差和融合權重計算公式得到SRTM融合權重圖；最后將SRTM和ASTER加權融合后得到融合DEM，并進行質量評估。本文實驗流程如圖2所示。

圖2 SRTM和ASTER數據融合流程圖

2.1 數據預處理

為了消除高程系統帶來的系統偏差，對DEM數據與控制點進行坐標系和高程基準統一。首先，統一投影坐標系為Beijing_1954_3_Degree_GK_Zone_36；其次，統一高程基準為1985國家高程基準。根據郭海榮等[17]的研究成果可知，1985國家高程基準與WGS84定義的似大地水準面之間有0.357 m的垂直偏差，故SRTM和ASTER的高程均加上0.357 m。

2.2 神經網絡模型與融合權重確定

神經網絡是一種應用類似于大腦神經突觸連接結構進行信息處理的數學模型，BP神經網絡(back propagation neural network，BPNN)是一種誤差反向傳播的多層前饋神經網絡，由輸入層、隱藏層和輸出層組成，遺傳算法通過優化BPNN的初始權值和閾值，從而優化了網絡模型的結構。神經網絡的非線性預測能力可用于探究高程值與地形因子之間的關系[18]。在前人的研究基礎上[19]，綜合考慮影響高程誤差空間分布的關鍵因素，并結合研究區特征以及數據可獲取情況，本文選取橫縱坐標、坡度、坡向、坡位、地形起伏度六個地形因子作為網絡模型輸入數據。其中，橫縱坐標作為空間位置信息輸入，坡度、坡向、坡位、地形起伏度作為地形信息輸入；為了避免高精度控制點與DEM高程值存在的共線性問題，本文以二者高程差值作為網絡模型輸出。

首先，以訓練集的橫縱坐標、坡度、坡向、坡位、地形起伏度(5×5的窗口)六個地形因子作為網絡輸入，DEM高程差作為目標輸出，對BPNN預測模型進行訓練。輸入層與輸出層神經元個數分別是6和1，隱含層可設置為單隱層和多隱層，在網絡精度達到要求的情況下，優先選擇單隱層；根據Gardner等[20]研究成果，隱藏層神經元個數在6～13之間，經過反復嘗試本文設置為12。另外，隱藏層和輸出層的轉換函數分別選擇tansig和purelin函數，訓練函數選擇為trainlm函數。神經網絡預測模型如圖3所示。

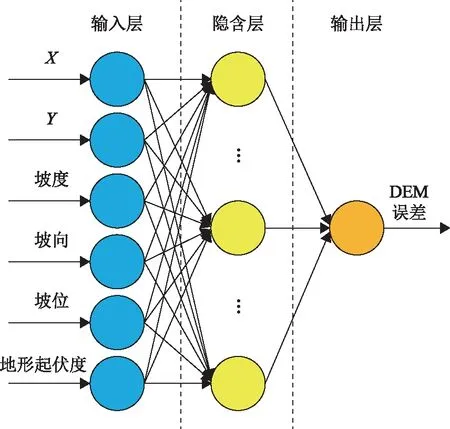
圖3 神經網絡預測模型結構示意圖

融合DEM計算如式(1)所示。

(1)

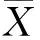
(2)

式中：ei為研究區；SRTM第i個像元的預測高程誤差；ej為研究區ASTER對應像元的預測高程誤差。

2.3 精度評價方法

本文采用檢查點法對融合前后的DEM數據進行定量評價，選擇平均絕對誤差(MAE)、中誤差(RMSE)和標準差(SD)三個指標對高程誤差進行統計。標準差反映了研究區測試集與DEM高程差值的離散程度，中誤差對異常高程敏感，平均絕對誤差能更好地反映預測值誤差的實際情況。若誤差中不包含系統誤差，則中誤差接近于標準差。

3 實驗結果

3.1 DEM精度分析

基于神經網絡模型和式(1)～式(2)可得到SRTM融合權重圖(圖4)。由圖4可知，SRTM融合權重圖在空間上分布不均勻，研究區南部地區以及北部地區的溝壑部分明顯權重較高，大于0.8，西北邊緣地區權重明顯較低，約在0.2左右，中部地區權重約0.6左右，其他地區權重則大小不一。對SRTM和ASTER加權融合得到融合DEM(圖5)。

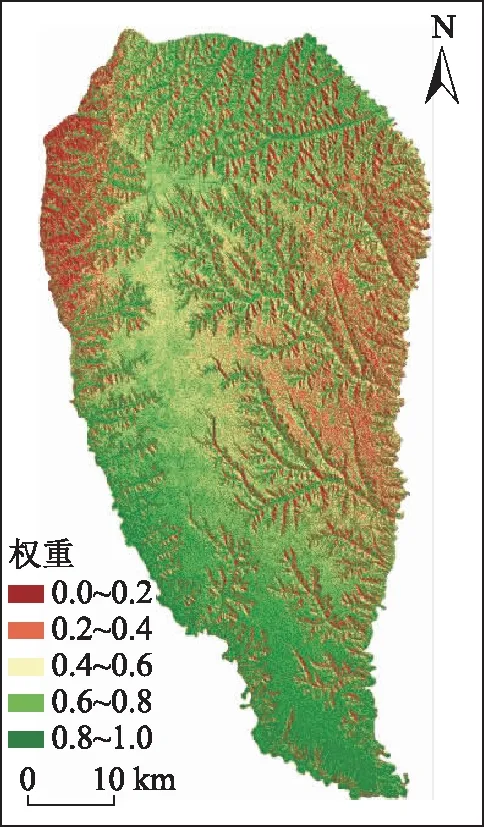
圖4 SRTM融合權重圖

圖5 融合后DEM

由表1可知，SRTM精度高于ASTER，融合后DEM比二者精度更高。融合后DEM平均絕對誤差相比于SRTM和ASTER分別降低了1.29 m和3.66 m，中誤差分別降低了0.40 m和3.16 m，標準差分別降低了0.79 m和2.07 m。

表1 不同DEM精度指標 m

3.2 地形因子對DEM精度影響分析

為了探究各地形因子對DEM高程精度的影響，本文首先從SRTM中提取坡度、坡向、坡位和地形起伏度，并采用自然間斷點分級法將坡度劃分為五級：0～7.4°(Ⅰ級)、7.4°～15.7°(Ⅱ級)、15.7°～23.8°(Ⅲ級)、23.8°～32.7°(Ⅳ級)和32.7°～64.7°(Ⅴ級)；將坡向平均劃分為四類：-1°～90°(NE)、90°～180°(SE)、180°～270°(SW)和270°～360°(NW)；然后基于Weiss[21]研究方法將坡位分為山脊、上坡、中坡、平坡、下坡和谷底六類；再將地形起伏度按0～20 m、20～40 m、40～60 m、60～80 m和80～153 m分為五類，以測試集高程為標準，SRTM、ASTER和融合DEM數據各類型高程誤差標準差統計結果見圖6。

由圖6(a)可知，SRTM、ASTER和融合后DEM各坡度等級誤差均隨坡度增大而增大，最大可分別達到20.16 m、18.48 m和17.19 m；SRTM誤差隨坡度增加幅度在三者中最大，說明SRTM受坡度影響最大，融合后DEM誤差在Ⅲ、Ⅳ和Ⅴ等級中比SRTM、ASTER小，說明坡度對DEM高程精度的影響在融合之后得到降低。

圖6 研究區不同地形因子DEM誤差統計

由圖6(b)可知，SRTM、ASTER和融合后DEM在NE、NW高程誤差較大，SE、SW較小。相比于ASTER，融合后DEM各坡向類型高程誤差均得到明顯降低，NE、SE、SW、NW高程精度分別提高了2.19 m、2.24 m、2.06 m和2.4 m；SRTM各坡向類型高程誤差均低于ASTER，融合后DEM在NE、SW、NW精度均高于SRTM，說明SRTM和ASTER數據融合削弱了坡向對DEM高程精度的影響。

由圖6(c)可知，各坡位類型高程誤差從大到小分別是谷底、山脊、下坡、中坡、上坡和平坡。相比于SRTM，融合后DEM山脊、上坡、中坡、下坡和谷底誤差分別降低了0.40 m、0.79 m、0.99 m、0.39 m和1.32 m，平坡略微增加；相比于ASTER，融合后DEM精度均明顯得到提高，山脊、上坡、中坡、平坡、下坡和谷底誤差分別降低了6.1 m、2.74 m、1.43 m、1.74 m、3.04 m和1.29 m。

由圖6(d)可知，各高程誤差均隨地形起伏度增加而增加，最大可分別達到18.91 m、17.54 m和16.42 m；當地形起伏度大于20 m時，融合后DEM精度均高于SRTM、ASTER，說明地形起伏度對DEM高程精度的影響在融合之后得到降低。

從整體上看，融合后DEM精度最優，SRTM次之，ASTER最差；但在地形平坦地區，SRTM精度略高于融合后DEM。坡度較大地區往往對應地形起伏大的地區，所以坡度與地形起伏度對DEM精度影響類似。

3.3 實驗驗證

為了進一步驗證該網絡對其他不同地形特征區域具有遷移性，本文選取美國愛達荷州北部某區域為驗證區(圖7(a))。該區域東鄰蒙大拿州，處于密蘇里河流域，面積約為30 km2，高程范圍為1 291.65～2 022.57 m，經緯度范圍為114.74°W～114.65°W，46.56°N～46.62°N，平均坡度為20.7°。本文選擇將在https：//portal.opentopography.org/網站下載的1 m分辨率LiDAR(light detection and ranging)數據作為參考數據；然后，將已訓練的BPNN應用于驗證區SRTM和ASTER的融合，得到融合后DEM(圖7(b))；最后，以驗證區LiDAR數據隨機生成的1 000個點作為檢核點統計DEM高程誤差，并對融合前后的DEM進行精度分析。

圖7 驗證區數據

由表2可知，融合后DEM精度最高，其次是ASTER，最后是SRTM。相比于ASTER，融合后DEM平均絕對誤差、中誤差和標準差分別降低了1.14 m、1.23 m和0.75 m；相比于SRTM，融合后DEM精度分別提高了2.31 m、2.64 m和1.04 m。

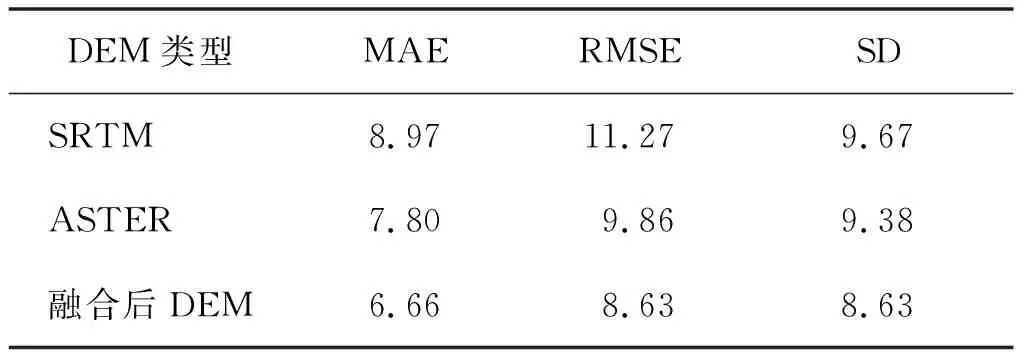
表2 不同DEM精度指標 m

為了探究驗證區各地形因子對DEM高程精度的影響，本文首先從SRTM中提取坡度、坡向、坡位和地形起伏度，并采用相同的方法分別將坡度劃分為五級、坡向劃分為四類、坡位分為六類，再將地形起伏度按0～15 m、15～45 m、45～60 m和60～68 m分為四類，以檢核點高程為標準，SRTM、ASTER和融合DEM數據各類型高程誤差標準差統計結果如圖8所示。

圖8 驗證區不同地形因子DEM誤差統計

由圖8可知，各地形因子對DEM高程精度的影響在融合之后均得到降低，特別是坡度和地形起伏度。SRTM、ASTER和融合后DEM各坡度等級誤差均隨坡度增大而增大，SRTM受坡度影響最大；融合后DEM各坡向類型高程誤差均低于ASTER，融合后DEM在NE、SE、NW精度均高于SRTM；在各坡位類型中，山脊和谷底高程誤差較大，平坡最小，融合后DEM精度均高于ASTER；地形起伏度對DEM精度影響與坡度類似。實驗結果表明，驗證區與研究區結果趨于一致，BPNN同樣適用于其他不同地形特征區域。

4 結束語

為了彌補SRTM和ASTER各自數據獲取技術的不足，本文提出了一種基于神經網絡預測模型的加權融合方法，實現了SRTM和ASTER數據的有效融合。以具有黃土高原典型地貌特征的董志塬區域為研究區、美國愛達荷州北部某區域為驗證區對該實驗方法進行驗證。結果分析表明：相比于原始的SRTM，研究區融合DEM中誤差降低了0.40 m，標準差降低了0.79 m；相比于原始的ASTER，融合后DEM得到顯著提高，中誤差和標準差分別降低了3.16 m和2.07 m；在各地形因子影響下，融合后DEM精度均是最優，各地形因子對DEM高程精度的影響在融合之后都得到降低。而驗證區與研究區結果趨于一致，表明本文提出的顧及地形因子的神經網絡方法具有可行性和有效性。

本文提出的神經網絡預測方法受地形因子類別和神經網絡模型影響，因此，后續將在實驗中添加更多有效的地形因子和替換網絡模型，增加網絡有效輸入數據，優化網絡結構，以獲取最有效的神經網絡預測模型。