基于MATLAB_GUI的矩陣相關(guān)運(yùn)算驗(yàn)證系統(tǒng)設(shè)計

聶奧洋 李軍成

摘要：矩陣的相關(guān)運(yùn)算是代數(shù)學(xué)中重要的內(nèi)容，在許多領(lǐng)域也有著廣泛的應(yīng)用。為了對矩陣相關(guān)運(yùn)算的結(jié)果進(jìn)行驗(yàn)證，基于MATLAB的圖形用戶界面（GUI）平臺設(shè)計了一個矩陣相關(guān)運(yùn)算的驗(yàn)證系統(tǒng)。該系統(tǒng)通過調(diào)用MATLAB自帶的有關(guān)函數(shù)進(jìn)行設(shè)計，主要包括矩陣的運(yùn)算、矩陣的求值、線性方程組求解等3個模塊。用戶只需根據(jù)提示信息輸入相應(yīng)的變量，系統(tǒng)即可快速給出矩陣相關(guān)運(yùn)算的結(jié)果，為矩陣相關(guān)運(yùn)算的驗(yàn)證提供了一個有效的平臺。

關(guān)鍵詞：MATLAB;圖形用戶界面;矩陣運(yùn)算;驗(yàn)證系統(tǒng)

中圖分類號：TP311 ? ? ? ?文獻(xiàn)標(biāo)識碼：A

文章編號：1009-3044（2021）30-0088-04

1 引言

MATLAB將數(shù)值分析、矩陣計算、科學(xué)數(shù)據(jù)可視化等強(qiáng)大功能聚集在一起，為工程設(shè)計、科學(xué)研究等涉及數(shù)值計算的領(lǐng)域提供了靈活便捷的解決方案。MATLAB在矩陣運(yùn)算以及線性方程組的求解中，擁有強(qiáng)大的計算功能，學(xué)生可以利用MATLAB高效地進(jìn)行基本的矩陣運(yùn)算[1]。

關(guān)于矩陣計算的GUI設(shè)計[2-4]有很多，但這些設(shè)計主要存在的問題有：1）界面不能用于矩陣的不同計算;2）界面設(shè)計過于復(fù)雜，不便使用。矩陣的理論和方法在數(shù)學(xué)和其他學(xué)科中都具有重要的意義，但許多學(xué)生無法克服矩陣龐大的計算量帶來的恐懼，從而喪失了學(xué)習(xí)的興趣和動力[5]。為此，本文對矩陣相關(guān)運(yùn)算進(jìn)行細(xì)化分類，通過MATLAB自帶的函數(shù)設(shè)計了一個矩陣相關(guān)運(yùn)算驗(yàn)證系統(tǒng)，為輔助教師的教學(xué)和學(xué)生的學(xué)習(xí)提供了便利。

2 系統(tǒng)的設(shè)計

2.1 系統(tǒng)主界面的設(shè)計

演示平臺總界面的設(shè)計思路是將矩陣的所有相關(guān)知識點(diǎn)分成了以下三類：矩陣的運(yùn)算、矩陣的求值、線性方程組求解，系統(tǒng)主界面的設(shè)計如圖1所示。

2.2 矩陣的運(yùn)算界面設(shè)計

2.2.1 矩陣的加法界面設(shè)計

矩陣的加法模塊的界面設(shè)計如圖2所示。該界面給出了和與差的定義以及運(yùn)算規(guī)則，包含兩個可編輯文本框，分別用來讀取用戶所輸入的矩陣，然后通過按鈕（計算A+B）和按鈕（計算A-B）得出用戶所需數(shù)值結(jié)果，結(jié)果會在按鈕下方的列表框中顯示。

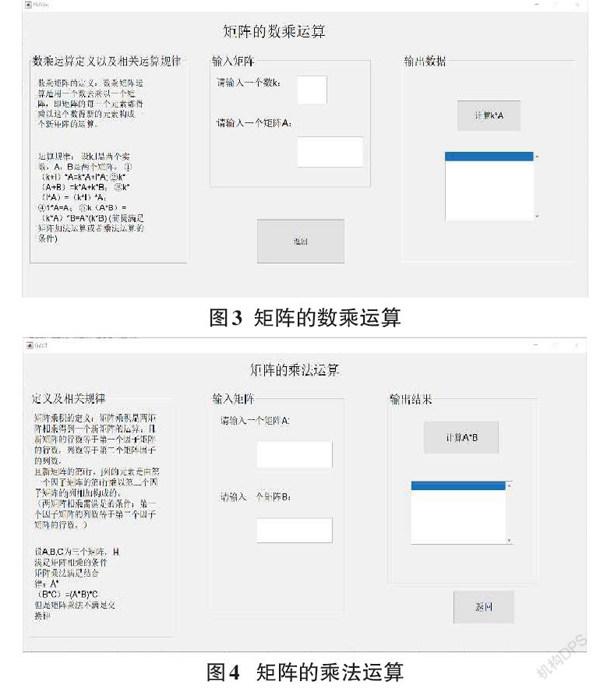
2.2.2 矩陣的數(shù)乘界面設(shè)計

矩陣的數(shù)乘模塊界面設(shè)計如圖3所示。該界面給出了一些矩陣與數(shù)相乘的運(yùn)算規(guī)律以及遵循的運(yùn)算法則，讓用戶在使用該界面時同時可以增加用戶對矩陣數(shù)乘知識的學(xué)習(xí)。該界面提供兩個可編輯文本框，一個用來獲取用戶所輸入的數(shù)k，另一個用來獲取用戶所需要計算的矩陣。

2.2.3 矩陣乘法的界面設(shè)計

矩陣乘法模塊的界面設(shè)計與圖4所示。跟矩陣的數(shù)乘運(yùn)算類似，該界面設(shè)置兩個可編輯文本框用于獲取用戶所輸入的矩陣，列表框用于反饋結(jié)果。用戶在可編輯框輸入需要計算的矩陣，點(diǎn)擊計算按鈕，界面系統(tǒng)會自動通過MATLAB所包含的函數(shù)對輸入矩陣進(jìn)行處理反饋結(jié)果。

2.2.4 矩陣求逆的界面設(shè)計

矩陣求逆模塊的界面設(shè)計如圖5所示。該界面給出了矩陣求逆的一些相關(guān)理論知識和編輯文本框、按鈕等操作按鍵。用戶通過對可編輯框的編輯，使MATLAB利用get函數(shù)獲取到所需要加工的矩陣，然后利用程序所指定的符號對矩陣進(jìn)行求逆，最后通過列表框反饋。

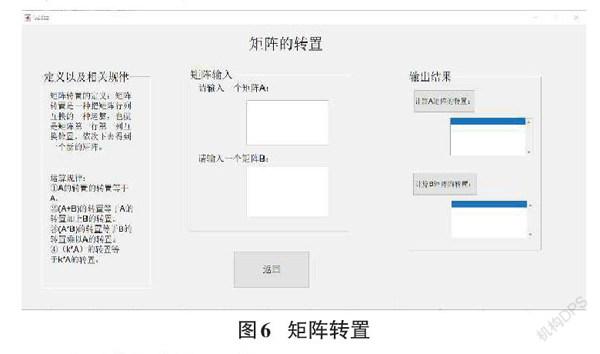
2.2.5 矩陣轉(zhuǎn)置的界面設(shè)計

矩陣轉(zhuǎn)置模塊的界面設(shè)計如圖6所示。該界面利用MATLAB轉(zhuǎn)置運(yùn)算符對用戶輸入的矩陣進(jìn)行加工，得出矩陣的轉(zhuǎn)置。在該界面的左邊主要給出的是矩陣轉(zhuǎn)置的相關(guān)知識點(diǎn)和轉(zhuǎn)置運(yùn)算的規(guī)律，方便用戶學(xué)習(xí)，中間部分設(shè)置兩個可編輯文本框提供給用戶輸入他們想處理的矩陣，模塊右邊是矩陣處理的按鈕以及處理過后結(jié)果的顯示。

2.2.6 矩陣共軛的界面設(shè)計

矩陣共軛模塊的界面設(shè)計如圖7所示。該界面相比于矩陣轉(zhuǎn)置模塊的設(shè)計區(qū)別在于矩陣共軛轉(zhuǎn)置研究的是復(fù)數(shù)矩陣。

2.3 矩陣的求值界面設(shè)計

2.3.1 矩陣行列式計算的界面設(shè)計

行列式是方陣的一個非常重要的指標(biāo)，其計算本身具有一定的復(fù)雜度[6]。矩陣行列式計算的界面設(shè)計如圖8所示。該界面左邊排版方陣行列式的運(yùn)算性質(zhì)，中間利用get函數(shù)設(shè)計交互框用于提取用戶所輸入的矩陣，右邊利用MATLAB中det函數(shù)對get到的矩陣進(jìn)行處理反饋數(shù)據(jù)，注意所輸入的矩陣必須為方陣不然會提示錯誤。

2.3.2 矩陣求秩的界面設(shè)計

矩陣的秩應(yīng)用性十分廣泛，尤其是在判定向量組的線性相關(guān)性、求解方程組的解的結(jié)構(gòu)以及判定矩陣行（列）空間的基和維數(shù)上的應(yīng)用更為常見[7]。矩陣求秩的界面設(shè)計如圖9所示，該界面主要利用MATLAB rank函數(shù)精確快速地得出矩陣的秩。

2.3.3 矩陣求跡的界面設(shè)計

矩陣的跡作為矩陣的一個重要數(shù)字特征，在數(shù)值計算、逼近論和統(tǒng)計估計等方面都有著較為廣泛的應(yīng)用[8]。矩陣求跡的界面設(shè)計如圖10所示，該界面的設(shè)計類似于矩陣行列式的模塊進(jìn)行設(shè)計，在界面給出有關(guān)矩陣求跡的相關(guān)知識點(diǎn)，利用MATLAB已知函數(shù)trace函數(shù)，對矩陣進(jìn)行加工并反饋結(jié)果。

2.3.4 矩陣特征值與特征向量計算的界面設(shè)計

特征值與特征向量的理論體系已經(jīng)基本成熟，并且在其他領(lǐng)域中得到了廣泛的應(yīng)用[9]。矩陣特征值與特征向量計算的界面設(shè)計如圖11所示，該界面給出了特征值和特征向量的相關(guān)知識點(diǎn)，主要通過eig函數(shù)幫助用戶快速計算矩陣的特征值與特征向量。

2.3.5矩陣計算范數(shù)的界面設(shè)計

矩陣計算范數(shù)的界面設(shè)計如圖12所示，該界面給出了范數(shù)的定義，用get函數(shù)設(shè)計了可編輯框用于讀取用戶輸入的矩陣，再針對輸入矩陣計算不同的范數(shù)結(jié)果。

2.3.6 矩陣條件數(shù)計算的界面設(shè)計

矩陣條件數(shù)計算的界面設(shè)計如圖13所示，該界面的設(shè)計與矩陣范數(shù)模塊的設(shè)計類似，給出了條件數(shù)的定義，用get函數(shù)設(shè)計了可編輯框用于讀取用戶輸入的矩陣，再針對輸入矩陣計算不同的條件數(shù)結(jié)果。

2.4 線性方程組求解的界面設(shè)計

求解線性方程組是代數(shù)學(xué)中重要的知識模塊，在網(wǎng)絡(luò)流模型，動物遷徙模型[10]求解中也具有廣泛應(yīng)用。線性方程組求解的界面設(shè)計如圖14所示，該界面主要是利用矩陣的性質(zhì)進(jìn)行線性方程組有無解的判定和求解，對于有解的線性方程組可以利用常數(shù)矩陣和系數(shù)矩陣求解出該方程的解。用戶首先輸入線性方程組的系數(shù)矩陣、增廣矩陣、未知數(shù)個數(shù)以及等式右邊的常數(shù)向量，然后點(diǎn)擊判定方程組是否有解，如果此方程組有解則可點(diǎn)擊求解得到此方程組的解。

3 結(jié)束語

本文將矩陣相關(guān)運(yùn)算具體分為矩陣的運(yùn)算、矩陣的求值、線性方程組求解等3個模塊，基于MATLAB_GUI設(shè)計與開發(fā)了一個矩陣相關(guān)運(yùn)算的驗(yàn)證系統(tǒng)。所設(shè)計的系統(tǒng)界面美觀，功能齊全，運(yùn)行穩(wěn)定。在進(jìn)行操作時，只需修改可編輯框參數(shù)，便可得到所需要的數(shù)據(jù)，通過該系統(tǒng)可以解決一些較復(fù)雜矩陣的計算。

參考文獻(xiàn)：

[1] 寇娜.MATLAB在線性代數(shù)理論教學(xué)中應(yīng)用的探索[J].教育教學(xué)論壇，2020（29）：306-307.

[2] 郝琳，馬長林.Matlab/GUI的AHP成對比較矩陣的檢驗(yàn)及修正[J].電腦開發(fā)與應(yīng)用，2014，27（9）：76-78.

[3] 楊鳳英， 廖莎. 基于Matlab GUI線性代數(shù)計算器的設(shè)計與開發(fā)[J]. 甘肅科技， 2019， 35（21）： 1-3.

[4] 崔秋珍.基于MATLAB的《線性代數(shù)實(shí)驗(yàn)課程》GUI平臺設(shè)計與實(shí)現(xiàn)[J].電腦知識與技術(shù)，2012，8（31）：7513-7515，7522.

[5] 楊亞輝.用Matlab深入學(xué)習(xí)和理解矩陣知識[J].現(xiàn)代電子技術(shù)，2007，30（6）：175-177.

[6] 胡康秀，楊揚(yáng)，丁云，等.3類典型的“矩陣和”的行列式計算及其應(yīng)用[J].江西科學(xué)，2020，38（5）：619-620.

[7] 謝毅，徐聰.矩陣的秩的三種常見的應(yīng)用[J].數(shù)學(xué)學(xué)習(xí)與研究，2020（9）：154，156.

[8] 宿曈.矩陣跡的性質(zhì)及其應(yīng)用[J].高師理科學(xué)刊，2018，38（10）：45-47.

[9] 張亞. 矩陣的特征值與特征向量及其應(yīng)用[J]. 科技經(jīng)濟(jì)導(dǎo)刊， 2018， 26（11）： 79-84.

[10] 王偉珠. 線性方程組應(yīng)用分析[J]. 現(xiàn)代商貿(mào)工業(yè)， 2016（36）： 168-169.

【通聯(lián)編輯：王力】

收稿日期：2021-03-22

基金項(xiàng)目：湖南省普通高等學(xué)校教學(xué)改革研究項(xiàng)目“基于學(xué)科競賽驅(qū)動培養(yǎng)地方院校數(shù)學(xué)類應(yīng)用型創(chuàng)新人才的研究與實(shí)踐”（湘教通[2018]436號No.732）;湖南人文科技學(xué)院MOOC/SPOC課程建設(shè)項(xiàng)目“MATLAB語言基礎(chǔ)”（校教通〔2018〕85號No. 21）

作者簡介：聶奧洋（2001—），男，湖南婁底人，本科生，主要研究方向?yàn)閿?shù)學(xué)建模及其應(yīng)用;通信作者：李軍成（1982—），男，湖北省漢川市人，教授，博士，主要研究方向?yàn)閹缀卧O(shè)計與計算、數(shù)學(xué)建模。