建筑結構化爆作用級數型荷載動力系數研究

劉 榕，耿少波，賀耀北,3

(1.湖南省交通規(guī)劃勘察設計院有限公司，長沙 410200；2.中北大學 土木工程學科部，太原 030051;3.湖南大學 土木工程學院，長沙 410082)

重要的建筑物一般需進行抗爆設計，爆炸荷載作為一種偶然作用，常分為核爆、化爆和物理爆炸三類。和平與發(fā)展仍為當今時代發(fā)展主題，且受世界范圍內核材料的嚴格管控，核爆發(fā)生概率很低。我國大量危險性化工企業(yè)、工礦企業(yè)逐步被城市包圍，遍布的燃氣管網、加油加氣站、儲油儲氣站及煙花爆炸儲運等重大爆炸危險源的大量增加，建筑結構遭受化爆作用發(fā)生災害現象呈上升趨勢，例如2019年江蘇鹽城化工廠爆炸事故造成嚴重后果。同時，受國際政治變化、民族沖突、恐怖襲擊等不穩(wěn)定社會影響，選擇建筑結構進行常規(guī)武器爆炸襲擊的可能性也在增加，例如2015年我國駐索馬里使館遭受炸彈襲擊受到國際社會強烈關注。

國外進行建筑結構抗爆設計研究較早，并形成了相關設計手冊或指南，例如美國的技術手冊TM5-1300《抗偶然爆炸結構設計手冊》[1]、TM5-855-1《常規(guī)武器防護設計原理》[2]、UFC 3-340-02[3]和加拿大的CSA/S850-12[4]。我國民用抗爆設計主要在人防工程領域，現已形成國標GB 50038—2005《人民防空地下室設計規(guī)范》[5]，軌道交通領域RFJ 02—2009《軌道交通工程人民防空設計規(guī)范》，北京市DB 11/994—2013《平戰(zhàn)結合人民防空工程設計規(guī)范》。2012年修訂的GB 50009—2012《建筑結構荷載規(guī)范》[6]中也新增了常規(guī)武器爆炸作用的計算方法及說明。爆炸荷載結構響應涉及流固耦合、幾何及材料非線性等計算內容，計算效率很低，不利于結構抗爆設計。因此，與國外抗爆設計規(guī)范類似，我國現行規(guī)范在結構抗常規(guī)武器等化爆作用設計時，建議采用動力系數進行等效靜力荷載換算，實現基于構件層次的結構抗爆設計。現行規(guī)范將爆炸荷載簡化為正超壓作用下等沖量線性衰減模式。動力系數需要由等效單自由體系彈塑性振動響應得出，該振動方程為二階常系數微分方程，荷載簡化后使得方程求解容易，因此該簡化模型得到了國內外規(guī)范廣泛認可。

在研究領域，Biggs[7]較早采用線性衰減荷載等效單自由度法對無阻尼簡支梁、固端梁、簡支-固端梁及雙向板等進行了等效靜載分析，并形成了動力系數的近似計算圖解法；楊科之等[8]采用線性衰減荷載等效單自由度法研究了動力系數與延性比的關系，指出了線性衰減荷載計算受限范圍；方秦等[9-10]研究了鋼筋混凝土梁結構在線性衰減爆炸作用下的彎曲、剪切及彎剪破壞模式，確定了線性衰減荷載作用下梁式構件剪力動力系數理論;Nagata等[11]提出了修正的等效單自由度模型，使等效單自由體系模型能夠適用于近場爆炸作用下梁的最大位移計算；師燕超等[12-14]采用可靠度理論分析爆炸荷載，考慮了梁式構件材料、尺寸的不確定性，更新了等效單自由度體系理論及動力系數求解的運用。

從化爆作用荷載參數測試來看，其衰減曲線采用指數型或級數型表達比較合適。線性衰減荷載在等沖量條件下保持超壓峰值不變，通過調低正超壓作用真實時長，來保證沖擊波的正沖量為實際數值，這種簡化使沖量、時間比增大，結構設計更保守一些。換言之，對于絕大多數民用建筑結構，可能會導致制造成本偏高。耿少波等[15-16]采用指數型爆炸荷載求解了無阻尼體系下梁式構件動力位移響應及等效靜載動力系數，對衰減曲線形狀系數對動力系數的影響缺少分析。Gantes等[17]采用軟件分析指數型爆炸作用無阻尼單自由度結構的彈塑性位移響應解，指出指數型函數在進行動力學方程求解時較為復雜，可采用其他曲線函數進行解答。

爆炸荷載作為建筑結構承受的一種偶然荷載，不同于其他常規(guī)荷載，受炸藥的嚴格管控，目前開展爆炸荷載下的結構試驗相對較少，且主要集中在建筑結構典型配筋率、特定截面形式或特殊材料開展[18-19]。因此，加強曲線型衰減爆炸荷載結構響應理論分析成為完善抗爆設計理論的一項重要基礎工作。基于彈性的抗爆設計理論簡便但會導致制造成本過高，若允許結構進入一定的塑性階段或形成特定塑性鉸，將會降低等效靜載動力系數，進而降低抗爆設計工程造價，因此，國內外規(guī)范廣泛采用考慮延性比的彈塑性進行抗爆設計。結構塑性階段振動響應與荷載作用時長密切相關，等沖量線性衰減荷載作用時長小于爆炸荷載真實作用時長，這種等效處理方式，必然對等效靜載動力系數產生影響；而且不同當量炸藥、不同比例距離產生的爆炸荷載衰減曲線波形系數不同，這些參數對動力系數影響如何，國內外鮮有研究。

作者選用能充分反映爆炸荷載曲線衰減形式的級數型數學函數完成動力系數與延性比的計算公式推導，并與現行建筑結構規(guī)范、人防工程規(guī)范推薦使用的等沖量線性衰減荷載下的動力系數進行對比，進一步考查簡化荷載所帶來的計算誤差。

1 抗爆結構振動微分方程

1.1 爆炸荷載等效單自由度振動方程

根據動力學理論可知，忽略阻尼后的抗爆結構彈性階段動力學方程為

(1)

式中：Me為等效單自由度體系中等效質量；Ke為等效剛度；Pe(t)為等效荷載；W(t)為觀察截面位置結構動位移；t為結構振動的時間變量。

Me=mlkM，Pe(t)=Δp(t)lkL，Ke=KkL

(2)

式中：m為結構單位長度質量；l為結構跨度；kM、kL分別為彈性階段荷載質量、荷載轉換系數；K為結構剛度。進一步定義kML=kM/kL,則式(1)變?yōu)?/p>

(3)

同理，忽略塑性階段動力學方程可寫為

(4)

式中：kml為塑性階段等效質量與等效荷載比；qm=KWT/l,WT為彈性階段最大位移。

從耿少波等的研究可知若采用指數型函數描述曲線爆炸荷載超壓函數時為

(5)

式中：Δpm為超壓峰值；f(t)為歸一化后的超壓衰減函數；t+為正超壓沖擊波作用時長；a為指數型衰減荷載曲線系數。

由圖1及函數理論可知，級數型爆炸荷載無法直接確定級數的組成項、組合系數，需先構建冪函數進行冪級數的確定，再進一步確定級數型荷載的函數表達式。其中冪函數描述爆炸荷載超壓函數時為

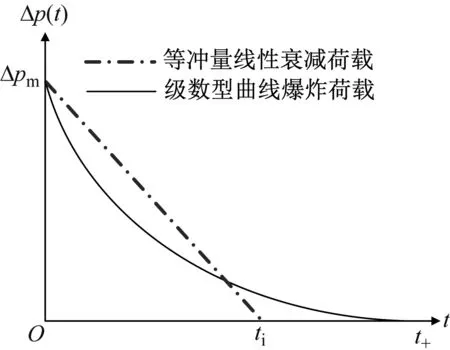
圖1 爆炸荷載時長關系圖Fig.1 Load duration diagram for different blast loadings

(6)

式中,n為冪函數的次冪。

采用指數型函數作為等沖量基準時，將式(5)在其作用時長內積分后，沖量為

i=Δpmt+[1/a+(e-a-1)/a2]

(7)

同理，可確定等沖量作用下冪函數的次冪為

(8)

分析式(5)可知，曲線波形系數a越大，t+以后的超壓函數數值越接近0。結合文獻中實測數據，參數a在1～2能充分反映負超壓段，本文選用此范圍進行分析，此時對應參數n范圍為1.72～2.52。n為非自然數時，式(3)及式(4)無解。由此時n最接近的自然數為1與3。若將冪函數型用級數型代替，則有

Δp(t)=Δpmf(t)=

(9)

或

Δp(t)=Δpmf(t)=

(10)

式中,b0、b1為級數型爆炸荷載組合系數。

由杜哈梅積分可知，式(3)對應彈性階段位移解、速度解為

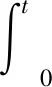
(11)

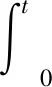
(12)

式中：Wst為Δpm為靜載時的靜位移；ω為結構振動頻率；τ為積分時間參數。

若定義tT為彈性結束時刻，則此時刻位移及對應的速度為

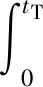
(13)

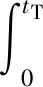
(14)

由式(3)及式(13)、式(14)可知，塑性階段結構振動位移及速度為

W(t)=WT+vT(t-tT)+

(15)

(16)

基于理想彈塑性理論的等效靜載動力系數為

(17)

1.2 級數型爆炸荷載參數確定

由圖1可知，等沖量線性衰減荷載的等效時長為ti，指數型或級數型爆炸荷載的真實作用時長均為t+。以指數型爆炸荷載為基準，根據等沖量線性衰減荷載函數

(18)

將其積分后利用與式(7)的相等條件，可計算出兩種荷載作用時長關系

(19)

根據式(9)，一三次項級數型荷載沖量為

i=Δpmt+(b0/2+b1/4)

(20)

由式(10)，二三次項級數型荷載沖量為

i=Δpmt+(b0/3+b1/4)

(21)

由與指數型沖量相等、超壓峰值相等兩條件，可分別求出一三次、二三次項級數的組合參數為

b1=2-4/a-4(e-a-1)/a2，b0=1-b1

(22)

b1=4-12/a-12(e-a-1)/a2，b0=1-b1

(23)

2 基于延性比的動力系數理論解

2.1 第一種塑性狀態(tài)

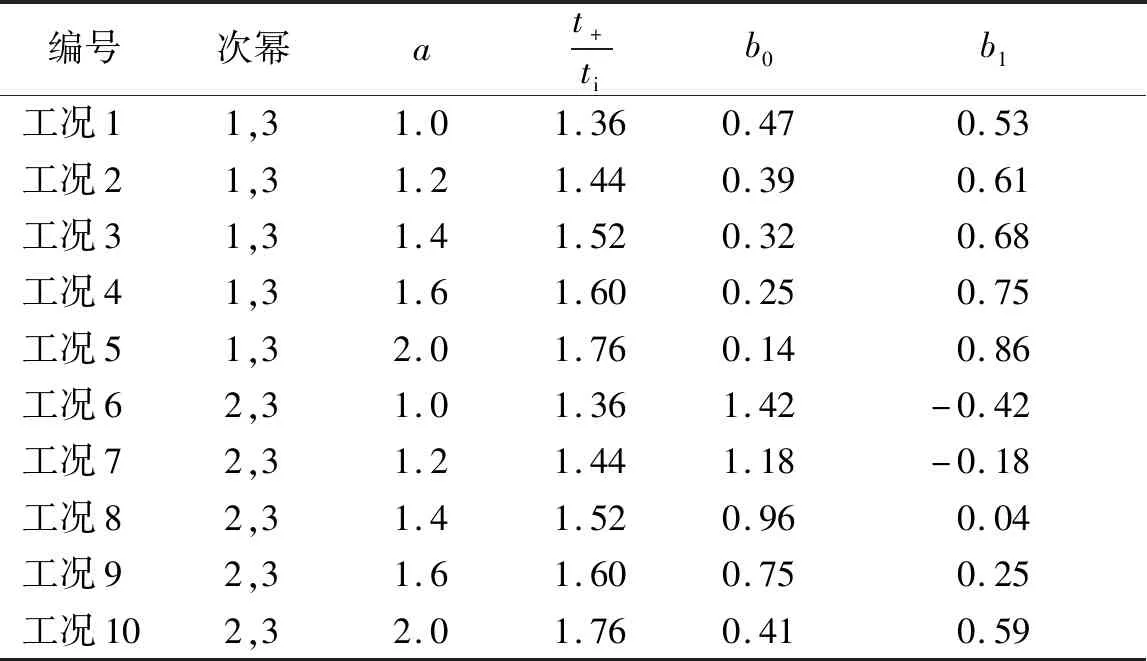
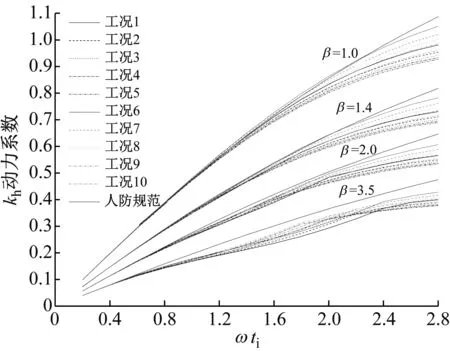
爆炸荷載真實作用時長t+或等沖量線性衰減荷載等效時長ti數值很小，可認為低于結構彈塑性振動最大位移時間tm。結構完成彈性振動進入塑性的時刻tT存在兩種形式：第一種塑性狀態(tài)，t+(或ti)

令θT=ωtT、θ+=ωt+，對于第一種塑性狀態(tài)，將式(9)、式(13)代入式(17)，可得一三次級數型爆炸荷載動力系數為

(24)

同理可得二三次級數型爆炸荷載動力系數為

(24)

由式(13)、式(14)可得一三次項級數型荷載作用，結構即將進入塑性時彈性振動速度與位移比

(25)

同理，二三次項級數型荷載作用下，結構即將進入塑性時彈性振動速度與位移比

(26)

由式(16)及塑性振動結束時速度為0可知

(27)

由式(15)可知

(28)

由延性比β定義及式(27)、式(28)可知，

(29)

從式(29)可以看出，當tT=tm時，即認為結構只有彈性振動無塑性階段時，結構延性比為1，此時為基于彈性理論的動力系數。

同時由等效單自由度體系參數可知

(30)

式中：Wst為超壓峰值視作靜載數值時結構靜位移；ω為結構振動頻率，計算公式為ω2=Ke/Me。

若采用式(25)及式(27)、式(30)代入式(29)后，可得一三次項級數型荷載在第一種塑性狀態(tài)下，基于動力系數的延性比

(31)

同理，可得二三次項級數型荷載在第一種塑性狀態(tài)下，基于動力系數的延性比

(32)

因此，根據結構設計所需延性比，結構振動頻率、級數型爆炸荷載組合參數、荷載作用時長等參數，即可由式(31)、式(32)進行迭代求出對應的動力系數。

2.2 第二種塑性狀態(tài)

由2.1節(jié)第二種塑性狀態(tài)定義，將式(9)、式(13)代入式(17)，可得一三次級數型爆炸荷載動力系數為

(33)

同理可得二三次級數型爆炸荷載動力系數為

(34)

由式(13)、式(14)可得一三次項級數型荷載作用，結構即將進入塑性時彈性振動速度與位移比

(35)

同理，二三次項級數型荷載作用下，結構即將進入塑性時彈性振動速度與位移比

(36)

由式(9)、式(16)及塑性振動結束時速度為0可知，一三次項級數型荷載作用下，進入塑性振動時速度為

(37)

將其代入式(30)后可得

(38)

同理，可得二三次項級數型荷載作用下，進入塑性時振動時速度與位移比

(39)

進一步令θm=ωtm，且令式(36)與式(38)相等時，便可得一三次項級數型荷載作用下表達式

(40)

同理，二三次項級數型荷載作用下表達式為

(41)

由式(15)及延性比定義，經過積分后，對于一三次項級數型荷載作用，其表達式為

(42)

同理，對于二三次項級數型荷載作用，延性比為

(43)

由第二種塑性狀態(tài)延性比式(42)、式(43)可知，比第一種塑性狀態(tài)對應的延性比式(31)、式(32)中多一參數θm，此參數不來源于爆炸荷載或結構設計參數，需由式(40)或式(41)求出。

3 算例驗證

3.1 算例工況

GB 50009—2012《建筑結構荷載規(guī)范》指出等沖量線性衰減荷載超壓峰值、等效時長來源于GB 50038—2005《人民防空地下室設計規(guī)范》；未明確給出動力系數計算公式。因此，以GB 50038—2005《人民防空地下室設計規(guī)范》中動力系數計算公式為本文對比基準，完成本文計算工況驗證。

彈性及塑性階段等效質量與等效荷載比kML、kml，由GB 50038—2005《人民防空地下室設計規(guī)范》分別取值0.78、0.66；延性比β由GB 50038—2005《人民防空地下室設計規(guī)范》中規(guī)定的1～4選擇典型數據進行；等沖量線性衰減荷載作用下θi由楊科之等、耿少波等的研究中確定的典型數據0.2～2.8進行；爆炸荷載曲線衰減波形系數a由Gantes等研究中的數值表征的典型范圍1～2進行。由上述確定的參數數值，進一步形成一三次項、二三次項級數型荷載作用下計算工況，共10種計算工況，如表1所示。

表1 爆炸荷載算例工況Tab.1 Calculation situations for blast loading

完成各種計算工況及對應的規(guī)范公式計算后，結果如圖2所示。

3.2 結果分析

一三次、二三次項級數型爆炸荷載動力系數曲線均能在兩種塑性狀態(tài)下光滑過渡。在固定的荷載結構參數θi(即ωti)數值下，隨著波形系數a的增加，荷載真實作用時長與線性荷載等效時長比值增大，級數型爆炸荷載動力系數也與規(guī)范公式計算動力系數差值逐漸增大。所有的計算工況在相同的延性比β作用下，動力系數Kh隨θi增大而增大。爆炸荷載及其作用時長ti無法控制降低，有效地降低結構參數ω是一種可行方式。

(a)第一組延性比

等沖量、等峰值、等作用時長條件下，二三次項級數型較一三次項級數型爆炸荷載接近規(guī)范公式的動力系數計算結果。當β<2.5且θi<1.2時，可忽略兩種級數型荷載動力系數之間差異，與規(guī)范線性衰減荷載動力系數最大誤差在2%以內，即結構為“密閉、防水要求高”的使用要求時，對于常規(guī)武器等化爆作用，可忽略荷載曲線類型，直接采用規(guī)范推薦公式；當β<2.5且θi≥1.2時，工況6為所有工況中動力系數最大數值，與規(guī)范計算結果差值最小為8.2%，工況5為所有工況中動力系數最小數值，與規(guī)范計算結果差值最小為19.8%，此時采用一三次項級數型爆炸荷載是降低造價的一種良好選擇；當β≥2.5且θi<1.2時，可忽略級數型爆炸荷載的次項組合情況，選用任何一種級數型爆炸荷載均會降低造價；當β≥2.5且θi≥1.2時，動力系數與級數型爆炸荷載組合次項、波形系數a均發(fā)生關聯(lián)，a=1.0的二三次項級數型爆炸荷載對應的工況6，與規(guī)范公式差異最小為10.1%，a=2.0的一三次項級數型爆炸荷載對應的工況1，與規(guī)范公式差異最大為37.2%，此時參數θi為1.8。

4 結 論

(1)本文推導完成的化爆作用級數型爆炸荷載模式下動力系數公式，采用真實荷載作用時長的曲線型函數，劃分了兩種塑性狀態(tài)，比現行規(guī)范線性衰減函數下的爆炸荷載動力系數精準。

(2)級數型爆炸荷載動力系數與曲線波形系數a、項數組合系數b0、b1、結構荷載參數θ+等有關，整體上級數型爆炸荷載動力系數均小于規(guī)范計算結果，二三次項級數型較一三次項級數型爆炸荷載動力系數接近規(guī)范。

(3)當延性比β<2.5且結構荷載參數θi<1.2時，級數型與線性爆炸荷載模式差異可忽略，可采用人防設計規(guī)范提供的簡化動力系數公式進行抗爆設計。

(4)當β<2.5且θi≥1.2時，一三次項級數型爆炸荷載動力系數較低，可降低造價；當β≥2.5且θi<1.2時，可忽略級數型爆炸荷載的次項組合情況，選用任何一種級數型爆炸荷載的動力系數均可降低造價；當β≥2.5且θi≥1.2時，若采用較低的動力系數，需考慮級數型次項組合、曲線波形系數a因素后確定。