改進(jìn)的強(qiáng)追蹤平方根無(wú)跡卡爾曼濾波時(shí)變結(jié)構(gòu)參數(shù)識(shí)別

楊紀(jì)鵬，夏 燁，閆業(yè)祥，孫利民,2

(1.同濟(jì)大學(xué) 土木工程學(xué)院，上海 200092;2.同濟(jì)大學(xué) 土木工程防災(zāi)國(guó)家重點(diǎn)實(shí)驗(yàn)室，上海 200092)

土木工程結(jié)構(gòu)在強(qiáng)地震荷載作用下由于結(jié)構(gòu)損傷而引起系統(tǒng)參數(shù)突變，其包括結(jié)構(gòu)剛度、阻尼以及描述系統(tǒng)行為的其他參數(shù)，因而考慮參數(shù)時(shí)變特性的結(jié)構(gòu)系統(tǒng)識(shí)別得到越來(lái)越多的重視。

Yang等[1]提出自適應(yīng)最小二乘法，該方法在識(shí)別結(jié)構(gòu)參數(shù)時(shí)需要觀測(cè)結(jié)構(gòu)的位移、速度和加速度，實(shí)際中地震作用下結(jié)構(gòu)的位移和速度是很難觀測(cè)到的，而加速度是容易測(cè)得的物理量。

Yang等[2-3]提出自適應(yīng)擴(kuò)展卡爾曼濾波法，該方法基于擴(kuò)展卡爾曼濾波法(extended Kalman filter，EKF)，在狀態(tài)誤差協(xié)方差矩陣中引入自適應(yīng)矩陣，追蹤突變結(jié)構(gòu)參數(shù)。擴(kuò)展卡爾曼濾波是用泰勒展開(kāi)式去線性近似狀態(tài)估計(jì)值和量測(cè)觀測(cè)值。該理念處理非線性模型的思想清晰，濾波過(guò)程簡(jiǎn)單有效；但該方法也有明顯的缺陷：①進(jìn)行泰勒級(jí)數(shù)近似展開(kāi)時(shí)需要計(jì)算雅克比矩陣(Jacobian)，但對(duì)于有些非線性系統(tǒng)，其Jacobian矩陣不易計(jì)算；②通常EKF僅保留一階精度，若要提高到二階精度則要計(jì)算海塞矩陣，計(jì)算過(guò)程更加復(fù)雜；③因僅保留一階精度，通常需要較高的采樣頻率才能保證濾波效果。

雷鷹等[4]將靜力凝聚法與擴(kuò)展卡爾曼濾波法相結(jié)合，識(shí)別結(jié)構(gòu)參數(shù)，同時(shí)定量識(shí)別結(jié)構(gòu)節(jié)點(diǎn)損傷程度，該方法基于擴(kuò)展卡爾曼濾波，對(duì)于復(fù)雜系統(tǒng)求解Jacobian矩陣比較困難。

Julier等[5]根據(jù)確定性采樣提出的無(wú)跡卡爾曼濾波(unscented Kalman filter，UKF)以Unscented變換來(lái)近似計(jì)算系統(tǒng)狀態(tài)的后驗(yàn)均值和協(xié)方差，相較于直接近似非線性函數(shù)本身，前者更容易實(shí)現(xiàn)，UKF能以至少二階精度逼近任何非線性系統(tǒng)。但傳統(tǒng)UKF存在協(xié)方差矩陣開(kāi)方時(shí)矩陣奇異的數(shù)學(xué)問(wèn)題。謝強(qiáng)等[6-7]提出奇異值分解(singular value decomposition,SVD)計(jì)算狀態(tài)誤差協(xié)方差矩陣的平方根，但效果欠佳。

池傳國(guó)等[8]提出一種基于M估計(jì)的強(qiáng)跟蹤SVD-UKF算法。該算法利用M估計(jì)理論，對(duì)異常新息數(shù)據(jù)進(jìn)行“篩選”，保留有用新息，剔除有害新息，有效避免由衛(wèi)星信號(hào)野值引起的粗差對(duì)強(qiáng)跟蹤SVD-UKF算法的魯棒性影響。

王小旭等[9-10]提出強(qiáng)追蹤無(wú)跡卡爾曼濾波器，該方法克服了傳統(tǒng)UKF無(wú)法追蹤時(shí)變結(jié)構(gòu)參數(shù)的缺點(diǎn)，但其計(jì)算過(guò)程中需要計(jì)算狀態(tài)預(yù)測(cè)誤差協(xié)方差矩陣的平方根，其數(shù)值穩(wěn)定性較差。

Van der Merwe等[11]提出平方根卡爾曼濾波，該方法基于UKF的算法框架，以協(xié)方差矩陣的平方根代替協(xié)方差矩陣進(jìn)行遞推運(yùn)算。該算法避免了時(shí)間狀態(tài)預(yù)測(cè)時(shí)協(xié)方差矩陣開(kāi)方計(jì)算，但在濾波結(jié)果更新協(xié)方差矩陣平方根時(shí)，需要進(jìn)行喬里斯基分解一階更新，其對(duì)矩陣的正定性的要求與UKF一樣高，并沒(méi)有從根本上解決數(shù)值計(jì)算時(shí)不穩(wěn)定的問(wèn)題。

張玉峰等[12]基于平方根濾波的思想，對(duì)傳統(tǒng)的Sage-Husa自適應(yīng)濾波算法進(jìn)行了改進(jìn)，并與平方根無(wú)跡卡爾曼濾波(square root unscented Kalman filter,SRUKF)結(jié)合，該算法能直接對(duì)非線性系統(tǒng)的狀態(tài)方差矩陣和噪聲方差矩陣的平方根進(jìn)行遞推與估算，確保狀態(tài)和噪聲方差矩陣的對(duì)稱性和非負(fù)定性，但文中仍需計(jì)算量測(cè)矩陣的Jacobian矩陣，未引入強(qiáng)追蹤濾波因子，不能有效追蹤時(shí)變系統(tǒng)參數(shù)。

葉浩澤等[13]在標(biāo)準(zhǔn)的平方根UKF算法上，首先改用了球型無(wú)跡變換對(duì)權(quán)系數(shù)以及Sigma點(diǎn)進(jìn)行計(jì)算選取；其次改進(jìn)了SRUKF中平方根矩陣的分解方法；同時(shí)在預(yù)測(cè)誤差協(xié)方差矩陣中引入了自適應(yīng)衰減因子。該文中也需計(jì)算觀測(cè)矩陣的Jacobian矩陣，且文中計(jì)算強(qiáng)追蹤濾波因子的方法并不適用于土木結(jié)構(gòu)系統(tǒng)參數(shù)識(shí)別。

李敏等[14]提出一種改進(jìn)的強(qiáng)跟蹤平方根無(wú)跡卡爾曼濾波(strong tracking square root unscented Kalman filter，STSRUKF)導(dǎo)航方法，采用一種改進(jìn)的平方根分解方法，改善了濾波器的穩(wěn)定性。同時(shí)，基于強(qiáng)跟蹤濾波器理論，引入多重自適應(yīng)衰減因子調(diào)節(jié)協(xié)方差矩陣，使得濾波器具有強(qiáng)跟蹤能力。數(shù)值模擬表明該方法效果并不好，同時(shí)該方法需要計(jì)算量測(cè)矩陣的Jacobian矩陣，文中所使用的強(qiáng)追蹤濾波因子算法也不適用于土木結(jié)構(gòu)系統(tǒng)參數(shù)識(shí)別。

基于以上問(wèn)題，本文提出改進(jìn)的強(qiáng)追蹤平方根無(wú)跡卡爾曼濾波方法(modified strong tracing square root unscented Kalman filter ，MSTSRUKF)。該方法首先改進(jìn)了協(xié)方差矩陣平方根計(jì)算方法，根據(jù)協(xié)方差定義直接使用QR分解計(jì)算其平方根，避免使用喬里斯基分解一階更新，使協(xié)方差矩陣平方根計(jì)算過(guò)程無(wú)條件數(shù)值穩(wěn)定；其次，引入量測(cè)矩陣Jacobian矩陣的等價(jià)形式進(jìn)行計(jì)算，對(duì)于非線性量測(cè)系統(tǒng)，可避免求解Jacobian矩陣，減小計(jì)算工作量，使該方法更具有普適性；最后，引入強(qiáng)追蹤濾波因子，根據(jù)土木工程結(jié)構(gòu)參數(shù)特點(diǎn)，調(diào)整濾波因子矩陣對(duì)應(yīng)項(xiàng)的比值，使該方法在引起較小參數(shù)波動(dòng)的情況下即可識(shí)別到時(shí)變結(jié)構(gòu)參數(shù)。

1 改進(jìn)的平方根強(qiáng)追蹤無(wú)跡卡爾曼濾波

1.1 標(biāo)準(zhǔn)的SRUKF算法

考慮如下的離散非線性系統(tǒng)模型

(1)

式中：f(·)為非線性狀態(tài)函數(shù)；h(·)為非線性量測(cè)函數(shù)；Xk+1為n維系統(tǒng)狀態(tài)向量；Zk+1為m維量測(cè)向量；uk為s維系統(tǒng)輸入向量；wk為n維系統(tǒng)過(guò)程噪聲;vk+1為m維量測(cè)噪聲;wk和vk+1均為互不相關(guān)的零均值高斯白噪聲。且有

E(wk)=0,cov(wk,wj)=Qkδkj,

E(vk)=0,cov(vk,vj)=Rkδkj,

cov(wk,vj)=0

(2)

式中：Qk和Rk分別為系統(tǒng)過(guò)程噪聲協(xié)方差矩陣和系統(tǒng)量測(cè)噪聲協(xié)方差矩陣;δkj為kronecker函數(shù)。基于UKF的平方根無(wú)跡卡爾曼濾波(SRUKF)標(biāo)準(zhǔn)流程如下。

步驟1初始化狀態(tài)X0，狀態(tài)誤差協(xié)方差矩陣平方根S0

(3)

(4)

(5)

步驟3時(shí)間預(yù)測(cè)更新

(6)

(7)

(8)

(9)

步驟4量測(cè)更新

(10)

(11)

(12)

(13)

(14)

步驟5濾波結(jié)果更新

(15)

(16)

U=KkSZ

(17)

Sk+1|k+1=cholupdate{Sk+1|k,U,-1}

(18)

上述計(jì)算過(guò)程中用到的權(quán)值參數(shù)計(jì)算如下

(19)

式中:λ=α2(n+κ)-n;α為決定Sigma點(diǎn)在先驗(yàn)均值附近擴(kuò)展程度的主要尺度因子，通常取1×10-3<α≤1;β為第二個(gè)尺度因子，用于強(qiáng)調(diào)后驗(yàn)協(xié)方差計(jì)算的第0個(gè)Sigma點(diǎn)的權(quán)重;κ為三級(jí)比例因子，通常取κ=3-n;n為狀態(tài)向量的維數(shù);qr(·)為QR分解;cholupdate(·)為喬里斯基分解一階更新;上標(biāo)T為矩陣的轉(zhuǎn)置。

1.2 改進(jìn)的SRUKF算法

1.2.1 改進(jìn)的時(shí)間預(yù)測(cè)狀態(tài)向量誤差協(xié)方差矩陣平方根計(jì)算

在標(biāo)準(zhǔn)的SRUKF算法中，由式(8)與式(9)計(jì)算狀態(tài)向量時(shí)間預(yù)測(cè)的誤差協(xié)方差矩陣的平方根，即式(9)可等價(jià)描述為

(20)

式(9)通過(guò)cholupdate計(jì)算Sk+1|k時(shí)，要求式(20)等式右邊必須是正定的，其要求與標(biāo)準(zhǔn)的UKF中計(jì)算誤差協(xié)方差矩陣平方根一樣嚴(yán)格，實(shí)際運(yùn)算中由于舍入誤差的影響，很難保證矩陣的正定性，為此根據(jù)時(shí)間預(yù)測(cè)誤差協(xié)方差矩陣的定義

(21)

Sk+1|k=rT

(22)

又由式(21)推導(dǎo)得到

(23)

(24)

(25)

數(shù)值分析結(jié)果表明，式(25)對(duì)計(jì)算結(jié)果影響不大。

而李敏等提出如下的時(shí)間預(yù)測(cè)誤差協(xié)方差矩陣的計(jì)算方法

(26)

(27)

數(shù)值分析結(jié)果表明，式(26)、式(27)所提出的協(xié)方差計(jì)算方法參數(shù)識(shí)別結(jié)果并不理想。故本文提出如下協(xié)方差矩陣平方根計(jì)算方法

(28)

再通過(guò)式(24)計(jì)算Sk+1|k。

1.2.2 改進(jìn)的量測(cè)誤差協(xié)方差平方根計(jì)算

同理，式(12)、式(13)可改進(jìn)為

(29)

(30)

1.2.3 改進(jìn)的濾波更新協(xié)方差矩陣計(jì)算

計(jì)算濾波結(jié)果更新?tīng)顟B(tài)向量誤差協(xié)方差矩陣平方根時(shí)，式(17)、式(18)可等價(jià)描述為

(31)

這要求式(31)等式右邊必須是正定的，由于舍入誤差的影響，很容易使該部分失去正定性，因此還需對(duì)狀態(tài)估計(jì)誤差協(xié)方差矩陣平方根的計(jì)算做如下改進(jìn)。

根據(jù)狀態(tài)估計(jì)誤差協(xié)方差的定義

(32)

將式(16)代入式(32)得

(33)

同時(shí)，式(1)中的量測(cè)方程可寫為

Zk+1=Hk+1Xk+1+Vk+1

(34)

(35)

將式(34)、式(35)代入式(33)可得

(36)

式中，I為單位矩陣。

由于Vk+1與其他向量不相關(guān)，根據(jù)協(xié)方差矩陣定義，由式(36)可推導(dǎo)得到

(37)

根據(jù)狀態(tài)向量時(shí)間預(yù)測(cè)誤差協(xié)方差矩陣平方根計(jì)算的改進(jìn)方法，可得到改進(jìn)的濾波更新?tīng)顟B(tài)估計(jì)協(xié)方差矩陣的平方根計(jì)算方法

(38)

(39)

1.2.4 量測(cè)矩陣的改進(jìn)

對(duì)于復(fù)雜的非線性結(jié)構(gòu)，若觀測(cè)向量與狀態(tài)向量之間為非線性關(guān)系，為避免計(jì)算Jacobian矩陣，可使用量測(cè)矩陣Hk+1的等價(jià)形式。根據(jù)定義，狀態(tài)預(yù)測(cè)自協(xié)方差矩陣Pk+1|k，輸出預(yù)測(cè)自協(xié)方差矩陣PZZ,k+1和輸出預(yù)測(cè)互協(xié)方差矩陣PXZ,k+1可寫為式(40)～式(42)的形式

(40)

則可求得量測(cè)矩陣的等價(jià)形式為

(43)

1.3 強(qiáng)追蹤濾波算法

要使濾波器式(16)成為強(qiáng)追蹤濾波器的一個(gè)充分條件是實(shí)時(shí)在線調(diào)整增益矩陣Kk，使得

(44)

(45)

(46)

(47)

(48)

(49)

(50)

式中:tr[·]為矩陣的跡；l≥1為弱化因子；Γk+1為實(shí)際輸出殘差序列，可以表示為

(51)

設(shè)引入強(qiáng)追蹤漸消因子后的時(shí)間預(yù)測(cè)誤差協(xié)方差矩陣的平方根表示為Sk+1|k,new，計(jì)算出強(qiáng)追蹤濾波因子后，式(28)、式(24)表示的時(shí)間預(yù)測(cè)誤差協(xié)方差矩陣的平方根計(jì)算方法可更新為

(52)

(53)

根據(jù)以上推導(dǎo)，MSTSRUKF算法步驟可以描述為

步驟1根據(jù)式(3)、式(4)初始化系統(tǒng)狀態(tài);

步驟3時(shí)間預(yù)測(cè)更新，根據(jù)式(6)、式(7)、式(28)、式(24)計(jì)算時(shí)間預(yù)測(cè)狀態(tài)向量及協(xié)方差矩陣的平方根;

步驟4量測(cè)更新，根據(jù)式(10)、式(11)、式(29)、式(30)、式(14)計(jì)算量測(cè)更新

步驟5計(jì)算漸消因子矩陣，更新時(shí)間預(yù)測(cè)誤差協(xié)方差矩陣的平方根；根據(jù)式(43)計(jì)算量測(cè)矩陣Jacobian矩陣等價(jià)形式，根據(jù)式(46)～式(51)計(jì)算漸消因子矩陣，根據(jù)式(52)、式(53)計(jì)算引入漸消因子后的時(shí)間預(yù)測(cè)誤差協(xié)方差矩陣的平方根;

步驟6濾波更新,根據(jù)式(15)計(jì)算增益矩陣，根據(jù)式(16)計(jì)算k+1時(shí)刻狀態(tài)后驗(yàn)估計(jì)值；引入漸消因子后，k+1時(shí)刻狀態(tài)預(yù)測(cè)協(xié)方差矩陣根據(jù)式(54)～式(56)計(jì)算

(54)

(55)

(56)

2 數(shù)值算例驗(yàn)證

2.1 三自由度線性結(jié)構(gòu)系統(tǒng)

首先考慮一個(gè)三自由度線性結(jié)構(gòu)系統(tǒng)遭受地震激勵(lì)，其運(yùn)動(dòng)方程可以寫為

(57)

本算例中，取m1=m2=m3=1 000 kg，k1=120 kN/m，k2=120 kN/m，k3=60 kN/m。c1=c2=c3=0.6 kN·s/m，地震激勵(lì)選取El Centro地震波，采樣頻率100 Hz，地震持續(xù)時(shí)間31.2 s。

為模擬實(shí)際觀測(cè)中噪聲的干擾，在模擬的量測(cè)加速度數(shù)據(jù)中加入5%RMS(root mean square)的高斯白噪聲，然后使用低通濾波去除加速度時(shí)程中的高頻成分，濾波截?cái)囝l率為20 Hz，為了驗(yàn)證MSTSRUKF在識(shí)別線性結(jié)構(gòu)參數(shù)突變時(shí)的有效性，設(shè)定當(dāng)t=10 s時(shí):結(jié)構(gòu)一層剛度由k1=120 kN/m突變到k1=80 kN/m，二層剛度k2=120 kN/m突變到k2=80 kN/m，三層剛度k3=60 kN/m突變到k3=40 kN/m；結(jié)構(gòu)一層阻尼由c1=0.6 kN·s/m突變到c1=0.7 kN·s/m，二層阻尼c2=0.6 kN·s/m突變到c2=0.65 kN·s/m，三層阻尼c3=0.6 kN·s/m突變到c3=0.65 kN·s/m。狀態(tài)向量初值取為X0=[0,0,0,0,0,0,90,90,50,0.3,0.3,0.3]T

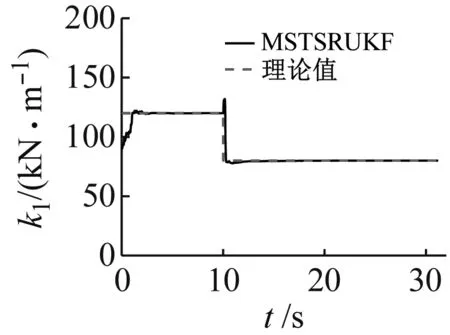
結(jié)構(gòu)參數(shù)識(shí)別結(jié)果,如圖1所示。結(jié)構(gòu)各層位移識(shí)別結(jié)果,如圖2所示。

若以1～10 s為第一階段，10.0～31.2 s為第二階段，不同階段參數(shù)最終識(shí)別結(jié)果如表1所示。

由圖1、圖2及表1可以看出，本文提出的MSTSRUKF：①能夠快速有效地識(shí)別突變的結(jié)構(gòu)參數(shù)；②由于剛度參數(shù)的數(shù)量級(jí)遠(yuǎn)大于阻尼參數(shù)，其在協(xié)方差矩陣中起主要作用，故剛度參數(shù)識(shí)別精度高于阻尼參數(shù)，且阻尼參數(shù)震蕩幅度更大，收斂速度慢于剛度參數(shù)；③能夠準(zhǔn)確估計(jì)出結(jié)構(gòu)位移時(shí)程；④由各個(gè)階段最終識(shí)別結(jié)果看出，即使加入5%白噪聲，最終收斂精度仍然很高，剛度參數(shù)識(shí)別誤差不大于0.2%，阻尼參數(shù)識(shí)別誤差不大于4%，具有較高的魯棒性；⑤所提出算法數(shù)值穩(wěn)定，不存在因矩陣奇異而計(jì)算中斷的問(wèn)題。

表1 線性系統(tǒng)時(shí)變參數(shù)識(shí)別結(jié)果Tab.1 Time-varying parameter identification results of linear system

2.2 三自由度Bouc-Wen模型系統(tǒng)

考慮一個(gè)三自由度剪切型框架結(jié)構(gòu)，底層采用Bouc-Wen滯回模型，受地震荷載激勵(lì)，其運(yùn)動(dòng)方程可寫為

(59)

(a)

本算例中，取m1=450 kg，m2=400.5 kg，m3=350.5 kg；k1=20.5 kN/m，k2=23.5 kN/m，k3=23.5 kN/m；c1=0.205 kN·s/m，c2=0.255 kN·s/m，c3=0.255 kN·s/m；α=0.2，β=2，γ=1，n=1，由于該模型參數(shù)的冗余性，n不作為待識(shí)別參數(shù)。地震激勵(lì)選取El Centro地震波，采樣頻率100 Hz，地震持續(xù)時(shí)間31.2 s。

(a)

本文中認(rèn)為地震輸入已知，觀測(cè)量為各層絕對(duì)加速度。為模擬實(shí)際觀測(cè)中噪聲的干擾，在模擬的量測(cè)加速度數(shù)據(jù)中加入5%RMS的高斯白噪聲，然后使用低通濾波去除加速度時(shí)程中的高頻成分，濾波截?cái)囝l率為20 Hz，為了驗(yàn)證MSTSRUKF在識(shí)別非線性結(jié)構(gòu)參數(shù)突變的有效性，設(shè)定當(dāng)t=15 s時(shí)：結(jié)構(gòu)一層剛度由k1=20.5 kN/m突變到k1=14 kN/m，結(jié)構(gòu)二層剛度k2=23.5 kN/m突變到k2=16 kN/m，三層剛度k3=23.5 kN/m突變到k3=16 kN/m。狀態(tài)向量初值取為X0=[0,0,0,0,0,0,0,16,16,16,0.16,0.16,0.16,0.16,1.6,0.8]T

結(jié)構(gòu)參數(shù)識(shí)別結(jié)果，如圖3所示。結(jié)構(gòu)各層位移識(shí)別結(jié)果，如圖4所示。第一層滯回曲線及滯變位移識(shí)別結(jié)果，分別如圖5、圖6所示。

(a)

(a)

圖5 第一層滯回曲線識(shí)別結(jié)果Fig.5 Hysteric loop estimation results of 1st floor

圖6 第一層滯變位移識(shí)別結(jié)果Fig.6 Hysteric displacement estimation results of 1st floor

若以1～15 s為第一階段，15.0～31.2 s為第二階段，不同階段參數(shù)最終識(shí)別結(jié)果,如表2所示。

由圖3、圖4、圖5、圖6以及表2可以看出，本文提出的MSTSRUKF：①對(duì)于非線性系統(tǒng)具有良好的識(shí)別效果，能較為準(zhǔn)確地識(shí)別各層位移；②能夠有效識(shí)別到參數(shù)突變，剛度參數(shù)在經(jīng)過(guò)短暫震蕩后很快收斂到真值；③根據(jù)先驗(yàn)知識(shí)調(diào)整阻尼項(xiàng)在漸消因子中對(duì)應(yīng)μk值，阻尼項(xiàng)經(jīng)較小幅度的震蕩后，也很快收斂到真值；④由于剛度參數(shù)的數(shù)量級(jí)遠(yuǎn)大于阻尼參數(shù)的數(shù)量級(jí)，故剛度參數(shù)的識(shí)別精度高于阻尼參數(shù)；⑤結(jié)構(gòu)參數(shù)突變后，描述Bouc-Wen模型系統(tǒng)的參數(shù)識(shí)別精度有所降低，最高誤差達(dá)到-11.19%；⑥所提方法數(shù)值計(jì)算穩(wěn)定，對(duì)于強(qiáng)非線性系統(tǒng)仍能穩(wěn)定、有效運(yùn)行。

表2 Bouc-Wen模型系統(tǒng)時(shí)變參數(shù)識(shí)別結(jié)果Tab.2 Time-varying parameter identification results of Bouc-Wen model system

2.3 三自由度杜芬結(jié)構(gòu)系統(tǒng)

考慮一個(gè)三自由度剪切型杜芬系統(tǒng)遭受地震激勵(lì)，其運(yùn)動(dòng)方程可以寫為

(60)

本算例中取m1=m2=m3=1 000 kg，c1=c2=c3=0.6 kN·s/m，k1=120 kN/m，k2=120 kN/m，k3=60 kN/m，kd1=200 kN/m3，kd2=200 kN/m3，kd3=-50 kN/m3。地震激勵(lì)選取El Centro地震波，采樣頻率100 Hz，地震持續(xù)時(shí)間31.2 s。

本文中認(rèn)為地震輸入已知，觀測(cè)量為各層絕對(duì)加速度。為模擬實(shí)際觀測(cè)中噪聲的干擾，在模擬的量測(cè)加速度數(shù)據(jù)中加入5%RMS的高斯白噪聲，然后使用低通濾波去除加速度時(shí)程中的高頻成分，濾波截?cái)囝l率為20 Hz，為了驗(yàn)證MSTSRUKF在識(shí)別非線性結(jié)構(gòu)參數(shù)突變的有效性，設(shè)定當(dāng)t=15 s時(shí)，結(jié)構(gòu)一層剛度由k1=120 kN/m突變到k1=100 kN/m，結(jié)構(gòu)二層剛度k2=120 kN/m突變到k2=100 kN/m。狀態(tài)向量初值取為X0=[0,0,0,0,0,0,90,90,50,0,0,0,0.3,0.3,0.3]T。

結(jié)構(gòu)參數(shù)識(shí)別結(jié)果,如圖7所示，結(jié)構(gòu)各層位移識(shí)別結(jié)果,如圖8所示。

(a)

(a)

若以1～15 s為第一階段，15.0～31.2 s為第二階段，不同階段參數(shù)最終識(shí)別結(jié)果,如表3所示。

表3 Duffing系統(tǒng)時(shí)變參數(shù)識(shí)別結(jié)果Tab.3 Time-varying parameter identification results of Duffing system

由圖7、圖8及表3可以看出，本文提出的MSTSRUKF：①能夠準(zhǔn)確估計(jì)Duffing系統(tǒng)位移時(shí)程；②能夠有效追蹤到結(jié)構(gòu)剛度突變，并很快收斂到真值；③根據(jù)先驗(yàn)知識(shí)調(diào)整阻尼項(xiàng)在漸消因子中對(duì)應(yīng)μk值，阻尼參數(shù)微小震蕩后快速收斂到真值；④與位移三次方相關(guān)的剛度參數(shù)識(shí)別誤差略微偏大，最大誤差為5.54%；⑤計(jì)算過(guò)程數(shù)值穩(wěn)定，不存在因數(shù)學(xué)計(jì)算不穩(wěn)定而意外終止的問(wèn)題。

3 結(jié) 論

針對(duì)土木工程結(jié)構(gòu)地震作用下時(shí)變參數(shù)識(shí)別問(wèn)題，提出改進(jìn)的強(qiáng)追蹤平方根無(wú)跡卡爾曼濾波算法。算法克服了傳統(tǒng)UKF及SRUKF協(xié)方差矩陣平方根遞推過(guò)程中數(shù)值計(jì)算不穩(wěn)定的問(wèn)題，使遞推過(guò)程無(wú)條件數(shù)值穩(wěn)定；其次使用量測(cè)矩陣Jacobian矩陣的等價(jià)形式，避免復(fù)雜系統(tǒng)求解Jacobian矩陣，簡(jiǎn)化計(jì)算方法，擴(kuò)展該方法的應(yīng)用范圍；最后引入強(qiáng)追蹤濾波技術(shù)，實(shí)現(xiàn)時(shí)變結(jié)構(gòu)的參數(shù)識(shí)別。數(shù)值分析結(jié)果表明：

(1)線性系統(tǒng)數(shù)學(xué)模型相對(duì)簡(jiǎn)單，其時(shí)變參數(shù)識(shí)別結(jié)果優(yōu)于非線性系統(tǒng)，因剛度參數(shù)與阻尼參數(shù)數(shù)量級(jí)相差較大，剛度參數(shù)識(shí)別結(jié)果優(yōu)于阻尼參數(shù)。

(2)對(duì)于Bouc-Wen模型系統(tǒng)，由于控制滯回特性的參數(shù)較多，而系統(tǒng)對(duì)不同參數(shù)的敏感性也不同，故應(yīng)科學(xué)選取敏感參數(shù)的初值及協(xié)方差矩陣中對(duì)應(yīng)的元素值，避免識(shí)別過(guò)程中系統(tǒng)發(fā)散。

(3)對(duì)于杜芬系統(tǒng)，與位移三次方對(duì)應(yīng)的剛度參數(shù)識(shí)別結(jié)果精度低于與一次項(xiàng)對(duì)應(yīng)的剛度參數(shù)，說(shuō)明其對(duì)系統(tǒng)的影響程度不如一次項(xiàng)對(duì)應(yīng)的剛度參數(shù)。

(4)對(duì)于時(shí)變參數(shù)的線性系統(tǒng)和非線性系統(tǒng)，所提方法均能較好地識(shí)別結(jié)構(gòu)參數(shù)，結(jié)構(gòu)狀態(tài)預(yù)測(cè)結(jié)果在初始階段有一定誤差，待參數(shù)收斂后預(yù)測(cè)結(jié)構(gòu)狀態(tài)也與真實(shí)狀態(tài)吻合良好。

(5)在數(shù)值模擬過(guò)程中，所提出的算法數(shù)值計(jì)算穩(wěn)定，最終識(shí)別結(jié)果表明本文提出的方法在避免求解Jacobian矩陣后能夠準(zhǔn)確識(shí)別結(jié)構(gòu)參數(shù)。

針對(duì)時(shí)時(shí)參數(shù)突變的情況因收斂需要過(guò)程，當(dāng)結(jié)構(gòu)剛度、阻尼以及控制滯回特性的參數(shù)變化在合理范圍內(nèi)時(shí)，所提算法能夠收斂；本算法確保了遞推過(guò)程計(jì)算的穩(wěn)定性，但實(shí)際工程中觀測(cè)量數(shù)目遠(yuǎn)小于結(jié)構(gòu)的自由度數(shù)目，實(shí)際應(yīng)用效果還需進(jìn)一步驗(yàn)證。