抗撞結構樁基承載能力的撞擊頭部設計方法

荀 舟，雷正保

(長沙理工大學 大型結構碰撞實驗室，長沙 410114)

護欄系統，這條道路上的“生命線”，在重定向失控車輛、吸收撞擊能量、避免二次撞擊等方面發揮著重要的作用[1]。在撞擊過程中，護欄立柱旋轉、斷裂、彎曲、扭曲或組合失效模式決定了護欄系統的性能，如果立柱不是在土壤中充分旋轉而是斷裂或屈服，護欄系統的承載能力會遠低于預期的目標[2]。在對護欄系統和部件的承載能力進行碰撞試驗檢測的過程中，由于足尺碰撞試驗需要花費大量的時間和費用，部分學者采用碰撞仿真分析進行研究。都雪靜等[3]通過建立有限元仿真模型分析了不同車型和碰撞速度下高速公路波形梁護欄的耐撞性能。Atahan等[4]對12 m長的護欄端部處理進行了詳細的有限元分析，以評估其耐撞性。Sassi等[5]建立了剛性撞擊頭撞擊立柱的有限元模型，并比較分析了新的土壤建模方法。此外，為減少實施碰撞試驗需花費的時間和費用，一種可重復使用安裝在車輪上的剛性構架的部件被用于碰撞路邊各種設施。典型的護欄立柱動態沖擊試驗是由一個連接到臺車前端的圓柱形撞擊頭撞擊立柱，安裝在臺車重心處的加速度傳感器被用于測臺車縱向的加速度，安裝在立柱不同位置的應變計被用于測立柱內部的彎矩、帶狀開關測臺車初始撞擊速度、拉線傳感器測撞擊點處的位移。

在歷史的動態沖擊試驗中，研究者總是希望試驗結果能充分地反映立柱與土壤之間的相互作用，即試驗結果能充分地反映樁基的承載能力。撞擊初始時刻撞擊頭施加的力垂直于立柱，試驗過程中立柱旋轉，撞擊頭施加的力不再垂直于立柱，撞擊力的部分分力會被用來將臺車抬起，接觸點也會沿著立柱的表面滑動，如圖1所示。這會導致試驗結果并不能充分地反映樁基的承載能力。

圖1 單柱受力示意圖Fig.1 Force diagram of single post

Herr等[6]采用符合FHWA規范的臺車，一個圓柱形撞擊頭連接到臺車的前端，并未提及撞擊頭的結構和大小。大多數撞擊頭由直徑203 mm、厚12.5 mm的標準鋼管制成[7-9]，并未見其關于撞擊頭影響的分析。Wu等[10]采用木制長方體塊作為臺車撞擊頭，并未提及尺寸。Reid等[11]建議采用可壓潰的撞擊頭避免慣性效應的影響。動態沖擊試驗中現存的臺車撞擊頭的結構并未考慮到立柱旋轉對試驗結果的影響。

獲取毀滅性碰撞時的特征參數需進行毀滅性碰撞試驗，然而，目前的動態沖擊試驗得到的試驗結果并沒有考慮臺車撞擊頭對反映真實的樁基承載能力的影響，這制約著從臺車動態沖擊試驗中獲取毀滅性碰撞時準確的特征參數。本研究的主要目的是彌補臺車動態沖擊試驗得到的試驗結果不能充分地反映樁基真實的承載能力的不足。本研究根據動態沖擊試驗建立了有限元仿真模型，并將有限元仿真模型校準為臺車撞擊單柱的動態沖擊試驗，并利用經過驗證的有限元仿真模型研究樁基承載能力。

1 埋入硬黏土中的護欄立柱動態試驗

為建立有限元模型的可信度，應將有限元仿真結果校準為動態試驗的結果。Lim等[12]在天然的硬黏土中進行了臺車撞擊單柱的動態沖擊試驗，如圖2所示。并保留了試驗結果以驗證有限元模型。采用空心HSS6X6X3/8鋼柱埋入土中1.01 m進行單柱試驗，用于動態試驗的臺車質量為900 kg，臺車速度為16 km/h，實際撞擊速度為16.4 km/h。安裝于臺車質心處的加速度傳感器和安裝于立柱上的加速度傳感器分別用來記錄撞擊過程中臺車的減速度、立柱的速度和位移，立柱上的加速度傳感器安裝位置如圖3所示。打入開口柱時，允許土進入柱內，測量柱內堵土高度為756 mm。立柱的撓度由高速攝像機記錄的數據分析得來，測點位置，如圖3所示。由于試驗用土是現有的硬黏土而不是人造黏土坑，在沖擊試驗之前進行了土壤試驗，土壤試驗數據用于有限元仿真。

圖2 臺車撞擊單柱試驗Fig.2 Bogie impact single post test

圖3 試驗示意圖 (mm)Fig.3 Diagram of test (mm)

2 有限元仿真模型

2.1 土基建模

采用八節點六面體單元將土基建模為一個圓柱體土塊，圓柱體的面中心埋入立柱。通過多次仿真分析，當土基直徑和深度分別為3 000 mm、2 000 mm時，可以節省較多的模型計算時間，且仿真結果趨于穩定。將土基分為兩個同軸的圓塊，靠近立柱的土壤網格尺寸小，以捕捉土體變形，遠離立柱的土壤網格尺寸大，以節省計算時間。

硬黏土采用各向同性彈塑性破壞模型建模，各向同性彈塑性破壞模型的材料卡片具體參數，如表1所示[12]。此外，單元侵蝕選項選擇為1.0，即由于拉伸而失效的單元不會被從模型中移除。打入開口柱時，進入立柱內的土壤與土基的建模一致，立柱內堵土高度為756 mm，并將立柱內的土壤與土基的接觸面上的節點融合。

表1 材料卡片具體參數Tab.1 Specific parameters of material card

2.2 立柱、臺車建模

由于鋼材料是一種具有應變率效應的材料，所以采用帶有應變率效應的分段線性塑性材料模型(MAT024)模擬鋼模型，并且應變率效應由Cowper等[13]提出的方程來描述立柱采用四節點殼單元建模，立柱與地基之間的縫隙距離為立柱厚度的一半。在有限元模擬中建立了臺車有限元模型，用以近似試驗的臺車，其臺車有限元模型的形狀盡量與真實車輛相當，前后輪距為1 500 mm，軸距為3 000 mm，并且臺車總質量和撞擊速度與試驗一致，臺車有限元模型質量為900 kg，初始撞擊速度為16.4 km/h，如圖4所示。

式中：σ′和σ分別為動態應力和準靜態應力；D和q為Cowper-Symonds系數，D=40 s-1，q=5[14];D=40 s-1，q=5，靜態屈服應力235 MPa是Cowper-Symonds模型模擬鋼材料的輸入參數。

2.3 其他建模

為輸出立柱上的加速度傳感器的數據，在立柱撞擊面的背面，撞擊點的水平面上建立了加速度傳感器有限元模型，如圖4所示。考慮到由于土體自質量引起的土壓力，對立柱、臺車和土基模型施加了重力場，并約束了土基模型下端節點的6個自由度。

圖4 有限元仿真模型Fig.4 Finite element simulation model

臺車、立柱、土基的有限元模型自身采用了CONTACT AUTOMATIC SINGLE SURFACE接觸算法，以防止各部分在碰撞過程中自身發生穿透。臺車撞擊頭與立柱、立柱與土基之間的接觸采用CONTACT AUTOMATIC SURFACE TO SURFACE接觸算法，計算了臺車撞擊頭與立柱的接觸面的作用力并輸出，用以代替試驗臺車質心處的加速度傳感器得到的力曲線，并且臺車與土基之間創建了地面接觸。

至此完成臺車-立柱-土基有限元建模，立柱上的加速度傳感器的輸出數據和立柱與撞擊頭的接觸面力將作為驗證有限元模型可信度的依據。

2.4 仿真結果與驗證

有限元仿真模擬進行了200 ms，輸出了立柱背面的加速度傳感器測量的加速度數據、立柱與臺車撞擊頭的接觸面力。所有數據均采用符合SAE J211/1規范的SAE Class 60 Butterworth濾波器進行濾波。將有限元仿真得到的加速度曲線、立柱與臺車撞擊頭的接觸面力曲線分別與試驗數據進行比較，如圖5、圖6所示。

圖5 試驗與仿真加速度曲線比較Fig.5 Comparison of acceleration curves between test and simulation

圖6 試驗與仿真力曲線比較Fig.6 Comparison of force curves between test and simulation

有限元仿真中得到的加速度曲線與試驗中得到的加速度曲線在曲線形態和峰值方面表現出良好的一致性，有限元仿真中得到的力曲線的形態和峰值與試驗得到的較為接近，此仿真過程中的最大載荷為57.8 kN。通過仿真得到的加速度與力曲線的雙重驗證，此有限元仿真模型被認為是可信的。對仿真動畫進行回顧，如圖7所示。在碰撞過程中臺車大約在0.087 s時運動停止，隨后開始反彈。土壤在碰撞方向的最大永久變形大約為134 mm，立柱的旋轉中心大約位于地面以下791 mm處。

圖7 土壤變形Fig.7 Soil deformation

3 反求撞擊頭輪廓

撞擊初始時刻撞擊頭施加的力垂直于立柱，試驗過程中立柱旋轉，撞擊頭施加的力不再垂直于立柱，不同大小、結構的撞擊頭產生的不同影響尤其明顯，這導致試驗結果并不能充分地反映樁基真實的承載能力。此外，撞擊點沿立柱表面滑動，在碰撞過程中得到的試驗結果并不是載荷施加在同一點的結果。本研究參考反求凸輪輪廓的思路[15]，根據立柱倒伏的路徑反求撞擊頭的輪廓形狀和大小，反求思路如圖8所示。

圖8 反求撞擊頭輪廓示意圖Fig.8 Reverse design of the outline of impact head

圖8所示為將力傳感器安裝在立柱上的臺車動態沖擊試驗，取力傳感器的中心位置到地面的垂直距離為撞擊試驗的撞擊高度b，立柱的旋轉中心到地面的垂直距離為旋轉距離a，力傳感器在撞擊方向上的長度為c。將立柱和力傳感器簡化，取初始位置時三維力傳感器接觸面的中心位置為初始撞擊點，以立柱旋轉中心的水平面與立柱撞擊外表面的交點為坐標原點。連接立柱在倒伏過程中任意位置時的力傳感器接觸面的中心與立柱的旋轉中心，并延長至初始位置時三維力傳感器中心的水平線上，此時此直線與旋轉點水平面的夾角為θ，如圖8所示。旋轉點與力傳感器接觸面的中心的距離為旋轉半徑R，R的表達式為

(1)

通過初始位置時三維力傳感器接觸面的中心位置作立柱倒伏后三維力傳感器接觸面中心與立柱旋轉中心連線的平行線，交此時立柱倒伏位置的三維力傳感器接觸面中心的水平線于一點A，A點的坐標為

(2)

Ay=Rsinθ

(3)

A點即為撞擊頭輪廓上的一點。將立柱的每一倒伏角度對應的A點用光滑的曲線連接，即為撞擊頭的輪廓形狀，將得到的圓弧輪廓用圓擬合后，可截取部分圓作為撞擊頭輪廓。

對于目前通過測臺車質心處的加速度間接測撞擊力的動態沖擊試驗，此反求臺車撞擊頭的方法同樣適用，但式(1)所求旋轉半徑即為撞擊點到立柱旋轉點之間的距離。

此反求思路可以理解為：碰撞發生后在立柱倒伏過程中，撞擊頭向前平移，撞擊點沿撞擊頭的接觸面向下移動，撞擊頭與立柱在倒伏路徑上的每一位置相接觸，或者說立柱每一倒伏角度θ，撞擊頭輪廓上總有一點與撞擊點相接觸。反求出立柱倒伏時立柱上的同一撞擊點相對于初始位置的輪廓點，就確定了撞擊頭的輪廓形狀。這樣反求出的撞擊頭在立柱倒伏過程中總與同一撞擊點近似為點接觸，并且施加在立柱上的力總是垂直于立柱，如圖9所示。

圖9 撞擊頭碰撞過程示意圖Fig.9 Diagram of collision process of impact head

4 反求撞擊頭仿真分析

4.1 反求撞擊頭仿真建模

為驗證反求的撞擊頭能夠反映樁基真實的承載能力，將第3章反求撞擊頭輪廓的設計方法應用于埋入硬黏土中的護欄立柱動態試驗中，即將反求的撞擊頭替代動態試驗中的原撞擊頭進行仿真分析。

由仿真模擬的結果得知立柱的旋轉點在地面以下791 mm處，即在反求撞擊頭輪廓方法中a為791 mm，撞擊高度b為356 mm。根據反求撞擊頭輪廓的方法，立柱每旋轉到任意位置，根據同一撞擊點的位置得到撞擊頭輪廓上對應的一個A點，將這些A點用光滑的曲線連接，得到撞擊頭輪廓形狀。本研究中，取立柱每倒伏5°的位置反求撞擊頭輪廓上對應的A點，各A點相對于坐標原點的坐標，如表2所示。表2中：θ的最小取值為45°，此時的縱坐標值為811 mm，而當θ取40°時，縱坐標值比a值791 mm小，意味著撞擊頭輪廓在地面以下，這與實際情況不符，故取地面以上的輪廓對應的A點。輪廓上的各A點用圓擬合，所得圓即撞擊頭輪廓的半徑為606 mm，如圖10所示。

表2 A點坐標Tab.2 Coordinates of point A

圖10 擬合圓Fig.10 Fitting circle

擬合圓的圓心相對于坐標原點的坐標為(-555,1 381)，截取初始撞擊點水平線以下、地面以上的撞擊頭輪廓的一部分。臺車有限元模型的原撞擊頭被替換為反求的撞擊頭，并設置鋼板焊接加固，但臺車的有限元模型參數、總質量、撞擊速度等不變，且臺車撞擊頭與立柱接觸撞擊的距離和撞擊高度不變，如圖11所示。

圖11 反求撞擊頭有限元仿真模型Fig.11 Finite element simulation model of impact head based on reverse design

4.2 反求撞擊頭仿真結果

反求撞擊頭的仿真模擬結果與原撞擊頭的仿真模擬結果的比較，如圖12所示。反求的撞擊頭得到的力曲線最大載荷大約為59.1 kN，比原撞擊頭的力曲線的最大載荷57.8 kN增加了1.3 kN。在碰撞發生前期，可能由于土基未被完全壓實，前期力曲線沒有較大變化。在碰撞發生的后期，撞擊頭施加的力在碰撞過程中近似垂直于立柱，反求的撞擊頭的力曲線幾乎都在原撞擊頭力曲線的上方，試驗結果反映樁基真實的承載能力體現于此。

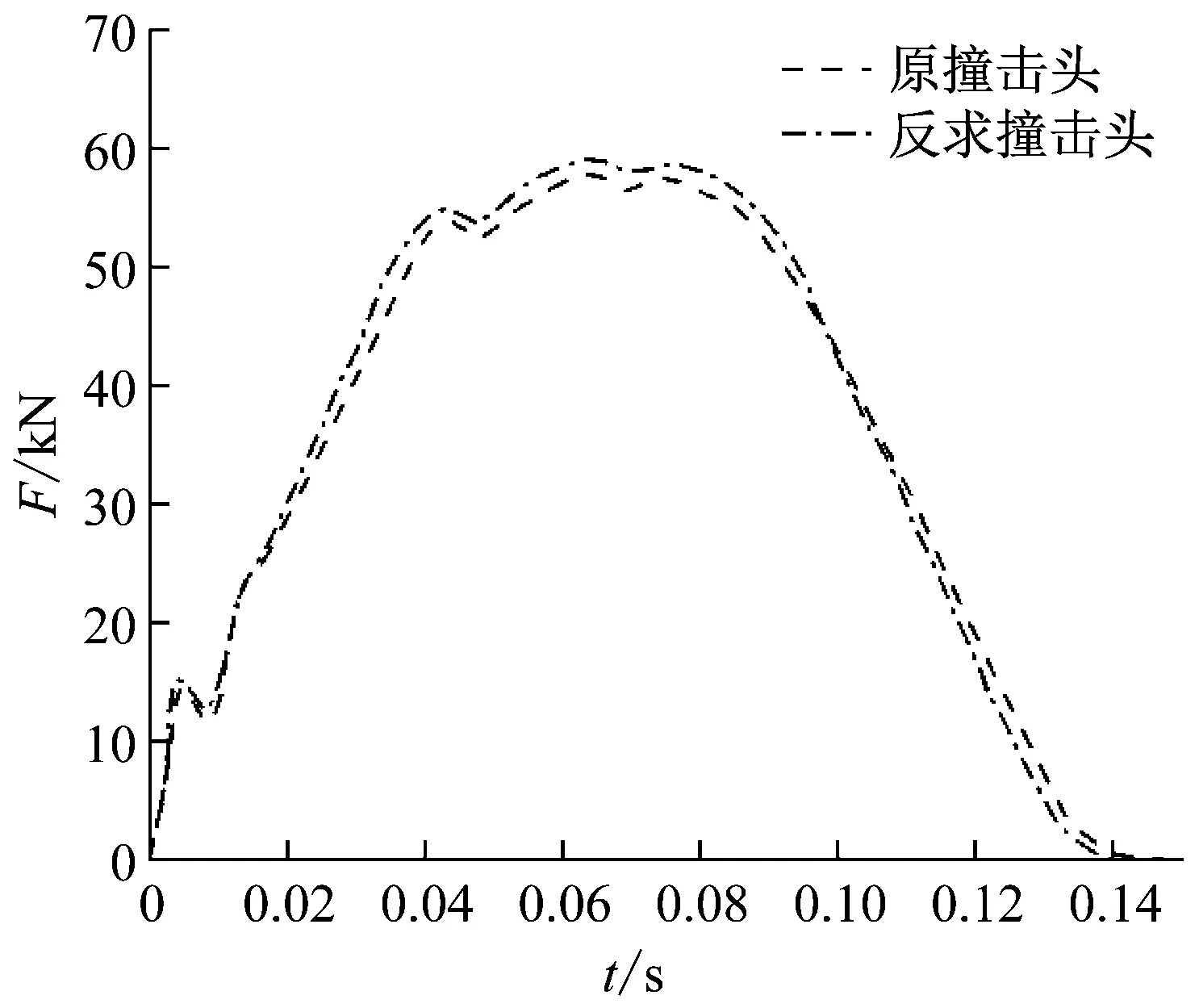
圖12 反求撞擊頭與原撞擊頭仿真結果對比Fig.12 Comparison of test curves between reverse design impact head and original impact head

5 結 論

(1)本研究參考反求凸輪輪廓的設計思想，提出了根據立柱倒伏的路徑反求撞擊頭輪廓的設計方法。

(2)建立了臺車撞擊埋入硬黏土中的單柱有限元仿真模型，并成功將其校準為臺車動態沖擊試驗，為此類有限元仿真研究提供了借鑒價值。

(3)根據本研究的方法反求出的動態沖擊試驗用撞擊頭能夠反映樁基真實的承載能力。