基于S-ALE 方法的圓柱體垂直出水破冰研究1)

汪春輝 王嘉安 王 超 郭春雨 朱廣元

(哈爾濱工程大學船舶工程學院，哈爾濱 150001)

引言

在極區，平整冰與海洋結構物間的相互作用形式主要為擠壓破壞和彎曲破壞，冰層受結構物作用產生斷裂破碎、裂紋擴展和滑移清除過程[1-4].在某些特殊情況，結構物需要上浮穿透冰層破出水面，對冰層施以自下而上的垂向載荷，而冰層垂直貫穿破裂過程十分復雜.

學界對冰與結構物垂直相互作用的研究還不充分，國內外相關研究主要以試驗和理論方法為主.由于試驗條件要求苛刻及數值技術的發展，一些具備完善冰作用機理的數值方法成為解決這些問題的好方法.并且海冰是一種復雜的材料，有許多因素會影響冰的物理特性，例如，溫度孔隙率和鹽度、速率依賴性.由于冰可發生大而復雜的變形，模擬冰與結構的相互作用是一個巨大的挑戰.

目前，有限元方法(FEM)、離散元方法(DEM)、光滑粒子法(SPH)和近場動力學(PD)等數值模擬方法已被用于模擬冰與結構物間的相互作用，本文采用有限元方法開展圓柱體垂直出水破冰研究.針對水下結構物在冰層下方上浮至破出水面的過程的研究在世界范圍內仍處于起步階段，國內外公開資料極其稀少.因此利用有限元方法分析結構物與冰層垂直相互作用進展可以參考船與冰相互接觸的研究資料[5-7].

針對冰與結構物耦合作用有限元數值分析方法，國際上已有大量的研究探索.Ehlers 和Kujala[8]在LS-DYNA 有限元軟件中使用彈塑性應變率材料模擬冰的彎曲行為，并與4 點彎曲試驗結果進行對比.Polach 和Franzvon[9]應用LS-DYNA 有限元軟件采用MAT_DAMAGE_3 材料模擬冰的力學特性，并基于損傷力學對數學模型進行分析，將模擬結果與冰池試驗結果對比.Gagnon[10]提出了一種彈性線性硬化材料，可模擬冰力學特征，但不能模擬冰的破壞斷裂行為.Wang 和Derradji-Aouat[11]基于罰函數法及拉格朗日歐拉法模擬碎冰對系泊結構的作用過程，以評估系泊結構的整體載荷.Ranta 等[12]通過FEM-DEM 耦合方法構建冰與結構物相互作用二維數值模型，利用多元回歸線性數學模型和變量消元法對冰載荷特征值分析，探究冰載荷影響因素.國內方面，郭春雨等[13]基于LS-DYNA 有限元軟件模擬了極地船和浮冰的耦合作用過程，實現了冰區船舶在碎冰區域的航行阻力預報.Wang 等[14]應用FEM方法與DEM-CFD 方法模擬了冰區船舶在冰緣區的航行過程，并將數值模擬結果與模型試驗對比，分析了碎冰載荷的主要影響因素.黃焱等[15]基于FEM方法構建并分析了固定約束及摩擦約束邊界條件下的冰溫度膨脹力，發現固定約束會造成高度的應力集中.任奕舟和鄒早建[16]、王峰[17]基于FEM 方法，通過粘聚力單元和彈塑性冰本構模型構建船舶與海冰碰撞場景的數值仿真，驗證了粘聚元方法模擬海冰的準確性與可行性.Chen 等[18]應用FEM-SPH 方法建立了錐體和破冰船與平整冰相互作用的數值模型，預測了破冰阻力及碎冰堆積過程.

本文應用 LS-DYNA 有限元軟件采用結構化-任意拉格朗日歐拉 (S-ALE)流固耦合方法及罰函數接觸算法，建立了冰、水、結構物耦合作用數值模擬方法，自主搭建了圓柱體垂直貫穿冰層試驗臺架.通過冰梁結構4 點彎曲及楔形體入水數值模擬，驗證了彈塑性應變率本構材料表征冰力學特性的準確性和流固耦合方法的可行性，對比了無水環境下圓柱體垂直貫穿冰層和圓柱體垂直出水破冰過程中的冰載荷、冰層撓度變化、冰層應力響應及斷裂現象，以期為冰層與海洋結構物垂向相互作用研究提供參考.

1 理論基礎

LS-DYNA 有限元軟件被廣泛應用于航天、航海和武器裝備等工程制造領域.由于LS-DYNA 有限元軟件包在結構計算、材料損傷破壞等領域的優勢，越來越多的學者將其應用于船冰碰撞、冰槳切削等冰工程方面的研究中，運用Lagrange 格式的顯式中心差分法計算大變形的結構物與冰層耦合作用問題.本文采取結構化任意拉格朗日歐拉方法，基于罰函數流固耦合算法模擬圓柱體上浮垂直出水破冰中冰、水、結構物耦合作用的強非線性動態過程.

1.1 結構化-任意拉格朗日歐拉流固耦合方法

結構化任意拉格朗日歐拉方法原理上是一種基于統一連續介質的動量守恒方程的二階精度的平流算法[19].通過接觸算法獲取固體之間的接觸作用時的界面力，能夠有效解決物體在空間上存在大位移同時本身存在大變形問題.在S-ALE 計算中，定義了材料域和參考域，材料的速度為u，參考系的移動速度為v，速度差u-v表示為w，由此可對S-ALE 計算方法的控制方程進行推導，如下所示

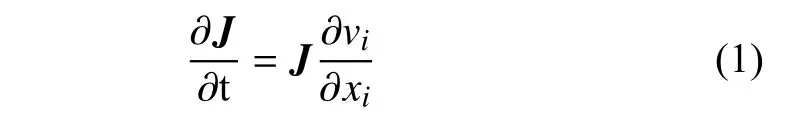
式中J為雅可比矩陣，表示兩個域的相對體積微分.

S-ALE 公式中的材料時間導數寫成公式

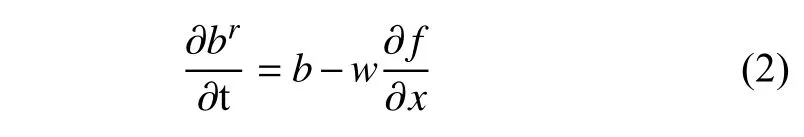
式中，br表示b的參考域函數.

S-ALE 方法的質量、動量以及能量守恒方程如下

1.2 罰函數接觸算法

罰函數接觸算法將可能發生接觸作用的兩個表面分別定義為主表面和從表面，發生穿透時，類似在主表面和從表面之間放置一系列法向彈簧，彈簧的作用是為了限制穿透，彈簧的力被稱為界面接觸力.

罰函數法的接觸力由下面計算公式得出

式中k為單元接觸面剛度，δ為穿透量.

單元接觸面剛度k由如下公式決定

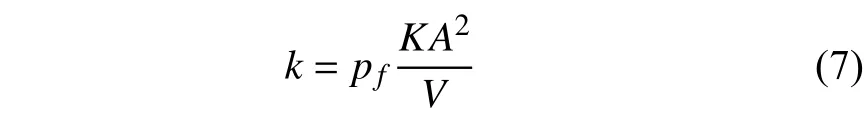
式中pf為單元接觸面剛度的懲罰因子，K是接觸單元體積彈性模量，A是接觸段面積，V是主段體積.

在數學方法上，用歐拉變量描述流體的動態，用拉格朗日變量描述結構的運動邊界，通過分布節點力和插值速度來表示流場和結構物的交互作用.該方法適用于廣泛的流固耦合應用，界面接觸力為估算求得且可能存在數值振蕩[20].

1.3 冰本構模型

冰的特性取決于溫度、應變率和載荷方向，冰在受力變形破壞過程中，受加載速率的影響，會呈現韌脆轉換現象[21].本文選用冰本構材料為彈塑性應變率本構材料*MAT _PLASTICITY_COMPRESSION_TENSION，該材料為一種各向同性的彈塑性材料，能夠模擬不同的壓縮和拉伸響應.此外，它還考慮了應變率敏感性[22-24].

該材料模型需要定義兩條用于拉伸與壓縮行為的屈服應力對有效塑性應變的曲線，以及一條應變率對壓縮屈服應力比例系數(CYSF)的曲線，用于表征應變率對壓縮強度的影響.假設彎曲強度與應變率無關，拉伸和壓縮下的屈服應力(σy)與有效塑性應變(εp)的曲線均由以下方程推導得出

式中σ0為初始屈服應力.

假定壓縮和拉伸過程中冰材料的塑性硬化模量(Ep)相同.通過Sánchez 等[25]給出的冰材料壓縮強度應變率敏感性擬合函數可以計算得出應變率()為10-3s-1時冰材料的初始壓縮屈服強度()

為了定義應變率對壓縮屈服應力比例系數的曲線，不同應變率下的壓縮強度由應變率為10-3s-1時的初始壓縮強度進一步歸一化得出，本文采用的海水冰材料應變率為10-3s-1時的初始壓縮強度為5.8 MPa.海水冰應變率和相應的壓縮屈服應力比例系數如表1 所示.對于拉伸行為，實驗結果顯示脆性破壞及應變率對冰拉伸強度的影響可以忽略不計[26].

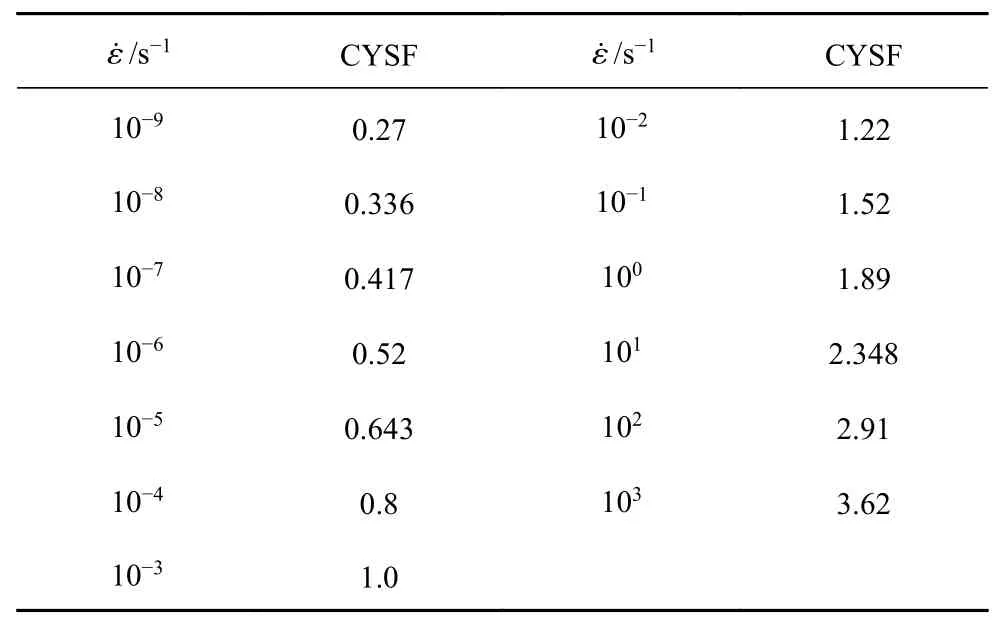
表1 海水冰應變率和壓縮屈服應力比例系數Table 1 Strain rates and compressive yield stress scale factors of sea ice

該材料模型采用等效塑性應變破壞準則，當單元的等效塑性應變達到定義的臨界值(εf)時，該單元將被刪除.可以通過調整εf值以獲得適當的彎曲響應.

2 數值計算模型

2.1 無水環境下圓柱體垂直貫穿冰層有限元模型

無水環境下圓柱體垂直貫穿冰層數值模型包含以下兩個部分:冰層和圓柱結構體，均采用拉格朗日算法進行描述.模型的幾何尺寸見下圖1，模型冰厚為3 cm，長寬均為50 cm;圓柱體直徑為3 cm，高為5 cm.冰層邊界條件采用四邊約束，圓柱體置于冰層正中心下1 cm 處.

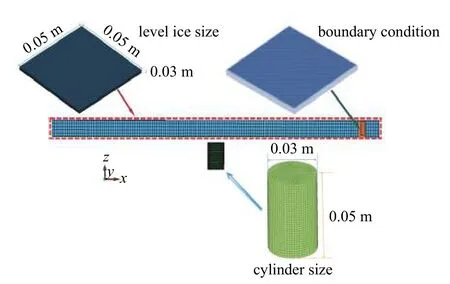
圖1 數值模型尺寸Fig.1 Size of numerical model

本文將圓柱體定義為剛體，冰層本構選用彈塑性應變率材料模型，根據數值模擬需求將冰材料分為淡水冰及海水冰兩類.主要材料參數如表2所示[24-26].

表2 主要材料參數Table 2 Main material parameters

圓柱體與冰層的相互作用以及冰單元間相互作用通過侵蝕接觸算法實現，冰層單元不斷發生破壞并刪除失效單元形成裂紋，一旦網格單元失效且接觸表面發生變化，通過侵蝕接觸可重新建立表面形狀[21].

2.2 圓柱體垂直出水破冰有限元模型

圓柱體垂直出水破冰數值模型設置與文2.1 節開展的圓柱體垂直貫穿冰層試驗工況保持一致.包含4 部分:空氣域、水域、圓柱結構體和冰層，其中，空氣域和水域采用歐拉算法進行描述，圓柱結構體和冰層仍采用拉格朗日算法進行描述.空氣域和水域的幾何尺寸及網格劃分如圖2，空氣域和水域的采用漸進式網格劃分，即應用*ALE_STRUCTURED_MESH 和*ALE_STRUCTURED_MESH_CONTROL_OINTS 關鍵字生成S-ALE 結構化網格.水和空氣通過*MAT_NULL 材料來描述，水的狀態方程為OS-GRUNEISEN 來實現，空氣的控制方程為EOSINER-POLYNOMIAL，空氣與水的相關模型參數設置如表3，圓柱體結構及冰層結構參數設置與無水環境的數值模型參數設置保持一致.

表3 空氣、水相關參數設置Table 3 Setting of air and water related parameters

圖2 圓柱體垂直出水破冰數值模型Fig.2 Numerical model of vertical upward water of cylinder breaking through level ice

針對圓柱體垂直出水破冰流固耦合問題，通過INITIAL_HYDROSTATIC_ALE 關鍵字實現流體區域靜水壓力分層，使用*CONSTRAINED_AGRANGE_IN_SOLID 關鍵字實現冰層、圓柱體和流體區域間的流固耦合作用.

3 計算方法驗證

3.1 冰本構模型驗證

Sodhi[27]指出冰層在垂向載荷作用下的破壞方式主要以彎曲破壞為主.通過對冰梁的4 點彎曲模型試驗進行數值模擬，驗證本文所用應變率彈塑性材料模擬冰彎曲破壞過程的可靠性.以Kujala 等[28]冰梁彎曲破壞模型試驗為依據，模型幾何尺寸如圖3，上方的支撐架剛性固定，下方的支撐架以2.756 mm/s勻速向上移動.冰材料參數與表2 中的海水冰材料一致.

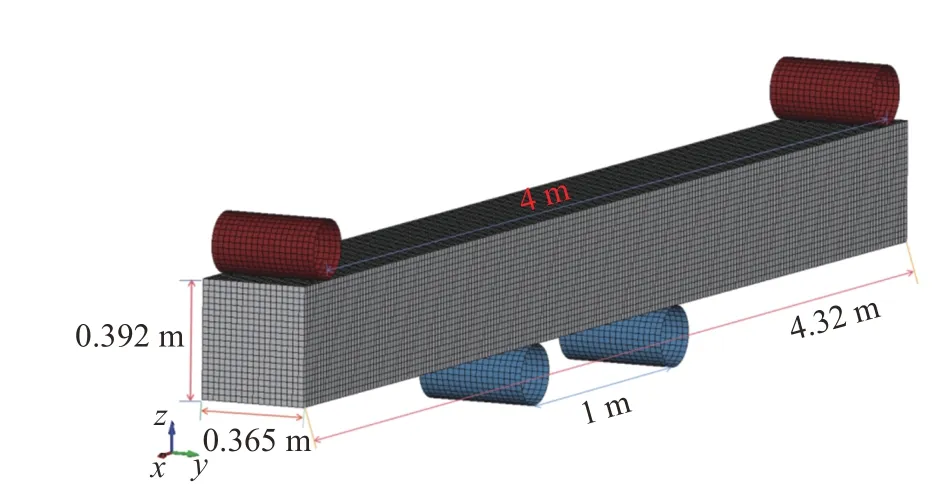
圖3 冰梁四點彎曲數值模擬幾何模型Fig.3 Geometric model for numerical simulation of four-point bending of ice beam

冰梁受到彎曲載荷后在加載支撐處形成斷裂裂紋如圖4(a)，通過對比文獻中基于SPH 方法的斷裂現象即圖5(b)發現，本文模擬的冰梁4 點彎曲斷裂現象與試驗[28]及SPH 方法[23]計算結果吻合度極高.

冰梁4 點彎曲過程的彎曲載荷-時間曲線如圖5，試驗及數值計算結果的曲線趨勢以及峰值點一致性良好.結合圖4 冰梁4 點彎曲破壞斷裂現象可以說明本文所用應變率彈塑性材料可以準確模擬冰層彎曲破裂問題.

圖5 冰梁4 點彎曲數值驗證模擬結果Fig.5 Numerical verification of simulation results of four-point bending of ice beam

3.2 圓柱體垂直貫穿冰層試驗

基于自主開發的試驗臺架、以凍結模型冰為試驗對象、開展無水環境下圓柱體垂直貫穿冰層試驗，探究該動態破冰過程的現象及破冰載荷.試驗臺架如圖6，主要儀器包括伺服電動缸、數據采集與分析處理系統和接觸式壓力傳感器等，試驗臺架主要用來固定模型冰以及搭載伺服電動缸

圖6 試驗用主要儀器Fig.6 Main instruments for test

試驗使用凍結型模型冰作為模型材料，將煮沸后的純凈水倒入模具中冷卻凝固至定型，凍結24 h定型后取出進行尺寸修正，再將修正過的模型冰放于低溫試驗箱中儲存24 h 后進行試驗，低溫試驗箱環境溫度恒定為-25 °C.為測量制備模型冰的力學性能參數，分別進行了單軸壓縮試驗和巴西圓盤試驗測量其抗壓強度及拉伸強度.單軸壓縮試驗和巴西圓盤試驗壓頭加載速率均為4 mm/s，與圓柱體垂直貫穿冰層試驗加載速率保持一致.

單軸壓縮試驗試驗選用長方體模型冰試樣，冰試樣尺寸為40 mm×40 mm×100 mm，盡可能減少冰體試樣本身對試驗結果的影響，測得模型冰試樣平均抗壓強度為2.41 MPa.單軸壓縮試驗典型破壞過程如圖7.

巴西圓盤法是一種間接測量抗拉強度的方法，能夠有效避開直拉法試驗過程中存在的冰試件夾持和加載困難的缺點[29].試驗用圓盤狀冰體試樣直徑為10 cm 厚度為5 cm，測得模型冰試樣平均拉伸強度為0.39 MPa.巴西圓盤試驗典型破壞過程如圖8.

Sodhi[27]發現冰層的垂向貫穿破裂過程中的大撓度變形僅發生于施加載荷附近區域，通常小于冰厚度的10～ 20 倍，且固定約束(四邊約束)下冰載荷穩定性優于自由約束下冰載荷穩定性，但固定約束(四邊約束)下冰載荷均值要大于自由約束下冰載荷均值.為獲得可靠的試驗結果及規律性結論，選取符合尺度效應的冰層尺寸(50 cm×50 cm×3 cm)的模型冰板并采用固定約束(四邊約束)進行多組試驗，如圖9.將模型冰板置于試驗臺架上，鋁型材扣置于模型冰上方約束冰層運動.試驗用圓柱體試樣直徑3 cm，高5 cm，壓載速率為4 mm/s，圓柱體試樣勻速上升與冰層接觸，通過數據采集系統和高速攝像機，記錄模型冰板斷裂破壞過程中冰載荷的時歷曲線以及圓柱體試樣與模型冰接觸作用時冰層破裂現象.

圖9 試驗用凍結模型冰Fig.9 Frozen model ice used in the test

圓柱體試樣與冰層接觸后，冰層試樣不會瞬間破裂，如圖10(a)，隨著圓柱體壓頭的上壓，冰層中間部分受壓發生向上彎曲，冰層四周向上翹曲，如圖10(b).隨著圓柱體試樣的進一步上壓，裂紋從冰層中部產生，瞬間擴散至冰層四周，并在四邊約束的作用下，冰層先會沿約束內側產生周向斷裂，最終被頂起形成碎冰堆，如圖10(c).

圖10 試驗現象Fig.10 Experimental phenomenon

圖10 試驗現象(續)Fig.10 Experimental phenomenon (continued)

由于在冰層的制取過程中，冰的形狀、厚度存在一定不可避免的差異，無法保證每次試驗模型完全相同，導致冰載荷極值與作用時間存在一定的差異.選取4 組3 cm 厚度冰層進行試驗重復性驗證，其試驗結果如圖11，結果表明整體試驗數據一致性良好.

圖11 冰層垂直貫穿破裂試驗重復性驗證Fig.11 Repeatability verification of vertical penetr-ation test of level ice

3.3 圓柱體垂直貫穿冰層數值模型驗證

網格質量影響數值計算精度，過多的網格往往會極大的延長數值計算時間，而數值計算采用的模型計算單元需要保證結果準確性的同時提高計算效率.由于圓柱體模型為剛體材料，網格質量影響相對較小，所以為驗證網格合理性，分別對冰層數值模型劃分大小為2.5 mm，3.5 mm 以及4 mm 的正方形網格，進行網格無關性分析.

如圖12 所示，圖中3 條曲線總體來看趨勢一致且峰值點近似相同，呈振蕩上升趨勢且冰載荷特征穩定，2.5 mm 網格單元曲線與3.5 mm 網格單元曲線擬合度良好，4 mm 網格單元曲線載荷卸載時間相對提前.所以選取冰層網格單元大小為3.5 mm，既可以保證數值精度又可以提高計算效率.

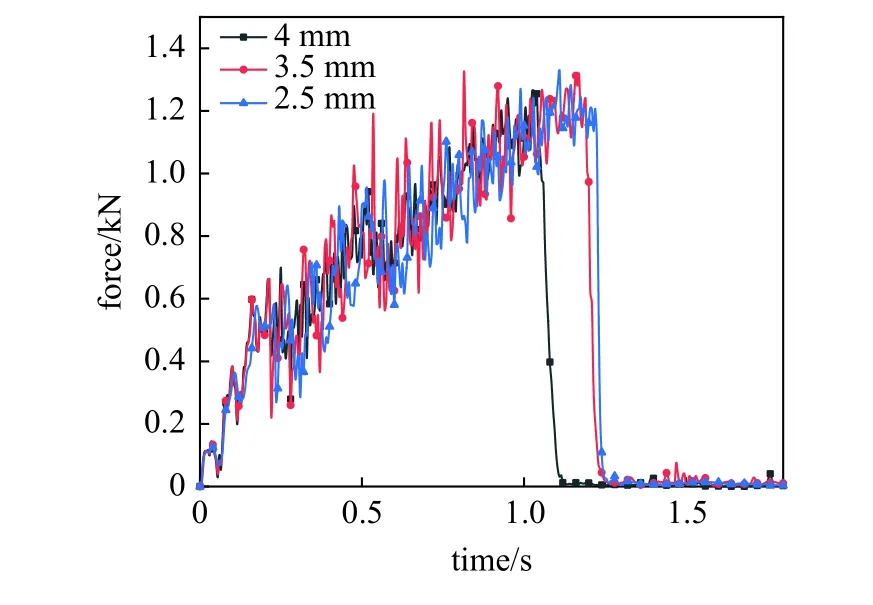
圖12 不同網格尺寸下的冰載荷時歷曲線Fig.12 Time history curve of ice load under different element sizes

開展無水環境下圓柱體垂直破冰數值仿真以驗證數值方法準確性，數值計算模型見1.2 節，冰層材料選用表2 中淡水冰材料，計算工況與上述試驗一致，圖13 為數值模擬結果.從圖13(a)應力云圖中可以看出，當圓柱體與冰層接觸而冰層并未發生斷裂現象時，冰層發生彈性變形，應力集中在冰層中心，由于冰層采用四邊約束應力區域呈環狀.隨著圓柱體與冰層的持續作用，部分冰層單元達到失效極限，出現徑向裂紋向四周擴展，裂紋相互作用進一步形成楔子，如圖13(b)所示.當圓柱體繼續上升，由于應力集中于冰層中央，導致冰層中部破碎形成碎冰堆積，冰層產生周向裂紋，隨后冰層向中心塌陷，如圖13(c)所示，對比圖10(c)可以看出冰層向中心塌陷整體現象以及破壞范圍均呈現良好的一致性，且均存在約束下的徑向裂縫在其形成后不再進一步擴展，并且由徑向裂縫形成的大塊楔形物隨圓柱體進一步加載而隨之推動.

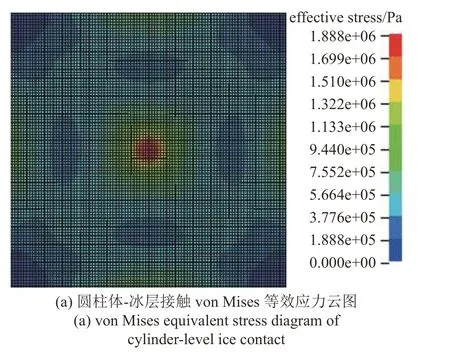
圖13 圓柱體垂直破冰數值模擬冰層破裂過程Fig.13 Numerical simulation of level ice rupture process by cylinder vertical ice breaking

圖13 圓柱體垂直破冰數值模擬冰層破裂過程(續)Fig.13 Numerical simulation of level ice rupture process by cylinder vertical ice breaking (continued)

圖14 為圓柱體垂直破冰時數值模擬與試驗結果的冰載荷時歷曲線.在圓柱體接觸冰層且勻速上升過程中，數值模擬冰載荷數據呈震蕩上升的趨勢，伴隨著冰層裂紋產生和擴展，整體趨勢、載荷峰值且突破時間均與試驗值一致.

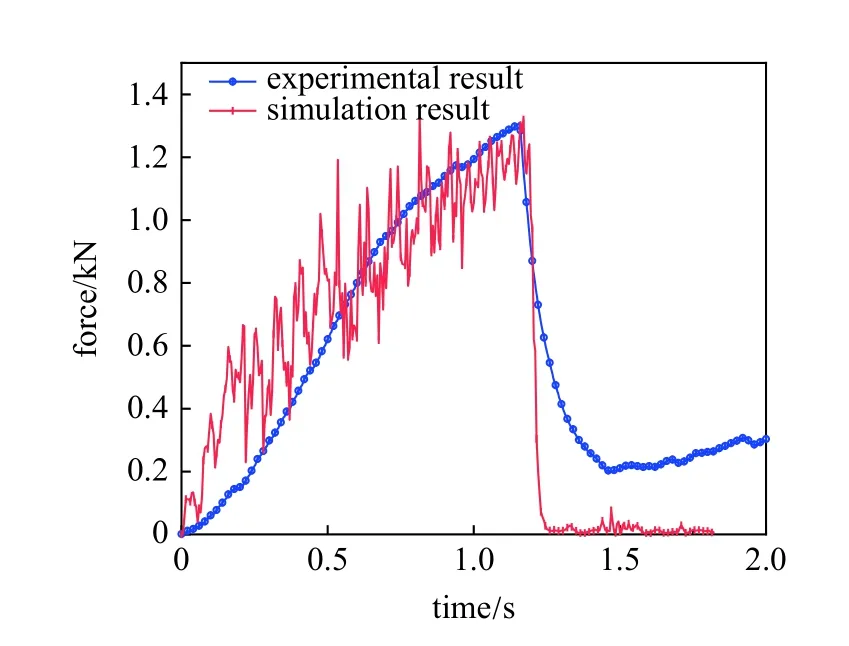
圖14 圓柱體垂直破冰載荷數值與試驗對比曲線Fig.14 Numerical and experimental comparison curve of vertical ice breaking load of cylinder

3.4 基于S-ALE 方法的楔形體入水數值模擬

為驗證使用S-ALE 方法分析流固耦合問題的準確性與可行性，應用此方法模擬了二維楔形體入水砰擊過程，并與陳光茂等[30]基于SPH 方法模擬二維楔形體入水問題的數值結果及Zhao 和Faltinsen[31]的實驗結果進行對比.

依據文獻[30]建立二維楔形體入水數值模型，水池長2.4 m，高1.3 m，以此保證入水砰擊的過程中壁面反射不會對楔形體受力產生干擾.楔形體形狀為等腰三角形，頂邊長度為0.5 m，斜升角(即斜邊與水平方向的夾角)為30°.在楔形體入水前的瞬間，它的垂向速度為6.15 m/s，隨后自由入水，計算使用的二維楔形體為實心剛體，重量為 241 kg.

圖15 為S-ALE 方法模擬的楔形體入水過程自由表面變形，與文獻[30]試驗現象一致，通過圖16入水時間0.015 8 s 時壓力分布對比圖可知S-ALE 方法數值模擬結果與文獻[30]中應用SPH 方法模擬結果相同，且圖17 中入水垂向速度隨時間變化對比曲線吻合性良好，證明了S-ALE 方法處理流固耦合問題的準確性與合理性.

圖15 楔形體入水過程自由表面變形Fig.15 Deformation of free surface of wedge during water entry

圖16 入水時間0.015 8 s 時壓力分布對比圖Fig.16 Comparison diagram of pressure distribution when water entry time is 0.015 8 s

圖16 入水時間0.015 8 s 時壓力分布對比圖(續)Fig.16 Comparison diagram of pressure distribution when water entry time is 0.015 8 s (continued)

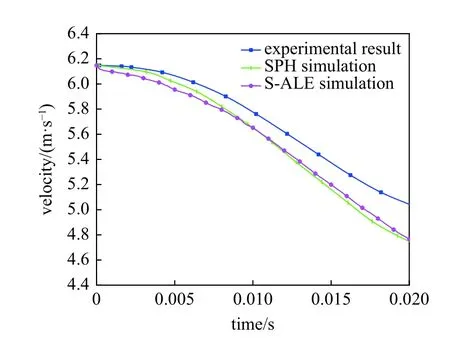
圖17 入水垂向速度隨時間變化圖Fig.17 Variation diagram of vertical velocity of water inflow with time

4 圓柱體垂直出水破冰過程計算結果分析

圓柱體垂直出水破冰數值模擬有限元模型如2.2 節所示，模型冰材料選取及模擬工況均與無水環境下圓柱體垂直貫穿冰層一致.

4.1 冰載荷分析

圓柱體垂直出水破冰和無水環境下圓柱體垂直貫穿冰層冰載荷時歷對比曲線如圖18，出水破冰時圓柱體所受冰載荷整體趨勢與無水破冰時類似，冰載荷峰值基本一致;出水破冰時冰層與圓柱體相互作用時間比無水破冰時的作用時間長，原因是在圓柱體與冰層接觸之前的近場逼近過程中，結構體與冰層之間的水由于受到結構物與被約束的冰層的雙重擠壓而預先產生的一個高壓力場，該壓力場使船-冰之間產生一個對冰層存在支撐作用的阻力，即水墊效應[32].水墊效應作用在冰層，使的冰層彈性變形階段更長，且冰層失效后未塌陷，仍然與圓柱體接觸產生作用力;出水破冰時圓柱體上浮過程中水會上升擠壓冰面，高壓力場導致圓柱體尚未與冰層接觸前發生彎曲變形從而產生撓度，所以有水環境下圓柱體與冰層的冰載荷要略晚于無水環境出現(0.08 s)，且有水情況下的冰載荷變化趨勢相對平緩.

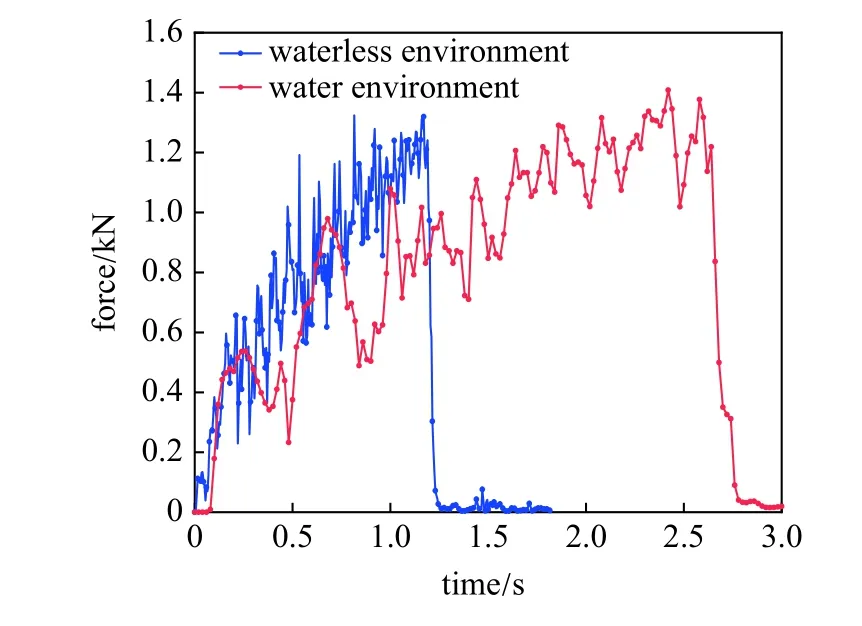
圖18 有水和無水環境下圓柱體上浮破冰冰載荷時歷曲線Fig.18 Time history curve of ice breaking load on floating cylinder in water and waterless environment

4.2 冰層撓度變化分析

圓柱體垂直出水破冰過程可分為水下上浮階段和出水破冰階段兩部分.為研究圓柱體出水破冰過程中冰層撓度變化趨勢，分別選取冰層上表面中心點A和Y軸四等分點B和X軸四等分點C觀測撓度變化曲線，冰層撓度測量點A，B及C如圖19 所示.

圖19 冰層撓度測量點Fig.19 Measuring point of level ice deflection

圓柱體水下上浮階段未與冰層接觸時A，B，C點的撓度變化曲線如圖20.可以看出A，B，C，3 點撓度變化趨勢及斜率基本一致，撓度變化曲線均出現負值，呈現震蕩后趨于穩定;A點撓度變化隨圓柱體上浮過程整體大于B和C兩點的撓度變化，說明水下上浮階段圓柱體運動過程中引起水上升擠壓冰面，導致圓柱體尚未與冰層接觸前發生變形從而產生撓度變化，且應力集中在冰面中心點;B和C兩點撓度變化曲線幾近吻合，說明水下上浮階段圓柱體對冰層的影響范圍以冰面中心點向四周擴散且逐漸衰減，與冰層放置于水面之上且四周約束的工況設定一致.

圖20 圓柱體水下上浮階段冰層各點撓度Fig.20 Deflection of each point of level ice during underwater floating of cylinder

由圖20 知，圓柱體出水破冰過程中冰層A點撓度隨上浮時間變化最為明顯，因此選取A點對比無水破冰和出水破冰時冰層的撓度變化.

圖21 為無水環境和有水環境下圓柱體上浮破冰過程中冰層A點處的撓度變化曲線.由圖21 可知兩條撓度變化曲線整體趨勢一致，隨著圓柱體逐漸上升擠壓冰層，冰層撓度逐漸增大;出水破冰過程冰層撓度變化峰值為1.48 mm，高于無水破冰時冰層撓度變化峰值0.81 mm;圓柱體突破冰層的時間也有明顯差異，有水環境下的冰層突破時間遠大于無水環境下的冰層突破時間;在2.5～ 2.58 s 間有一段平滑階段，由于結構物與冰層擠壓水形成的高壓力場，使得在圓柱體與冰層接觸之前冰層就存在初始撓度，即圓柱體在2.5～ 2.58 s 間未接觸到冰層.圖21 與圖18 曲線表現一致，均證明了有水環境下結構物-冰層耦合作用時存在水墊效應.

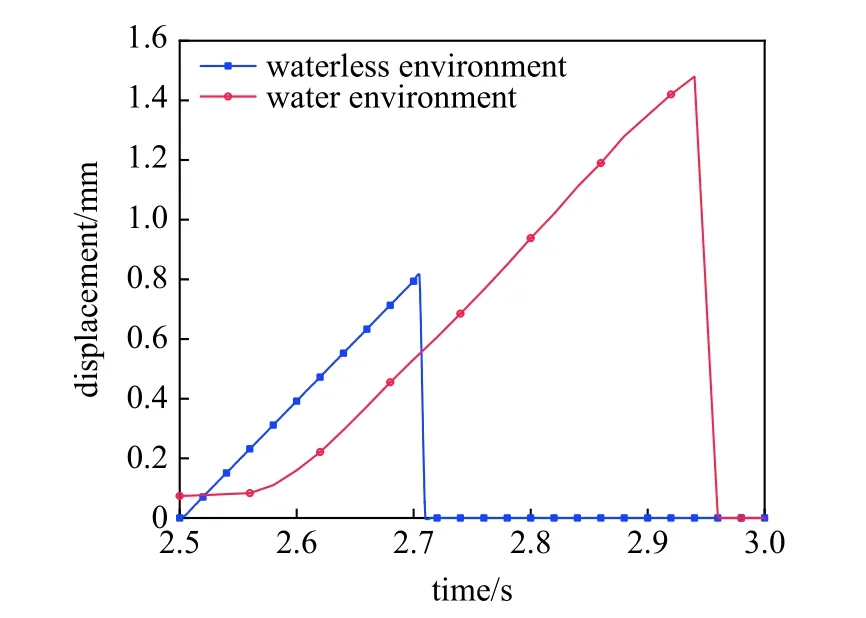
圖21 有水環境和無水環境下圓柱體上浮破冰過程中冰層A 點撓度變化Fig.21 Deflection change of point A of level ice in the process of cylinder floating and breaking ice in water environment and waterless environment

4.3 冰層應力響應及斷裂現象分析

圓柱體出水破冰過程中冰層未發生斷裂時von Mises 等效應力云圖如圖22.在圓柱體水下上浮階段，圓柱體運動排開水擠壓冰層，對冰層產生影響，應力主要集中于冰層中心即結構物正上方，但也存在應力并不集中的情況，由于結構物處于短暫加速狀態會使應力值不穩定，如圖22(a)到圖22(b)過程;在圓柱體處于勻速上升階段，應力完全集中在冰層中心，且冰層中心應力隨著結構物運動時間越來越大，如圖22(c)到圖22(d)過程.在結構物出水破冰階段，冰層應力極值點隨著圓柱體的運動迅速增大，當t=2.58 s 時結構物接觸冰層，應力極值為542.9 kPa，如圖22(e);當t=2.94 s 時結構物即將突破冰層，應力極值達到最大值，冰層突破應力為2509 kPa，如圖22(f).圓柱體出水破冰過程中的應力響應云圖與冰層撓度變化趨勢表現一致，無水環境下圓柱體突破冰層應力極值為2381 kPa，小于有水環境下冰層的突破應力極值.

圖22 冰層未發生斷裂時von Mises 等效應力云圖Fig.22 von Mises equivalent stress diagram when the level ice does not break

圖22 冰層未發生斷裂時von Mises 等效應力云圖 (續)Fig.22 von Mises equivalent stress diagram when the level ice does not break (continued)

圖23 為圓柱體出水破冰過程中冰層發生斷裂時的von Mises 等效應力云圖及破裂現象.圓柱體出水破冰過程中冰層斷裂現象大體上整體上與無水破冰相似，可以分為3 個階段.第1 階段，冰層受到圓柱體擠壓達到突破載荷超過冰的抗拉強度，浮冰板生成十字徑向裂紋，如圖23(a)所示，此時發生輕微卸載，徑向裂紋周圍的應力小于圓柱體的突破應力，隨著圓柱體運動十字徑向裂紋持續擴展，徑向裂紋周圍的應力也逐漸增大，如圖23(b)所示;第2 階段，冰層在出現十字徑向裂紋之后，隨著圓柱體繼續上浮，冰層上萌生更多徑向裂紋形成楔子，此時冰層仍未到達失效極限，如圖23(c)所示;第3 階段，隨著圓柱體繼續上升，達到冰層的失效極限，由于在冰層的上、下表面已經存在大量裂紋，圓柱體突破冰層造成冰層失效，部分碎冰在水浮力的作用下沿圓柱體堆積形成碎冰堆，如圖23(d)所示.

圖23 冰層發生斷裂時von Mises 等效應力云圖及現象Fig.23 von Mises equivalent stress diagram and phenomenon when level ice breaks

圖23 冰層發生斷裂時von Mises 等效應力云圖及現象(續)Fig.23 von Mises equivalent stress diagram and phenomenon when level ice breaks (continued)

5 結論

本文針對結構物與冰層相互作用強非線性問題，應用LS-DYNA 有限元軟件建立了基于S-ALE流固耦合方法及罰函數接觸算法的冰-水-結構物耦合作用數值模擬方法，研究了圓柱體垂直出水破冰過程，并對比分析了無水環境及有水環境下圓柱體垂直貫穿冰層破裂的共同點與區別，得到如下結論.

(1)通過冰梁結構4 點彎曲數值模擬，對比文獻中的試驗結果及數值模擬現象，驗證了彈塑性應變率材料的冰力學特性.進行了無水環境下圓柱體垂直貫穿冰層模型試驗及數值模擬，對比破冰載荷和冰層破裂現象，驗證了有限元方法研究結構物-冰層耦合作用問題的準確性.基于S-ALE 方法模擬了楔形體入水流固耦合過程，驗證了流固耦合算法的可行性.

(2)開展了圓柱體垂直出水破冰數值模擬，通過與無水破冰對比可知:有水環境下結構物-冰層間作用存在水墊效應.冰層突破載荷極值大小基本不會因有水環境或無水環境而產生明顯變化.由于水對冰層的支撐作用，有水環境下的結構物突破冰層的冰載荷持續時間顯著長于無水環境下冰載荷持續時間.

(3)描述了圓柱體垂直出水過程中的冰層斷裂現象，與無水破冰相比裂紋萌生到擴展現象相似，最終碎冰失效形式不同.無水環境下碎冰會迅速塌陷，而有水環境下的碎冰會沿圓柱體周圍堆積.有水環境下冰層彈性變形階段更長，撓度變化大于無水環境下的撓度變化.

綜上所述，由于在有水、無水環境下的結構物突破冰層冰載荷極值大小基本一致，研究冰層突破載荷極值及結構物強度相關問題時均可在無水環境下研究提高計算效率.而由于水墊效應的存在有水環境下結構物垂直出水貫穿冰層破裂過程與無水環境下結構物垂直貫穿冰層破裂過程存在明顯區別，需要根據研究目標選擇合適的數值模擬方法.