滾子修型及不同凸度值對滾動軸承接觸應力的影響

程 林，楊章林，江雪峰

(滁州職業技術學院 機械與汽車工程學院，安徽 滁州 239000)

自20 世紀60 年代以來，“邊緣效應”引起軸承過早疲勞失效的問題受到了各國學者的廣泛關注，并成為摩擦學研究的一個重要課題，即凸度設計[1].軸承滾子凸度設計包含2 大部分：合理的凸度量和有效的凸型.設計出合理的凸型是研究軸承滾子的靈魂所在.滾子凸型一般有5 種型式，即直線型、圓弧半凸型、圓弧全凸型、修正線型和對數型[2].Lundberg[3]最早給出了理論對數凸度方程，可使得滾子應力分布較為均勻，在工程應用中極為廣泛，但存在滾子端部不連續的缺點.Johns 等[4]改進了Lundberg 曲線端部不連續的缺點，提出了近似理論對數凸度方程，但改進后使得滾子很難獲得均勻的應力分布.Horng等[5]提出了圓弧凸型滾子的設計公式，對不同工況下圓弧凸型的參數選取進行了分析.馬家駒等[6]通過對Johns-Gohar 凸度方程增加1 個系數，提出了工程對數凸度方程，這種凸度設計方法可在一定程度上避免邊緣應力.Hiroki 等[7]優化了對數凸度方程，并引入3 個系數.但由于這3 個系數難以精確控制，因此該對數凸度方程沒有得到推廣應用.

本文主要研究2 種滾子凸型：直線型和相切圓弧修型母線.對同一模型的不同凸度值進行受力分析，并通過試驗驗證對滾子進行的凸度修型，能夠有效提高應力分布的均勻性，緩解應力集中現象，減少軸承磨損；給出工程實際加工中滾子相切圓弧修型母線時最合理的凸度范圍，可為圓柱滾子軸承的設計和實際生產提供參考.

1 滾子凸度修型方式

本文以圓柱滾子軸承KIRD234021-YA 型的滾子與內圈之間的接觸為例，分析不同修型時的應力分布情況.軸承的主要幾何參數如表1所示.

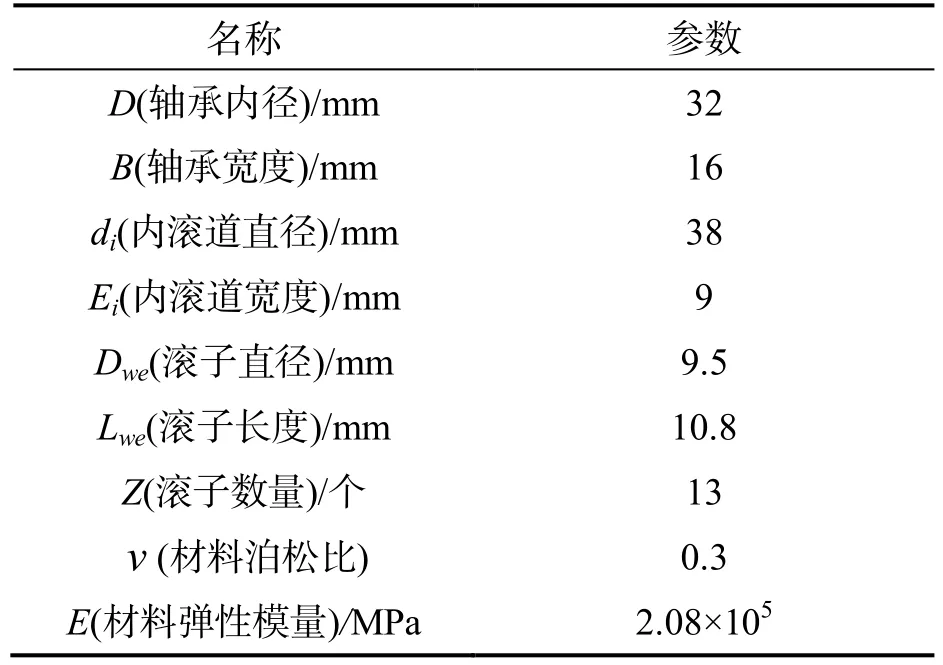
表1 KIRD234021-YA 軸承主要參數

滾子凸度大多為最常見的無凸度滾子(平頭滾子)，但是為了盡可能地降低應力集中，部分滾子在圓柱面與凸起部分用相切圓弧曲線來取代直線，就形成了相切圓弧修型母線.式(1)和式(2)分別為圖1(a)和圖1(b)所對應的不同修型滾子母線方程.其中，Dwe為滾子公稱直徑；Lwe為滾子有效長度(Lwe=l+2Rc對應圓弧長度)；l為平直段母線長度；Rc為圓弧修形的圓弧半徑[8].

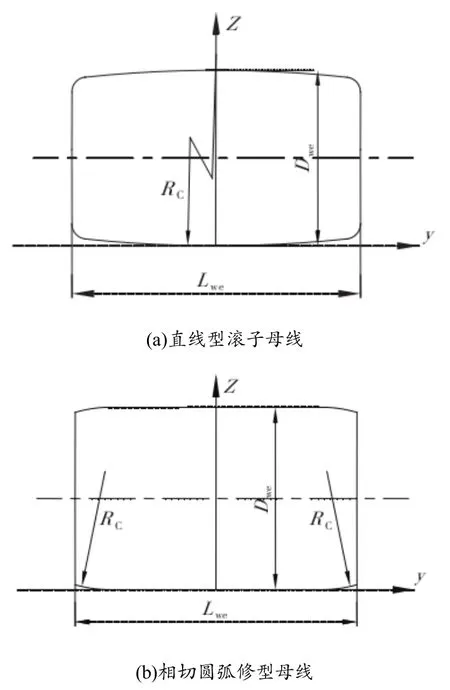
圖1 滾子凸度修型方式

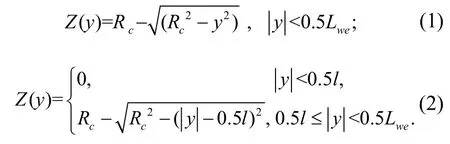
2 有限元仿真結果分析

2.1 有限元模型

圖2(a)和圖2(b)分別為滾子直線修型和滾子相切圓弧修型母線模型.2 個模型均采用CATIA軟件建模，導入Nastran 中的Sweep 模塊進行網格預處理，并對其模型進行六面體網格劃分，分別得到有限元模型節點數量278 443 和316 751，單元數量84 732 和88 725[9].

圖2 不同修型方式模型

2.2 滾子無凸度滾道接觸應力

圖3 為圓柱滾子軸承Romax 受載后的偏移模型[10].該結構為懸臂梁結構，其內圈盡可能按照圖紙尺寸建模，固定端用剛度軸承固定.從圖3中可看出，加載后軸承最大偏移量為52.65 μm.

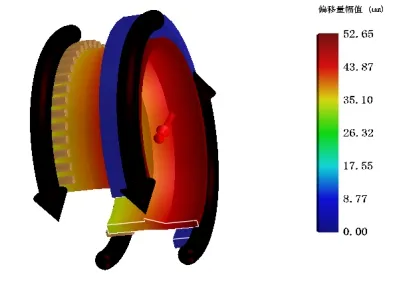
圖3 受載偏移模型

圖4 為滾子直線修型時內圈滾道接觸應力云圖.由圖4 可知，內圈滾道最大接觸應力值約為6 729 MPa，超過了材料熱處理后的許用接觸應力4 000 MPa.因此，軸承內圈滾道及滾子端部極易產生疲勞點蝕及剝落失效，且應力云圖顯示為非正常狀態.

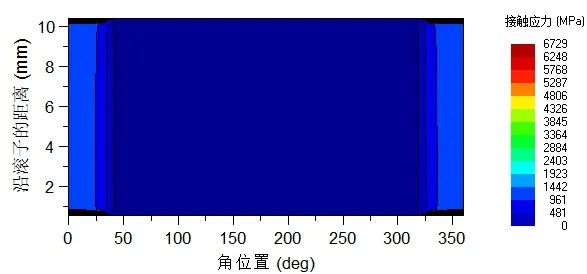
圖4 滾子無凸度應力云圖

2.3 滾子相切圓弧修型滾道接觸應力

圖5 為滾子相切圓弧修型不同凸度值時內圈滾道接觸應力云圖.圖5(a)為滾子凸度1 μm 時滾道應力云圖，由該圖可知，軸承滾道兩側的上邊緣有明顯的應力集中現象，且偏載現象也較為嚴重；圖5(b)為滾子凸度2 μm 時內圈滾道應力云圖，由該圖可知，滾道兩側存在少量的偏載現象，且最大應力值為1 397 MPa(遠低于材料熱處理后的許用應力值4 000 MPa)[11].

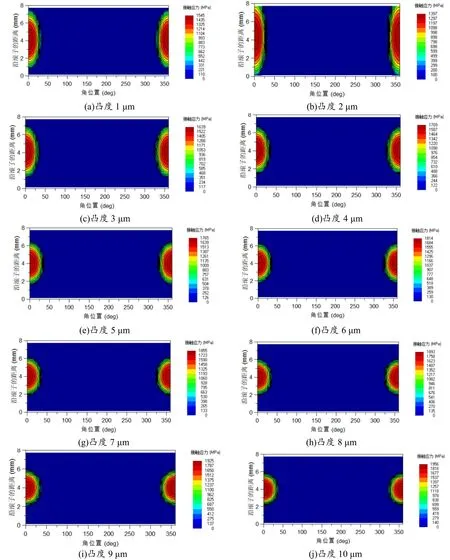
圖5 不同凸度值時內圈滾道接觸應力云圖

分別計算滾子未修型和相切圓弧修型時不同凸度值的內圈滾道應力值，其結果見表2(滾子的許用接觸應力值為4 000 MPa).

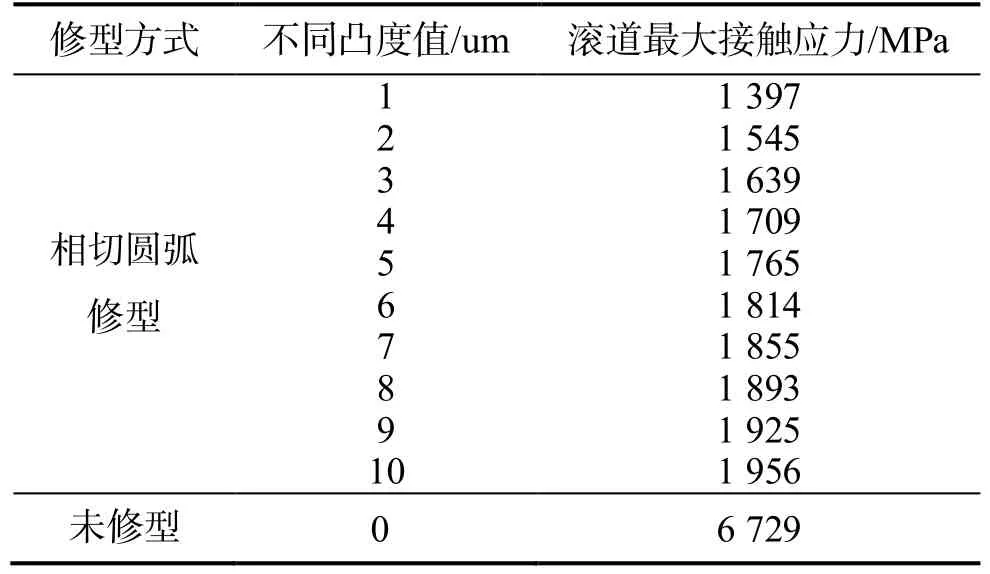
表2 不同凸度值時內圈滾道最大應力值

從圖5(a)～圖5(j)及表2 可知，對滾子進行凸度修型，確實能夠有效提高應力分布的均勻性，緩解應力集中現象；凸度值較小時內圈滾道最大接觸應力也較小，但偏載現象嚴重；凸度較大時偏載現象減小，但內圈滾道最大接觸應力有所增加.結合軸承加工工藝及承載能力考慮，較為合適的凸度范圍為3～8 μm.

3 滾子軸承疲勞壽命試驗

3.1 壽命試驗機

為驗證滾子修型能夠有效改善軸承應力分布的均勻性，緩解應力集中現象，進行疲勞壽命試驗對其進行驗證.所用疲勞壽命試驗機型號為ZS30-60，該試驗機可實時監測試驗軸承的溫度、轉速等常規試驗參數，同時還有高溫報警功能.當試驗溫度超過預定溫度時，試驗將被迫停止，起到高溫保護的作用[12].

3.2 試驗軸承

圖6 所示為試驗前軸承，共6 套，分別為滾子直線修型(無凸度)，滾子相切圓弧修型且修型凸度依次為1，3，5，8 和10 μm.

圖6 試驗前軸承

采用Castrol BOT 720LV9 潤滑油，在試驗載荷5 000 N，轉速4 000 r/min 的條件下，進行軸承疲勞壽命試驗，試驗軸承連續運轉273 h，超過軸承的1.5 倍額定壽命L10 后[13]，拆下軸承，發現軸承滾子較滾道磨損更為嚴重(見圖7).

圖7 為試驗后每套軸承磨損最為嚴重的滾子圖片.圖7(a)為試驗后凸度值為1 μm的滾子圖片，從圖中可看出滾子上端面有明顯的點蝕剝落，且滾子受載后出現明顯的偏載現象，其結果與軸承仿真結果相吻合.

圖7(b)、圖7(c)和圖7(d)分別為試驗后凸度值為3，5 和8 μm 的滾子圖片.從中可以看出，實驗后凸度值為3，5 和8 μm 的滾子兩端及中部無明顯磨損，滾子表面也較為光亮，這與內圈滾道仿真結果相吻合.

圖7(e)和圖7(f)所示為試驗后凸度值為10 μm和無凸度的滾子圖片.從圖7(e)中可看出，試驗后凸度值為10 μm 的滾子上端面存在點蝕，且點蝕現象較為嚴重；從圖7(f)可看出，試驗后滾子上端面存在大面積的剝落現象，且軸承受載后出現了嚴重的偏載現象.這與內圈滾道的仿真結果相吻合.以上結論驗證了對滾子進行凸度修型，能夠有效提高應力分布的均勻性，緩解應力集中現象，減少軸承的磨損，延長軸承使用壽命[14].

圖7 不同凸度值滾子最大磨損量

4 結論

1)凸度值為1 μm 的滾子上端面有明顯的點蝕剝落，且滾子受載后出現明顯的偏載現象.

2)凸度值為3，5 和8 μm 的滾子兩端及中部無明顯磨損，滾子表面也較為光亮.

3)凸度值為10 μm 的滾子點蝕現象較為嚴重，無凸度修型滾子存在大面積的剝落現象，且軸承受載后出現嚴重的偏載現象.

4)對滾子進行凸度修型，能有效提高應力分布的均勻性，緩解應力集中，減少軸承磨損，延長軸承使用壽命.