基于變量重要性和偏最小二乘的近紅外特征篩選方法研究

黃 新，劉偉平

(湖南城市學院 a.管理學院，b.圖書館，湖南 益陽 413000)

近紅外光譜是一種簡單、快速、無破壞性的新型綠色分析檢測技術，被廣泛應用于食品檢測、環境保護、石油化工以及中藥光譜分析等領域[1].近紅外光譜數據分析的困難在于波長變量之間通常存在嚴重的多重共線性，同時含有大量無信息波長甚至是噪聲波長，如果直接對全光譜進行建模分析不僅會增加模型的復雜程度與計算代價，甚至還會降低模型的預測性能.因此，光譜變量選擇已經成為近紅外光譜數據分析中一個關鍵的環節，對提高模型的預測能力和穩健性具有重要的意義.

目前，為了提高模型的預測能力，國內外學者們提出了一系列基于PLS的變量篩選方法.其中有代表性的方法有：無用信息刪除(uninformative variable elimination，UVE)[2-3]；移動窗口偏最小二乘(moving window partial least squares，MWPLS)[4]；自適應競爭權值采樣(the competitive adaptive reweighted sampling method)[5-6]等.

為進一步提高變量選擇結果的穩健性，本文將變量重要性融入到PLS 中，提出了一種新的基于變量重要性的偏最小二乘特征變量篩選方法(VISPLS)，它是基于變量重要性的向前變量選擇算法.同時，選擇斯皮爾曼(Spearman)相關系數、肯德爾(Kendall)相關系數、選擇性比(selectivity ratio,SR)、投影變量重要性(variable importance in projection VIP)來度量變量的重要性，并用2 個真實的近紅外光譜數據集來評估VISPLS 的性能，旨在提高系統預測性能.

1 偏最小二乘原理與算法步驟

偏最小二乘(partial least squares,PLS)法融合了多元線性回歸分析、主成分分析和典型相關分析3 種分析方法，由Wold 引入化學計量學，成為近紅外數據分析的主要方法[7].給定1 個n×p自變量矩陣X，每行代表1 個樣本，每列表示1個變量.則n×q因變量矩陣Y可記為

X=(x1,x2,…,xn)T,Y=(y1,y2,…,yq)T.

其中,xi（i=1,2,…,n）是1 個p維的列向量；y j（j=1,2,…,q）是1 個n維的列向量；T表示向量或矩陣的轉置.

偏最小二乘首先運用主成分分析和典型相關分析方法，分別在數據X和Y中提取主成分t1和u1，t1和u1應滿足下列2 個條件：

1)t1和u1應該盡可能多地包含原始數據矩陣中的信息；

2)t1和u1之間的相關程度應該盡可能最大.

得到第1 個主成分t1和u1后，偏最小二乘再結合多元線性回歸分析方法，分別執行X對t1和Y對t1的回歸.若方程已經滿足精度要求，則算法停止；否則，繼續利用X被t1解釋后的殘余信息及Y被t1解釋后的殘余信息進行第2 成分的提取，如此進行，直到達到滿意的精度為止.

Wold[8]提出的非線性迭代偏最小二乘算法(nonlinear iterative partial least squares，NIPALS)是實現偏最小二乘回歸的基本方法.在此基礎上，目前有多種算法能夠實現偏最小二乘回歸.下面采用Lewi[9]在1995 年提出的算法.

1)從矩陣Y中任選1 列，用u表示；

2)令w=XTu；

3)v=Xw，；

4)c=YTv；

5)u=Yc，；

6)重復步驟2)～步驟5)，直到收斂；

7)計算殘差矩陣，X←X-vvTX，Y←Y-vvTY.

PLS 回歸是一個迭代的過程，即提取第一個主成分后，按步驟7)計算殘差矩陣，然后應用殘差矩陣代替原來的數據矩陣，算法重新開始，直到達到原始矩陣X的秩r.為避免過擬合，一般采用交互檢驗來確定最優的主成分數.在提取r個主成分后，能夠得到n×r矩陣V和U，p×r矩陣W和q×r矩陣C，它們的列分別由構成.這樣，PLS回歸模型就能夠寫成矩陣形式

Y=XB+E.

其中，E是殘差矩陣.這個方程和通常的嶺回歸、多元線性回歸和主成分回歸模型有一樣的形式.然而，比較這些模型，矩陣B有以下形式：

B=W(PTW)-1CT.

其中，W=XTU；P=XTV(VTV)-1；C=YTV(VTV)-1.

利用矩陣V列的正交性，矩陣B又可寫成

B=XTU(VTXXTU)-1VTY.

2 4 種基于相關性的變量重要性

2.1 斯皮爾曼(Spearman)相關系數

Spearman 相關系數又稱秩相關系數[10]，是利用2 個變量的秩次大小作線性相關分析，對原始變量的分布不作要求，屬于非參數統計方法.設X=(x1,x2,…,xn)，Y=(y1,y2,…,yn)，將x1,x2,…,xn和y1,y2,…,yn按照升序進行排列，則X與Y的Spearman 相關系數為

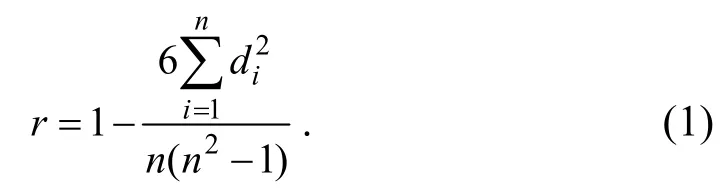
2.2 肯德爾(Kendall)相關系數

肯德爾(Kendall)相關系數又稱一致性系數[11]，是表示多列等級變量相關程度的一種方法.X與Y存在組元素對(xi,yj)，i≠j,i≥1,j≤n.Kendall 相關系數為

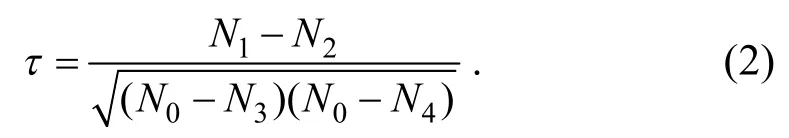
其中，N0是元素對總數；1N為X與Y正相關的元素對總數；N2為X與Y負相關的元素對總數；N3為X中相同元素對(xi=xj)總數；N4為Y中相同元素對(yi=yj)總數.

2.3 選擇性比(selectivity ratio,SR)

基于PLS,Kvalheim[12]提出了變量選擇性比(selectivity ratio,SR)的方法用于變量選擇.此法原理簡單，它認為被模型解釋得越多的變量越重要.建立PLS 模型后，可以得到每個變量被模型所解釋的方差和未被解釋的方差.在給定PLS的回歸系數b的條件下，有

其中，Si,exp為第i個變量的解釋方差；Si,res為第i個變量的殘差方差.

2.4 投影變量重要性(variable importance in projection，VIP)

Favilla 等提出了 variable importance in projection(VIP)[13]，其中第j個變量的VIP值為

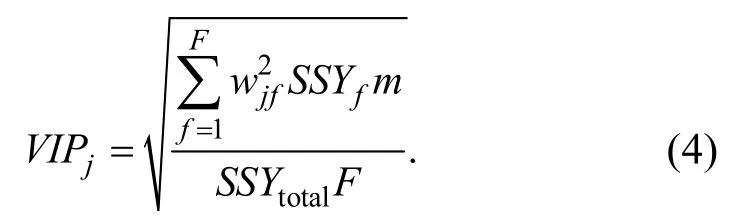
其中，wjf是主成分數f下第j個變量的權重值；SSYf是主成分數f的解釋方差平方和；m是變量個數；SSYtotal是因變量的平方總和.

3 基于變量重要性的偏最小二乘特征變量篩選方法(VISPLS)

針對近紅外光譜數據的特點，選擇常用的斯皮爾曼(Spearman)相關系數、肯德爾(Kendall)相關系數、選擇性比(selectivity ratio,SR)、投影變量重要性(variable importance in projection，VIP)來度量變量的重要性，利用變量的重要性和PLS 來篩選波長變量.VISPLS 是基于相關變量重要性的向前變量選擇算法.VISPLS 算法步驟如下：

1)標準化近紅外光譜數據矩陣X和Y.令M=｛x1,x2,…,xp｝表示整個變量集.

2)按照式(1)～式(4)分別計算相關變量的重要性，并按數值的絕對值大小順序排序；依次挑選系數最大時所對應的1 個變量，建立PLS 回歸模型；然后記錄均方根誤差(RMSE).這樣就得到P個PLS 回歸模型和P個RMSE值.

3)選擇P個RMSE值中最小值所對應的變量集，在這個變量集上建立最優的PLS模型.RMSE的計算公式為

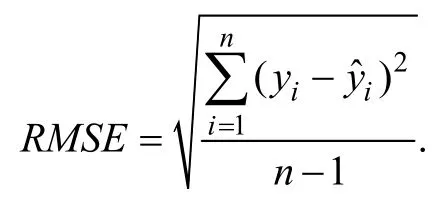
其中，yi和分別表示第i個樣本的實際值和預測值[14].

4 數據與結果討論

選擇2 個真實的近紅外光譜數據來評估VISPLS 算法的性能.RMSEOPT表示優化集的均方根誤差，RMSETEST表示測試集的預測均方根誤差，nLV表示PLS 模型的成分數，nVar表示VISPLS模型選擇的變量數，Threshold表示最優模型對應的閾值.基于斯皮爾曼相關系數、肯德爾相關系數、選擇性比、投影變量重要性的4 種偏最小二乘特征變量篩選方法分別記為：SpearmanPLS，KendallPLS，SRPLS 和VIPPLS.VISPLS 算法代碼是基于R 語言(版本4.1)編寫.

4.1 Corn 數據

Corn 數據有80 個樣本，波長為1 100～2 498 nm，并以間隔2 nm 取值，這樣總共有700 個變量[5].這80 個樣本是運用“m5spec”，“mp”和“m6spec”3 種不同的近紅外光譜儀測量得到的.在本研究中，只應用預測矩陣“m5spec”與油量(oil)因變量來評估VISPLS 算法.圖1 是數據集Corn的光譜圖.Corn 數據的80 個樣本被隨機地分成訓練集(train set,40)、優化集(optimization set,20)和測試集(test set,20).

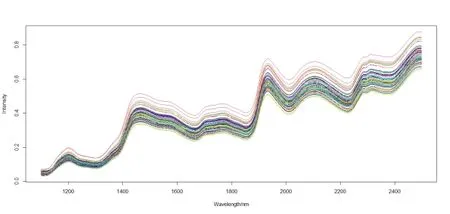
圖1 數據集Corn 的光譜圖

比較 VIPPLS，SRPLS，KendallPLS 和SpearmanPLS 4 種方法，VIPPLS 的預測精度是最好的，見表1.4 種方法選擇的的變量與波長區間分別列于圖2.由圖2 可知，基于變量重要性篩選變量能夠提高PLS 模型的預測性能.

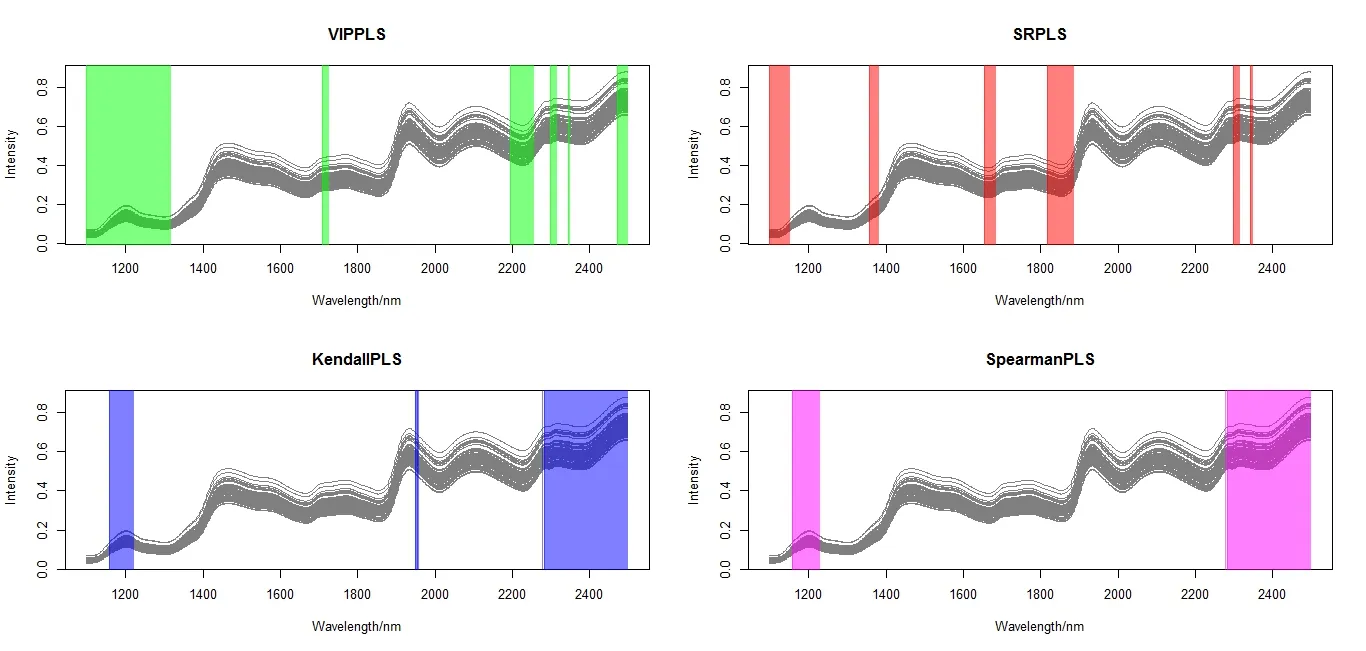
圖2 Corn 數據集上4 種方法選擇的波長變量

4.2 Gasoline 數據

Gasoline 數據[15]是另一個近紅外光譜數據集，它包含60 個樣本，近紅外譜是根據漫反射度的函數log(1/R)從900～1 700 nm中以2 nm為間隔測量出來的，共有401 個變量或波長(wavelengths)(見圖3).

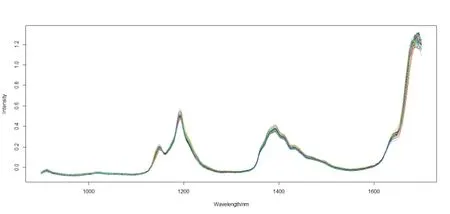
圖3 數據集Gasoline 的光譜圖

Gasoline數據的60 個樣本被隨機地分成訓練集(train set,30)、優化集(optimization set,15)和測試集(test set,15).

比較表2 中4 種方法可知，VIPPLS 取得了最好的預測精度.VIPPLS，SRPLS，KendallPLS和SpearmanPLS 4 種方法選擇的的變量與波長區間見圖4.

表2 數據集 Gasoline 的預測結果

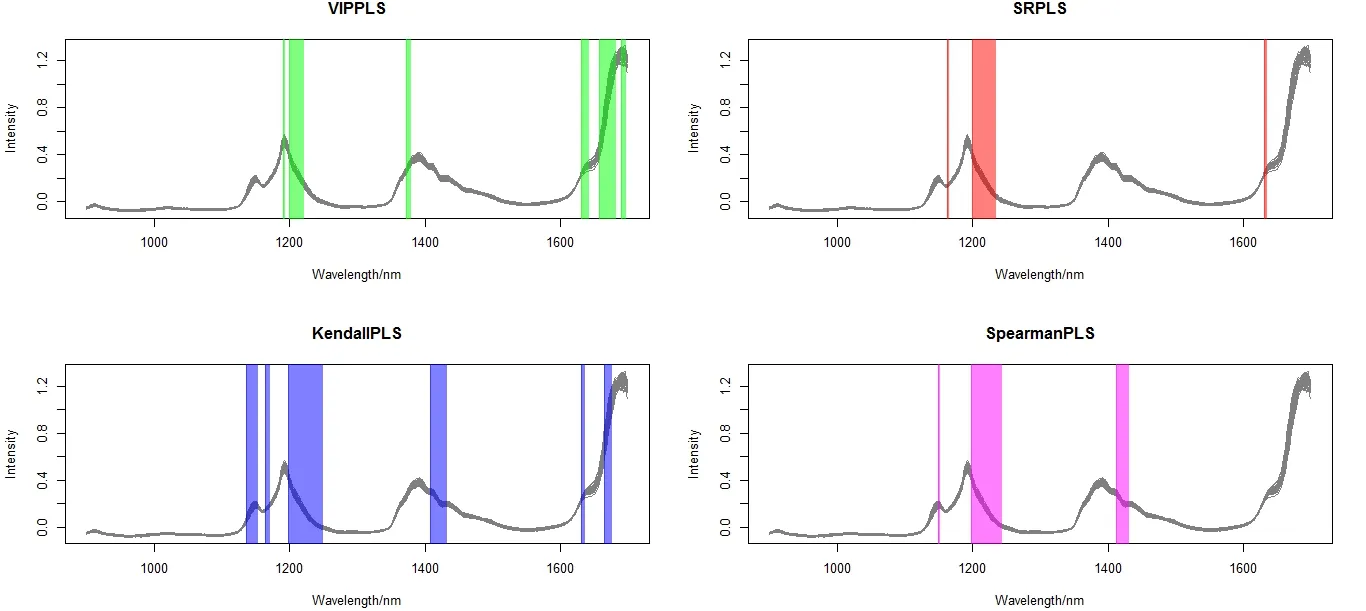
圖4 Gasoline 數據上4 種方法選擇的波長變量

5 結論

近紅外光譜數據通常包含成百上千個變量，變量數遠遠大于樣本數，研究者普遍認為，通過選擇有信息的變量或者刪除無用的變量后，建立的模型能夠明顯地提高模型的穩健性和預測精度.如何從這些數據中選擇重要的光譜變量是近紅外光譜建模的關鍵問題.本文將變量重要性融入到偏最小二乘回歸中，提出了一種新的基于變量重要性的偏最小二乘特征變量篩選方法VISPLS.選擇Spearman 相關系數、Kendall 相關系數、SR 系數和VIP 系數4 個指標來度量近紅外光譜變量的重要性，然后對變量重要性進行排序，再運用PLS 進行變量篩選.VISPLS 是一種基于變量重要性的前向迭代算法，通過2 個真實的近紅外光譜數據研究表明，VISPLS 可以更好地挖掘變量間的相互關系，能夠有效提高近紅外光譜模型預測性能.