Shearlet域基于非局部均值的地震信號去噪

李 民，周亞同，李夢瑤，翁麗源

(河北工業大學 電子信息工程學院，天津 300401)

地震信號可用于勘察地下結構，是進行油氣資源獲取的重要前期工作之一[1]。但在野外進行地震勘探時受地表環境復雜性影響或儀器性能限制導致采集到的地震信號往往存在噪聲，信噪比較低。如果不對這些信號去噪勢必會影響后續的處理，不利于真實反映地質結構信息[2-3]。針對地震信號去噪，國內外學者提出了不同的去噪方法，按處理領域大致可分為兩大類：一是空間域基于濾波的去噪算法，包括均值濾波、中值濾波、維納濾波等。二是變換域的去噪算法，包括傅里葉變換、小波變換[4]、Radon變換等。

當前地震信號去噪算法中多尺度幾何分析受到廣泛關注，常用的多尺度幾何分析方法包括Curvelet變換[5]、Contourlet變換[6]和Ridgelet變換[7]，均已成功應用于地震信號去噪并取得良好的效果。2007年，Guo等[8]根據緊支撐框架構造理論，經過嚴密的數學邏輯推導得到了Shearlet變換，它克服了小波變換的局限性，有更好的方向靈敏度，更稀疏的表示性能，并且能夠捕捉地震信號的內在幾何特征。但傳統的Shearlet變換不具有平移不變性，導致去噪后會出現偽吉布斯現象。為解決這一問題，非下采樣Shearlet變換(NSST， nonsubsampled shearlet transform)應運而生，取消了傳統Shearlet變換的下采樣操作，使其不僅有更好的方向敏感性和最優稀疏表示性能，還具有平移不變性，克服了偽吉布斯現象，極大地推動了多尺度幾何分析工具的發展。

近年來，基于Shearlet變換的地震數據處理方法相繼提出，傳統的閾值處理方法是對變換域所有系數使用統一閾值，但基于傳統閾值處理方法的Shearlet變換在地震信號去噪中存在局限性，因此童思友等[9]對閾值處理的方法進行了改進，提出了隨尺度和方向變化的自適應閾值。趙海濤[10]從變換的角度對其進行了改進，根據信號的方向和空間相關性提出了基于循環平移的Shearlet變換自適應閾值降噪算法。但由于Shearlet變換不具有平移不變性，而且對地震信號進行稀疏表示亦不是最優的，隨后提出的非下采樣Shearlet變換則解決了傳統Shearlet變換存在的問題，因此劉昕等[11]采用非下采樣Shearlet變換對地震信號進行噪聲壓制，結果表明該方法比小波變換的去噪能力更強。

非局部均值算法最初是用于數字圖像處理，能很大程度上減小振鈴效應，但傳統的NLM(non-local means)不能夠很好地衡量圖像細節和邊緣信息，會導致圖像失真，因此郭晨龍等[12]提出了帶有梯度信息的GSSIM(gradient structural similarity)算法，能較好地保存圖像邊緣和細節信息。王思濤等[13]則直接將邊緣檢測算法和NLM算法相結合，同樣可達到保存圖像邊緣信息的目的。但以上處理都是在時空域進行，Souidene等[14]根據小波系數服從廣義高斯分布，提出了基于廣義高斯模型的非局部均值算法，成功將NLM應用于小波域，直接對小波系數進行處理，去噪效果良好，但該算法只適用于小波變換一級分解，具有局限性。

考慮到Shearlet變換在高維空間比小波變換有更好的稀疏表示，且Shearlet系數也服從廣義高斯分布，因此文中考慮在Shearlet域使用NLM算法，并將之用于地震信號去噪。已知Shearlet變換之后的細節參數近似為廣義高斯分布[15]，在此基礎上對變換之后的細節系數進行NLM去噪，經過反變換得到去噪之后的地震信號。實驗表明去噪效果良好。

1 非下采樣Shearlet變換

1.1 傳統的Shearlet變換

Shearlet變換是復小波理論和多尺度幾何分析通過特殊形式的具有合成膨脹的仿射系統構成[16]，通過對基函數的縮放、剪切和平移等仿射變換來生成具有不同特征的Shearlet函數。當維數n=2時，Shearlet函數的具有合成膨脹的仿射系統定義為：

SAB(ψ)={ψl,m,n(x)=|detA|l/2ψ(BmAlx-n):l,m∈Z,n∈Z2}，

(1)

式中：ψ∈L2(R2)；l是尺度參數；m是剪切參數；n是平移參數。A和B都是2×2的可逆矩陣，且|detB|=1。A是各向異性膨脹矩陣，控制Shearlet變換的尺度，又稱為尺度矩陣，B是剪切矩陣，控制Shearlet變換的方向。對?a>0，b∈R，可得尺度矩陣A和剪切矩陣B為：

(2)

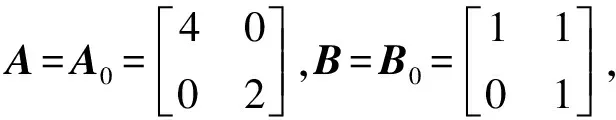
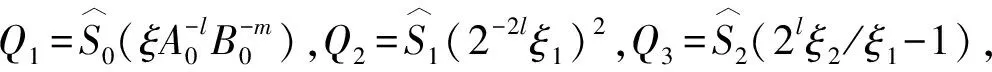
(3)

(4)

(5)

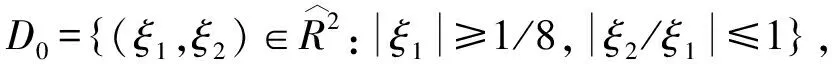
(6)

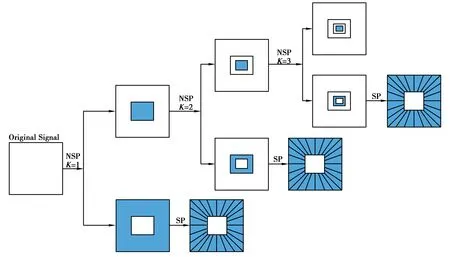
圖1 NSST的多尺度和多方向分解Fig. 1 The multi-scale and multi-directional decompositions of NSST

如果F={ψl,m,n(x):l,m∈Z,n∈Z2}表示Shearlet基函數，那么每個地震信號都可以用F表示出來，FN是最大Shearlet系數的近似值為：FN=∑〈F,ψl,m,n〉ψl,m,n，他們之間的關系式是：εN=‖F-FN‖=∑|〈F,ψl,m,n〉|2≤CN-2(logN)3， 隨著N項近似值的減小，基函數的代數和非常接近原始圖像的代數和。這表明Shearlet可以表示任何方向和任何尺度的圖像，而且與小波變換(CN-1)和傅里葉變換(CN-1/2)相比，Shearlet變換是最優的[17]。

1.2 非下采樣Shearlet變換

NSST是剪切變換的移位不變版本。 NSST與剪切變換的不同之處在于NSST取消了下采樣器和上采樣器，是一種完全移位不變的多尺度和多向擴展。NSST是由非下采樣拉普拉斯金字塔變換(NSLP)與剪切濾波器組合而成[18]。其中NSLP的分析可以通過迭代處理完成，為

(7)

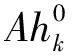
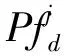
2 非局部均值算法

NLM算法在2005年由Baudes等[19]提出，該算法主要利用自然圖像中普遍存在的冗余信息進行去噪，利用了整幅圖像進行去噪，以圖像塊或者像素為單位在搜索框中尋找相似區域，再求平均，能夠較好地去除高斯噪聲[20-21]。若給定一個離散的噪聲圖像υ={υ(i)|i∈I}，估計值N[υ](i)可由圖像中所有像素的加權平均值計算得出：

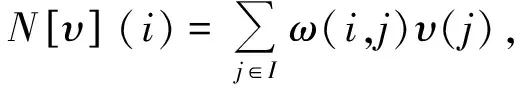
(8)

其中權重ω(i,j)取決于像素i和j相似度：

(9)

Z(i)是歸一化系數：

(10)

式中：h是平滑核寬度參數，控制平均范圍；y(i),y(j)表示的是鄰域窗口，大小通常為5×5,7×7,9×9，i,j表示的是鄰域窗口的中心像素點；Si是搜索窗口，其大小通常選為21×21。

文中提出的算法和經典NLM算法采用的鄰域窗口均為7×7，搜索窗口均為21×21。為保證有足夠多的相似度高的點，鄰域窗口選擇應遵循一定規律，過小會影響去噪效果，過大會增加算法時間復雜度，因此文中鄰域窗口大小設為7×7；搜索窗口同理，選取過小會導致失去地震信號的整體聯系，無法處理小范圍內隨機變化的點[22]，過大則會增加時間成本，因此，綜合考慮選擇搜索窗口的大小為21×21。

3 基于非下采樣Shearlet變換和非局部均值的地震信號去噪

近年來，多尺度幾何分析方法在地震信號去噪中受到廣泛關注，Shearlet變換作為多尺度幾何分析方法中的一種，已經成功應用于地震信號去噪與重建，并取得良好的效果[23]。NLM算法應用于地震信號去噪取得了良好的效果，但該算法經常直接用在時空域，而不能直接在變換域使用。針對這一問題，Souidene等[14]提出了基于廣義高斯模型的非局部均值算法，首次將非局部均值算法應用于小波變換域，但是這種方法有較大的局限性。因為小波變換只能反映信號的點奇異性，不能有效表示二維信號中具有多方向性的邊緣和紋理等幾何特性，即在高維情況下小波變換不是最優的表示方法，而隨后發展起來的Shearlet變換在高維情況有最優的稀疏表示，且Shearlet變換之后的系數亦滿足廣義高斯分布，因此考慮將Souidene提出的方法應用于Shearlet域，提出了Shearlet域基于廣義高斯模型的非局部均值算法。

該方法將廣義高斯分布和主成分分析(PCA, principal component analysis)引入Shearlet域的NLM算法中，首先將地震信號進行NSST分解，得到幾組Shearlet系數，由于Shearlet變換后的細節子帶系數近似為廣義高斯分布，可使用Souidene提出的方法估計尺度參數α和形狀參數β，然后將主成分分析方法應用于NLM的鄰域窗口和搜索窗口，得到其主成分進行下一步計算，提高運算速度。最后進行Shearlet逆變換得到去噪之后的地震信號。提出方法為：

(11)

其中：

(12)

式中：g(i)和g(j)是NLM中鄰域窗口的主成分，是式(9)和式(10)中y(i)和y(j)進行主成分分析之后的主成分，即g(i)和g(j)是y(i)和y(j)降維之后的表示[24]。當計算完成之后，根據式(8)來計算結果，即完成了對Shearlet系數的處理，并進行Shearlet逆變換即可得到去噪之后的地震信號。

3.1 參數估計

關于廣義高斯分布的參數估計方法有很多，通常采用標準差σ和絕對值的平均值E[|X|]的比值[25]：

(13)

式中：σ是Shearlet系數的標準差；E[|X|]代表Shearlet系數絕對值的平均值，可根據先驗信息設定形狀參數β的取值范圍，然后在范圍之內遍歷得到最優β值。代入式(14)即可得到尺度參數α，為

(14)

3.2 主成分分析

主成分分析是由Pearson提出，Hotelling加以發展的一種多變量統計方法，主要用于“降維”。所謂的“降維”，就是減少相關性的變量數目，用較少的變量(主成分)來取代原先的變量。通過主成分分析可以從復雜的關系中找到一些主成分，從而能更直觀地找到各變量的內在關系。一般來說，提取到的主成分與原始變量之間應滿足4個基本關系，即每一個主成分都是各原始變量的線性組合；主成分的數目遠遠小于原始變量的數目；主成分保留了原始變量絕大部分信息；各主成分之間互不相關。

主成分分析以方差最大理論為基礎，所謂的方差最大理論，是指從二維空間向一維空間轉換時需要找一個方向使得投影在該方向上的方差最大，即在此方向上關于原始變量的差異是最大的，差異越大，方差也就越大。

在文中，使用R表示地震信號中的所有點，r表示從R中隨機選取的點，即樣本，以y(i)為例，采用基于特征值分解協方差矩陣對其進行降維處理。具體步驟如下：

4)將特征值按照從大到小的順序排列，選其中非零的k個，將其對應的特征向量組成矩陣P，那么原矩陣轉換到新空間中，即g(i)=P×y(i)。

3.3 非下采樣Shearlet變換和非局部均值結合后用于地震信號去噪

Shearlet域基于非局部均值的地震信號去噪算法，首先將原始含噪信號進行非下采樣Shearlet變換得到Shearlet系數，然后對每個子帶計算其尺度參數α和形狀參數β，使用Souidene提出的基于廣義高斯模型的非局部均值算法對系數進行處理，得到去噪之后的系數，使用過程中對NLM算法用到的滑動窗口進行主成分分析以降低空間復雜度，最后通過Shearlet反變換得到去噪之后的地震信號。具體流程如圖2所示。

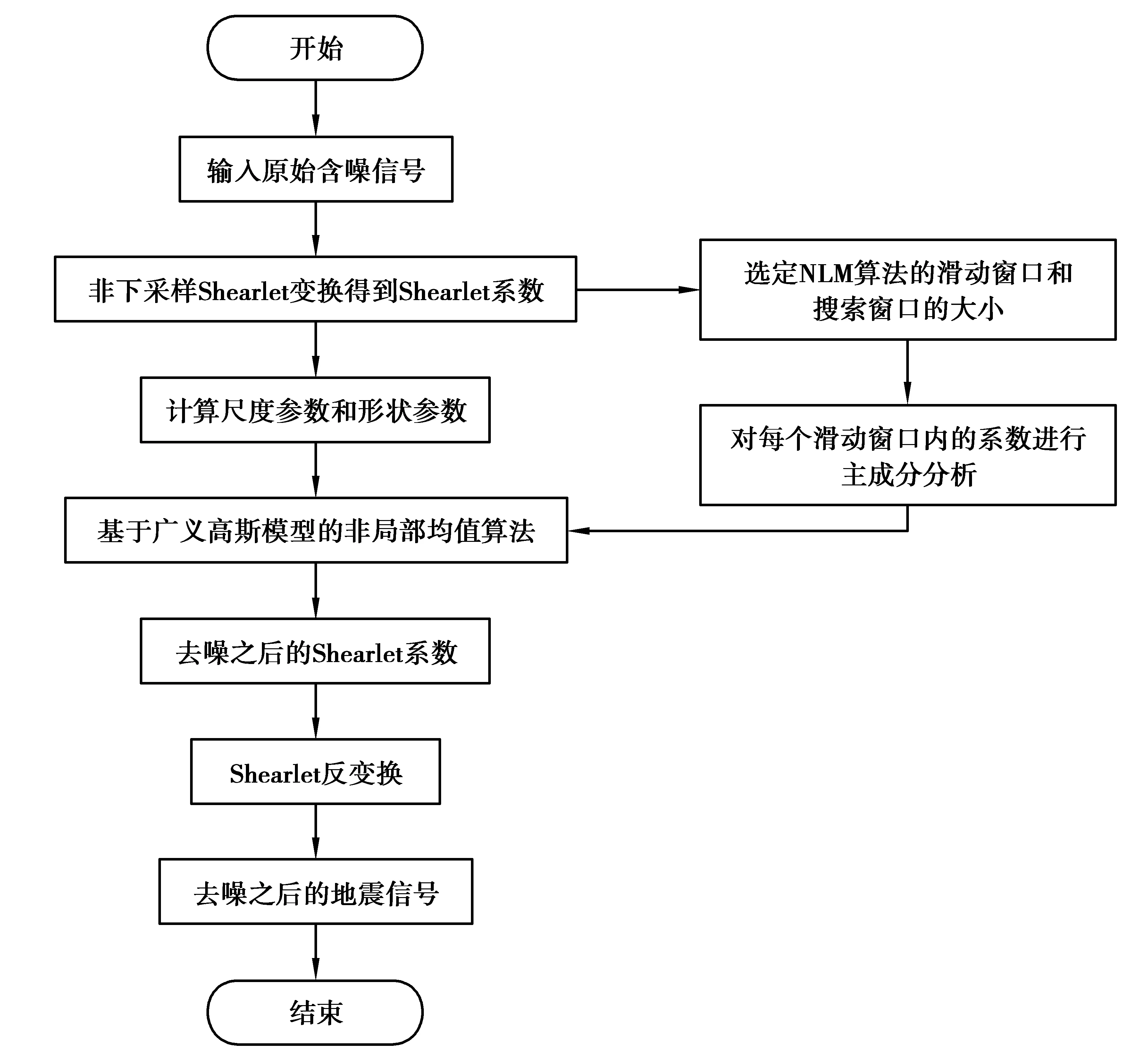
圖2 Shearlet域基于非局部均值的地震信號去噪算法流程圖Fig. 2 Flow chart of seismic signal denoising algorithm based on non-local mean in Shearlet domain

4 地震信號去噪實驗

去噪實驗在一臺戴爾筆記本上運行，處理器為i5-4200U，CPU為1.60 GHZ，內存為4 GB，64位操作系統，安裝有MATLAB-R2014b，地震信號去噪實驗中使用的算法都是通過多組實驗，反復調整參數，以去噪效果最優的參數組合進行對比實驗。通過峰值信噪比(peak signal-to-noise ratio，PSNR)、去噪均方誤差(mean squared error，LMSE)及結構相似度(structural similarity index，SSIM)等量化指標，比較Shearlet和NLM結合算法、Shearlet和硬閾值法結合、NLM算法以及Wiener濾波算法的性能。其中PSNR是使用最廣，最普遍的評價指標，在保證去噪之后視覺效果的前提下，希望越大越好；LMSE是反應估計量和被估計量之間差異程度的度量，希望越小越好；SSIM中c1=(0.01×L)2，c2=(0.03×L)2，L是采樣值的動態范圍，常用來衡量兩種圖像相似度，取值越接近1越好。

(15)

(16)

(17)

4.1 人工合成地震信號去噪

在實驗中，使用三級Shearlet分解，每一級分別包含3，4和4的剪切方向，每個級別內方向子帶數Ns=2s，因此，每一級分別包含的方向子帶數為8，16和16。圖3展示了人工合成地震信號近似系數和三級剪切變換細節系數。圖3(a)為人工合成地震信號，圖3(b)是原始地震信號的近似剪切系數，圖3(c)為第一級細節剪切系數，圖3(d)為第二級細節剪切系數，圖3(e)為第三級細節剪切系數。

圖3 剪切分解的示意圖Fig. 3 An illustration of shearlet decomposition

該人工合成信號共計104道，每道104個均勻采樣點，分別對該信號加方差為5%、10%、15%、20%的高斯白噪聲。為了使得文中算法和NLM算法都達到最優的去噪效果，需選取最優的平滑參數h，由于沒有嚴格的公式計算平滑參數h，因此需進行多次試驗，找到最優的平滑參數h之后，即可對人工合成地震信號進行去噪。圖4展示了文中算法和NLM算法在不同噪聲水平下PSNR隨平滑參數h的變化圖，其中圖4(a)是Shearlet和NLM結合算法在不同噪聲水平下PSNR隨平滑參數的變化圖，圖4(b)是NLM算法在不同噪聲水平下PSNR隨平滑參數h的變化圖。

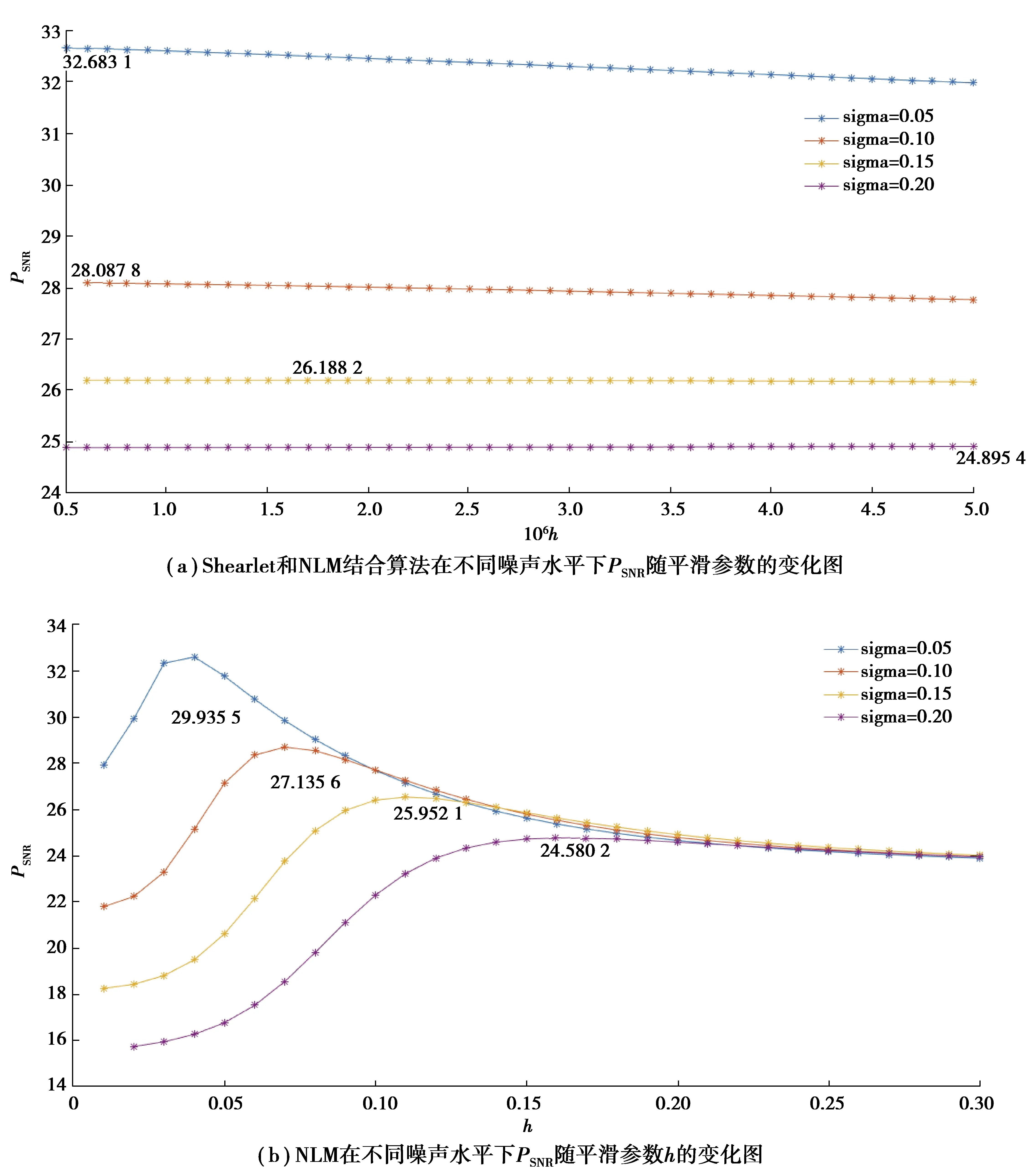
圖4 文中算法和NLM算法在不同噪聲水平下PSNR隨平滑參數h的變化圖Fig. 4 The variation of PSNR with smoothing parameters under different noise levels by proposed algorithm and NLM

對該地震信號添加噪聲方差為10%的高斯噪聲，原始人工合成地震信號如圖5(a)所示，圖5(b)是含噪地震信號，圖5(c)是NLM算法去噪結果，圖5(d)是硬閾值(hard threshold)法去噪結果，圖5(e)是Wiener濾波去噪結果，圖5(f)是文中算法去噪結果。

如圖5所示，4種去噪算法基本都能實現去噪任務，從去噪效果上來看，NLM算法的去噪結果還存在一些噪點，對細節部分的處理不如文中算法。硬閾值算法的PSNR雖然很高，但是由于硬閾值算法本身在進行去噪時過于絕對，不能夠自適應，所以硬閾值去噪算法丟失了大量的細節信息，導致效果圖過于平滑。Wiener濾波去噪結果還存在較大的噪聲，各方面都不如另外3種算法。綜合各方面考慮，文中算法去噪效果最佳。4種去噪算法的量化數據由表1給出。

圖5 人工合成地震信號去噪Fig. 5 Synthetic seismic signal denoising

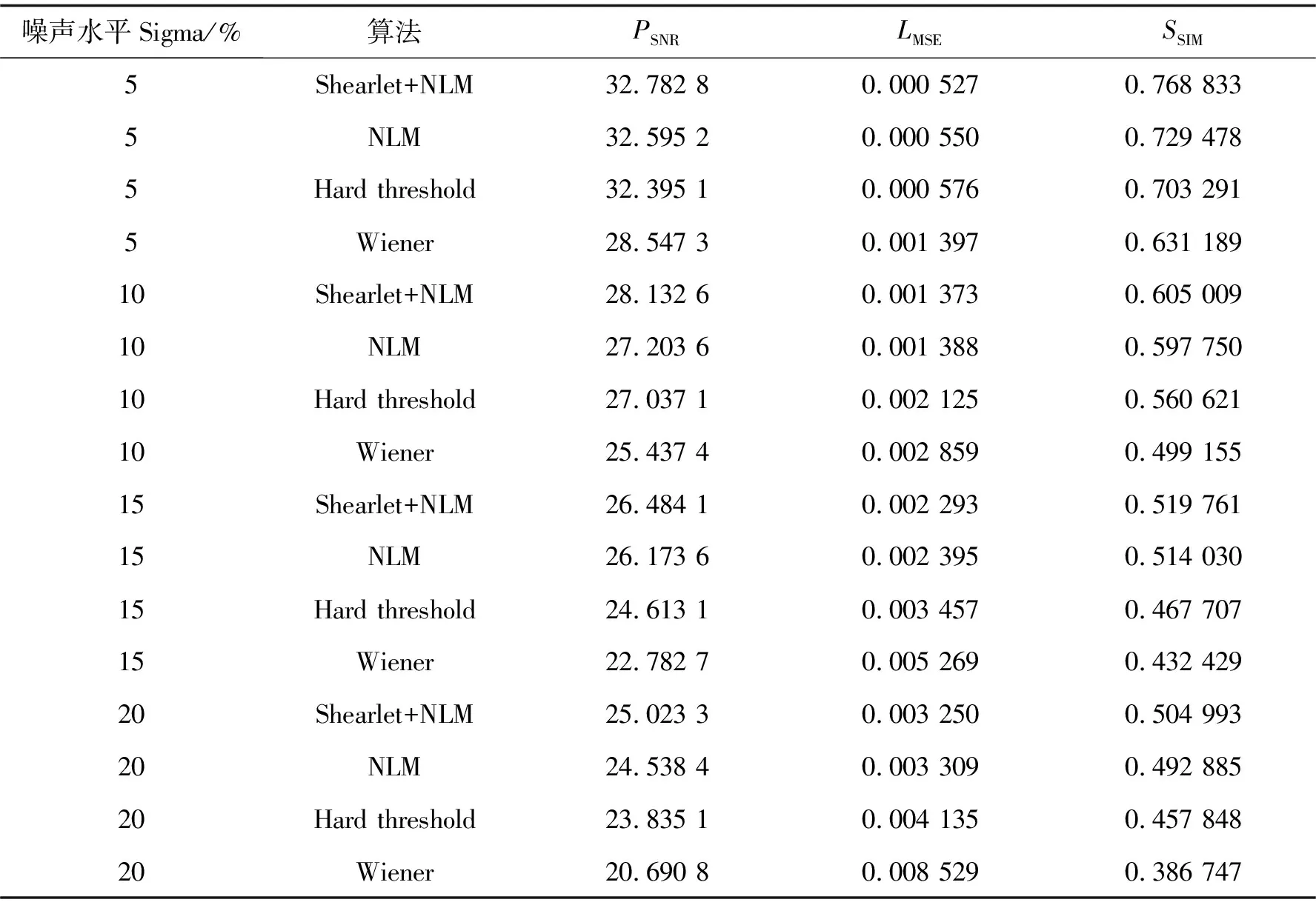
表1 各算法對人工合成地震信號去噪的性能(高斯噪聲)

從表1可以看出，對人工合成地震信號在噪聲水平為10%的時候NLM算法和硬閾值算法的去噪效果相差不大，但都比文中算法略差，Wiener濾波算法效果最差。從量化結果看，文中算法的PSNR的比NLM算法的PSNR高0.929，即提高了3.3%。因為NLM算法和硬閾值算法并不注重對細節部分的處理，導致去噪效果不理想，而文中算法對細節的處理更好，去噪效果更好。

4.2 海上地震信號去噪

該地震信號是野外海洋單炮數據Marshot3400.DAT中分割出的數據，共128道，每道128個采樣點。圖6展示了海洋地震信號近似系數和三級剪切變換細節系數的圖示。圖6(a)為海上地震信號，圖6(b)為海上地震信號近似剪切系數，圖6(c)為第一級細節剪切系數，圖6(d)為第二級細節剪切系數，圖6(e)為第三級細節剪切系數。分別對該信號加方差為5%、10%、15%、20%的高斯白噪聲，文中提出的算法中涉及一個平滑參數h，該參數沒有嚴格的計算公式，只能根據經驗選取，文中在一定范圍內進行實驗，選取最優的平滑參數h。圖7展示了Shearlet和NLM結合算法在不同噪聲水平下PSNR隨平滑參數h的變化圖。

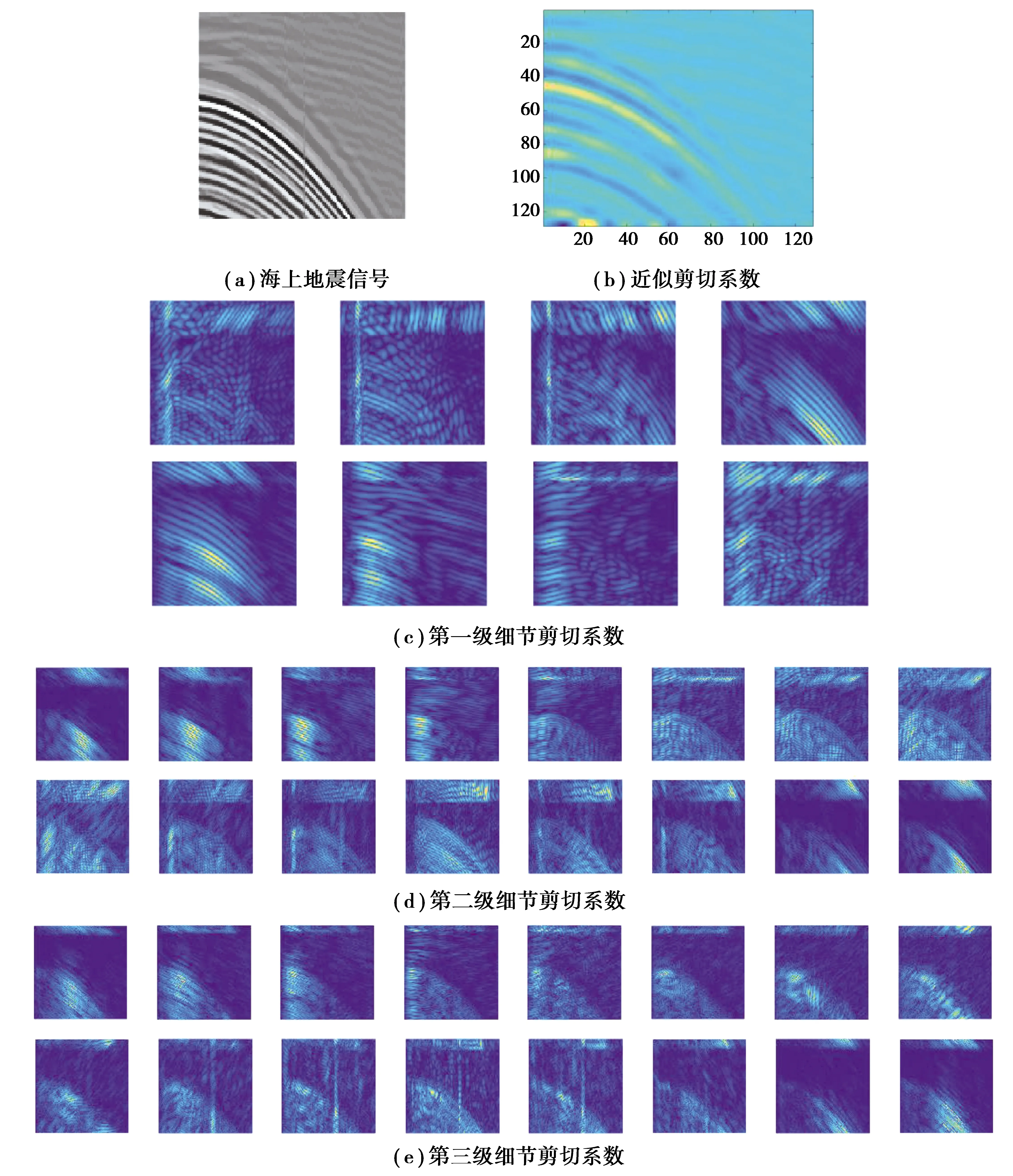
圖6 剪切分解的示意圖Fig. 6 An illustration of shearlet decomposition

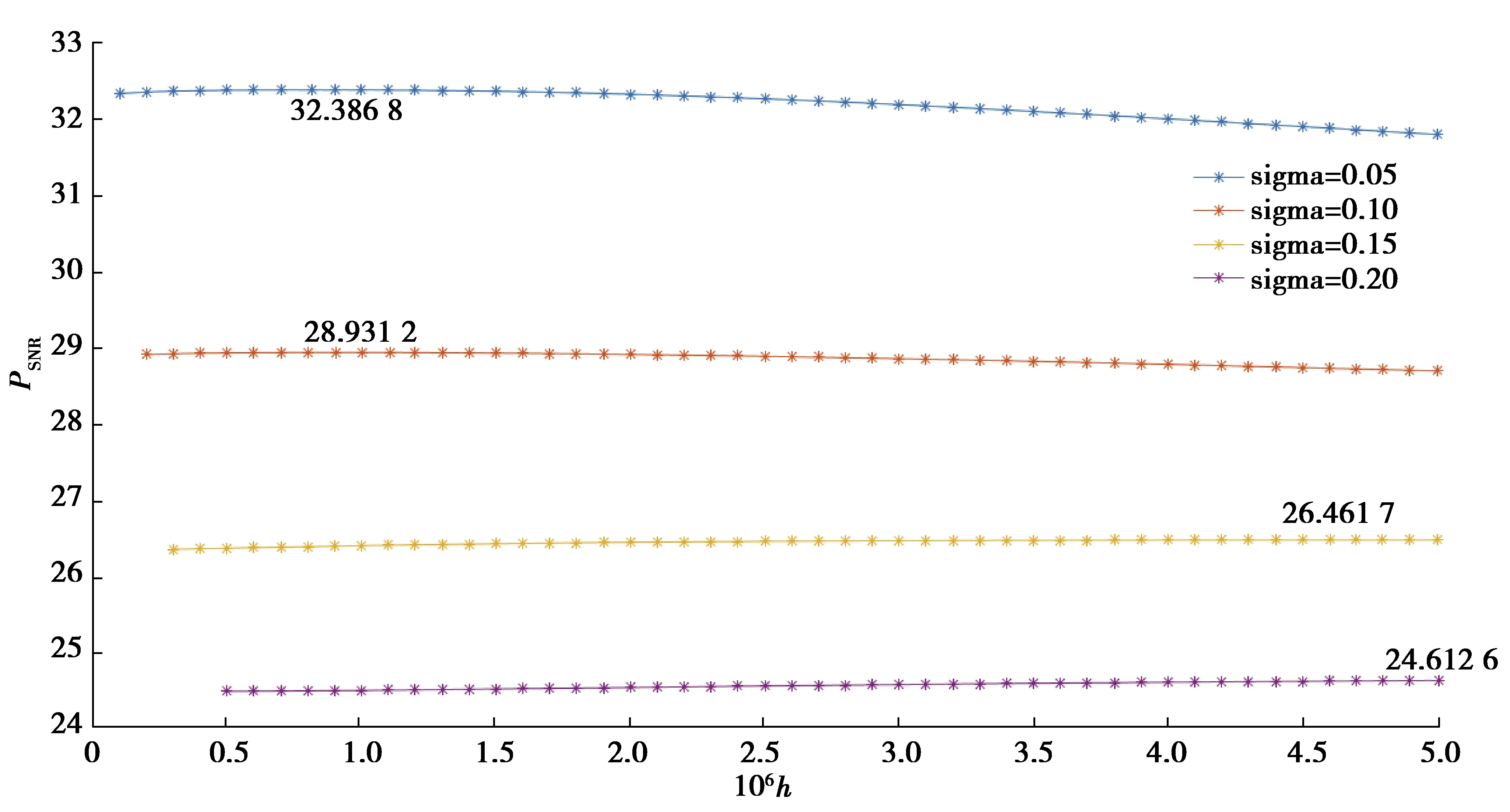
圖7 文中算法的PSNR隨平滑參數變化曲線圖Fig. 7 The variation of PSNR with smoothing parameters at different noise levels by proposed algorithm

NLM算法中平滑參數h按同樣方法選取其最優值，圖8展示了NLM算法在不同噪聲水平下PSNR隨平滑參數h的變化圖。

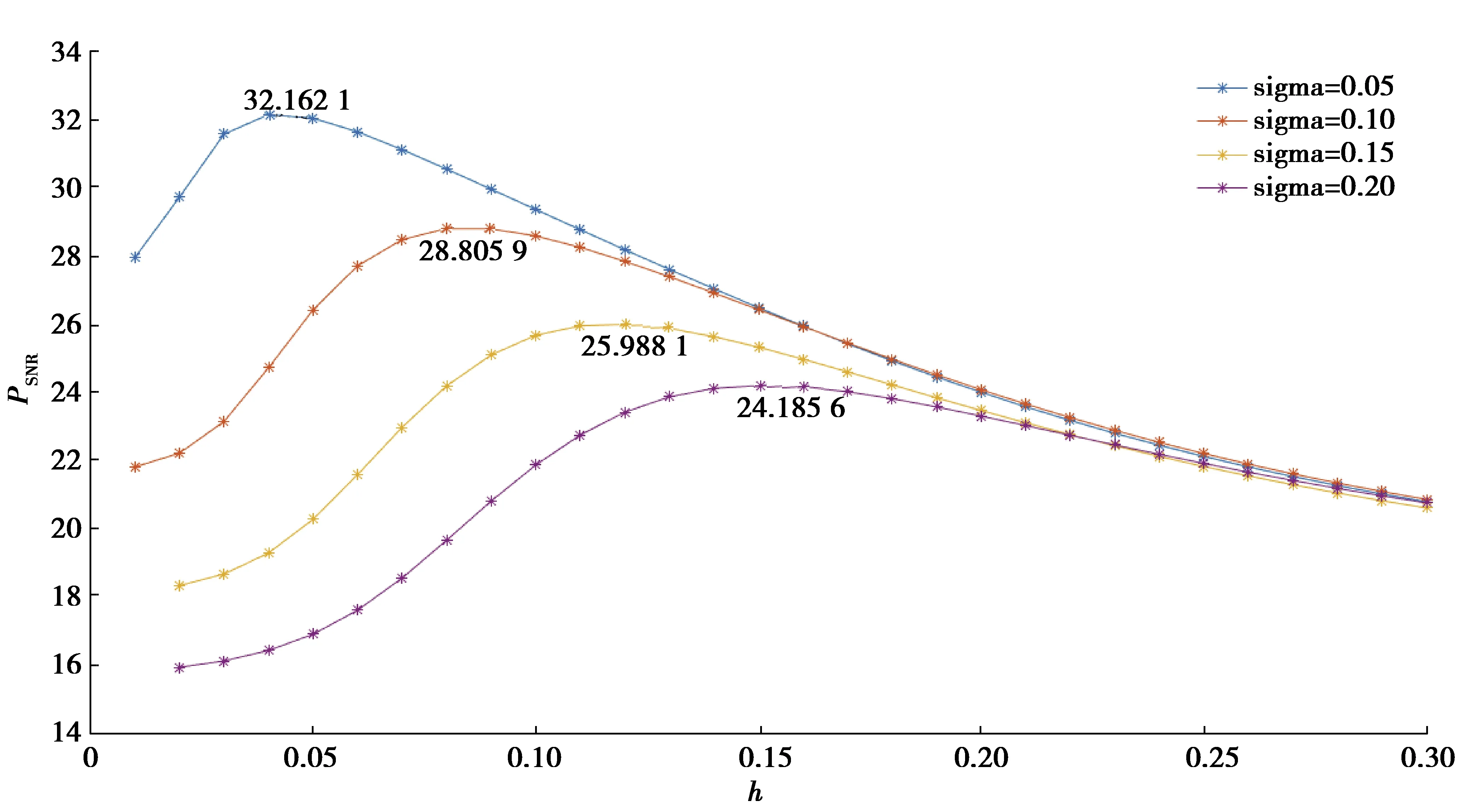
圖8 NLM算法的PSNR隨平滑參數變化曲線圖Fig. 8 The variation of PSNR with smoothing parameters at different noise levels by NLM algorithm

文中算法和對比算法平滑參數h均選擇使其去噪效果最優的值，通過對比圖7和圖8可以看到，以加方差為15%的高斯白噪聲為例，文中算法去噪效果最優的平滑參數h=0.51×10-5，NLM去噪效果最優的平滑參數h=0.12。

圖9展示了噪聲方差為15%，平滑參數均取最優值的情況下的去噪結果，圖9(a)是原始地震信號，圖9(b)是含噪地震信號，圖9(c)是NLM算法去噪結果，圖9(d)是硬閾值法去噪結果，圖9(e)是Wiener濾波去噪結果，圖9(f)是文中算法去噪結果。

如圖9所示，4種去噪算法基本都能實現去噪任務，比較4種去噪算法的性能，發現文中算法和NLM算法的PSNR比硬閾值算法更高，4種去噪算法的具體差異已量化比較，表2展示了4種去噪算法的去噪性能。

圖9 海洋地震信號去噪Fig. 9 Marine seismic signals denoising

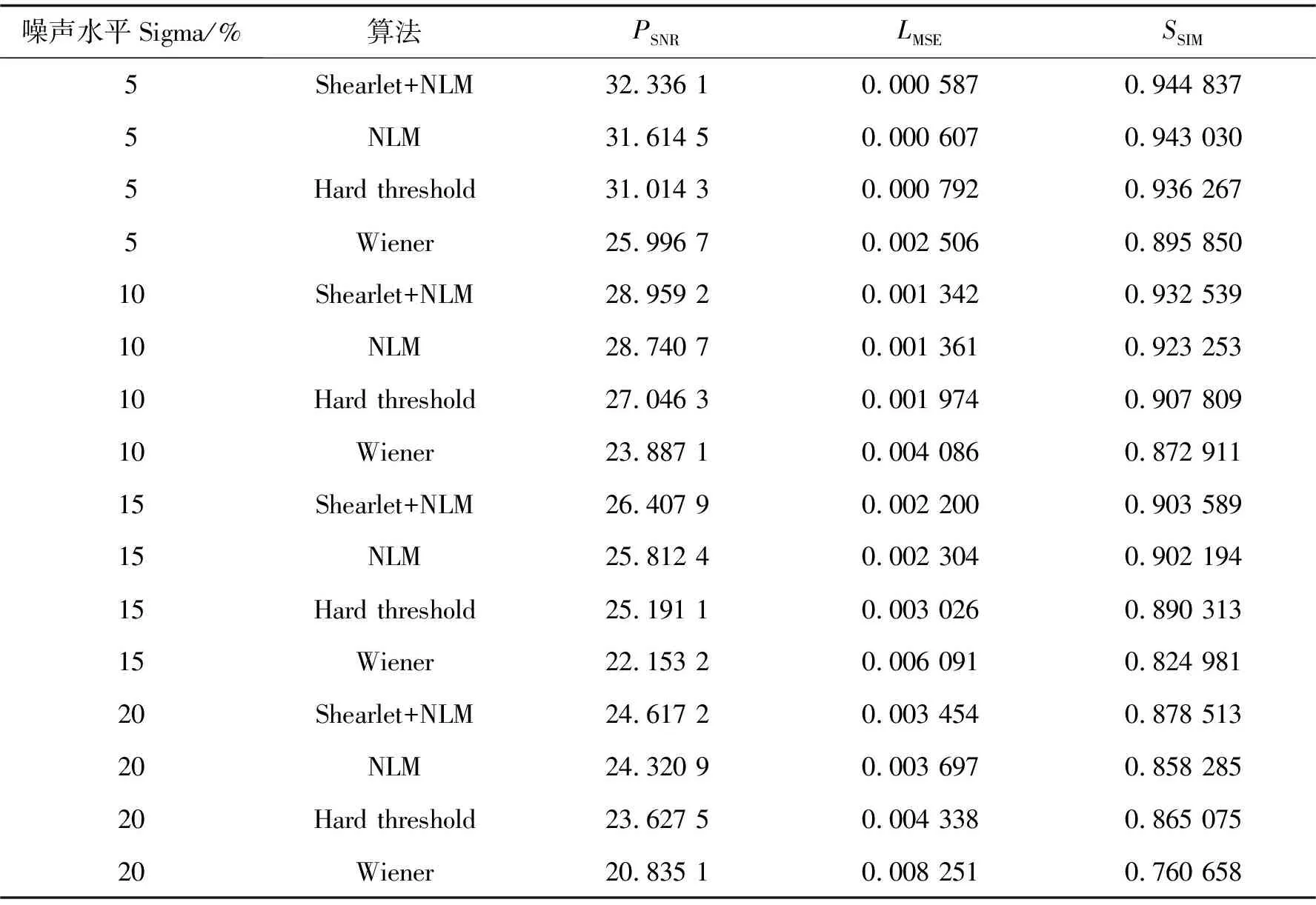
表2 各算法對海上地震信號去噪的性能(高斯噪聲)

表2可看出，在噪聲水平5%的情況下，文中算法和NLM算法的去噪性能相差不大，但比硬閾值法和Wiener濾波算法好，從具體量化結果來看，文中算法的PSNR為32.336 1，比NLM算法的PSNR多出0.721 6，即提高了2.23%。隨著噪聲水平的增加，文中算法更注重于細節處理所以仍能保持性能最佳，而NLM算法在噪聲水平逐漸增大的情況下，去噪效果逐漸不理想。硬閾值法去噪時會由于閾值設定問題導致去噪結果更平滑，丟失一些細節信息，從而導致去噪效果不理想。Wiener濾波算法對高斯噪聲有較強的抑制效果，但代價是容易失去地震信號的邊緣信息，導致去噪效果較差。

5 結 論

文中提出的算法利用非下采樣Shearlet變換后的細節系數近似為廣義高斯分布，結合NLM算法以及PCA對細節系數進行處理，再進行Shearlet逆變換得到去噪結果。將該算法應用于海洋地震信號和人工合成地震信號，與傳統的NLM算法、硬閾值法、Wiener濾波算法相比，文中算法對細節部分的處理更出色，NLM算法對含有更多相似塊的地震信號去噪效果更好，硬閾值算法對信號和噪聲區別較大的地震信號去噪效果更好，Wiener濾波算法對含有高斯噪聲的地震信號處理效果較好。就文中涉及的2種地震信號，文中算法能綜合考慮到細節部分和整體部分且無關噪聲種類，從而達到更好的去噪效果，因此采用Shearlet變換和NLM算法相結合對地震信號進行去噪更具優勢。