基于蒙特卡洛仿真的高空尾渦運動特性

魏志強，李曉晨

(中國民航大學空中交通管理學院，天津，300300)

飛機機翼在產生升力的過程中，上翼面及下翼面之間的壓強差將會導致在左右翼尖處形成轉向相反的翼尖渦流場[1]。當后方飛機不慎進入前機的尾渦流場時，可能會發生失速、滾轉、急劇俯仰等危險情況，嚴重威脅飛行安全[2]。近年來，空域繁忙程度的增加以及空域資源的日趨緊張使得充分利用高空資源越來越迫切，其中尾渦遭遇問題是高空飛行高度層垂直間隔縮減的重要限制因素。

空中交通流量的持續增長對空域利用效率提出更高要求。我國在8 900～12 500 m的平飛巡航高度區間內實施縮小最低垂直間隔(reduced vertical separation minimum, RVSM)，將飛行高度層之間的垂直間隔標準由600 m縮小到300 m，增加了空域容量。近年來，國際民航組織(international civil aviation organization，ICAO)開始著手研究在RVSM空域上擴高度層中實施縮小垂直間隔的可行性[3]，但尚未考慮飛機尾流的消散和運動對下方飛機飛行安全的影響問題。

目前針對尾渦流場參數的仿真計算在技術上可分為基于流體動力學方法的數值模擬技術和基于渦流演變機理的快速仿真計算技術。飛機尾渦流場的數值模擬主要包括大渦模擬、雷諾平均及分離渦模擬方法[4-6]。受計算機計算方法及運算能力的限制，在對飛機尾渦進行數值模擬時，有限的網格數量使得對尾渦形成階段的模擬較為清晰，但對于尾渦的消散和運動階段的數值模擬效果尚不夠理想。在尾渦流場參數的仿真計算方面，國外研究者通過建立數學模型描述尾渦消散機制。Holz?pfel等建立兩階段尾渦消散模型(two-phase wake vortex decay，D2P)來計算尾渦強度的衰減情況[7]。Sarpkaya等基于數值模擬數據的分析，認為尾渦的消散速率與雷諾數關系不大，而主要取決于大氣湍流度[8-9]。Proctor等建立了尾渦流場快速預測模型，并應用于終端區尾流仿真系統平臺。這些數學模型由于響應快速、運算高效、相對簡化而被廣泛應用于尾渦流場參數的仿真計算中[10-11]。

國內研究者主要致力于尾渦流場建模及尾渦參數計算方面的研究。魏志強等利用“天河一號”超級計算機進行數值模擬實驗，計算分析了不同側風下的渦量衰減、渦心速度等參數的變化情況[12]。沈淳等基于雷達探測反演方法預測飛機尾流行為及尾渦危險區域，為尾流動態安全間隔標準制定提供支撐[13]。谷潤平等建立多目標優化模型，以誘導滾轉力矩系數反映尾渦遭遇嚴重度，應用于飛機編隊飛行的前后機相對位置優化[14]。魏志強等分析了飛機加裝翼尖小翼后尾流安全間隔的變化情況，以及航空器重新分類時的尾流遭遇風險問題[15-16]。國內外研究者在尾渦流場參數仿真計算和安全間隔標準的制定方面開展的研究主要針對中低空及飛機的起降階段，未對12 500 m以上高空空域的尾渦流場特性進行分析。

為解決上述問題，文中首先建立了飛機尾渦物理模型。然后以某重型飛機為例分析12 500 m飛行高度以上的高空尾渦流場運動特性，根據蒙特卡洛方法仿真計算高空與中低空的尾渦下沉高度差異；最后分析高空尾渦渦核下沉運動的影響因素。研究結果為在RVSM空域上擴高度層中實施縮小垂直間隔標準提供參考，以期提高空域利用效率，降低高空尾渦遭遇風險。

1 飛機尾渦物理模型

1.1 尾渦初始強度計算模型

飛機尾渦一般使用渦旋環量Γ表示其強度。根據圓柱繞流氣動力知識，機翼微元上的升力計算公式為：

l(x)=ρ∞v∞Γ(x)

(1)

式中：ρ∞為大氣密度；v∞為飛機真空速；Γ(x)為翼剖面附著渦環量；x為翼剖面與飛機縱軸之間的距離。對整個翼展積分，飛機升力L的計算公式為：

(2)

式中：B為飛機翼展。對于后掠翼飛機，翼剖面環量的計算公式為：

(3)

(4)

所以，得尾渦初始強度計算公式如下：

(5)

式中：n為飛機法向過載；W為飛機質量。由上式可以看出，尾渦初始環量的大小與飛機質量、空氣密度、飛機速度、翼展等因素相關。

1.2 尾渦消散過程

綜合考慮尾渦消散的隨機特性，Holz?pfel和Robins應用激光雷達開展多次尾渦探測試驗[17]，在D2P模型基礎上添加隨機擾動項，形成尾渦隨機兩階段消散模型(probabilistic two-phase wake vortex decay，P2P)。尾渦的消散主要受大氣參數及飛機特性影響，P2P模型可以用來描述不同飛行高度處的尾渦消散情況。

為了計算方便，通常使用無量綱基準參數。常用的無量綱基準參數包括參考下沉速度w0和尾渦參考時間t0，具體計算公式如下：

(6)

(7)

式中：b0為尾渦初始渦核間距，通常為πB/4。

根據P2P模型，尾渦的消散可分為2個階段：擴散階段及快速衰減階段。在擴散階段，尾渦消散的速率較為緩慢，尾渦環量計算公式如下：

(8)

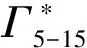
(9)

ε*=(εb0)1/3/w0

(10)

用浮力頻率N表征大氣層結穩定度，無因次浮力頻率N*的計算公式如下：

(11)

(12)

式中：hf為飛機的飛行高度；T為所在飛行高度的溫度；Cp為定壓比熱。與平流層相比，通常對流層內大氣層結穩定度較低。

1.3 尾渦下沉模型

尾渦形成后由于相互誘導作用而向下運動，渦核位置發生變化。渦核下沉速度vs及經時間t渦核下沉高度hs的計算公式如下：

(13)

(14)

在實際大氣中，尾渦的強度消散和渦核下沉運動會對下方飛機的飛行安全造成不利影響。通過計算并對比高空和中低空的尾渦運動差異，可以定量地評估在高空實施縮減尾流垂直間隔的可行性及安全性。

2 尾渦運動特性計算分析

2.1 計算模型的驗證分析

SESAR和EUROCONTROL針對歐洲空域內飛機巡航階段的尾渦遭遇安全問題聯合開展R-WAKE項目[18]。分別以形成尾渦流場的前機為A320、A330、B777，飛行高度為39 500 ft，在渦流耗散率ε及浮力頻率N均為0的條件下，參考文獻[18]給出R-WAKE項目的尾渦遭遇模擬數據。統計前機后方不同縱向位置處的尾渦渦核下沉高度，與第1節中模型的計算結果進行對比，如表1所示。相對誤差基本在4.2%范圍內，說明文中模型的計算精度可以接受。

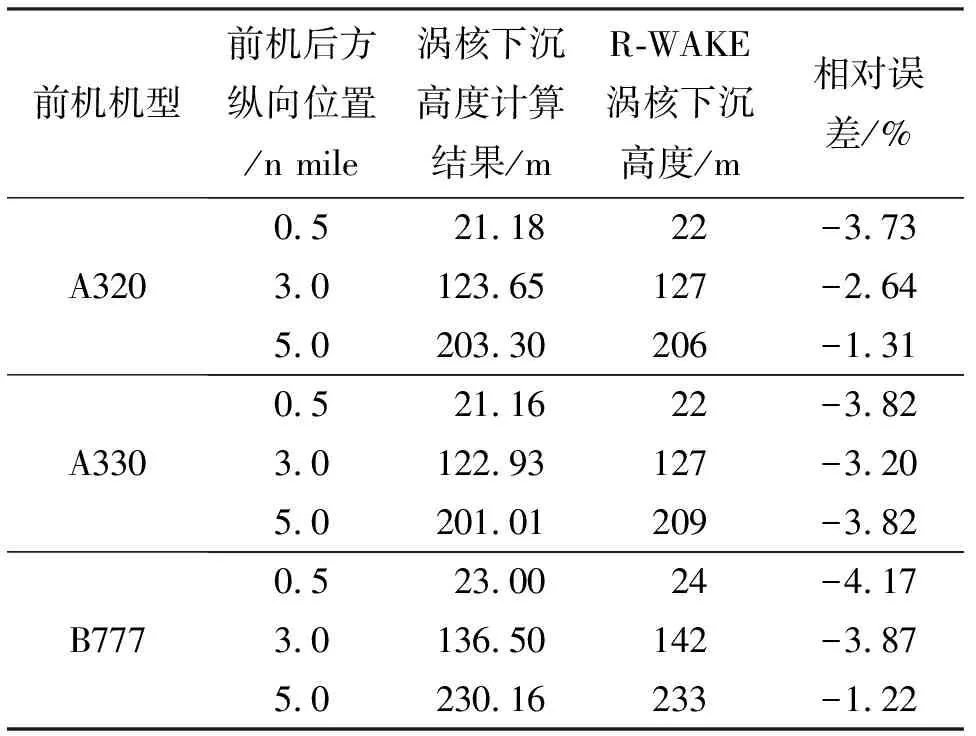
表1 尾渦渦核下沉高度數據對比

2.2 仿真實驗條件

考慮在飛機飛行過程中飛機的重量、速度及大氣參數的不確定性，采用蒙特卡洛方法(Monte-Carlo approach)對尾渦的運動情況進行仿真模擬。蒙特卡洛模擬屬于概率分析法，使用隨機變量代替常量，同時保證隨機變量符合一定的概率分布，使最終結果更加逼近使用常量時所得到的計算結果。蒙特卡洛仿真的具體實驗條件如表2所示。

表2 蒙特卡洛仿真實驗條件

2.3 尾渦渦核下沉計算分析

根據式(1)～(5)，使用蒙特卡洛方法對某重型機在不同飛行高度處的尾渦初始環量進行10 000次仿真計算，得到不同飛行高度處的尾渦初始環量均值如圖1所示。由圖1可以看出，高空中的尾渦初始環量較大，15 000 m飛行高度處的尾渦初始環量約為中低空尾渦初始環量最小值的3.1倍。因此在高空飛行范圍內，仍有尾渦遭遇不安全事件的發生和報道。

圖1 蒙特卡洛仿真模擬的尾渦初始環量Γ0均值

前機下方形成的尾渦危險區與后機所能承受的尾渦強度Γa有關，尾渦危險區在垂直范圍上表示為尾渦環量消散到Γa時的渦核下沉高度。為反映不同飛機所能承受的尾渦強度不同，令Γa分別為150 m2/s、100 m2/s、50 m2/s，計算尾渦渦核下沉高度。依據機型性能數據和仿真實驗條件，使用蒙特卡洛方法對某重型機在不同飛行高度處的尾渦渦核下沉高度進行10 000次仿真計算，得到尾渦下沉高度平均值和標準差，仿真結果如圖2和圖3所示。

從圖2可以看出，12 500 m以上的高空中，尾渦環量消散到Γa時渦核下沉高度隨飛行高度的增加而增加。這是因為飛行高度增加后，尾渦初始環量增大，因此由渦核的下沉高度計算公式可知，飛行高度增加，高空渦核的下沉速度相對較大，導致高空渦核下沉高度增加。從圖3可以看出，12 500 m以上的高空中，隨飛行高度增加，渦核下沉高度的標準差降低，因此外界因素的不確定性變化對高空渦核下沉運動的干擾較小。

圖2 蒙特卡洛仿真模擬的渦核下沉高度均值

圖3 蒙特卡洛仿真模擬的渦核下沉高度標準差

與中低空相比，12 500 m以上高空中的渦核下沉高度在增大。為了計算12 500 m以上高空尾渦渦核下沉高度增大的幅度，設尾渦環量消散到Γa時，高空尾渦渦核最大下沉高度為hmax，中低空尾渦渦核最小下沉高度為hmin，則尾渦渦核下沉高度差值Δh的計算公式如下：

Δh=hmax-hmin

(15)

2.4 高空與中低空的渦核下沉運動差異性分析

計算不同蒙特卡洛仿真實驗次數下的Δh，統計平均值與相對標準差，結果如圖4及圖5所示。可以看出，高空尾渦渦核下沉高度平均增加量為42.4～49.7 m，相對標準差為14.4%～17.6%。當實驗次數超過10 000次后，計算結果與仿真實驗次數基本無關聯。

圖4 不同實驗次數下的Δh平均值

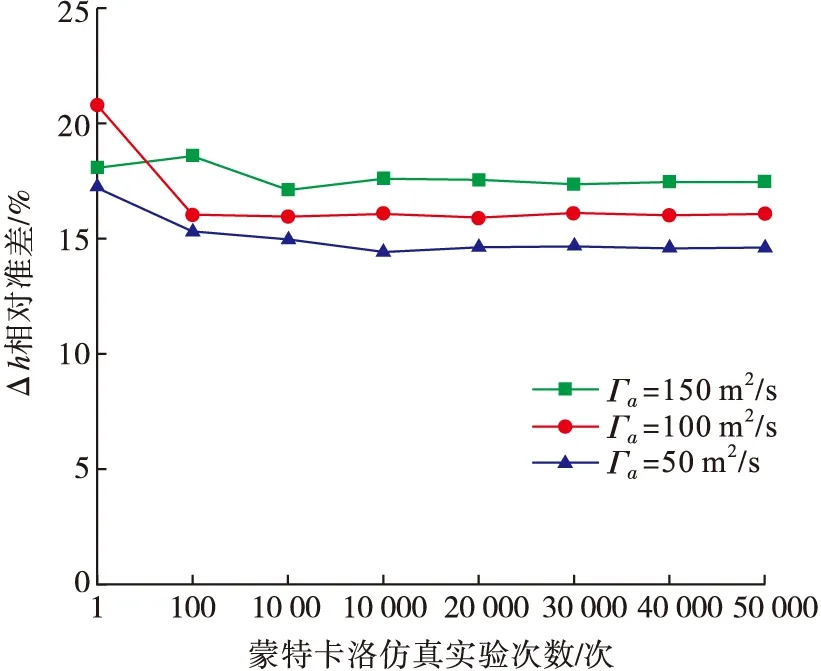
圖5 不同實驗次數下的Δh相對標準差

當環量消散到100 m2/s，統計50 000次蒙特卡洛仿真實驗下的Δh分布情況，繪制頻數分布直方圖及對應的概率密度函數曲線，如圖6所示。由圖6可以看出，Δh的仿真值大部分分布在35～55 m范圍內，呈正態分布規律。

圖6 Δh的分布概率密度函數

表3為Δh的具體區間分布情況。由表3可以看出，Δh最大值所在區間為80～85 m，最小值所在區間為15～20 m。渦核下沉高度差值在45～50 m區間內出現次數最多，占比約為28.3%。根據蒙特卡洛仿真模擬得到的計算數據，當飛機參數及外界因素發生不確定性變化時，高空與中低空尾渦渦核下沉高度存在較大差異。

表3 Δh的區間分布

3 影響因素分析

飛機特性及大氣條件均會對尾渦的消散及運動造成影響。此節分析飛機質量以及大氣湍流度的變化對RVSM空域上擴高度層中的尾渦渦核下沉高度的影響。

3.1 飛機質量對尾渦下沉高度的影響

飛機的形狀和質量影響形成尾渦的初始強度，進而影響尾渦的消散和渦核的運動，其中飛機質量是主要的影響因素[19]。為了分析飛機質量對尾渦下沉高度的影響，按照飛機質量350～390 t，其余初始條件同2.2節的條件，由尾渦物理模型計算15 000 m飛行高度處當尾渦環量消散到100 m2/s時對應的尾渦下沉高度。圖7為不同飛機質量下進行10 000次蒙特卡洛仿真實驗數據的統計值，包括中位數、60%～90%概率值等。

圖7 不同飛機質量下尾渦下沉高度變化趨勢

從圖7可以看出，高空尾渦渦核下沉高度隨飛機質量的增加而增加。這是因為飛機質量增加后，導致尾渦初始環量增加，渦核的下沉速度相對較大，因此由渦核下沉高度的計算公式可知，飛機質量增加，導致渦核下沉高度增加。飛機質量從350 t增加到390 t的過程中，渦核下沉高度最大增加4.4 m，變化范圍為1.7%～2.1%。

3.2 大氣湍流度對尾渦下沉高度的影響

高空中的大氣湍流度較低，為了分析大氣湍流水平對尾渦渦核下沉高度的影響，按照渦流耗散率10-5～10-3m2/s3，其余初始條件同2.2節的條件計算15 000 m飛行高度處當尾渦環量消散到100 m2/s時對應的尾渦下沉高度。圖8為不同大氣湍流度下進行10 000次蒙特卡洛仿真實驗數據的統計值，包括中位數、60%～90%概率值等。

圖8 不同大氣湍流度下尾渦下沉高度變化趨勢

從圖8可以看出，隨著渦流耗散率增大，高空尾渦渦核下沉高度減小。這是因為渦流耗散率增大，意味著大氣紊亂程度增加，使得尾渦消散進入快速衰減階段的時間提前[20]，從而加快尾渦消散過程，渦核下沉高度降低。

4 結語

1)隨著飛行高度的增加，12 500 m以上高空空域內的渦核下沉高度在增加。與中低空相比，使用蒙特卡洛模擬得到的渦核下沉高度增加量均值為42.4～49.7 m。

2)飛機質量通過改變尾渦初始強度進而影響尾渦渦核運動；大氣湍流度通過改變尾渦消散過程進而影響尾渦渦核運動。飛機質量的增加會導致高空尾渦渦核下沉高度增加，大氣湍流度的增加會導致尾渦渦核下沉高度減小。因此飛行參數及大氣湍流條件的改變可以降低尾渦影響范圍，提高尾渦遭遇安全性。

3)空域資源的日趨緊張使得進一步提升飛機升限、充分利用高空資源越來越迫切，在12 500 m以上空域內實施縮小垂直間隔時，應警惕前機尾渦所帶來的不利影響。下一步擬通過流場數值模擬方法或探測系統獲得大量的高空尾渦衰變及運動數據，進一步研究高空飛行中的尾渦流場演化特性。