穩健估計在地鐵沉降監測數據處理中的應用

陳志江，楊久東，張凌云

(華北理工大學 礦業工程學院，河北 唐山 063210)

隨著城市不斷發展，出行方式上越來越多樣化，地鐵交通也成為人們出行方式之一。在城市地鐵施工中，不可避免地受到溫度、壓力等影響，對基坑周圍產生沉降變形[1]，這些形變對生產施工帶來安全隱患，因此，獲取連續監測變形數據對合理判斷和預判地鐵沉降至關重要。為了滿足城市地鐵的建設，許多學者對于深基坑變形規律和安全穩定性開展了大量的研究。王興使用變形監測數據，運用傳統模型數值分析、神經網絡預測模型、灰色系統理論以及時間序列分析幾種方法的對比與分析，進行基坑變形的預測[2]。唐永澤等針對深圳某大廈基坑工程，研究復雜條件的環境下深基坑對周圍環境的影響，為工程施工和監測提供基礎[3]。張永超等運用非等時距灰色預測數學模型，對基坑監測數據進行分析和檢驗[4]。任麗芳等和徐志彪基于ELM神經網絡模型和土體損傷模型對基坑變形開展預測研究[5,6]。

在沉降監測過程中，采取任何高精度水準儀器或者測量方式，其觀測數據中可能會存在由于多種原因造成的粗差，例如觀測者操作不當、儀器出現故障、觀測條件不利等因素。在含有粗差的數據處理中，使用最小二乘方法不可避免將粗差帶入計算中從而導致整體計算的準確性[7]，對實際施工造成誤判。所以需要使用穩健估計的方法，把觀測數據中粗差剔除，對數據處理不產生影響。該研究采用最小二乘法和穩健估計法2種不同的數據處理方法，對比存在粗差和不存在粗差的數據進行分析，驗證穩健估計的抗差效果的優越性[8-10]。

1研究方法和理論

在地鐵的施工測量時，觀測時系統誤差與偶然誤差是不可避免的，除此之外，還常有忽略的粗差，如由于外部條件的干擾和外部條件的改變，測量人員的疏忽等原因造成的粗差，如果不剔除這些粗差，直接對其進行平差處理，一定會對數據處理與分析產生影響。為了降低、剔除粗差對數據處理的影響，在數據處理中選擇一些算法對粗差進行處理，獲得盡可能接近真實測量的有效估計。

1.1 回歸分析

在建立線性回歸分析模型時，首先將數據中因變量y和自變量x1,x2,…,xn分為兩組，因變量y和自變量xn之間存在一定的函數關系[11]，如果因變量y和自變量xn之間為線性關系，即：

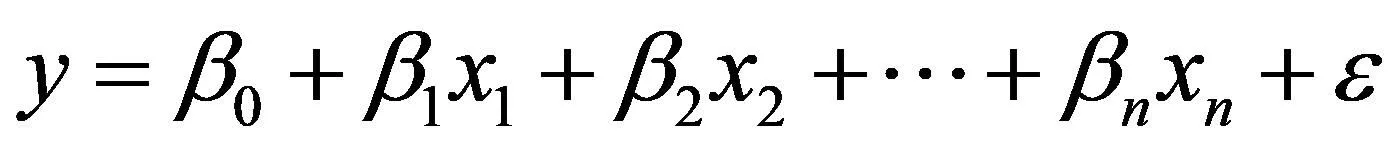
(1)

在式(1)中，β1、β2、…、βn為回歸系數，β0為回歸方程常數項，ε為隨機擾動項，其數學期望為0。

1.2 最小二乘原理

最小二乘估計法：通過最小化誤差的平方求和，尋找數據的最佳函數擬合。利用最小二乘估計法可以快速地求出未知的數據，并使得這些求得的數據與實際數據之間誤差的平方和為最小[12]。

函數模型：

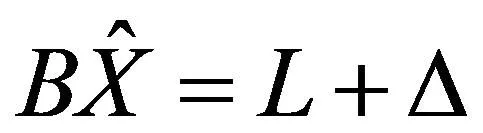
(2)

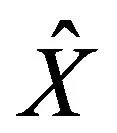
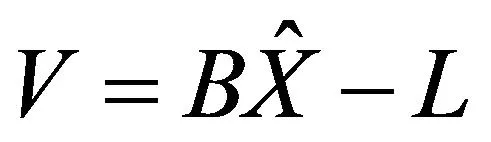
(3)

最小二乘平差準則就是：

(4)

根據上式可得最小二乘解：

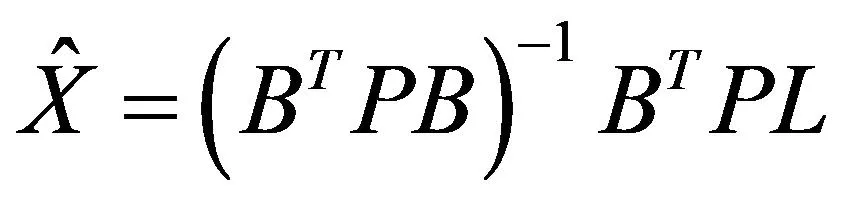
(5)

1.3 穩健估計原理

在粗差無法避免的情況下，選擇合理的估計模型，使參數估值盡量避免由觀測數據粗差所帶來的偏離真值，得到一般情況下最優參數估計，參數估計的原則是充分利用觀測數據中有效的數據信息，排除或者降權無效或有害信息，由于事先不知道具體觀測數據中有效信息和無效信息的分布情況，所以在數據處理上，采用抗差的方法，為了獲取一些可靠的、具有實際意義的有效估值，舍棄一部分觀測粗差[13,14]。

穩健估計平差準則：

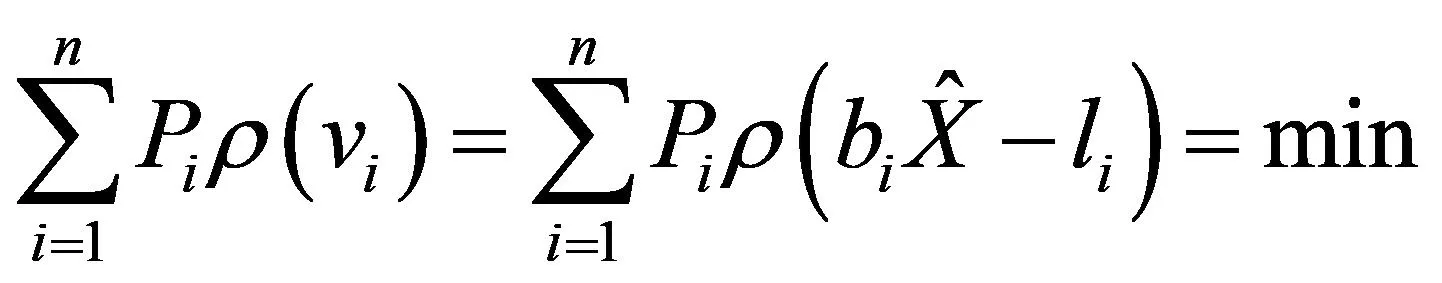
(6)

穩健估計解：

(7)

本文采取的是Andrews法：

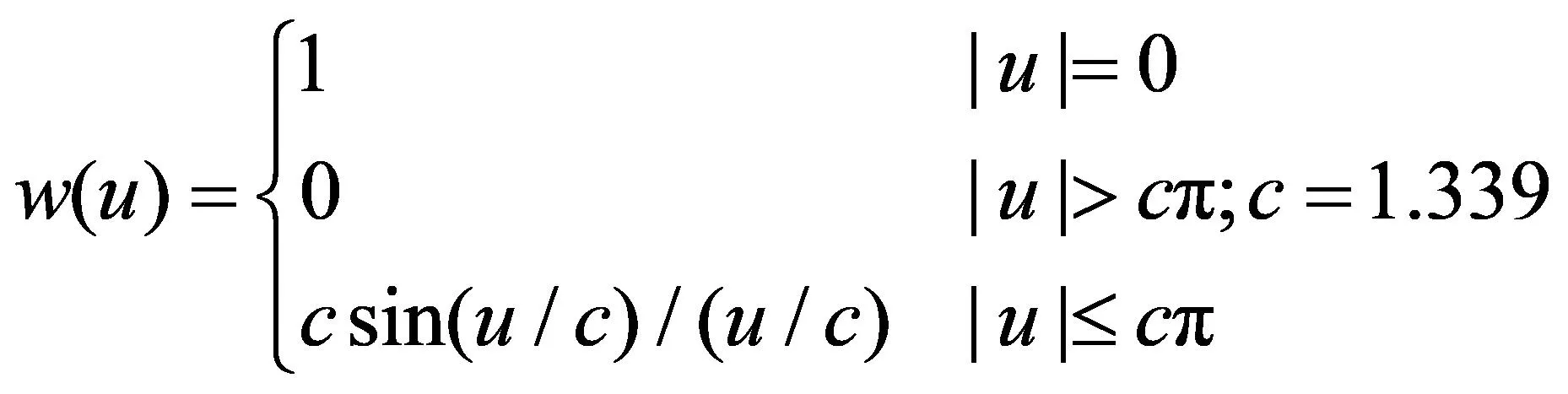
(8)

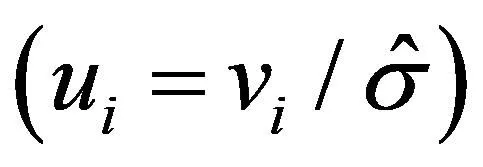
3案例分析

3.1 數據采集

為了驗證穩健估計數據處理的可行性，現以深圳市某地鐵的基坑沉降點高程監測數據為參考，鑒于文章篇幅限制，只截取2019年9月1日至12月1日DB-11-01監測點號觀測數據，以周為單位，總共14個周報數據，地鐵沉降點DB-11-01監測數據如表1所示。利用截取14個周報觀測數據進行最小二乘和穩健估計模型擬合，通過擬合模型分析數據異常的具體原因。

表1 DB-11-01沉降點監測數據

3.2 實驗對比分析

3.2.1不含粗差的數據分析

利用MATLAB軟件，分別使用最小二乘法和穩健估計，將外業采集到的水準沉降數據進行回歸分析。

通過圖1原始數據殘差圖可以看出，14個觀測數據誤差都在允許的范圍內，不存在明顯粗差。

圖1 原始數據殘差圖

利用最小二乘法得到的一元方程系數b0=-1.317 7，b1=-0.190 4，故最小二乘法得到的一元線性回歸方程為：

(9)

同理利用穩健估計回歸分析得到一元線性回歸方程系數b2=-1.317 6，b3=-0.190 4，故穩健估計法得到的一元線性回歸方程為：

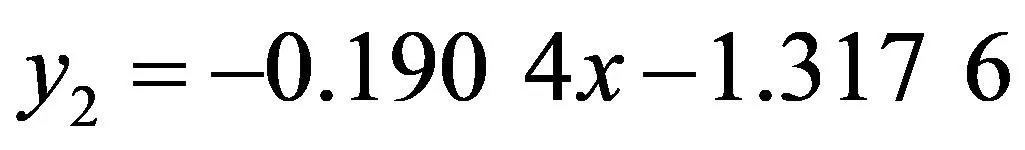
(10)

圖2所示為無粗差下2種不同方法擬合方程圖：

圖2 無粗差2種不同方法擬合方程圖

通過計算可以得出，在觀測數據不存在粗差的情況下，2種方法方程幾乎一樣，其中1.460 0、1.519 6分別表示使用最小二乘法、穩健估計分析的中誤差，采用最小二乘法和穩健估計法計算殘差平方和均為27.709 2，說明在不存在粗差的情況下，最小二乘和穩健估計擬合效果相差不大。

3.2.2含粗差的數據分析

將外業2019年12月1采集到的數據認為加入粗差，原始觀測-20.33修改為-24.33，處理后的殘差圖如圖3所示：

圖3 加入粗差數據殘差圖

通過圖3加入粗差數據殘差圖可以看出，12月1日觀測數據是一個明顯的粗差。

最小二乘分析的到回歸系數b4=-1.329 9，b5=-0.192 5，故最小二乘法得到的一元線性回歸方程為：

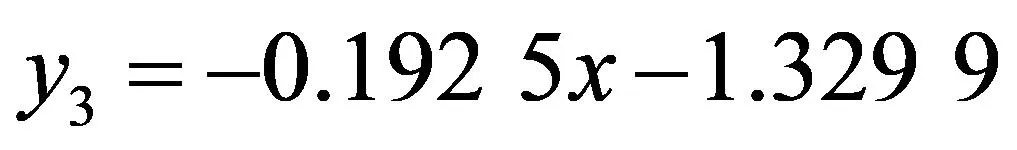
(11)

同理利用穩健估計回歸分析得到一元線性回歸方程系數b6=-0.860 6，b7=-0.206 7，故穩健估計法得到的一元線性回歸方程為：

(12)

圖4所示為加入粗差后2種不同方法擬合方程圖：

圖4 加入粗差后2種不同方法擬合方程圖

從圖4中可以看出，在60～90 d累計觀測時間段穩健估計擬合效果更好，更加接近存在粗差時真實的觀測值。通過計算可以得出，在原數據加入粗差的情況下，兩者方程差異顯著，其中采用最小二乘法和穩健估計法計算的中誤差分別為2.020 5、1.898 6，通過中誤差數據，可以明顯得到，利用穩健估計法得到的中誤差要小于利用最小二乘法得到的中誤差，利用最小二乘法與穩健估計法計算殘差平方和分別為55.760 4、53.073 8，從殘差平方和結果可以看出，利用穩健估計法得到的殘差平方和要小于最小二乘法得到的殘差平方和。通過最小二乘法和穩健估計估計法中誤差和殘差平方和對比可知，在觀測數據中存在粗差的情況下，穩健估計相較于最小二乘擬合效果更好。

4結論

(1)在沉降觀測數據沒有粗差時，采用最小二乘法和穩健估計法分別對觀測數據處理時，2種方法中誤差和殘差平方和沒有明顯差異，都可用于沉降觀測。

(2)當沉降觀測數據存在粗差時，采用最小二乘法在數據處理時，計算結果偏差較大，擬合效果偏離真實值，采用穩健估計法時，其擬合效果以及中誤差和殘差平方和，均優于最小二乘法估計，能夠對存在粗差的觀測數據起到抗差的作用。