光晶格中自旋軌道耦合玻色-愛因斯坦凝聚體的非線性能譜特性*

張愛霞 姜艷芳 薛具奎

(西北師范大學物理與電子工程學院, 蘭州 730070)

(2021 年4 月14 日收到; 2021 年5 月26 日收到修改稿)

1 引 言

光晶格中的超冷原子物理在理論上和實驗上受到了人們的重點關注. 因為光晶格不存在任何雜質和缺陷, 且光晶格中的超冷原子系統可以在廣泛的參數范圍內調節, 為量子計算和強關聯多體系統的量子模擬創造了理想的條件, 例如量子糾纏以及拓撲相變的研究等[1-4]. 此外在光晶格系統中還發現了許多有趣的動力學現象, 例如Bloch 振蕩[5-10]、Landau-Zener 隧穿[11-14]、局域化[15,16]、超流相到莫特絕緣相的相變[17,18]等. 更重要的是, 原子間相互作用的非線性還可以極大地改變布洛赫帶的結構, 使能帶在第一布里淵區的邊界處呈現出燕尾形狀的環狀結構(loop 結構)[19-23]. 這主要是由光晶格勢和非線性相互作用之間的競爭導致的, 當相互作用較大時, 能帶中會出現loop 結構. 可以通過觀察Bloch 振蕩的破壞以及非線性Landau-Zener隧穿現象的發生, 間接地證明能帶中loop 結構的存在[9]. 因此光晶格周期勢為研究玻色-愛因斯坦凝聚體的相關物理特性提供了很好的平臺[24-32].

近年來, 利用光與原子間的相互作用, NIST小組在87Rb 玻色-愛因斯坦凝聚體中實現了一維人工自旋軌道耦合, 為超冷原子氣體的研究開辟了新的思路[33]. 隨后, 山西大學和中國科學技術大學分別在40K 費米氣體和87Rb 冷原子中實現了二維自旋軌道耦合[34,35]. 最近, 中國科學技術大學與北京大學等合作, 通過將普通光晶格和拉曼光晶格相對轉角的方法, 在國際上首次實現了三維人工自旋軌道耦合[36], 且構造出有且只有一對外爾點的理想外爾半金屬拓撲能帶結構, 超越了傳統凝聚態物理的外爾型拓撲物理的量子模擬, 為研究拓撲輸運性質以及量子模擬新奇現象打開了新的方向. 此外, 實驗上也成功實現了運動光晶格中自旋軌道耦合玻色-愛因斯坦凝聚體, 證明了自旋軌道耦合會破壞該系統的伽利略對稱性[37]. 光晶格中自旋軌道耦合玻色-愛因斯坦凝聚體的實現激發了人們對其基態特性的研究[38-40], 發現系統中存在4 種基態相, 即具有單一波矢的非極化和極化Bloch 相以及由兩個具有相反波矢Bloch 波疊加的條紋相. 同時初步研究發現, 對于靜止的光晶格, 一定參數范圍內的最低Bloch 帶還可以產生平帶, 且系統能量最小值可以出現在第一布里淵區內的任何位置[41].而移動的光晶格則會使Bloch 譜變得復雜, 這主要是由自旋軌道耦合系統中缺乏伽利略不變性導致的, 因此自旋軌道耦合成為導致系統能譜特性復雜化的又一重要因素. 事實上在自由空間, 自旋軌道耦合和原子間相互作用的耦合也會導致系統能帶中出現loop 結構, 并且伴隨著Landau-Zener 隧穿和自旋交換動力學[42]. 可以設想, 自旋軌道耦合與光晶格的耦合必然會使系統的能譜特性更加復雜化. 但是目前對光晶格中自旋軌道耦合玻色-愛因斯坦凝聚體的非線性能譜特性的研究還很初步.

本文主要研究了光晶格中自旋軌道耦合玻色-愛因斯坦凝聚體的非線性能譜結構和流密度. 先簡單地介紹了系統模型, 然后通過兩模近似和變分法得到了系統的能量, 接著展示了不同系統參數對布里淵區邊界附近能帶結構的影響, 討論了系統能帶在布里淵區邊界出現loop 結構的臨界情況, 最后研究了不同自旋態流密度的變化規律.

2 模型和變分法

2.1 理論模型

考慮一維淺光晶格中贗自旋1/2 的自旋軌道耦合玻色-愛因斯坦凝聚體, 自旋軌道耦合是由Rashba 和Dresselhaus 型自旋軌道耦合等權疊加形成的. 在平均場近似下, 該系統可以通過如下無量綱平均場能量泛函描述[37-40]:

研究發現, 光晶格對第一布里淵區附近自旋軌道耦合玻色-愛因斯坦凝聚體的基態能帶結構有顯著的影響[38-40]. 而且對于淺晶格或者中間深度的光晶格, 兩模近似不僅可以給出G-P 方程在最低能帶第一布里淵區邊界處的精確解, 還可以給出在布里淵區附近的近似解[5,6,11,19], 因此為了深入地研究布里淵區邊界附近最低能帶的變化特性, 使用如下形式的兩模近似試探波函數:

式中, 假定自旋對稱相互作用, 即g11=g22=g和δ=0. 為了獲得系統的能帶結構, 使用變分法, 對(5)式中的變分參數s和θ變分. 即令?E/?s=0 ,?E/?θ=0, 可得變分方程如下:

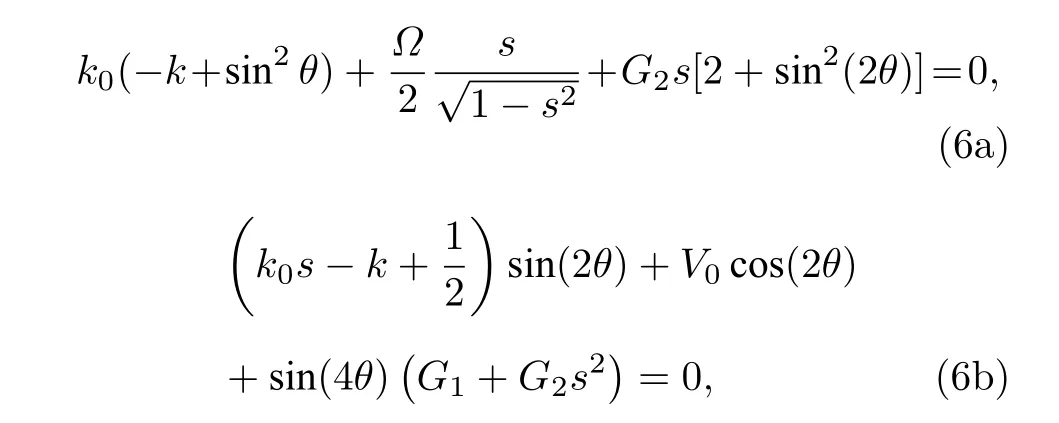
其中G1=(g+g12)/4 ,G2=(g ?g12)/4 . 通過數值求解變分方程中的θ和s, 并代入系統能量(5)式中, 便可以研究不 同參數下的能譜結構圖. 可以清楚地看到, 系統的能量是由拉曼耦合強度Ω, 自旋軌道耦合強度k0, 光晶格強度V0和原子間相互作用共同決定. 下面展示不同系統參數對能譜結構的影響.

2.2 非線性能譜結構

圖1 是在不同系統參數下的最低能帶. 可以看出, 在最低能帶的布里淵區的邊界處, 即k=0.5 處出現了特殊的loop 結構. 而且在每一行中(請看第2 行—第4 行中V0=0.2 情況), 隨著拉曼耦合Ω的增大, loop 寬度先變小, 然后在布里淵區邊界處出現尖點, 最后loop 消失. 每一列中, 隨著自旋軌道耦合強度k0的增大, 能帶先在邊界附近出現尖點, 繼續增大k0, 布里淵區的邊界處出現了loop 結構, 最后loop 的寬度變大的同時能帶結構變得更加復雜(如每一列中V0=0.2 情況). 在每一副子圖中不同顏色對應著不同的光晶格強度, 對于較小的光晶格強度V0, 能帶結構在布里淵區的邊界處先出現了較大的loop 結構, 繼續增大V0, 能帶在邊界處出現尖點, 最后loop 消失(如k0=0.3,Ω=1.5 情況). 總之, 我們發現拉曼耦合和光晶格強度抑制了最低能帶在邊界處loop 結構的出現, 自旋軌道耦合促進了loop 結構的產生, 使loop 結構變得更加復雜. 能帶結構中不同能量最小值處(圖1 中用小球表示)的凝聚體處于不同的基態相, 為了進一步研究能量最小值處凝聚體所處的基態相, 圖2 給出了不同拉曼耦合下的極化圖. 可以看出, 當自旋軌道耦合強度k0較小時(k0=0.2 ), 能量最小值處的凝聚體處于非極化的Bloch 相 (圖2 中的所有黑球).隨著k0的增大, 當s ?=0 時凝聚體處于極化Bloch 相,相反, 當s=0 時凝聚體處于非極化Bloch 相.

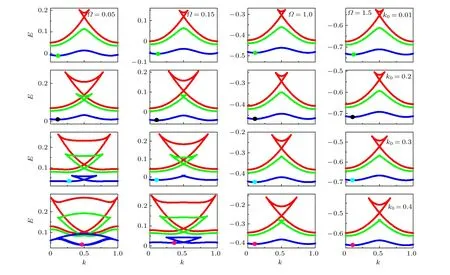
圖1 不同系統參數下的非線性能譜結構. 每副子圖中不同的顏色代表不同的光晶格強度, V0 =0.05 (紅色), 0.2 (綠色),0.4(藍色). 能量最小值處用不同顏色的小球表示. 其他參數:g =0.2, g12 =0.1Fig. 1. Nonlinear energy band structure for different system parameter. Different colored curves in every subplots correspond to different optical lattice strength, V0 =0.05 (red), 0.2 (green), 0.4 (blue). The energy minima is indicated by different colored ball. The other parameters are g =0.2 and g12 =0.1 .

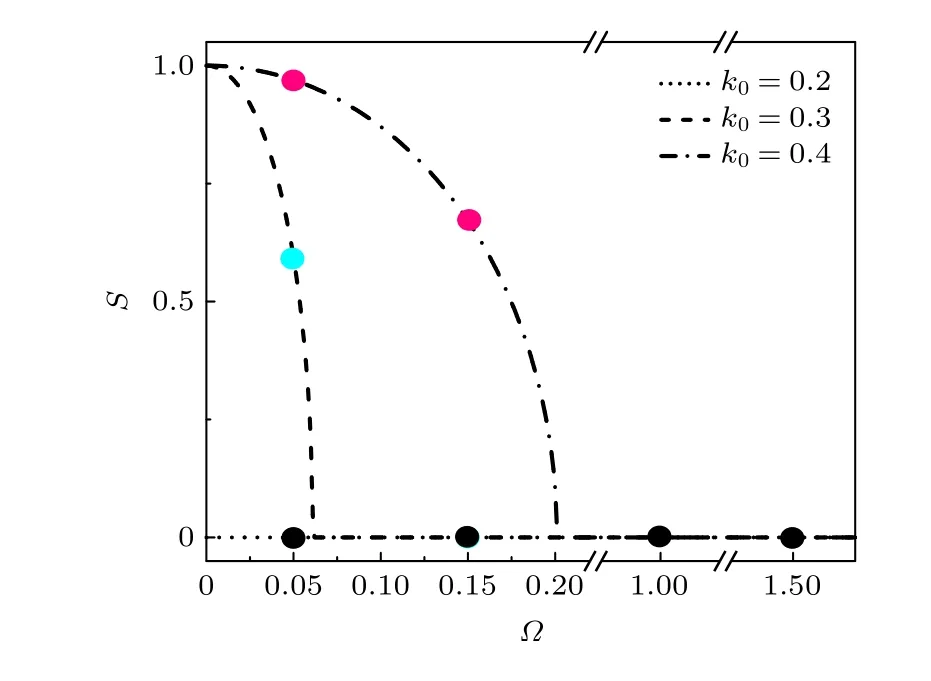
圖2 不同拉曼耦合 ? 下的極化圖. 其他參數:g =0.2,g12 =0.1,V0 =0.4Fig. 2. Spin polarization s as a function of Raman coupling ? for different k0 . The other parameters are g =0.2 ,g12 =0.1and V0 =0.4 .

能帶布里淵區邊界處loop 結構的出現, 還與原子間相互作用有關. 為了進一步研究原子間相互作用對能帶結構的影響, 圖3 中繪制了不同種間原子間相互作用g12下的能帶. 可以發現: 最低能帶中不僅在布里淵區的邊界處(k=0.5 )出現loop 結構, 在遠離邊界的兩端也有loop 的存在(圖中在k=0,1附近). 同時在高能帶的布里淵區邊界處也出現了loop 結構, 而且隨著g12的增大, 不同位置的loop 結構寬度都變大, 能帶中還會出現高低能帶loop 交叉等更加復雜的現象. 由此可知, 原子間相互作用的非線性效應會使能帶中loop 結構更加復雜.

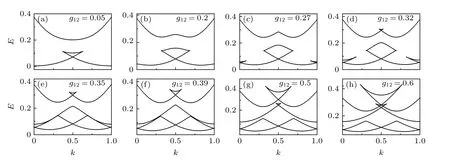
圖3 不同種間原子間相互作用 g12 下的非線性能譜結構. 其他參數: ? =0.1 , k0 =0.2 , V0 =0.1 ,g =0.1Fig. 3. Nonlinear energy band structure for different interspecies interaction g12 . The other parameters are ? =1.0 , k0 =0.4 ,g =0.2and g12 =0.1 .

2.3 能帶出現loop 結構的臨界條件

當最低能帶在布里淵區邊界處出現尖點時, 便是達到了出現loop 的臨界條件. 為了直觀地觀測不同參數對最低能帶布里淵區邊界處出現loop 結構的影響, 繪制了不同自旋軌道耦合k0下, loop 結構出現的臨界Ω圖(圖4). 從圖4 可以發現, 在k0-Ω平面, 較強的光晶格使loop 的區域向大自旋軌道耦合區域擴展. 當k0一定時, 弱拉曼耦合Ω有利于loop 結構的出現, 隨著k0的增大, 較強的拉曼耦合Ω才會使能帶中不出現loop. 此外, 增大種間原子間相互作用g12(圖4(b)和圖4(c)), 當k0較小時, 光晶格強度V0對能帶在布里淵區邊界處出現loop 結構的臨界Ω的影響減弱. 隨著k0的增大,較強的光晶格強度則需要更大的拉曼耦合值才能使最低能帶的邊界處不出現loop 結構.

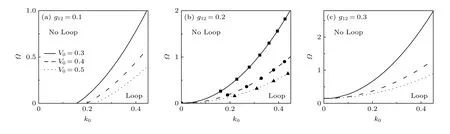
圖4 g =0.2 時最低能帶出現loop 的臨界 ? , (b) 中不同形狀的符號表示相應光晶格強度下(9)式給出的理論值Fig. 4. Critical condition for appearing the loop structure in the lowest energy band at g =0.2 . The different symbols in panel (b)represent the theoretical values given by Eq. (9) under the corresponding optical lattice strength.

為了進一步理解自旋軌道耦合、拉曼耦合、光晶格和原子間相互作用對形成loop 的競爭機理,針對g=g12的情況進行了理論分析. loop 結構最先在布里淵區邊界出現, 在變分方程(6a)和(6b)中令k=1/2且G2=0 , 即g=g12, 消去s可得

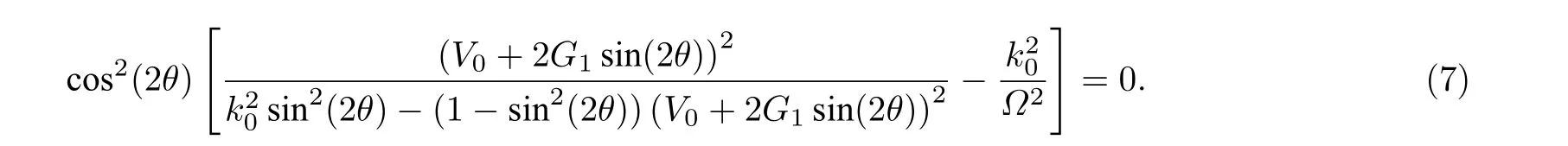
要想在布里淵區邊界出現loop 結構, 則方程(7)中的θ應有兩個解, 即滿足 cos(2θ)=0 和

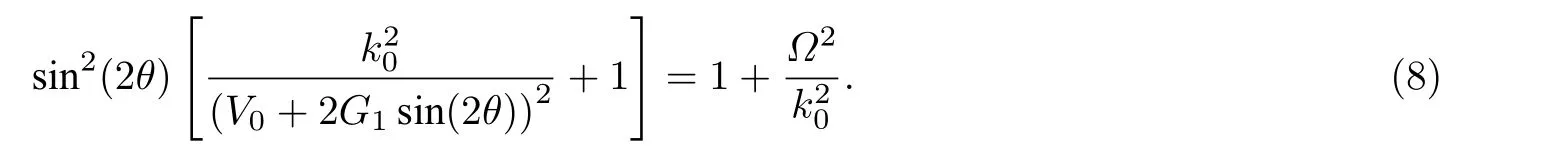
當sin(2θ)有根且滿足?1 ≤sin(2θ)≤1 時, 則有1+(Ω/k0)2≤/(V0?2G1)2+1,即

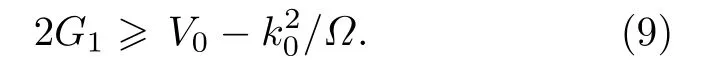
(9)式給出了g=g12時系統在布里淵區邊界處出現loop 結構的臨界條件. 圖4(b)中進一步展示了理論和數值結果的對比, 可以看出, 數值與理論符合得很好. (9)式充分揭示了自旋軌道耦合、拉曼耦合、光晶格和原子間相互作用對形成loop 的競爭機理, 即自旋軌道耦合k0的增大(拉曼耦合Ω的減小)等效于改變了系統的光晶格勢能, 亦即降低了在布里淵區邊界處出現loop 所需的非線性原子間相互作用能閾值. 當不存在自旋軌道耦合, 即k0=0時, (9)式退化為普通光晶格系統中出現loop 的臨界條件, 即相互作用能大于光晶格勢能.總之, 自旋軌道耦合和原子間相互作用促進了系統最低能帶loop 結構的出現, 拉曼耦合和光晶格抑制了loop 結構的產生.

3 凝聚體流密度

在布里淵區的邊界附近, 非線性能譜結構的變化與凝聚體的流密度密切相關, 不同自旋態的流密度定義如下:

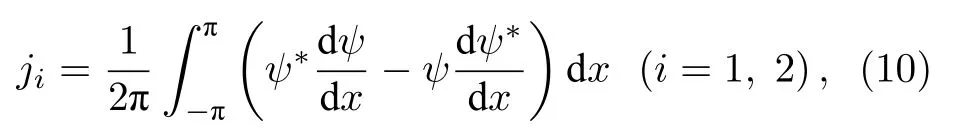
將兩模近似波函數(4)代入(10)式可得不同自旋態的流密度

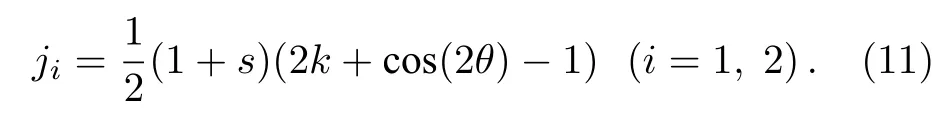
數值求解變分方程組(6a)和(6b)中的s和θ,代入(11)式可得到在布里淵區邊界附近非線性Bloch 波的流密度. 圖5 是與能帶圖圖1 第二列對應的不同自旋態的流密度圖. 從圖5 可以發現, 當自旋軌道耦合強度k0較小時, 不同自旋態的流密度基本重合. 若能帶在布里淵區邊界處無loop 結構,則在k=0.5 處的凝聚體流密度為零, 即ji=0 , 凝聚體將維持Bloch 振蕩, 同時將伴隨著弱的自旋交換(例如k0=0.01,V0=0.2 ). 隨著k0的增大, 雖然布里淵區邊界處的凝聚體流密度ji仍然為0, 但是流密度呈現出一定的不對稱性(例如k0=0.1,V0=0.2), 且在動量空間中不同自旋態流密度的分布發生分離, 凝聚體在進行Bloch 振蕩的同時, 自旋交換加強. 繼續增大k0, 在布里淵區邊界附近相同凝聚體動量所對應的流密度ji出現多值, 相應的能量值出現多根, 所以能帶結構在布里淵區邊界處出現了loop 結構(例如k0=0.2,V0=0.2 ), 破壞了系統的Bloch 振蕩, 使原子在不同Bloch 帶之間發生了非線性Landau-Zener 隧穿, 由于兩自旋態的流密度在動量空間的分布明顯分離, 因此自旋交換也加強. 另外, 從圖5 還發現, 光晶格強度的增大不僅減小了能帶結構布里淵區邊界處的loop寬度,同時使不同自旋態的流密度在動量空間中重合, 減弱了流密度的不對稱性和自旋交換.

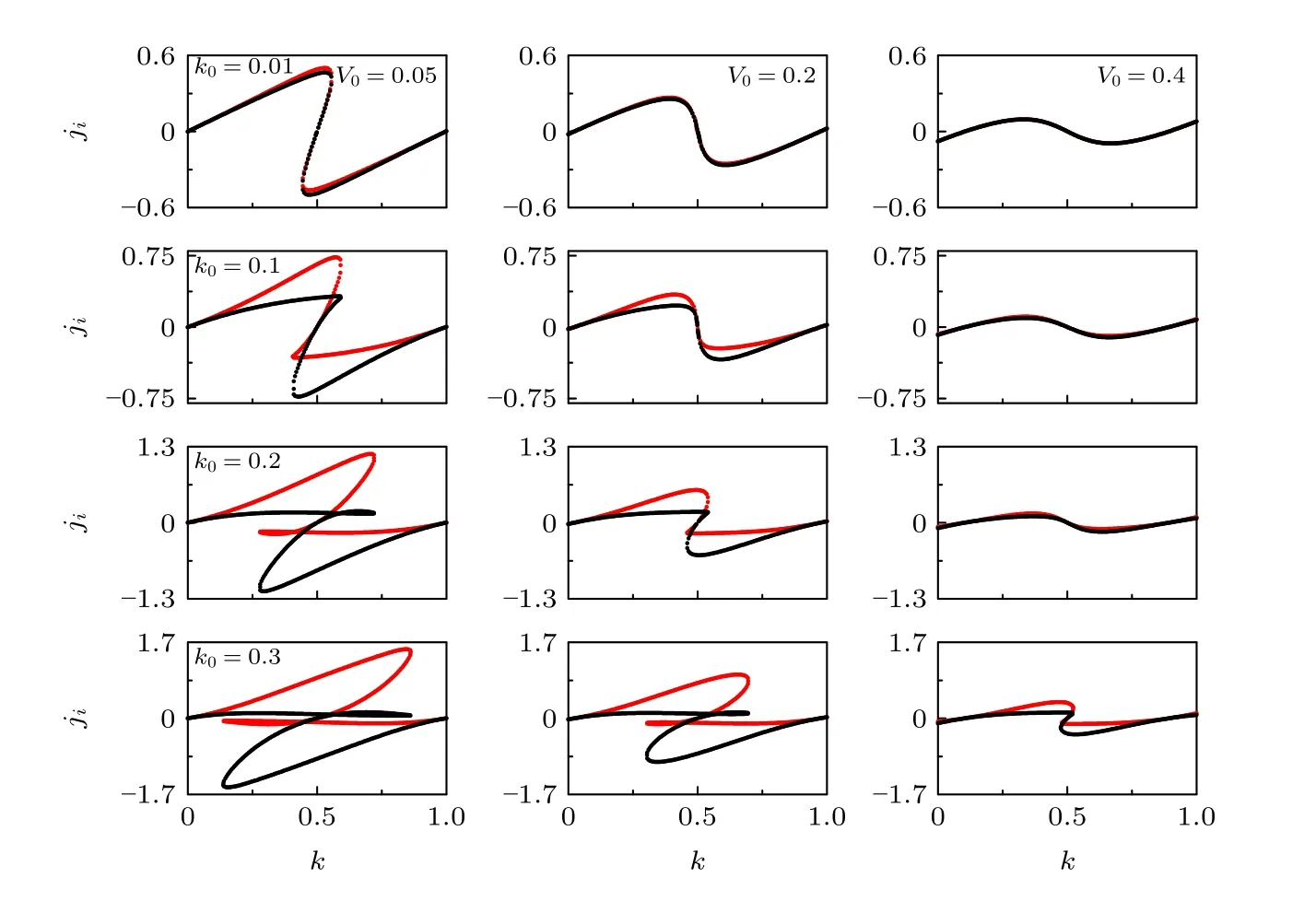
圖5 不同自旋軌道耦合 k0 和光晶格強度 V0 下的凝聚體流密度. 其他參數: ? =0.15 , g =0.2 , g12 =0.1 . 圖中紅色和黑色的線表示不同自旋態的凝聚體流密度Fig. 5. Current density for different spin-orbit coupling k0 and optical lattice strength V0 . The other parameters are ? =0.15 ,g =0.2and g12 =0.1 . The red and black lines represent the current density of different spin states.

圖6 進一步研究了自旋軌道耦合與拉曼耦合對不同自旋態流密度的耦合影響. 從圖6 可以直觀地發現, 隨著Ω的增大, 能帶結構中loop 寬度減小的同時, 凝聚體流密度的不對稱性減弱. 當自旋軌道耦合強度k0較小時(圖6 第一、二行k0=0.1 ),不同自旋態的流密度基本重合且自旋交換較小, 但是隨著k0的增大(圖8 第三、四行k0=0.2 ), 不同自旋態的流密度呈現出明顯的不對稱性. 而Ω的增大會強烈地減弱這種不對稱性, 使不同自旋態的流密度的變化規律與無自旋軌道耦合的情況相似. 同時還發現, 在動量空間loop 寬度所對應的凝聚體動量, 正好與凝聚體流密度中出現多值所對應的動量區間一致(圖中用粉色垂線表示), 所以可以通過直接地觀測凝聚體流密度出現多值的區域來研究loop 結構的大小.

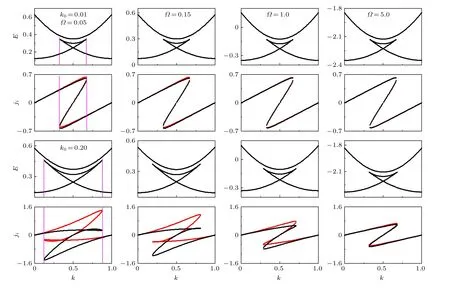
圖6 不同拉曼耦合 ? 下的能帶和相應的凝聚體流密度. 其他參數: V0 =0.05 , g =0.2 , g12 =0.1 . 圖中紅色和黑色的線表示不同自旋態的流密度Fig. 6. Energy band and current density for different Raman coupling ? . The other parameters are V0 =0.05 , g =0.2 and g12 =0.1. The red and black lines represent the current density of different spin states.

4 結 論

本文研究了光晶格中自旋軌道耦合玻色-愛因斯坦凝聚體的非線性能譜結構和流密度, 揭示了自旋軌道耦合、拉曼耦合、光晶格以及原子間相互作用對系統能帶特性的影響, 發現系統能譜結構在布里淵區的邊界處會出現loop 結構. 拉曼耦合和光晶格強度會抑制loop 結構的出現, 而自旋軌道耦合和原子間相互作用促進loop 結構的產生. 自旋軌道耦合會使能帶結構變得更加復雜, 而原子間相互作用的非線性還會使高能帶的布里淵區邊界處出現loop 結構. 非線性能譜結構的變化與凝聚體的流密度有密切的關系, 當能譜結構在布里淵區邊界處不存在loop 結構時, 邊界處的不同自旋態流密度為零. 出現loop 結構時, 邊界處的凝聚體流密度出現多值. 此外, 自旋軌道耦合還會使布里淵區邊界附近的流密度呈現出強烈的不對稱性, 使不同自旋態流密度在動量空間的分布分離, 而光晶格強度和拉曼耦合強度則會減弱這種不對稱性, 使不同自旋態流密度重合. 布里淵區邊界處loop 結構的出現破壞了系統的Bloch 振蕩, 使系統發生Landau-Zener 隧穿, 而不同自旋態流密度在動量空間分布的分離意味著自旋交換動力學的出現.