基坑支護體系中圍護樁嵌固深度設計方法研究
江 朋,宛超群
(安徽省交通規劃設計研究總院股份有限公司,安徽 合肥 230088)
0 引 言
由于地下結構的蓬勃發展,基坑支護設計越來越得到大家的重視[1]。基坑設計中,圍護結構的樁長設計非常重要,因為其關乎到基坑工程的穩定程度;當前多數基坑設計均采用傳統的安全系數法來確定樁長[2]。傳統設計方法過于依賴土層參數的準確性,而勘察工作者在確定土層參數時往往存在樣本嚴重不足,不足以代表基坑工程的實際土層。因此,基坑工程事故屢見不鮮[3-4],究其原因,還是當前采用的安全系數法不能夠考慮到土層參數的不確定性,在地層差異較大的區域安全程度遠遠不夠。
由于安全系數法在工程實際應用中存在一定的問題,故有很多研究者嘗試采用極限狀態設計的方法代替安全系數法。陳昌富等[5]利用條分法的公式,建立了基坑穩定性的極限狀態方程,利用極限狀態設計方法進行了基坑的穩定性分析。彭海銘等[6]利用極限狀態設計方法對基坑坑底隆起進行了分析,結果顯示此方法具有一定的指導價值。盡管學者們對基坑支護體系的可靠度分析方法有了一定研究,但是還很少有真正的去指導基坑設計。
本文建立了基坑抗隆起穩定性的極限狀態方程,計算得到了各土層參數的不確定性對隆起穩定性的影響,以此來確定圍護結構樁長的設計值。
1 基坑樁錨支護結構嵌固深度可靠度分析模型
1.1 地基承載力模式的抗隆起穩定性確定性計算模型
地基承載力模式的抗隆起分析方法是以驗算圍護樁體底面的地基承載力作為抗隆起分析依據。圖1為基坑工程橫斷面圖,h為基坑深度,ld為圍護結構的插入深度。地基極限承載力Pu計算公式為[8]:
Pu=γ2ldNq+cNc
(1)
式中:rm2為基坑內圍護樁底面以上土體重度;c為基坑內圍護樁底面以上土體的黏聚力;Nc、Nq為承載系數,當基底按粗糙情況處理時,由Prandtl(1920)計算公式分別為:

(2)
Nc=(Nq-1)/tanφ
(3)
式中:φ為基坑內圍護樁底面以上土體的內摩擦角。
此外,在地面均布荷載及自重荷載作用下,基坑外圍護樁底面處受到的荷載P為:
P=γ1(h+ld)+q0
(4)
式中:rm1為基坑外圍護樁底面以上的土體重度;q0為地面均布荷載。
因此,基坑坑底抗隆起安全系數K為:

(5)

圖1 地基承載力模式抗隆起分析
1.2 基坑抗隆起穩定性可靠度計算模型
根據前面公式,基坑工程坑底穩定性程度由土層參數決定。由于勘察工作者在確定巖土參數時試驗樣本不足,試驗方法不夠完善,提供的土層參數會存在一定的誤差。特別是對于土層差異性較大的地區,土層參數會存在一定的不確定性[9]。因此,結合極限狀態設計理論及前式,建立了基坑抗隆起穩定性極限狀態方程:
g(Z)=g(c,φ,γ1,γ2,q0)=Pu-P
=γ2ldNq+cNc-γ1(h+ld)-q0
(6)
極限狀態設計方法的原理是將式(6)中的所有參數當做服從特定概率分布的隨機變量來考慮,利用概率統計的方法,計算得到可靠度指標β,用以作為基坑抗隆起穩定性的控制指標。可靠度指標計算方法較多,其中驗算點法是計算可靠度指標最常用的方法。
根據可靠度指標的定義[9],β的計算表達式為:

(10)
其中:Xi分別對應c、φ、r1、r2、q0這5個參數,且認定這5個變量為隨機變量,服從正態分布型式。其余變量變異性較小,假定其為常量。
分別對這5個隨機變量進行求導,得到以下結果:

(11)

(12)

(13)

(14)

(15)
2 工程實例設計分析
2.1 參數取值
取某一典型支擋式基坑進行設計分析,該基坑安全等級為一級;基坑外共有兩層土層,第一層5 m,第二層20 m;而基坑內位于第二層土層。主要參數表表1所示。

表1 基坑支護結構主要參數
2.2 圍護樁嵌固深度的常規設計
根據基坑坑底抗隆起穩定性計算公式計算穩定性系數,不同樁長插入深度對應的抗隆起穩定性安全系數見圖1及表2。由計算結果可知,地基極限承載力Pu、圍護樁底面荷載P均隨著樁長插入深度的加大而顯著的增大,但地基極限承載力Pu的增加幅度更大,因此坑底抗隆起安全系數也會增大。根據規范[8],安全等級為一級的基坑支護結構,坑底抗隆起安全系數不能小于Kb=1.8。因此,由表2可知,如基坑抗隆起安全系數需達到規范要求,圍護樁樁長插入深度至少需要達到深度ld=6.1 m。

圖1 不同樁長插入深度下的基坑抗隆起安全系數
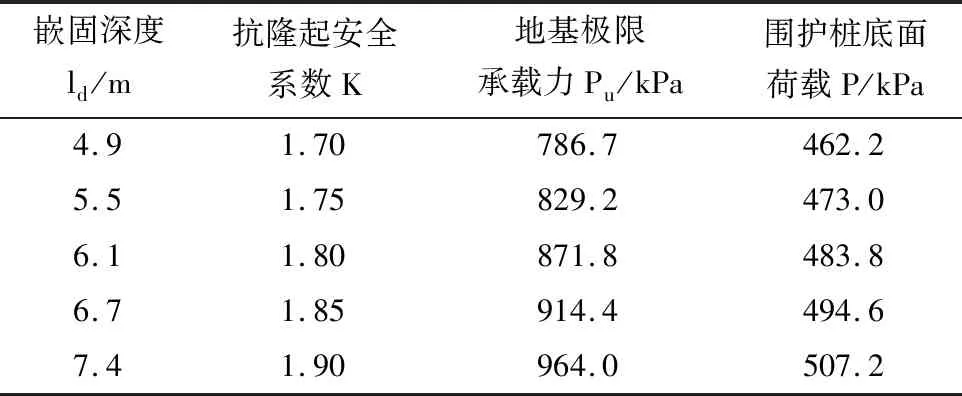
表2 抗隆起安全系數與樁長插入深度的關系
2.3 圍護樁嵌固深度的可靠度設計
假定c、φ、r1、r2、q0為相互獨立的正態隨機變量,各計算參數的均值分別為:c=15 kPa,φ=150,r1=22 kg/m3,r2=18 kg/m3,q0=50 kPa。由文獻[10]可知,土體黏聚力c變異系數大致為0.3~0.5;土體內摩擦角φ大致為0.1~0.4;土體重度r的變異系數較小,大致為0.02~0.08;地面荷載q0的變異系數這里假定為0.1~0.3。結合以上各變量參數變異性范圍,取三種變異系數分別進行分析。變異系數取值見下表所示。

表3 各土層參數變異程度分類
根據概率統計知識計算,得到了基坑坑底抗隆起穩定性可靠度指標與不同樁長插入深度的關系,結果詳見圖2及表4。由計算結果可知,基坑坑底抗隆起穩定性不僅與土層參數大小有關,同時受土層參數的變異性大小影響顯著。當土層參數的變異性越大,抗隆起穩定性越差,因此盡管安全系數能夠滿足要求,但仍不滿足可靠度指標的要求,此時,樁長插入深度需要加大。例如本工程工況,當圍護樁嵌固深度為5.03 m時,土層參數的不確定程度為δ(1)增時,可靠度指標為3.0,當不確定程度增加到δ(2)時,可靠度指標則減小至2.27;而當土層參數的不確定程度進一步加大至δ(3)時,可靠度指標則進一步減小至1.57。

圖2 抗隆起可靠度指標與錨固深度的關系

表4 不同嵌固深度下抗隆起可靠度指標與圍護樁樁長插入深度的關系
由文獻[10],當基坑安全等級為一級時,基坑坑底抗隆起穩定性的控制性可靠度指標可取3.0。由計算結果可知,當土層參數的不確定程度為δ(1)時,圍護樁樁長插入深度需設計至5.03 m時能夠滿足計算要求,此時安全系數K為1.71;當土層參數的不確定程度加大至δ(2)時,圍護樁嵌固深度ld=7.11 m時才能滿足設計要求,而此時根據確定性模型計算的安全系數K為1.88;當土層參數的不確定程度進一步加大至δ(3)時,圍護樁樁長插入深度需進一步加大至8.89 m才能滿足計算要求,而此時根據確定性模型計算的安全系數K為2.0。因此,當土層參數不確定程度加大時,需要加長圍護樁插入深度,以滿足計算要求。
綜上所述,當圍護樁嵌固深度ld=6.1 m時,基坑坑底抗隆起安全系數K=1.80,根據確定性計算模型,安全系數能夠滿足計算要求;而根據不確定性模型判斷,當土層參數的不確定程度較小取δ(1)時,計算結果大于可靠度控制指標,滿足計算要求;當土層參數的不確定性程度加大至δ(2)、δ(3)時,計算得到的可靠度指標均小于控制性可靠度指標,從而不能滿足計算。根據上述計算對比,對于土層較為均勻的地區,傳統的確定性模型計算得到的安全系數確定圍護樁樁長插入深度具有一定的安全儲備;當對于土層差異性加大的地區,土層參數的不確定性程度加大時,采用確定性模型進行設計時安全儲備不夠,需要考慮土層參數的不確定性程度,利用極限狀態設計的方法來確定圍護樁樁長。
2.4 各土層參數的不確定程度對可靠度指標的影響分析
根據計算結果可知,基坑坑底抗隆起穩定性均隨各土層參數的不確定程度的增加而減小。根據數據對比,參數φ的不確定性程度對基坑坑底抗隆起穩定性影響最大,土層參數c的不確定性程度對抗隆起穩定性的影響也較大,因此在設計時需重點考慮這兩個土層參數的不確定性程度;而土層參數r1、r2、q0的不確定程度對基坑坑底抗隆起穩定性的影響較小,可忽略不計。

表5 各土層參數的不確定程度與可靠度指標的關系
3 結 論
(1)對于此工程工況,采用傳統的確定性計算模型時,圍護樁插入深度需設計至6.1 m時能夠滿足安全系數計算要求;而當采用不確定性計算模型時,當土層參數的不確定性程度分別為δ(1)、δ(2)、δ(3)時,圍護樁插入深度需分別設計至為5.03 m、7.11 m、8.89 m能夠滿足可靠度指標計算要求。
(2)對于土層參數變化加大的地區,需要考慮土層參數的不確定性程度,利用極限狀態設計方法進行圍護樁插入深度計算,對于基坑坑底抗隆起穩定性的安全儲備性更高。
(3)利用可靠度指標去指導圍護樁嵌固深度設計時,需要特別注意土體內摩擦角φ、黏聚力c的變異性。

