高雷諾數低溫風洞內傳熱特性數值研究

高鑫宇，聶旭濤，蔡清青，張偉

高雷諾數低溫風洞內傳熱特性數值研究

高鑫宇，聶旭濤，蔡清青，張偉

（中國空氣動力研究與發展中心，四川 綿陽 621000）

低溫風洞的超音速及其高雷諾數工況下的換熱特性是分析低溫風洞組件溫度場分布的關鍵因素。對超音速及高雷諾數工況換熱特性進行數值模擬，通過采用恢復溫度修正傳熱系數的方法，并且與Dittus-Boleter（D-B）公式和Gnielinski公式的計算結果進行對比分析。結果顯示，采用恢復溫度修正后的D-B公式和Gnielinski公式在超音速及其高雷諾數工況下仍然具有較高準確性。最后將噴管段實際模型工況數值模擬結果與理論預測值進行對比分析，進一步驗證了在溫度分布不均勻時采用D-B公式和Gnielinski公式求得的平均換熱系數在工程計算中的可行性，以及使用恢復溫度修正傳熱系數計算公式的有效性。

低溫風洞；高雷諾數；超音速；換熱特性；恢復溫度

隨著空氣動力學的飛速發展，對作為試驗設備的風洞有了更高的要求。目前常規風洞已經無法完成雷諾數高于50×106的試驗要求，而低溫風洞[1]通過降低氣流溫度的方法達到提高風洞雷諾數模擬的目的，已經成為目前實現高雷諾數模擬的最佳方案。由于液氮在低溫工質中廉價和安全，汽化后可迅速吸收大量熱量從而噴射液氮，成為目前低溫風洞中實現風洞空氣回路快速降溫的主要途徑。目前，世界上兩座大型的跨聲速低溫風洞——美國國家跨聲速風洞（NTF）和歐洲跨聲速風洞（ETW）均采用液氮工質制冷實現低溫運行[2-3]。低溫風洞在運行過程中，低溫流體在風洞中快速流動，通過對流換熱與風洞中的結構建立熱平衡，從而實現低溫實驗條件，氣流溫度甚至最低可達到90 K[4]，在這樣低的氣流溫度下，整個風洞的雷諾數很高，可達到108量級，使得氣流與風洞的對流換熱劇烈，由于熱脹冷縮的作用，對風洞各部件的安全性和密封性提出了更高的要求。為保證風洞的安全運行，需要對風洞傳熱進行全面的計算分析，尤其是風洞處于高雷諾數和超音速時的換熱特性。

國內外對高速流動換熱特性進行了研究。文獻[5]在對高速噴管內部的對流換熱計算方法進行研究時，采用絕熱壁面溫度（恢復溫度）求解對流換熱系數。文獻[6]在進行高速平板邊界層的對流換熱研究時，引入了恢復溫度求解對流換熱系數。文獻[7]在研究收斂擴張噴管湍流邊界層的熱量測量方法時，引入了恢復溫度的概念。

本文采用Fluent軟件對高雷諾數及其超音速工況下的管內流動對流換熱進行研究，引入恢復溫度的概念進行對流換熱求解，并與管內對流換熱公式進行了對比驗證。此外，對風洞收縮噴管段模型換熱系數進行模擬求解，與管內流動強制對流換熱經驗公式進行對比分析。驗證了管內流動在引入恢復溫度修正后的可行性和準確性，并且驗證了D-B公式在雷諾數為107的量級也是適用的。

1 對流換熱系數的求解方法

對于管內流動對流換熱系數主要通過CFD數值模擬和經驗公式兩個方面進行求解。

1.1 CFD數值模擬

換熱系數的求解公式[8]如下：

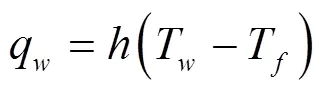
式中：q為對流換熱熱流密度，W/m2；T、T分別為物體表面和流體的溫度，K；為對流換熱系數，W/(m2·K)。

式（1）適用于低速流體，當流體速度很高時則要考慮粘性流體摩擦引起的溫升，即[9-10]：

式中：T為壁面恢復溫度，K；為恢復系數，其物理意義為絕熱壁面由摩擦而引起的溫升與高速氣體駐點的絕熱溫升之比；為流體比熱比，無量綱；∞為流體主流溫度，K；∞為流體主流流動馬赫數，Ma。

當∞為無窮小時T＝∞，高速流體的公式與低速流體的公式完全吻合。

層流時[6]，有：

湍流時[6]，有：

式中：為普朗特數。

用CFD數值模擬求解換熱系數，在給定恒定固體壁面溫度時，可通過CFD求解出流體與壁面的熱流密度，并通過式（3）求解出T，進而通過式（2）求解出換熱系數。

本文使用Fluent軟件進行CFD數值模擬，選用湍流模型、標準壁面函數，求解方式采用壓力基SIMPLE進行求解，流體物性采用NIST物性數據庫。

1.2 采用經驗公式求解換熱系數

根據相關研究[3]影響對流換熱系數的主要因素可定性地用函數形式表示為：

式中：為流體流動速度；、、、、c為幾何結構換熱表面的特征長度、密度、粘度、導熱系數和定壓比熱。

在低溫風洞中流體高速流動，主要涉及的換熱類型是管內流動強制對流換熱，而常用管內流動強制對流換熱經驗公式有Dittus-Boelter（D-B）公式和Gnielinski方程。

D-B方程[8]為：

式中：當流體被加熱時取0.4，當流體被冷卻時取0.3；＞10000。

該經驗公式一般要求≥10（其中：為流體管道直徑，m；為流體流動管長，m）。

當/＜10時，需要考率入口效應，工程上常采用的入口效應修正系數為[9]：

Gnielinski方程為：

其中：

從圖1可以看出D-B公式和Gnielinski公式在104～108范圍內整體吻合得很好，在106.5～108范圍，D-B公式的值較大，但目前兩個公式的實驗驗證范圍還沒有達到107～108量級。但當風洞處于高壓及高速流動甚至風速在實驗段達到超音速時，管內流動的雷諾數可以達到107～108這個量級。本文通過Fluent進行數值模擬分析并通過與常用管內流動經驗公式進行對比分析，給出一個可以預測風洞處于高雷諾數時強制對流換熱可應用的經驗公式。

2 數值模擬

為了驗證CFD數值模擬的正確性，本文通過外掠平板換熱系數結果進行驗證。本文在進行數值模擬過程中取板的特征長度為1 m，氮氣溫度為200 K，壓強為1 bar，平板溫度取恒定壁溫220 K，材料為不銹鋼。邊界條件為：進口采用速度進口，出口采用流量出口，平板采用恒定壁溫，無滑移，其余壁面采用絕熱，無滑移。圖2為流體外掠平板的溫度分布，可以看出平板表面的熱邊界層厚度逐漸增厚，這符合熱力學一般現象。

圖2 平板溫度分布

這里定性溫度按210 K取，物性參數采用NIST REFPROP數據庫。

從圖3可看出，Fluent仿真結果和解析解吻合得很好，并且誤差較小，因此可以采用CFD方法在給定恒定壁面溫度邊界條件，通過求解固體壁面和流體間換熱的熱流密度，從而對低溫流體求解換熱系數。

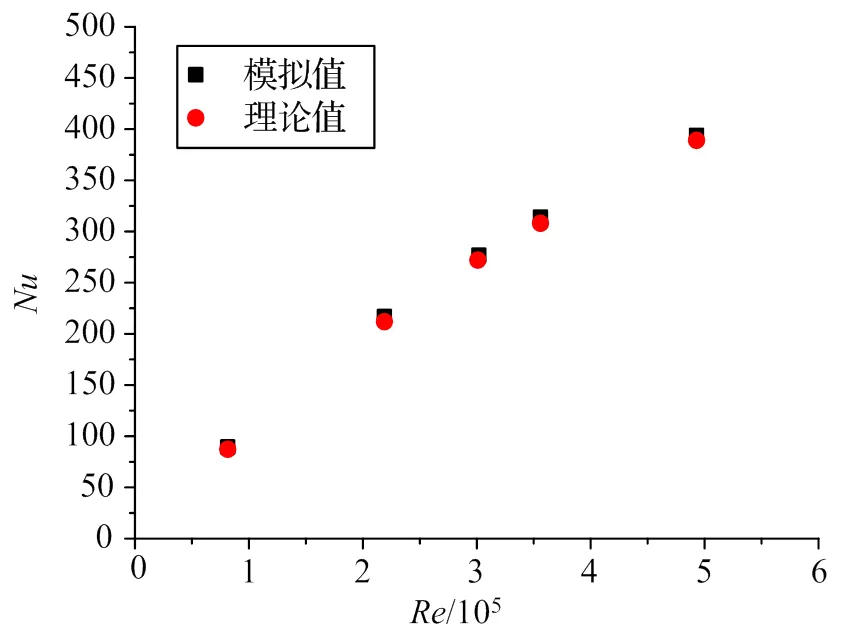
圖3 平板處于層流狀態時Nu模擬值和理論值對比

對于雷諾數＜500000，平板處于層流狀態，理論值根據如下經驗公式計算：

3 高雷諾數算例

選取管道直徑為1 m，管長為20 m，取馬赫數為0.1、0.2、0.4、0.6的四種工況進行驗證，流體溫度100 K，管壁溫度150 K，流體壓強為1 bar。邊界條件為進口采用壓力進口，出口采用壓力出口，壁面采用無滑移恒定壁面溫度。

經過計算，管內流動模擬值與理論值對比如圖4所示，其中CFD修正模擬值采用式（2）（3）即引入恢復溫度進行修正，此時雷諾數范圍在107量級。可以看出，模擬值與經驗公式計算值整體吻合得較好，尤其在低馬赫數時CFD未修正值和修正值差別不大、且均和D-B公式和Gnielinski公式吻合很好，這是由于低馬赫數時恢復溫度近似等于流體靜溫。而在高馬赫數，可以看出采用恢復溫度修正過后的CFD換熱系數模擬值與Gnielinski吻合很好，而未修正過的CFD模擬值與經驗公式計算值差值較大，說明D-B公式和Gnielinski公式可以應用于低溫風洞中的高雷諾數范圍進行工程計算，并且在采用CFD數值模擬進行求解換熱系數時在高馬赫數時需要用恢復溫度對換熱系數定義式進行修正。

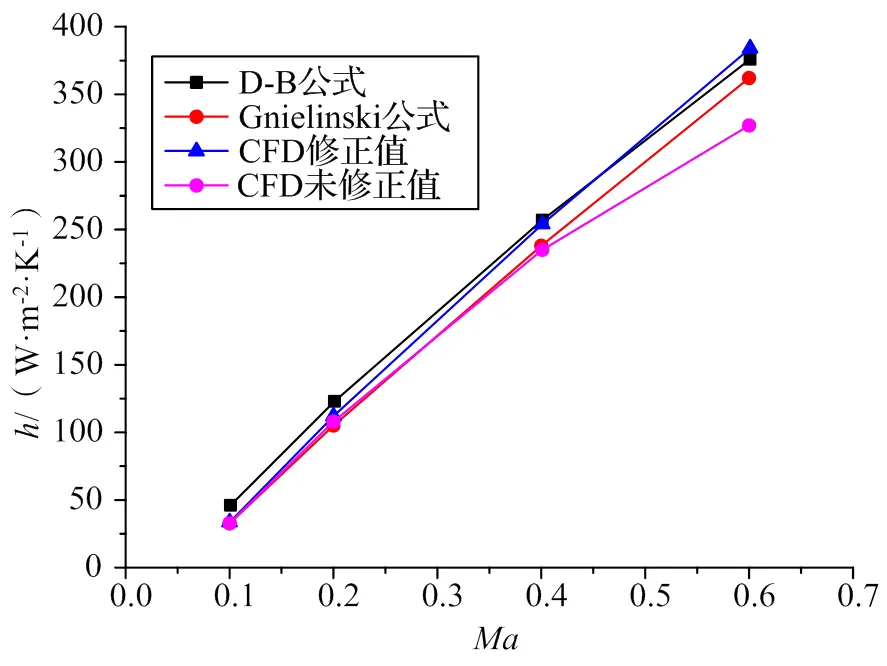
圖4 換熱系數CFD模擬值與經驗公式值對比

4 超音速等直徑管換熱

對超音速流速下的等直徑圓形管道進行CFD數值模擬，用Fluent求解超音速換熱時采用密度基瞬態求解，直到算到穩態，考慮氣體的可壓縮性，流體物性采用Refprop軟件擬合。考慮長徑比為10的等直徑管及長徑比為2的等直徑管，如表1所示。邊界條件為進口采用壓力進口，出口采用壓力出口，壁面采用無滑移恒定壁面溫度。

表1 等直徑管參數及其流體工況參數

4.1 算例1結果分析

由圖5可以看出，在0.3 m附近，即管長為直徑的3倍長度時，馬赫數有一個從超音速向亞音速的突變，出現管道堵塞現象[12]。即實際氣體在等直徑管中流動，等直徑管道相當于漸縮管，考慮摩擦作用時由超音速氣流不能連續轉變為亞音速氣流，出口的極限狀態只能為聲速。

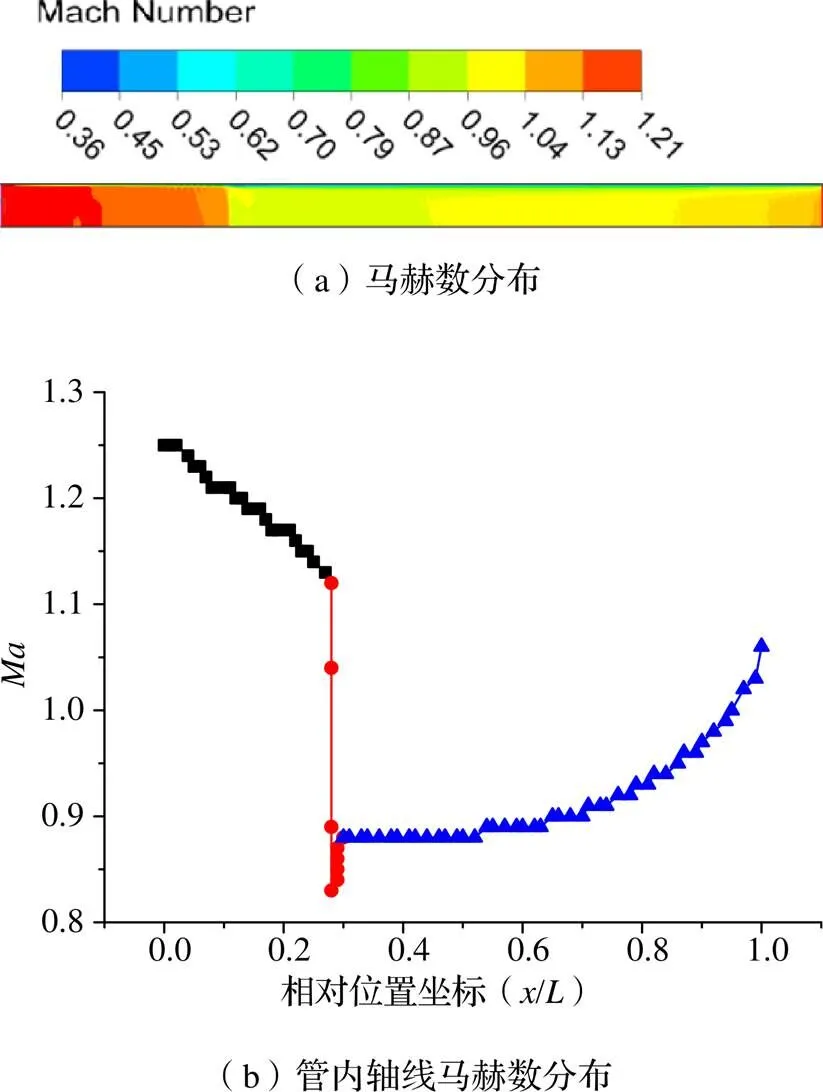
圖5 算例1的馬赫數分布

4.2 算例2結果分析

由圖6可以看出，管內超聲速的流動現象基本上是符合理論基礎的，即等直徑管內超聲速流動速度減小，但最小減小到跨音速，否則會出現堵塞現象[12]。整個管內的流動均在超音速范圍內，說明管長小于限制管長。

圖6 算例2的馬赫數分布

算例2中，取＝1 bar、＝100 K、＝1.21×108，通過式（2）（3）采用恢復溫度對處于超音速工況流體求解換熱系數的定義式進行修正求得(CFD)＝986 W/(m2·K)，通過式（4）和（8）求得(D-B)＝928 W/(m2·K)，通過式（8）～（10）求得(Gnielinski)＝940 W/(m2·K)。可以看出D-B經驗公式和Gnielinski公式與CFD修正后的仿真結果均吻合較好，且兩個公式計算結果在雷諾數在108這個量級的計算結果相差不大，可以說明D-B公式和Gnielinski公式在超音速高雷諾數的適用性。

5 收縮噴管段實際模型換熱分析

為進一步驗證D-B公式和Gnielinski公式在超音速高雷諾數下的適用性，對低溫風洞收縮噴管段實際模型針對靜溫變化比較大的工況進行CFD模擬。如圖7所示的風洞收縮噴管段結構模型，分為收縮段、硬板噴管段、柔板噴管段三個部分。

圖7 風洞收縮噴管段模型

氮氣實現跨音速流動，需要考慮工質壓縮性，使用壓力邊界條件，進口壓力為inlet,total＝3.5 bar，出口壓力為outlet,static＝1.263199 bar，出口馬赫數達到1.3。壁面邊界條件對于靜態流場分析，壁面采用恒壁溫邊界條件，壁面是氣動降溫過程，流體壁面溫度設置為比流體入口主流溫度高50 K。

計算結果如圖8所示，壓力沿流動方向逐漸減小，速度逐漸增大，在喉部位置氮氣流速達到音速，v＝194.05 m/s。噴管內氮氣壓力不斷降低，流速不斷增加，內腔體壁面換熱性能沿氣流方向不斷變化。

由圖9所示的換熱系數分布可以看出，縮放噴管換熱系數沿流動方向先增大后減小，頂部柔板的峰值在噴管喉部之前＝312 mm時最大值為1351.56 W/(m2·K)，側壁面的峰值也分布在喉部之前的位置，＝410 mm時最大值為1115.33 W/(m2·K)，有文獻[4]中研究發現CFD模擬值在喉部以前略小于實驗數據，在喉部以后與實驗數據吻合較好，且熱流密度的峰值在喉部以前。比較圖9（a）（b），可以看出本文模擬的噴管段換熱系數變化規律與文獻中的趨勢完全一致，且峰值的位置也一致，說明了模擬的正確性。

圖8 噴管流場仿真結果云圖

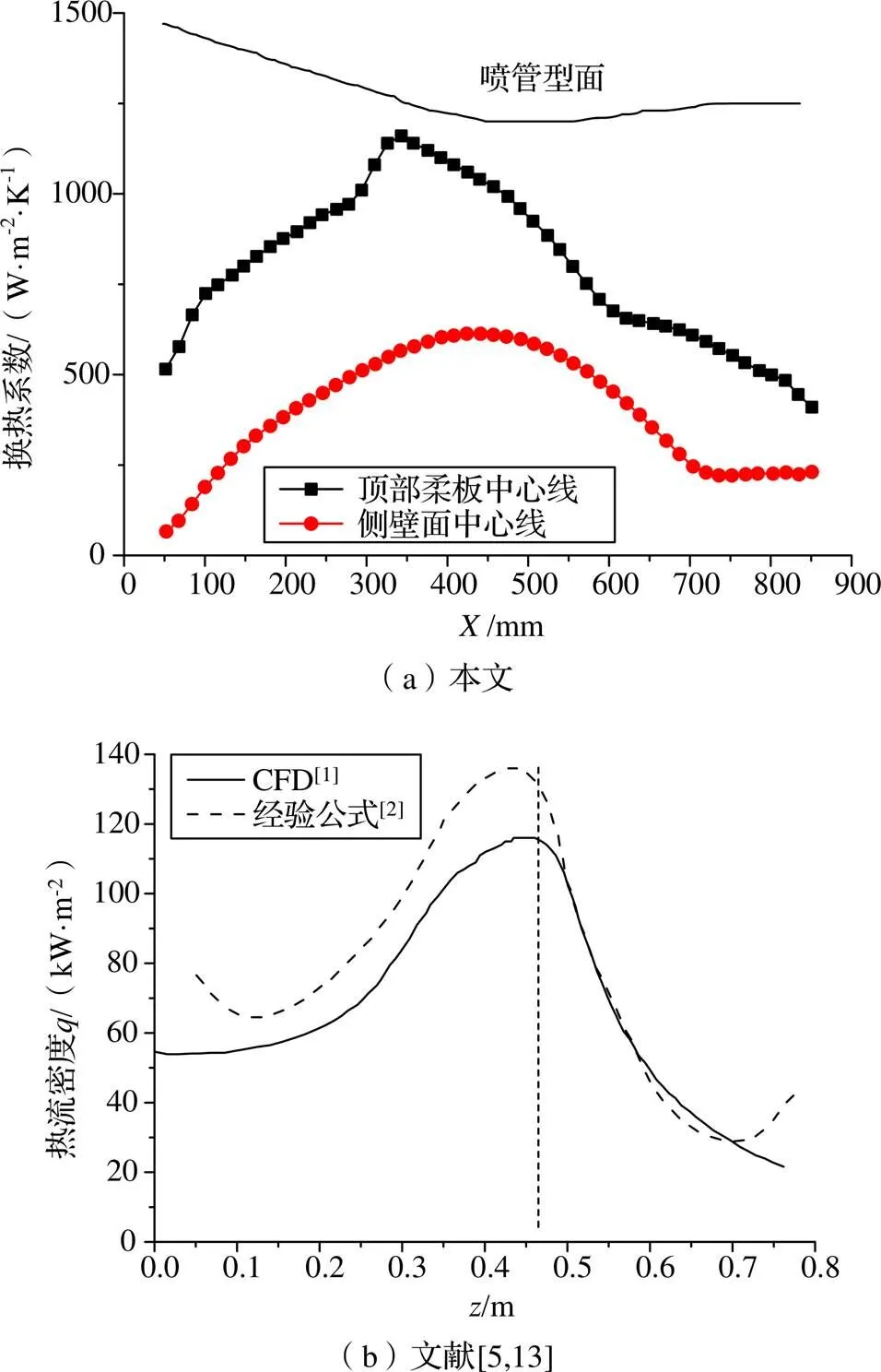
圖9 沿噴管型線換熱系數分布

使用經驗公式對噴管柔板處換熱系數進行工程計算，柔板段模型為縮放噴管，取平均當量直徑為d＝4A/＝0.2928 m。縮放噴管氣流速度始終增大，取當地音速v＝194.05 m/s作為平均速度，根據壓力分布云圖取柔板處壓力為1.988 bar，溫度取靜溫static＝94.184 K，計算物性根據工況條件通過NIST進行查找，計算結果如表2所示。

表2 流體物性參數

在＝194.05 m/s條件下求取噴管柔板處流道的面平均換熱系數，將數值分析值與經驗公式計算值進行對比，分析兩者誤差，驗證數值分析的準確性。對比結果如表3所示，考慮到速度、溫度、壓力均為變化數值，取平均值會引起誤差，則計算結果可靠。

表3 噴管柔板換熱系數對比結果

6 總結

通過對低溫流體超音速及其高雷諾數的換熱特性通過CFD和經驗公式對比分析，得出了在超音速及其高雷諾數工況，使用恢復溫度修正后的Dittus-Boelter公式和Gnielinski公式在高雷諾數時仍然具有實用性，并且兩個公式在雷諾數在108這個量級誤差很小，在106～108量級，Dittus-Boelter公式的計算結果偏大。

此外，本文對低溫風洞收縮噴管段實際模型進行了CFD仿真，與經驗公式的算例結果進行了對比分析，驗證了采用恢復溫度修正傳熱換熱系數定義公式進行CFD數值模擬計算換熱系數的科學性，以及兩個公式在高雷諾數范圍的工程適用性。

[1]Goodyer M J，Kilgore R A. High-Reynolds-Number Cryogenic Wind Tunnel[J]. Journal of the Japan Society for Aeronautical & Space Sciences，2013，42（480）：26-31.

[2]賴歡，陳振華，高榮，等. 大型高速低溫風洞冷量回收的方法研究[J]. 西安交通大學學報，2016，50（6）：136-142.

[3]劉政崇. 風洞結構設計（精）[M]. 北京：宇航出版社，2005.

[4]麻越垠，陳萬華，王元興，等. 基于ABAQUS的低溫風洞擴散段結構-熱耦合仿真研究[C].中國計算力學大會2014暨錢令希計算力學獎頒獎大會，2014.

[5]嚴慧芳，曾軍，婁德倉，等. 高速噴管內部對流換熱計算方法研究[J]. 航空科學技術，2015（10）：68-72.

[6]毛旭. 對流換熱邊界下高超音速平板邊界層相似性解研究[D]. 天津：天津大學，2013.

[7]Back L H，Massier P F，Gier H L. Convective heat transfer in a convergent-divergent nozzle[J]. International Journal of Heat and Mass Transfer，1964，7（5）：549-568.

[9]楊世銘，陶文銓. 傳熱學（BZ）（TB）[M]. 4版. 北京：高等教育出版社，2010.

[10]許鵬博，孫曉玲，章錦威，等. 高超聲速氣動加熱/結構傳熱耦合計算研究[C]. 全國計算流體力學會議，2014.

[11]李鵬飛，吳頌平. 類航天飛機前身結構與高超聲速流場的耦合傳熱模擬分析[J]. 航空動力學報，2010，25（8）：1705-1710.

[12]杜廣生. 工程流體力學[M]. 北京：中國電力出版社，2005.

[13]Stoll J，Straub J. Film cooling and heat transfer in nozzles[J]. Journal of turbo machinery，1988，110（1）：57-65.

[14]吳加俊，戴恒震. 基于ABAQUS的導電滑環的單絲靜態接觸力學特性分析[J]. 機械，2018，7（18）：18-22.

[15]文華，王玲，殷國富，等. 插裝閥集成塊內部流道流場分析研究[J]. 機械，2017，5（10）：10-13.

Numerical Study of Heat Transfer Characteristics in Cryogenic Wind Tunnel at High Reynolds Number

GAO Xinyu，NIE Xutao，CAI Qingqing，ZHANG Wei

(China Aerodynamics Research and Development Center, Mianyang 621000, China )

The heat transfer characteristics of cryogenic wind tunnel under supersonic and high Reynolds number conditions are the key factors to analyze the distribution of the temperature field in cryogenicwind tunnel. The heat transfer characteristics under supersonic and high Reynolds number conditions are simulated by using the recovery temperature correction heat transfer coefficient calculation method, and the results are compared with the calculations by Dittus-Boelter equation and Gnielinski equation. The results show that the application of D-B formula and Gnielinski equation under supersonic and high Reynolds number conditions after the recovery temperature correction still have a high validity. Finally, the numerical simulation results of the spray pipe section are compared with the predicated values and analyzed, which further verifies the applicability of the average heat transfer coefficient obtained by the above two equations and the validity of the recovery temperature correction heat transfer coefficient calculation formula with non-uniform temperature distribution.

cryogenic wind tunnel；high Reynolds number；supersonic；heat transfer characteristics；recovery temperature

TB69

A

10.3969/j.issn.1006-0316.2021.11.005

1006－0316 (2021) 11－0034－07

2021－01－22

高鑫宇（1985－），男，四川仁壽人，碩士，工程師，主要研究方向為風洞設備結構設計等，E-mail：gaokerry@126.com；聶旭濤（1979－），男，安徽宿松人，博士，副研究員，主要研究方向為風洞設備結構設計等。